Next: 3. Συντελεστές και σειρές Up: 2. Τριγωνομετρικά πολυώνυμα Previous: 2.5 Άρτιες και περιττές Contents Index
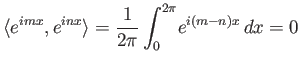
Υπόδειξη: Βρείτε, για κάθε
![]() , δύο διαφορετικά στοιχεία
, δύο διαφορετικά στοιχεία
![]() που να απέχουν το πολύ
που να απέχουν το πολύ ![]() . Τότε οι αριθμοί
. Τότε οι αριθμοί
![]() ,
,
![]() , ανήκουν στην
, ανήκουν στην ![]() .
.
Τέλος, δείξτε ότι η υποομάδα ![]() στην (2.11) είναι πυκνή στο
στην (2.11) είναι πυκνή στο
![]() .
.
Υπόδειξη: Το ότι ![]() είναι άρρητος συνεπάγεται ότι διαφορετικά
είναι άρρητος συνεπάγεται ότι διαφορετικά ![]() μας δίνουν
διαφορετικούς αριθμούς
μας δίνουν
διαφορετικούς αριθμούς
![]() . Δείξτε ότι η
. Δείξτε ότι η ![]() έχει σημείο συσσώρευσης δείχνοντας ότι έχει
άπειρα στοιχεία στο διάστημα
έχει σημείο συσσώρευσης δείχνοντας ότι έχει
άπειρα στοιχεία στο διάστημα ![]() .
.
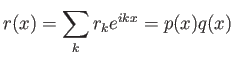
Mihalis Kolountzakis 2015-11-28