Next: 6.4 Σύγκλιση κατά Up: 6. Σύγκλιση των μερικών Previous: 6.2 Όχι σύγκλιση κατά Contents Index
Δείχνουμε τώρα ότι δεν ισχύει απαραίτητα ούτε
![]() για κάθε
για κάθε
![]() .
.
Πράγματι, αν ίσχυε κάτι τέτοιο, όπως και στην περίπτωση της σύγκλισης κατά ![]() , θα είχαμε ότι
για κάθε
, θα είχαμε ότι
για κάθε
![]() η ακολουθία
η ακολουθία
![]() είναι φραγμένη και άρα από το Θεώρημα Banach-Steinhaus
(Θεώρημα 6.2) θα υπήρχε
είναι φραγμένη και άρα από το Θεώρημα Banach-Steinhaus
(Θεώρημα 6.2) θα υπήρχε ![]() τ.ώ. να ισχύει
τ.ώ. να ισχύει
Επειδή όμως
![]() αυτό το κάτω φράγμα αντιφάσκει με την (6.3) αφού η ποσότητα
αυτό το κάτω φράγμα αντιφάσκει με την (6.3) αφού η ποσότητα ![]() μπορεί να γίνει οσοδήποτε μεγάλη.
μπορεί να γίνει οσοδήποτε μεγάλη.
Έστω
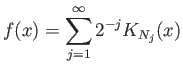
Υπόδειξη: Αν η ακολουθία ![]() αυξάνει αρκετά γρήγορα τότε για άπειρες τιμές του
αυξάνει αρκετά γρήγορα τότε για άπειρες τιμές του ![]() μπορούμε να πετύχουμε να υπάρχει ένας
μόνο από τους όρους
μπορούμε να πετύχουμε να υπάρχει ένας
μόνο από τους όρους