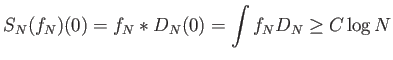6.2 Όχι σύγκλιση κατά 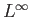
Η πρώτη περίπτωση που θα κοιτάξουμε είναι η περίπτωση που
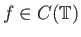 και η νόρμα
είναι η
και η νόρμα
είναι η
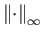 . Το ερώτημα, με άλλα λόγια, είναι αν η σειρά Fourier μιας συνεχούς
συνάρτησης συγκλίνει ομοιόμορφα στην συνάρτηση.
Γνωρίζοντας ότι δεν ισχύει
κατ' ανάγκη ούτε η κατά σημείο σύγκλιση, είναι φανερό ότι η απάντηση είναι όχι.
Αξίζει ίσως να επαναλάβουμε την απόδειξη χωρίς αναφορά στην κατά σημείο σύγκλιση.
. Το ερώτημα, με άλλα λόγια, είναι αν η σειρά Fourier μιας συνεχούς
συνάρτησης συγκλίνει ομοιόμορφα στην συνάρτηση.
Γνωρίζοντας ότι δεν ισχύει
κατ' ανάγκη ούτε η κατά σημείο σύγκλιση, είναι φανερό ότι η απάντηση είναι όχι.
Αξίζει ίσως να επαναλάβουμε την απόδειξη χωρίς αναφορά στην κατά σημείο σύγκλιση.
Πράγματι, αν υποθέσουμε ότι
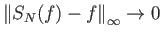 για κάθε
για κάθε
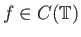 , τότε
οι τελεστές
, τότε
οι τελεστές
είναι φραγμένοι κατά σημείο, ισχύει δηλαδή για κάθε
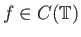 :
:
αφού ισχύει
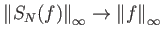 (αποδείξτε το αυτό).
Από το Θεώρημα Banach-Steinhaus (Θεώρημα 6.2) προκύπτει τότε
ότι οι τελεστές
(αποδείξτε το αυτό).
Από το Θεώρημα Banach-Steinhaus (Θεώρημα 6.2) προκύπτει τότε
ότι οι τελεστές 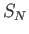 είναι ομοιόμορφα φραγμένοι, υπάρχει δηλ.
είναι ομοιόμορφα φραγμένοι, υπάρχει δηλ. 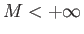 τ.ώ. να ισχύει
τ.ώ. να ισχύει
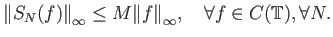 |
(6.2) |
Από το Πρόβλημα 6.3 όμως και το Λήμμα 6.1 προκύπτει
ότι για κάθε 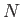 υπάρχει συνάρτηση
υπάρχει συνάρτηση
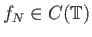 , με
, με
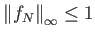 (μια συνεχής συνάρτηση που «προσεγγίζει»
τη συνάρτηση
(μια συνεχής συνάρτηση που «προσεγγίζει»
τη συνάρτηση
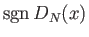 ), τ.ώ.
), τ.ώ.
όπου 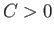 μια σταθερά (της οποίας η τιμή δεν έχει καμία σημασία για το πρόβλημα που εξετάζουμε).
Άρα
μια σταθερά (της οποίας η τιμή δεν έχει καμία σημασία για το πρόβλημα που εξετάζουμε).
Άρα
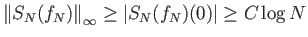 , το οποίο αντιφάσκει με την υπόθεση (6.2).
, το οποίο αντιφάσκει με την υπόθεση (6.2).
Άσκηση 6.4
Γιατί δεν εξετάζουμε καθόλου το ερώτημα αν συγκλίνει στην 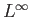 νόρμα
η ακολουθία
νόρμα
η ακολουθία 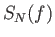 στην
στην 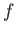 για κάθε
για κάθε
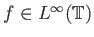 αλλά περιορίζουμε
αμέσως την
αλλά περιορίζουμε
αμέσως την 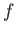 να είναι συνεχής;
να είναι συνεχής;
Mihalis Kolountzakis
2015-11-28
![]() και η νόρμα
είναι η
και η νόρμα
είναι η
![]() . Το ερώτημα, με άλλα λόγια, είναι αν η σειρά Fourier μιας συνεχούς
συνάρτησης συγκλίνει ομοιόμορφα στην συνάρτηση.
Γνωρίζοντας ότι δεν ισχύει
κατ' ανάγκη ούτε η κατά σημείο σύγκλιση, είναι φανερό ότι η απάντηση είναι όχι.
Αξίζει ίσως να επαναλάβουμε την απόδειξη χωρίς αναφορά στην κατά σημείο σύγκλιση.
. Το ερώτημα, με άλλα λόγια, είναι αν η σειρά Fourier μιας συνεχούς
συνάρτησης συγκλίνει ομοιόμορφα στην συνάρτηση.
Γνωρίζοντας ότι δεν ισχύει
κατ' ανάγκη ούτε η κατά σημείο σύγκλιση, είναι φανερό ότι η απάντηση είναι όχι.
Αξίζει ίσως να επαναλάβουμε την απόδειξη χωρίς αναφορά στην κατά σημείο σύγκλιση.
![]() για κάθε
για κάθε
![]() , τότε
οι τελεστές
, τότε
οι τελεστές