Next: 6.2 Όχι σύγκλιση κατά Up: 6. Σύγκλιση των μερικών Previous: 6. Σύγκλιση των μερικών Contents Index
Θα εξετάσουμε το ερώτημα του κατά πόσο μπορούμε να περιμένουμε τη σύγκλιση της σειράς Fourier
μιας συνάρτησης ![]() σε ένα σημείο
σε ένα σημείο ![]() στην τιμή
στην τιμή ![]() .
Φυσικά υπάρχουν περιπτώσεις όπου αυτό είναι εξασφαλισμένο, για παράδειγμα όταν
η συνάρτηση είναι συνεχής και
η σειρά συγκλίνει απόλυτα
.
Φυσικά υπάρχουν περιπτώσεις όπου αυτό είναι εξασφαλισμένο, για παράδειγμα όταν
η συνάρτηση είναι συνεχής και
η σειρά συγκλίνει απόλυτα
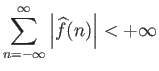
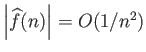 .
Όμως θα θέλαμε να εξετάσουμε το ερώτημα της κατά σημείο σύγκλισης με όσο το δυνατό λιγότερες προϋποθέσεις για τη
συνάρτηση
.
Όμως θα θέλαμε να εξετάσουμε το ερώτημα της κατά σημείο σύγκλισης με όσο το δυνατό λιγότερες προϋποθέσεις για τη
συνάρτηση
Το να υποθέσουμε μόνο ότι
![]() (η γενικότερη περίπτωση για την οποία μπορούμε να μιλάμε για
συντελεστές και σειρά Fourier) είναι πολύ λίγο, αφού δύο συναρτήσεις
(η γενικότερη περίπτωση για την οποία μπορούμε να μιλάμε για
συντελεστές και σειρά Fourier) είναι πολύ λίγο, αφού δύο συναρτήσεις
![]() οι οποίες διαφέρουν
σε ένα σύνολο μέτρου 0 έχουν την ίδια σειρά Fourier και δε μπορεί φυσικά αυτή η σειρά να συγκλίνει
και στο
οι οποίες διαφέρουν
σε ένα σύνολο μέτρου 0 έχουν την ίδια σειρά Fourier και δε μπορεί φυσικά αυτή η σειρά να συγκλίνει
και στο ![]() και στο
και στο ![]() , όταν το
, όταν το ![]() ανήκει σε αυτό το σύνολο μέτρου 0 στο οποίο οι
ανήκει σε αυτό το σύνολο μέτρου 0 στο οποίο οι ![]() και
και ![]() διαφέρουν.
Θα πρέπει λοιπόν η τιμή της συνάρτησης σε ένα οποιοδήποτε σημείο να είναι συνάρτηση των συντελεστών Fourier
της συνάρτησης και ο γενικότερος φυσιολογικός χώρος όπου αυτό ισχύει (από το θεώρημα της μοναδικότητας) είναι ο χώρος
διαφέρουν.
Θα πρέπει λοιπόν η τιμή της συνάρτησης σε ένα οποιοδήποτε σημείο να είναι συνάρτηση των συντελεστών Fourier
της συνάρτησης και ο γενικότερος φυσιολογικός χώρος όπου αυτό ισχύει (από το θεώρημα της μοναδικότητας) είναι ο χώρος
![]() των συνεχών
των συνεχών ![]() -περιοδικών συναρτήσεων.
-περιοδικών συναρτήσεων.
Έστω λοιπόν
![]() και
και
![]() . Ισχύει αναγκαστικά ότι
. Ισχύει αναγκαστικά ότι
![]() για
για
![]() ;
Η απάντηση είναι αρνητική.
;
Η απάντηση είναι αρνητική.
Θα δούμε ότι αυτό είναι συνέπεια ουσιαστικά του γεγονότος ότι ο πυρήνας του
Dirichlet ![]() δεν έχει φραγμένη
δεν έχει φραγμένη ![]() -νόρμα (για
-νόρμα (για
![]() ).
).
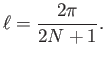
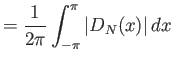 |
||
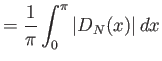 |
||
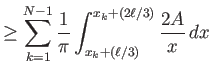 |
||
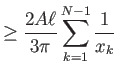 |
||
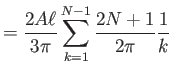 |
||
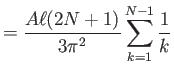 |
||
Γιατί όμως το Λήμμα 6.1 έχει ως συνέπεια, όπως προαναφέραμε, τη μη αναγκαστική σύγκλιση της
σειράς Fourier;
Κάνουμε κατ' αρχήν, για απλότητα, την επιλογή ![]() , και έπειτα
παρατηρούμε ότι η απεικόνιση
, και έπειτα
παρατηρούμε ότι η απεικόνιση
Οι δύο χώροι
![]() και
και
![]() είναι εφοαδιασμένοι με μετρική (νόρμα) την
είναι εφοαδιασμένοι με μετρική (νόρμα) την ![]() μετρική για τον πρώτο
και τη συνηθισμένη Ευκλείδια μετρική (απόλυτη τιμή) για το μιγαδικό επίπεδο.
Εύκολα προκύπτει ότι ένα γραμμικό συναρτησοειδές
μετρική για τον πρώτο
και τη συνηθισμένη Ευκλείδια μετρική (απόλυτη τιμή) για το μιγαδικό επίπεδο.
Εύκολα προκύπτει ότι ένα γραμμικό συναρτησοειδές ![]() είναι συνεχής συνάρτηση (ως προς τις δύο μετρικές) αν και μόνο
αν είναι συνεχής στο 0, το οποίο συμβαίνει αν και μόνο αν αυτό είναι φραγμένο, ισχύει δηλ. για κάποια πεπερασμένη
σταθερά
είναι συνεχής συνάρτηση (ως προς τις δύο μετρικές) αν και μόνο
αν είναι συνεχής στο 0, το οποίο συμβαίνει αν και μόνο αν αυτό είναι φραγμένο, ισχύει δηλ. για κάποια πεπερασμένη
σταθερά ![]() η ανισότητα
η ανισότητα
Κάθε νόρμα ορίζει μια μετρική στο χώρο ![]() , τη μετρική
, τη μετρική
![]() (η τριγωνική ανισότητα για την
(η τριγωνική ανισότητα για την ![]() είναι στην ουσία το 2 στις ιδιότητες της νόρμας παραπάνω).
είναι στην ουσία το 2 στις ιδιότητες της νόρμας παραπάνω).
Για ένα φραγμένο γραμμικό συναρτησοειδές ![]() το infimum των αριθμών
το infimum των αριθμών ![]() για τους οποίους
ισχύει η παραπάνω ανισότητα συμβολίζεται με
για τους οποίους
ισχύει η παραπάνω ανισότητα συμβολίζεται με
![]() και ονομάζεται νόρμα του γραμμικού
συναρτησοειδούς (και μπορούμε στη θέση του
και ονομάζεται νόρμα του γραμμικού
συναρτησοειδούς (και μπορούμε στη θέση του ![]() στην παραπάνω ανισότητα να πάρουμε τη νόρμα
στην παραπάνω ανισότητα να πάρουμε τη νόρμα
![]() ). Το σύνολο των φραγμένων γραμμικών συναρτησοειδών πάνω σε ένα χώρο με νόρμα, όπως
ο
). Το σύνολο των φραγμένων γραμμικών συναρτησοειδών πάνω σε ένα χώρο με νόρμα, όπως
ο
![]() που εξετάζουμε εδώ, είναι γραμμικός χώρος και η ποσότητα
που εξετάζουμε εδώ, είναι γραμμικός χώρος και η ποσότητα
![]() είναι μια νόρμα
πάνω στο γραμμικό αυτό χώρο.
Άρα η ποσότητα
είναι μια νόρμα
πάνω στο γραμμικό αυτό χώρο.
Άρα η ποσότητα
![]() είναι μια μετρική πάνω στο χώρο των συναρτησοειδών.
είναι μια μετρική πάνω στο χώρο των συναρτησοειδών.
Το πολύ σημαντικό θεώρημα που θα χρησιμοποιήσουμε για να δείξουμε τη μη (αναγκαστική) σύγκλιση
των ![]() στο
στο ![]() όταν η μόνη υπόθεση για την
όταν η μόνη υπόθεση για την ![]() είναι ότι
είναι ότι
![]() ,
είναι το Θεώρημα Banach-Steinhaus ή Αρχή Ομοιόμορφου Φράγματος, το οποίο διατυπώνουμε
εδώ μόνο για τους χώρους που μας ενδιαφέρει.
Για την απόδειξη παραπέμπουμε σε οποιοδήποτε καλό βιβλίο Συναρτησιακής Ανάλυσης.
,
είναι το Θεώρημα Banach-Steinhaus ή Αρχή Ομοιόμορφου Φράγματος, το οποίο διατυπώνουμε
εδώ μόνο για τους χώρους που μας ενδιαφέρει.
Για την απόδειξη παραπέμπουμε σε οποιοδήποτε καλό βιβλίο Συναρτησιακής Ανάλυσης.
Το ίδιο ισχύει και αν το πεδίο τιμών των ![]() δεν είναι οι πραγματικοί ή μιγαδικοί αριθμοί
αλλα οποιοσδήποτε γραμμικός χώρος με νόρμα
δεν είναι οι πραγματικοί ή μιγαδικοί αριθμοί
αλλα οποιοσδήποτε γραμμικός χώρος με νόρμα ![]() , και το πεδίο ορισμού των
, και το πεδίο ορισμού των ![]() είναι οποιοσδήποτε
πλήρης γραμμικός χώρος με νόρμα
είναι οποιοσδήποτε
πλήρης γραμμικός χώρος με νόρμα ![]() (ένας χώρος Banach όπως λέμε): αν για κάθε
(ένας χώρος Banach όπως λέμε): αν για κάθε ![]() ισχύει
ισχύει
Αν
![]() τότε είναι φανερό ότι
τότε είναι φανερό ότι
Απομένει λοιπόν να δείξουμε ότι οι νόρμες των ![]() δεν είναι φραγμένες.
Θυμόμαστε τώρα ότι
δεν είναι φραγμένες.
Θυμόμαστε τώρα ότι
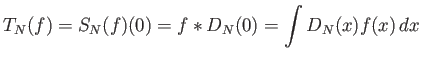
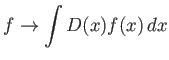
Υπόδειξη: Η ανισότητα
![]() έπεται από την προφανή ανισότητα
έπεται από την προφανή ανισότητα
![]() . Απομένει να δείξει κανείς ότι ισχύει
. Απομένει να δείξει κανείς ότι ισχύει
![]() για κάθε
για κάθε
![]() και για κάποια
συνεχή
και για κάποια
συνεχή ![]() με
με
![]() . Αν μπορούσαμε να πάρουμε
. Αν μπορούσαμε να πάρουμε
![]() (
(
![]() είναι
είναι ![]() αν
αν ![]() .
.![]() αν
αν ![]() και 0 αν
και 0 αν ![]() ) θα είχαμε την
ανισότητα αυτή ακόμη και με
) θα είχαμε την
ανισότητα αυτή ακόμη και με
![]() αλλά μια τέτοια συνάρτηση είναι ασυνεχής εν γένει
και άρα δεν είναι επιτρεπτή στον έλεγχο της νόρμας του συναρτησοειδούς. Μπορούμε
όμως να προσεγγίσουμε τη συνάρτηση αυτή με μια συνεχή συνάρτηση φραγμένη από το 1 με
τρόπο ώστε να μην επηρεάζουμε το ολοκλήρωμα
αλλά μια τέτοια συνάρτηση είναι ασυνεχής εν γένει
και άρα δεν είναι επιτρεπτή στον έλεγχο της νόρμας του συναρτησοειδούς. Μπορούμε
όμως να προσεγγίσουμε τη συνάρτηση αυτή με μια συνεχή συνάρτηση φραγμένη από το 1 με
τρόπο ώστε να μην επηρεάζουμε το ολοκλήρωμα ![]() παρά ελάχιστα.
παρά ελάχιστα.
Η απόδειξη του Θεωρήματος 6.1 είναι πλήρης με το Πρόβλημα 6.3.
Θα ασχοληθούμε τώρα με το κατά πόσον
Mihalis Kolountzakis 2015-11-28