Next: 6. Σύγκλιση των μερικών Up: 5. Η θεωρία Previous: 5.2 Εφαρμογή: Η ισοπεριμετρική Contents Index
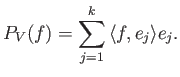
Κάτι άλλο που οφείλουμε να πούμε εδώ είναι ότι κάθε γραμμικός χώρος (πάνω στον οποίο έχουμε ορίσει
κάποιο εσωτερικό γινόμενο (ώστε να έχει νόημα να μιλάμε για ορθογωνιότητα) έχει κάποια ορθοκανονική
βάση
![]() όπου
όπου
![]() . Αυτό είναι εύκολο να δειχτεί επαγωγικά ως προς τη διάσταση
. Αυτό είναι εύκολο να δειχτεί επαγωγικά ως προς τη διάσταση
![]() και μπορεί επίσης να αποδειχτεί με χρήση της λεγόμενης ορθοκανονικοποίησης Gram-Schmidt
την οποία θα δούμε παρακάτω.
και μπορεί επίσης να αποδειχτεί με χρήση της λεγόμενης ορθοκανονικοποίησης Gram-Schmidt
την οποία θα δούμε παρακάτω.
Υπόδειξη: Αν υπάρχει και άλλο τέτοιο διάνυσμα ![]() τότε το τρίγωνο
τότε το τρίγωνο ![]() έχει ορθή γωνία
και στην κορυφή
έχει ορθή γωνία
και στην κορυφή ![]() και στην κορυφή
και στην κορυφή ![]() . Δείξτε ότι αυτό είναι αδύνατο εφαρμόζοντας δύο φορές
το Πυθαγόρειο θεώρημα. Με άλλα λόγια η υποτείνουσα είναι πάντα η αυστηρά μεγαλύτερη πλευρά σε ένα
ορθογώνιο τρίγωνο και άρα δε μπορεί να υπάρχουν δύο υποτείνουσες.
. Δείξτε ότι αυτό είναι αδύνατο εφαρμόζοντας δύο φορές
το Πυθαγόρειο θεώρημα. Με άλλα λόγια η υποτείνουσα είναι πάντα η αυστηρά μεγαλύτερη πλευρά σε ένα
ορθογώνιο τρίγωνο και άρα δε μπορεί να υπάρχουν δύο υποτείνουσες.
Υπόδειξη: Κανονικοποιήστε τα ![]() .
.
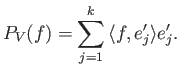
Υπόδειξη:
![]() για κάποια
για κάποια
![]() αφού τα
αφού τα ![]() παράγουν το
παράγουν το ![]() .
Παίρνοντας εσωτερικό γινόμενο αυτής της ισότητας με τα
.
Παίρνοντας εσωτερικό γινόμενο αυτής της ισότητας με τα ![]() παίρνετε το ζητούμενο.
παίρνετε το ζητούμενο.
Το επόμενο αποτέλεσμα είναι πολύ σημαντικό για την Ανάλυση.
Όπως είδαμε και στο Θεώρημα 5.4 το να μπορεί κανείς να υπολογίσει την ορθογώνια
προβολή ενός διανύσματος ![]() σε ένα γραμμικό χώρο
σε ένα γραμμικό χώρο ![]() ισοδυναμεί με το να βρεί το πλησιέστερο
διάνυσμα από το χώρο
ισοδυναμεί με το να βρεί το πλησιέστερο
διάνυσμα από το χώρο ![]() στο διάνυσμα
στο διάνυσμα ![]() .
Το αποδείξαμε αυτό στο Θεώρημα 5.4. Εκεί η απόδειξη
έγινε για ένα συγκεκριμένο διανυσματικό χώρο και εσωτερικό γινόμενο αλλά ισχύει σε οποιαδήποτε
περίπτωση. Και το να υπολογίσουμε την ορθογώνια προβολή του
.
Το αποδείξαμε αυτό στο Θεώρημα 5.4. Εκεί η απόδειξη
έγινε για ένα συγκεκριμένο διανυσματικό χώρο και εσωτερικό γινόμενο αλλά ισχύει σε οποιαδήποτε
περίπτωση. Και το να υπολογίσουμε την ορθογώνια προβολή του ![]() αν διαθέτουμε ήδη μια
ορθοκανονική βάση
αν διαθέτουμε ήδη μια
ορθοκανονική βάση
![]() του
του ![]() είναι πολύ εύκολο και δίνεται από
τον Ορισμό 5.3.
είναι πολύ εύκολο και δίνεται από
τον Ορισμό 5.3.
Οι περισσότεροι γραμμικοί χώροι που μας απασχολούν εδώ είναι φυσικά χώροι συναρτήσεων και τα διανύσματα είναι συναρτήσεις, αλλά δε χάνουμε τίποτε με το να την κρύψουμε αυτή την πληροφορία σε αυτή τη φάση, μια και το είδος διανυσμάτων για το οποίο μιλάμε δεν ενδιαφέρει (ακόμη) αλλά μόνο το ότι μπορούμε αυτά να τα προσθέτουμε μεταξύ τους και να τα πολλαπλασιάζουμε με αριθμούς παραμένοντας στον ίδιο χώρο. Αυτό που χρειαζόμαστε τώρα, μέχρι να αρχίσουμε να μιλάμε για χώρους πολυωνύμων, είναι ακριβώς αυτή η γραμμική δομή και το εσωτερικό γινόμενο που θεωρούμε ότι υπάρχει ορισμένο στο γραμμικό μας χώρο.
Είναι λοιπόν πολύτιμο το να έχουμε μια ορθοκανονική βάση του ![]() .
Αυτό το επιτυγχάνει κανείς με μια αλγοριθμική διαδικασία, τη λεγόμενη
ορθοκανονικοποίηση Gram-Schmidt.
.
Αυτό το επιτυγχάνει κανείς με μια αλγοριθμική διαδικασία, τη λεγόμενη
ορθοκανονικοποίηση Gram-Schmidt.
Η διαδικασία αυτή παίρνει ως είσοδο μια ακολουθία
![]() από γραμμικώς
ανεξάρτητα διανύσματα σε κάποιο γραμμικό χώρο
από γραμμικώς
ανεξάρτητα διανύσματα σε κάποιο γραμμικό χώρο ![]() (ο χώρος
(ο χώρος ![]() μπορεί να είναι και απειροδιάστατος
και η ακολουθία
μπορεί να είναι και απειροδιάστατος
και η ακολουθία ![]() μπορεί και να είναι μια άπειρη ακολουθία διανυσμάτων).
Η διαδικασία παράγει μια άλλη ορθοκανονική ακολουθία
μπορεί και να είναι μια άπειρη ακολουθία διανυσμάτων).
Η διαδικασία παράγει μια άλλη ορθοκανονική ακολουθία
![]() .
.
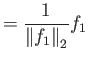 |
|||
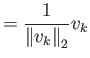 |
Το ότι η νόρμα των ![]() είναι 1 είναι άμεσο από τον ορισμό.
είναι 1 είναι άμεσο από τον ορισμό.
Αποδεικνύουμε με επαγωγή ως προς ![]() ότι τα διανύσματα
ότι τα διανύσματα
![]() είναι ορθοκανονικά
και παράγουν τον ίδιο χώρο με τα
είναι ορθοκανονικά
και παράγουν τον ίδιο χώρο με τα
![]() . Αυτό είναι προφανές για
. Αυτό είναι προφανές για ![]() αφού
το
αφού
το ![]() είναι πολλαπλάσιο του
είναι πολλαπλάσιο του ![]() .
Αν υποθέσουμε ότι ισχύει η πρόταση για το
.
Αν υποθέσουμε ότι ισχύει η πρόταση για το ![]() αποδεικνύουμε κατ' αρχήν ότι το
αποδεικνύουμε κατ' αρχήν ότι το ![]() είναι κάθετο
προς τα
είναι κάθετο
προς τα
![]() . Αυτό είναι φανερό μια και το
. Αυτό είναι φανερό μια και το ![]() ισούται με το
ισούται με το ![]() μείον την προβολή του στο χώρο
μείον την προβολή του στο χώρο
![]() και άρα (Πρόβλημα 5.14) είναι κάθετο σε ολόκληρο το χώρο
και άρα (Πρόβλημα 5.14) είναι κάθετο σε ολόκληρο το χώρο
![]() και άρα και στα ίδια τα
και άρα και στα ίδια τα
![]() .
Το διάνυσμα
.
Το διάνυσμα ![]() είναι απλά η κανονικοποίηση του
είναι απλά η κανονικοποίηση του ![]() και άρα είναι κι αυτό ορθογώνιο
στα
και άρα είναι κι αυτό ορθογώνιο
στα
![]() . Τέλος, αφού
. Τέλος, αφού
Κατά κάποιο τρόπο η διαδικασία Gram-Schmidt εξετάζει τα στοιχεία ![]() ένα προς ένα
και κρατάει από κάθε
ένα προς ένα
και κρατάει από κάθε ![]() το «κομμάτι» του που είναι ορθογώνιο με
το «κομμάτι» του που είναι ορθογώνιο με ![]() που έχουν υπολογιστεί μέχρι εκείνη τη στιγμή, δηλ. τα
που έχουν υπολογιστεί μέχρι εκείνη τη στιγμή, δηλ. τα
![]() .
Είναι σημαντικό να τονίσουμε ότι στον ορισμό του
.
Είναι σημαντικό να τονίσουμε ότι στον ορισμό του ![]() μέσω του βοηθητικού διανύσματος
μέσω του βοηθητικού διανύσματος ![]() (που είναι ουσιαστικά το
(που είναι ουσιαστικά το ![]() πριν κανονικοποιηθεί) όλα τα στοιχεία που εμφανίζονται στο
δεξί μέλος έχουν ήδη υπολογιστεί στα προηγούμενα στάδια της διαδικασίας και άρα γνωρίζουμε
ό,τι χρειάζεται για τον υπολογισμό.
πριν κανονικοποιηθεί) όλα τα στοιχεία που εμφανίζονται στο
δεξί μέλος έχουν ήδη υπολογιστεί στα προηγούμενα στάδια της διαδικασίας και άρα γνωρίζουμε
ό,τι χρειάζεται για τον υπολογισμό.
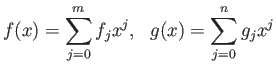
Με δεδομένη την τεράστια σημασία που έχουν οι χώροι πολυωνύμων
![]() στη θεωρία προσέγγισης καταλαβαίνει εύκολα κανείς πόσο σημαντικό είναι το ακόλουθο
αποτέλεσμα που μας δίνει ένα απλό ρόπο να
βρούμε μια ορθογώνια ακολουθία από μονικά πολυώνυμα όλων των βαθμών.
στη θεωρία προσέγγισης καταλαβαίνει εύκολα κανείς πόσο σημαντικό είναι το ακόλουθο
αποτέλεσμα που μας δίνει ένα απλό ρόπο να
βρούμε μια ορθογώνια ακολουθία από μονικά πολυώνυμα όλων των βαθμών.
Υποθέτουμε στα παρακάτω ότι έχουμε σταθεροποιήσει ένα κλειστό και φραγμένο διάστημα
![]() και μια θετική συνάρτηση βάρους
και μια θετική συνάρτηση βάρους ![]() πάνω στο διάστημα αυτό,
μέσω της οποίας ορίζεται ένα εσωτερικό γινόμενο
πάνω στο διάστημα αυτό,
μέσω της οποίας ορίζεται ένα εσωτερικό γινόμενο
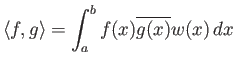
Αποδεικνύουμε την ορθογωνιότητα των
![]() με επαγωγή ως προς
με επαγωγή ως προς ![]() .
Για
.
Για ![]() αυτό είναι το αντικείμενο του Προβλήματος 5.24.
Αν υποθέσουμε ότι τα
αυτό είναι το αντικείμενο του Προβλήματος 5.24.
Αν υποθέσουμε ότι τα
![]() είναι ανά δύο ορθογώνια πρέπει,
για να ολοκληρώσουμε την επαγωγική απόδειξη, να δείξουμε ότι το
είναι ανά δύο ορθογώνια πρέπει,
για να ολοκληρώσουμε την επαγωγική απόδειξη, να δείξουμε ότι το ![]() είναι ορθογώνιο προς τα
είναι ορθογώνιο προς τα
![]() .
Δείχνουμε λοιπόν ότι
.
Δείχνουμε λοιπόν ότι
![]() για
για ![]() διαχωρίζοντας 3 περιπτώσεις για το
διαχωρίζοντας 3 περιπτώσεις για το ![]() .
.
Περίπτωση ![]() :
:
Χρησιμοποιώντας τον ορισμό του ![]() και το γεγονός (επαγωγική ως προς
και το γεγονός (επαγωγική ως προς ![]() υπόθεση)
ότι
υπόθεση)
ότι
![]() έχουμε
έχουμε
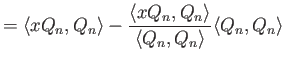 |
||
Περίπτωση ![]() :
:
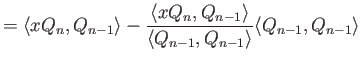 |
||
Περίπτωση ![]() :
:
Η απόδειξη του Θεωρηματος 5.6 είναι πλήρης.
Θα δείξουμε το ακόλουθο σημαντικό αποτέλεσμα το οποίο αργότερα θα εφαρμόσουμε σε μεθόδους αριθμητικής ολοκλήρωσης.
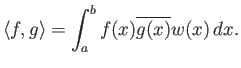
Το Θεώρημα 5.7 είναι άμεση συνέπεια του παρακάτω Λήμματος.
Για να αποδείξουμε το Λήμμα 5.2 θα χρειαστούμε την παρακάτω πρόταση.
Είναι πολύ εύκολο να βρει κανείς μια συνάρτηση
Έστω λοιπόν ![]() μια συνάρτηση τ.ώ.
μια συνάρτηση τ.ώ.
![]() και
και
![]() για
για
![]() .
Θα δείξουμε ότι ικανοποιεί και τις άλλες συνοριακές συνθήκες
.
Θα δείξουμε ότι ικανοποιεί και τις άλλες συνοριακές συνθήκες
![]() για
για
![]() .
.
Θα χρειαστούμε τον παρακάτω τύπο που γενικεύει τον τύπο ολοκλήρωσης κατά μέρη:
Αν τώρα
![]() τότε χρησιμοποιώντας τον τύπο (5.13)
και το ότι
τότε χρησιμοποιώντας τον τύπο (5.13)
και το ότι
![]() έχουμε
έχουμε
Για να είναι λοιπόν το αριστερό μέλος της (5.14) ίσο με 0 για κάθε
![]() ο μόνος τρόπος είναι να είναι όλοι οι συντελεστές
ο μόνος τρόπος είναι να είναι όλοι οι συντελεστές
![]() για
για
![]() . Με άλλα λόγια
πρέπει και αρκεί
. Με άλλα λόγια
πρέπει και αρκεί
![]() για
για
![]() , και η απόδειξη του Λήμματος 5.3
είναι πλήρης.
, και η απόδειξη του Λήμματος 5.3
είναι πλήρης.
Επανερχόμαστε τώρα στην απόδειξη του Λήμματος 5.2. Ας είναι
![]() ορθογώνια προς
το
ορθογώνια προς
το
![]() (δηλ. ορθογώνιο προς όλες τα στοιχεία του
(δηλ. ορθογώνιο προς όλες τα στοιχεία του
![]() ).
Από το Λήμμα 5.3 έχουμε ότι υπάρχει συνάρτηση
).
Από το Λήμμα 5.3 έχουμε ότι υπάρχει συνάρτηση
![]() τ.ώ.
τ.ώ.
![]() και όλες οι παράγωγοι της
και όλες οι παράγωγοι της ![]() τάξης μικρότερης του
τάξης μικρότερης του ![]() μηδενίζονται στα άκρα του διαστήματος.
Αφού
μηδενίζονται στα άκρα του διαστήματος.
Αφού ![]() από το θεώρημα του Rolle έχουμε ότι η
από το θεώρημα του Rolle έχουμε ότι η ![]() έχει κάποια ρίζα στο διάστημα
έχει κάποια ρίζα στο διάστημα ![]() .
Αφού η
.
Αφού η ![]() μηδενίζεται στα δύο άκρα και σε ένα ενδιάμεσο σημείο προκύπτει, και πάλι από το θεώρημα του
Rolle ότι η
μηδενίζεται στα δύο άκρα και σε ένα ενδιάμεσο σημείο προκύπτει, και πάλι από το θεώρημα του
Rolle ότι η ![]() έχει δύο διαφορετικές ρίζες στο
έχει δύο διαφορετικές ρίζες στο ![]() . Συνεχίζοντας κατ' αυτόν τον τρόπο,
εφαρμόζοντας δηλ. συνεχώς το θεώρημα του Rolle ώστε να «κερδίζουμε» από μια επιπλέον ρίζα
κάθε φορά που ανεβάζουμε την τάξη της παραγώγου της
. Συνεχίζοντας κατ' αυτόν τον τρόπο,
εφαρμόζοντας δηλ. συνεχώς το θεώρημα του Rolle ώστε να «κερδίζουμε» από μια επιπλέον ρίζα
κάθε φορά που ανεβάζουμε την τάξη της παραγώγου της ![]() , καταλήγουμε τελικά ότι η
, καταλήγουμε τελικά ότι η ![]() έχει
έχει
![]() διαφορετικές ρίζες στο
διαφορετικές ρίζες στο ![]() . Η απόδειξη του Λήμματος 5.2 είναι πλήρης
και άρα το Θεώρημα 5.7 έχει επίσης αποδειχτεί πλήρως.
. Η απόδειξη του Λήμματος 5.2 είναι πλήρης
και άρα το Θεώρημα 5.7 έχει επίσης αποδειχτεί πλήρως.
Mihalis Kolountzakis 2015-11-28