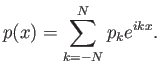Next: 2.6 Προβλήματα Up: 2. Τριγωνομετρικά πολυώνυμα Previous: 2.4 Εσωτερικό γινόμενο και Contents Index
Μια συνάρτηση
![]() λέγεται άρτια αν
λέγεται άρτια αν
![]() για κάθε
για κάθε
![]() (οποιοδήποτε πεδίο ορισμού
(οποιοδήποτε πεδίο ορισμού ![]() μπορούμε να έχουμε εδώ το οποίο είναι συμμετρικό ως προς το 0, ισχύει δηλ.
μπορούμε να έχουμε εδώ το οποίο είναι συμμετρικό ως προς το 0, ισχύει δηλ.
![]() ).
Η
).
Η
![]() λέγεται περιττή αν ισχύει
λέγεται περιττή αν ισχύει
![]() για κάθε
για κάθε
![]() .
.
Είναι φανερό ότι το να είναι μια συνάρτηση άρτια ή περιττή είναι μια σχετικά σπάνια ιδιότητα; οι «πιο πολλές» συναρτήσεις δεν είναι ούτε το ένα ούτε το άλλο. Παρ' όλ' αυτά ισχύει το παρακάτω θεώρημα το οποίο κάποιες φορές μας επιτρέπει να περάσουμε ιδιότητες των αρτίων και των περιττών συναρτήσεων σε γενικές συναρτήσεις.
Η απόδειξη είναι εξαιρετικά απλή. Παίρνουμε
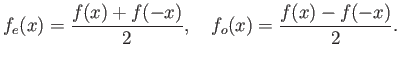
Για να δείξουμε τη μοναδικότητα υποθέτουμε ότι υπάρχει και δεύτερη διάσπαση της ![]() σε άθροισμα άρτιας και περιττής
συνάρτησης
σε άθροισμα άρτιας και περιττής
συνάρτησης
Οι συναρτήσεις ![]() και
και ![]() ονομάζονται άρτιο και περιττό μέρος της
ονομάζονται άρτιο και περιττό μέρος της ![]() .
.