Next: 2.4 Εσωτερικό γινόμενο και Up: 2. Τριγωνομετρικά πολυώνυμα Previous: 2.2 Περιοδικότητα Contents Index
Ένα τριγωνομετρικό πολυώνυμο είναι ένας πεπερασμένος γραμμικός συνδυασμός,
με μιγαδικούς συντελεστές, μιγαδικών εκθετικών συναρτήσεων με περίοδο ![]() , δηλ. των συναρτήσεων
, δηλ. των συναρτήσεων
Τα ![]() στην (2.3) ονομάζονται συντελεστές του
στην (2.3) ονομάζονται συντελεστές του ![]() και καθορίζονται μοναδικά.
Δε μπορεί δηλ. η ίδια συνάρτηση
και καθορίζονται μοναδικά.
Δε μπορεί δηλ. η ίδια συνάρτηση ![]() να γραφεί με δυο διαφορετικούς τρόπους στη γραφή (2.3).
να γραφεί με δυο διαφορετικούς τρόπους στη γραφή (2.3).
Είναι σημαντικό να τονίσουμε ότι τα τριγωνομετρικά πολυώνυμα είναι ![]() -περιοδικές, συνεχείς
συναρτήσεις αφού κάθε συνάρτηση
-περιοδικές, συνεχείς
συναρτήσεις αφού κάθε συνάρτηση
![]() είναι τέτοια.
είναι τέτοια.
Υπόδειξη: Αρκεί να δείξουμε ότι αν
![]() για κάθε
για κάθε
![]() τότε
τότε ![]() για
κάθε
για
κάθε ![]() . Δείξτε ότι αρκεί ο
. Δείξτε ότι αρκεί ο
![]() πίνακας με στοιχεία τα
πίνακας με στοιχεία τα
![]() ,
,
![]() ,
,
![]() , να είναι αντιστρέψιμος.
, να είναι αντιστρέψιμος.
Αυτό ανάγεται σε ένα πίνακα Vandermonde ![]() με
με
![]() ,
,
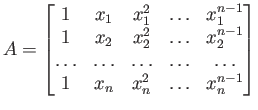

Υπόδειξη: Ένας άλλος τρόπος να αποδείξετε ότι ένα τριγωνομετρικό πολυώνυμο βαθμού ![]() το οποίο
μηδενίζεται σε
το οποίο
μηδενίζεται σε ![]() σημεία έχει όλους τους συντελεστές του μηδενικούς
είναι να χρησιμοποιήσετε την αντίστοιχη πρόταση για τα αλγεβρικά πολυώνυμα,
ότι δηλ. ένα αλγεβρικό πολυώνυμο βαθμού
σημεία έχει όλους τους συντελεστές του μηδενικούς
είναι να χρησιμοποιήσετε την αντίστοιχη πρόταση για τα αλγεβρικά πολυώνυμα,
ότι δηλ. ένα αλγεβρικό πολυώνυμο βαθμού ![]() που μηδενίζεται σε
που μηδενίζεται σε ![]() σημεία στο
σημεία στο
![]() είναι αναγκαστικά
το μηδενικό πολυώνυμο, αυτό δηλ. με όλους τους συντελεστές ίσους με το μηδέν. Χρησιμοποιήστε το
πολυώνυμο
είναι αναγκαστικά
το μηδενικό πολυώνυμο, αυτό δηλ. με όλους τους συντελεστές ίσους με το μηδέν. Χρησιμοποιήστε το
πολυώνυμο
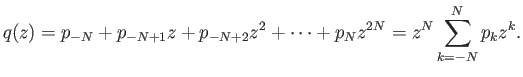
Mihalis Kolountzakis 2015-11-28