5.3 Υπογραφήματα και ισομορφία

5.3.1 Υπογραφήματα

Ορισμός 5.4   (Υπογράφημα) Ενα γράφημα $G'=(V', E')$ θα λέγεται υπογράφημα ενός γραφήματος $G=(V,E)$ αν $V' \subseteq V$ και $E' \subseteq E$.

Με άλλα λόγια, το $G'$ είναι υπογράφημα του $G$ αν μπορούμε να το πάρουμε από το $G$ αφαιρώντας κάποιες κορυφές και κάποιες ακμές. Εννοείται εδώ ότι αν αποφασίσουμε να αφαιρέσουμε από το $G$ μια κορυφή $u$ αυτόματα διαγράφουμε και όλες τις ακμές που περιέχουν την $u$, μια και δεν έχουν πλέον «νόημα».

Σχήμα 5.10: Το δεξί γράφημα είναι υπογράφημα του αριστερού

Παράδειγμα 5.5   Στο Σχήμα 5.10 το γράφημα δεξιά είναι υπογράφημα του γραφήματος αριστερά. Παρατηρήστε ότι το γράφημα δεξιά είναι ζωγραφισμένο «διαφορετικά» απ' ότι το αντίστοιχό του αριστερά. Ας τονίσουμε εδώ ότι αυτό δεν έχει σημασία, μια και ένα γράφημα μπορεί να ζωγραφιστεί με πολλούς τρόπους στο επίπεδο. Αυτό που έχει σημασία είναι το ποια συνδεσμολογία (ποιες ακμές) υποδηλώνονται από το σχήμα. Από κει και πέρα είμαστε ελεύθεροι να επιλέξουμε να παραστήσουμε το γράφημα ως σχήμα με όποιο τρόπο προσφέρεται για τους σκοπούς μας.

Άσκηση 5.9   Πόσες ακμές έχει το πλήρες γράφημα $K_n$; Πόσα υπογραφήματα έχει το $K_n$;

Υπόδειξη: Για το πρώτο ερώτημα, αφού υπάρχουν όλες οι δυνατές ακμές τότε για να καθορίσουμε μια ακμή αρκεί να προσδιορίσουμε το ζεύγος των κορυφών της. Για το δεύτερο ερώτημα, για να καθοριστεί ένα υπογράφημα πρέπει (α) να καθορίσουμε ποιο θα είναι το σύνολο των κορυφών του (ένα οποιοδήποτε υποσύνολο του $[n]$) και (β) αφού προσδιορίσουμε το ποιες είναι οι κορυφές του υπογραφήματος θα πρέπει να αποφασίσουμε το ποιες είναι οι ακμές του. Το πλήθος των επιλογών στο (β) εξαρτάται προφανώς από το πόσες κορυφές επιλέξαμε στο (α). Π.χ. αν στο βήμα (α) επιλέξαμε 5 κορυφές στο βήμα (β) έχουμε να διαλέξουμε ένα οποιοδήποτε υποσύνολο όλων των δυνατών ακμών, των οποίων το πλήθος είναι ${5 \choose 2}$.

Έτσι, η απάντηση στο τελευταίο είναι ένα άθροισμα (για όλα τα $k=0,1,\ldots,n$, όπου $k$ συμβολίζει το πόσες κορυφές επιλέξαμε στο βήμα (α)) που μάλλον δεν απλοποιείται.

Μια ειδική κατηγορία υπογραφημάτων είναι τα λεγόμενα επαγόμενα υπογραφήματα, τα οποία προκύπτουν από ένα γράφημα διαγράφοντας απλώς ορισμένες κορυφές και χωρίς περιττές διαγραφές ακμών.

Ορισμός 5.5   Αν $V' \subseteq V$, τότε το υπογράφημα του $G=(V,E)$ που επάγεται από το σύνολο κορυφών $V'$ είναι το γράφημα $G'=(V', E')$, με

$$E' = {\left\{{e={\left\{{u,v}\right\}}\in E: u,v \in V'}\right\}}.$$

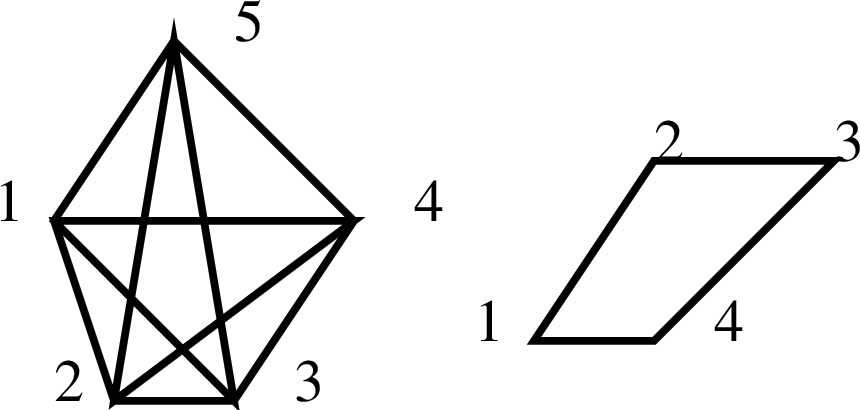
Δείτε το Σχήμα 5.11 για παράδειγμα.

Στο Σχήμα 5.10 το γράφημα δεξιά δεν είναι επαγόμενο υπογράφημα αφού λείπουν οι ακμές ${\left\{{2,4}\right\}}$ και ${\left\{{1,3}\right\}}$. Αν τις προσθέσουμε σε αυτό τότε γίνεται το υπογράφημα του αριστερού γραφήματος που επάγεται από το σύνολο κορυφών $V={\left\{{1,2,3,4}\right\}}$.

Σχήμα 5.11: Το γράφημα δεξιά είναι αυτό που επάγουν οι κόκκινες κορυφές στο γράφημα αριστερά

Άσκηση 5.10   Πόσα επαγόμενα υπογραφήματα έχει ένα γράφημα με $n$ κορυφές;

Υπόδειξη: Για ένα δεδομένο γράφημα $G$ ένα επαγόμενο υπογράφημά του είναι πλήρως καθορισμένο αν καθορίσουμε το ποιες είναι οι κορυφές του $G$ που το επάγουν (σύνολο $V'$ στον Ορισμό 5.5).

5.3.2 Ισομορφία γραφημάτων

Ορισμός 5.6   Δύο γραφήματα $G=(V,E)$ και $G'=(V', E')$, με ίδιο πλήθος κορυφών, λέγονται ισόμορφα ή ισομορφικά αν υπάρχει μια 1-1 και επί συνάρτηση $f:V\to V'$ τέτοια ώστε να έχουμε

$$\forall u,v \in V: \left( u \stackrel{G}{\sim} v \Longleftrightarrow f(u) \stackrel{G'}{\sim} f(v) \right).$$ (5.1)

Με άλλα λόγια, δυο γραφήματα λέγονται ισόμορφα αν μπορούμε να αντιστοιχίσουμε τις κορυφές τους 1-1 με τέτοιο τρόπο ώστε να διατηρείται η συνδεσμολογία.

Δείτε το Σχήμα 5.12 για παράδειγμα.

Σχήμα 5.12: Τα δύο γραφήματα είναι ισόμορφα με την αντιστοίχιση κορυφών (συνάρτηση $f$ στον Ορισμό 5.6) $\alpha \to 1, \beta \to 2, \gamma \to 3, \delta \to 4, \epsilon \to 5$

Άσκηση 5.11   Δείξτε ότι η ισομορφία γραφημάτων είναι μια σχέση ισοδυναμίας. Δηλ. αν $F$.$G$ και $H$ είναι απλά γραφήματα τότε:

• Ανακλαστική ιδιότητα: $F$ είναι ισόμορφο με το $F$,
• Συμμετρική ιδιότητα: Αν το $F$ είναι ισόμορφο με το $G$ τότε και το $G$ είναι ισόμορφο με το $F$, και
• Μεταβατική ιδιότητα: Αν $F$ ισόμορφο με το $G$ και $G$ ισόμορφο με το $H$ τότε και το $F$ είναι ισόμορφο με το $H$.

Σχήμα 5.13: Δείξτε ότι τα δύο γραφήματα δεν είναι ισόμορφα

Σχήμα 5.14: Τα μη-ισόμορφα γραφήματα με 3 κορυφές

Παράδειγμα 5.6   Στο Σχήμα 5.14 δείχνουμε όλα τα μη-ισόμορφα μεταξύ τους γραφήματα με 3 κορυφές. Κάθε άλλο δηλ. γράφημα με 3 κορυφές (φαίνονται στο Σχήμα 5.4) είναι ισόμορφο ακριβώς με ένα από τα 4 αυτά γραφήματα. Παρατηρήστε ότι το πλήθος τους είναι κατά πολύ μικρότερο του πλήθος όλων των γραφημάτων με 3 κορυφές, ισομόρφων μεταξύ τους ή όχι.

Η απεικόνιση $f$ (που ονομάζεται ισομορφισμός) δεν είναι μοναδικά καθορισμένη και ούτε είναι συνήθως προφανής η ύπαρξή της. Π.χ. η απεικόνιση $f$ από το γράφημα του Σχήματος 5.16 στο γράφημα του Σχήματος 6.1 που έχει

$$f(1)=1, f(2)=5, f(3)=6, f(4)=7, f(5)=4, f(6)=3, f(7)=2,$$

είναι κι αυτή ένας ισομορφισμός από το πρώτο γράφημα στο δεύτερο.

Οσον αφορά τη θεωρία γραφημάτων, δύο ισόμορφα γραφήματα συνήθως δεν τα ξεχωρίζουμε μεταξύ τους. Π.χ. θα θεωρούμε ένα γράφημα $G$ υπογράφημα ενός γραφήματος $G'$ αν το $G$ είναι ισόμορφο με κάποιο υπογράφημα του $G'$. Ετσι το γράφημα

$$\alpha - \beta - \gamma$$

(τρείς κορυφές και δύο ακμές) θεωρείται υπογράφημα του γραφήματος του Σχήματος 6.1 παρά το ότι το σύνολο κορυφών του δεν είναι καν υποσύνολο του συνόλου των κορυφών του Σχήματος 6.1.

Άσκηση 5.12   Δείξτε ότι κάθε απλό γράφημα $G$ είναι ισομορφικό με κάποιο υπογράφημα του πλήρους γραφήματος $K_n$, όπου $n$ είναι το πλήθος των κορυφών του $G$.

Άσκηση 5.13   Δείξτε ότι δύο ισομορφικά γραφήματα έχουν το ίδιο πλήθος ακμών.

Άσκηση 5.14   Δείξτε ότι τα δύο γραφήματα του Σχήματος 5.13 δεν είναι ισόμορφα.

Άσκηση 5.15   Δείξτε ότι δύο γραφήματα είναι ισομορφικά αν και μόνο αν τα συμπληρώματά τους (δείτε Άσκ. 5.1) είναι ισομορφικά.

Άσκηση 5.16   Βρείτε ένα γράφημα με 5 κορυφές που να είναι ισομορφικό με το συμπληρωματικό του (δείτε Άσκ. 5.1).

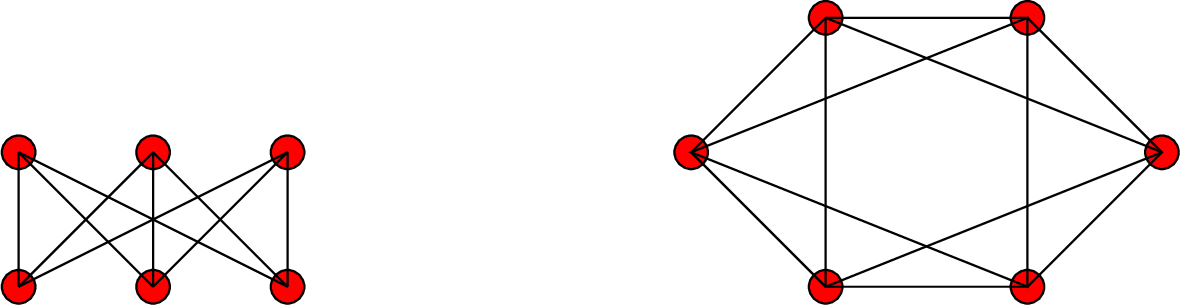
Υπόδειξη: 5 κορυφές ορίζουν ${5 \choose 2} = 10$ ακμές, άρα το γράφημα αυτό και το συμπληρωματικό του, αφού είναι ισόμορφα, θα έχουνε τον ίδιο αριθμό ακμών, δηλ. 5 ακμές το καθένα.

Άσκηση 5.17   Θεωρήστε το γράφημα $W$ που έχει ως κορυφές τις ημέρες της εβδομάδας, και όπου δύο μέρες συνδέονται μεταξύ τους με ακμή αν και μόνο αν η μια είναι η επόμενη της άλλης. Επίσης το γράφημα $S$ με σύνολο κορυφών το ${\left\{{0,1,\ldots,6}\right\}}$ όπου δύο κορυφές συνδέονται μεταξύ τους αν και μόνο αν η διαφορά τους $\bmod 7$ ισούται με 3 ή 4 (με άλλα λόγια είναι 3 ή -3 ${} \bmod 7$). Σχεδιάστε τα δύο γραφήματα και δείξτε ότι είναι ισόμορφα.

Άσκηση 5.18   Θεωρήστε το γράφημα $Q$ που έχει ως κορυφές του τις κορυφές ενός τρισδιάστατου κύβου, και το γράφημα $B$ που έχει ως κορυφές όλα τα στοιχεία του συνόλου ${\left\{{0,1}\right\}}^3$, όλες δηλ. τις τριάδες από 0 ή 1. Δύο κορυφές του $Q$ συνδέονται αν και μόνο αν συνδέονται με μια ακμή του κύβου. Δύο τριάδες συνδέονται στο $B$ αν και μόνο αν διαφέρουν σε μια ακριβώς συντεταγμένη. Δείξτε ότι τα $Q$ και $B$ είναι ισόμορφα.

Δείτε το Σχήμα 5.15.

Σχήμα 5.15: Το γράφημα της Άσκησης 5.18 που φτιάχνεται από τις κορυφές του κύβου

Το να αποφασίσει κανείς ότι δύο γραφήματα είναι ισόμορφα απαιτεί συνήθως αρκετή δουλειά, μια και, κατ' αρχήν τουλάχιστον, πρέπει να εξετάσει κάθε μια από τις δυνατές συναρτήσεις που απεικονίζουν τις κορυφές του ενός γραφήματος στις κορυφές ενός άλλου και να ελέγξει αν είναι ισομορφισμός. Όμως πολλές φορές μπορεί κανείς να αποφανθεί ότι δύο γραφήματα δεν είναι ισόμορφα χρησιμοποιώντας κάποια απλά κριτήρια, όπως αυτά της Άσκησης 5.19.

Άσκηση 5.19   Έστω $G$ και $H$ δύο απλά γραφήματα. Δείξτε ότι σε κάθε μια από τις παρακάτω περιπτώσεις αυτά δεν είναι ισόμορφα.

1. ${\left\vert{V(G)}\right\vert} \neq {\left\vert{V(H)}\right\vert}$
2. ${\left\vert{E(G)}\right\vert} \neq {\left\vert{E(H)}\right\vert}$
3. Ο μέγιστος βαθμός κορυφής του $G$ είναι διαφορετικός από το μέγιστο βαθμό κορυφής του $H$.
4. κάθε κορυφή του $G$ συνδέεται με κάθε άλλη με κάποιο μονοπάτι, ενώ υπάρχουν δύο κορυφές του $H$ που δε συνδέονται μεταξύ τους με μονοπάτι.

Δείξτε επίσης ότι υπάρχουν δύο μη ισόμορφα γραφήματα $G$ και $H$ στα οποία δεν ισχύει κανένα από τα παραπάνω κριτήρια μη ισομορφίας.

Παρατήρηση 5.1   Ένας άλλος τρόπος να περιγράψει κανείς το πότε δύο γραφήματα είναι μεταξύ τους ισόμορφα είναι να κάνει την παρατήρηση ότι είναι ισόμορφα αν και μόνο αν, μπορεί κανείς να πάρει από το ένα το άλλο, απλά με μια μετονομασία των κορυφών τους.

Άσκηση 5.20   Βρείτε όλα τα μη-ισόμορφα γραφήματα με τέσσερεις κορυφές.

Άσκηση 5.21   Βεβαιωθείτε ότι τα δύο γραφήματα του Σχ. 6.1 είναι ισόμορφα μεταξύ τους.