Ένα γράφημα (μερικές φορές στην ελληνική βιβλιογραφία γίνεται λόγος και
για ένα γράφο) είναι ο βασικότερος, παραστατικότερος και πλέον εύχρηστος
γενικός τρόπος στα Μαθηματικά (αλλά και στις Επιστήμες γενικότερα) να
παραστήσει κανείς πληροφορία συνδεσμολογίας, να περιγράψει δηλ. μια ομάδα αντικειμένων
μερικά από τα οποία συνδέονται μεταξύ τους, και ενδεχομένως και πληροφορίες
για τη συνδεσμολογία.
Ορισμός 5.1
(Απλό γράφημα)
Ενα απλό γράφημα 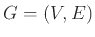 αποτελείται από ένα σύνολο
κορυφών
αποτελείται από ένα σύνολο
κορυφών 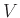 και ένα σύνολο ακμών
και ένα σύνολο ακμών 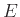 ,
το οποίο είναι ένα σύνολο από δισύνολα του
,
το οποίο είναι ένα σύνολο από δισύνολα του 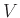 .
Γράφουμε επίσης
.
Γράφουμε επίσης 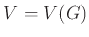 και
και 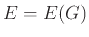 για τα σύνολα κορυφών
και ακμών του γραφήματος
για τα σύνολα κορυφών
και ακμών του γραφήματος 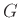 .
.
Μια ακμή ανάμεσα σε δύο κορυφές 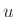 και
και 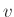 αντιπροσωπεύει κάποια έννοια
σύνδεσης των δύο κορυφών.
Συνηθίζουμε να παριστάνουμε ένα γράφημα αντιστοιχώντας ένα σημείο
του επιπέδου σε κάθε κορυφή και τραβώντας μια γραμμή που ενώνει
δυο κορυφές αν και μόνο αν αυτές ενώνονται με μια ακμή στο
αντιπροσωπεύει κάποια έννοια
σύνδεσης των δύο κορυφών.
Συνηθίζουμε να παριστάνουμε ένα γράφημα αντιστοιχώντας ένα σημείο
του επιπέδου σε κάθε κορυφή και τραβώντας μια γραμμή που ενώνει
δυο κορυφές αν και μόνο αν αυτές ενώνονται με μια ακμή στο 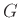 .
.
Επισημαίνουμε εδώ ότι αυτή η γραφική παράσταση ενός γραφήματος
έχει εποπτική μόνο σημασία. Υπάρχουν γραφήματα στα οποία δε χρησιμοποιούμε ποτέ
κάποια γραφική παράσταση (συνήθως λόγω μεγέθους) και τα γραφήματα που μπορούν
να παρασταθούν γραφικά με διάφορους τρόπους.
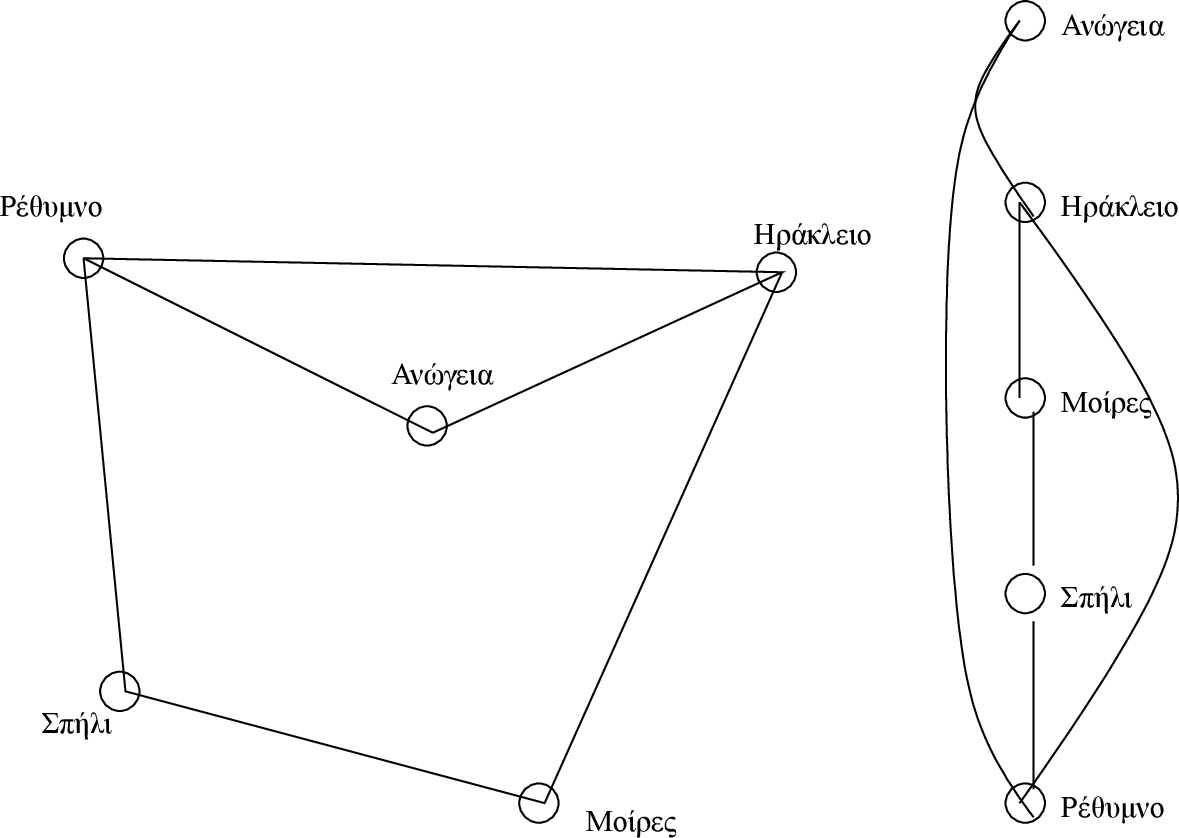
Σχήμα
5.1: Κάποιες πόλεις στην Κρήτη και οδικές συνδέσεις
ως γράφημα
Για παράδειγμα, στο Σχήμα 5.1 δείχνουμε με δύο διαφορετικούς
τρόπους το ίδιο γράφημα που σκοπό έχει να δείξει την οδική συνδεσμολογία
ανάμεσα σε πέντε πόλεις της Κρήτης. Η ύπαρξη μιας ακμής ανάμεσα
σε δύο κορυφές (πόλεις) υποδηλώνει την ύπαρξη ενός δρόμου.
Το σύνολο κορυφών σε αυτό το γράφημα είναι το
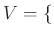
Ηράκλειο, Ρέθυμνο, Ανώγεια, Μοίρες, Σπήλι
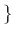
ενώ το σύνολο ακμών είναι το
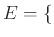
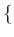
Ηράκλειο, Ρέθυμνο
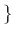
,
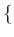
Ηράκλειο, Ανώγεια
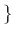
,
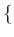
Ανώγεια, Ρέθυμνο
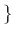
,
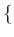
Ρέθυμνο, Σπήλι
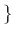
,
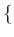
Σπήλι, Μοίρες
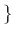
,
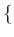
Μοίρες, Ηράκλειο
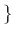
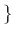
.
Στην αριστερή γραφική παράσταση του γραφήματος έχουμε ζωγραφίσει
τις πόλεις σε τέτοια θέση ώστε η σχετική τους θέση να μοιάζει με αυτή που έχουν
πάνω στο χάρτη, ενώ δεξιά έχουμε ζωγραφίσει το ίδιο γράφημα βάζοντας απλά
όλες τις πόλεις τη μια κάτω από την άλλη σε αλφαβητική σειρά.
Τονίζουμε ξανά ότι και τα δύο σχέδια παριστάνουν το ίδιο γράφημα.
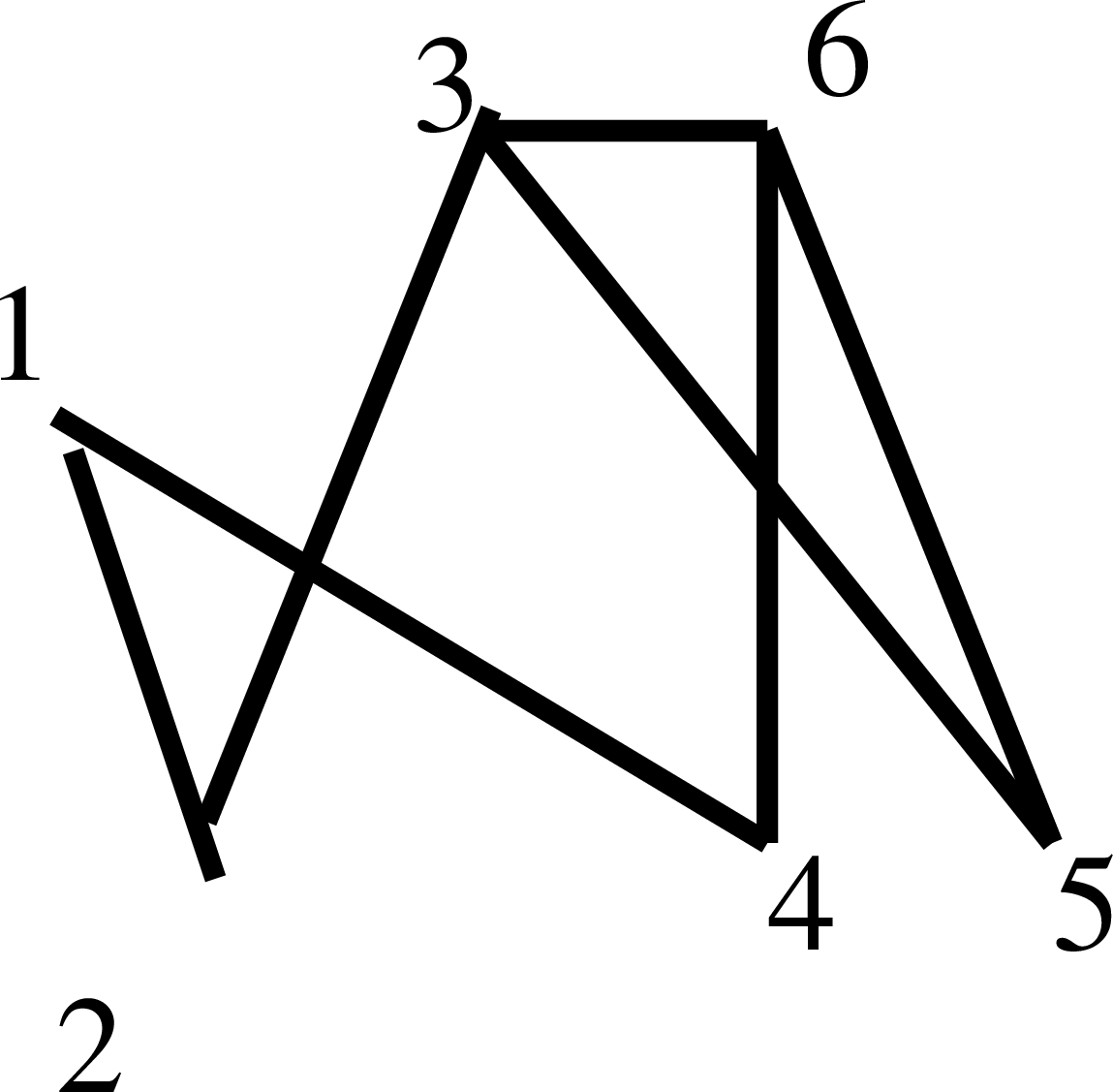
Σχήμα
5.2: Ενα απλό γράφημα με 6 κορυφές και 7 ακμές
Παράδειγμα 5.1
Συνήθως τα ονόματα που επιλέγουμε για τις κορυφές είναι απλά αριθμοί. Ένα τυπικό
γράφημα είναι π.χ.
το γράφημα του Σχήματος 5.2 που έχει
σύνολο κορυφών το
και σύνολο ακμών το
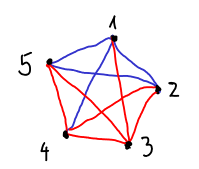
Σχήμα
5.3: Εδώ βλέπουμε δύο συμπληρωματικά γραφήματα με κοινό σύνολο κορυφών
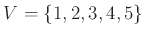
. Τα δύο γραφήματα είναι αυτό με τις μπλε και αυτό με τις κόκκινες ακμές.
Κάθε δυνατή ακμή ανάμεσα σε στοιχεία του
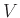
είναι χρωματισμένη είτε μπλε είτε κόκκινη.
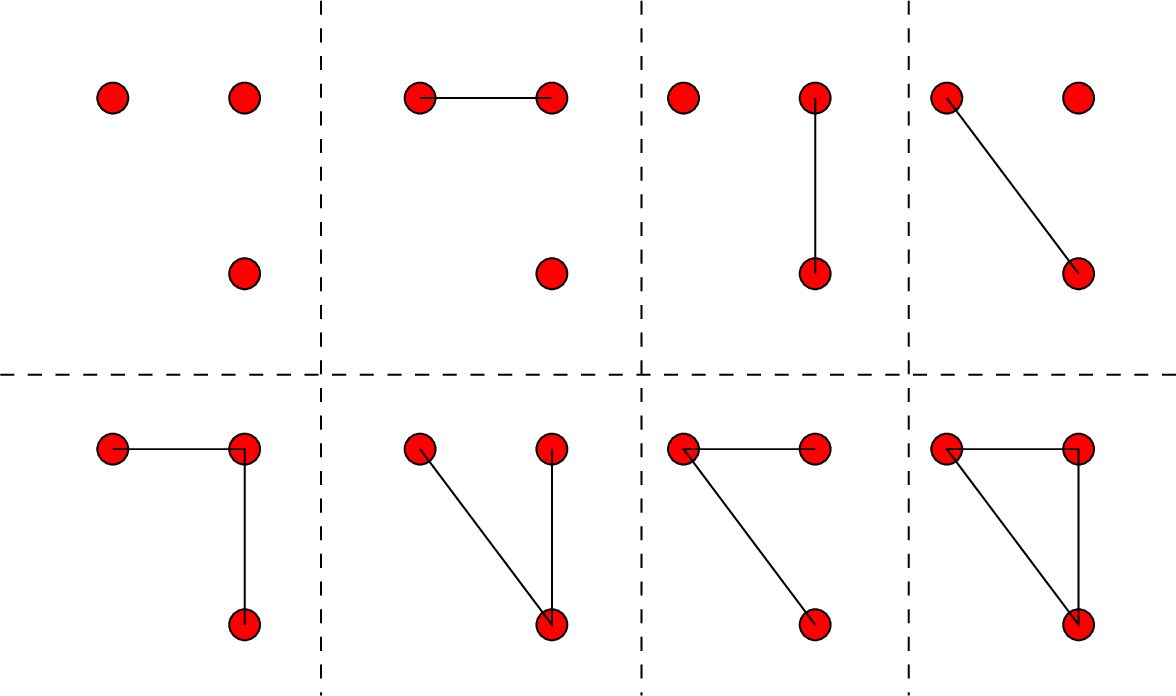
Σχήμα
5.4: Τα διαφορετικά απλά γραφήματα με 3 κορυφές
Παράδειγμα 5.2
Στο Σχήμα 5.4
δείχνουμε όλα τα διαφορετικά απλά γραφήματα με 3 κορυφές.
Άσκηση 5.2
Πόσα διαφορετικά γραφήματα υπάρχουν με 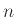 κορυφές;
Πόσα με
κορυφές;
Πόσα με 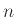 κορυφές και
κορυφές και  ακμές; (
ακμές; (
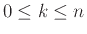 )
)
Αν δυο κορυφές 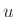 και
και 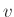 ενώνονται στο
ενώνονται στο 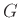 (δηλ. αν
(δηλ. αν
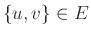 ) θα γράφουμε συνήθως
) θα γράφουμε συνήθως
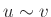 ή και
ή και
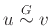 αν θέλουμε να
τονίσουμε για ποιο γράφημα μιλάμε.
Ομοίως θα γράφουμε
αν θέλουμε να
τονίσουμε για ποιο γράφημα μιλάμε.
Ομοίως θα γράφουμε
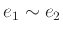 για δύο ακμές
για δύο ακμές 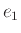 και
και 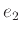 αν αυτές μοιράζονται μια από τις δυό τους κορυφές.
αν αυτές μοιράζονται μια από τις δυό τους κορυφές.
Ορισμός 5.2
(Γειτονικές κορυφές και ακμές, γειτονιές)
Δύο κορυφές που συνδέονται με ακμή
(αντ. ακμές που έχουν μια κοινή κορυφή) θα λέγονται γειτονικές
ή γείτονες και το σύνολο των γειτόνων μιας κορυφής (αντ. ακμής)
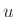 θα λέγεται η γειτονιά του
θα λέγεται η γειτονιά του 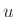 και θα συμβολίζεται
συνήθως με
και θα συμβολίζεται
συνήθως με 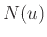 .
.
Δείτε το Σχήμα 5.5 για παράδειγμα.
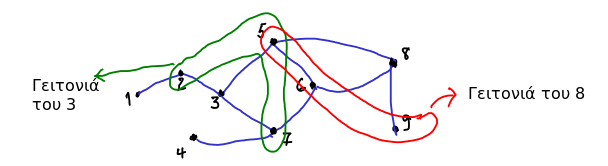
Σχήμα
5.5: Στο γράφημα αυτό φαίνεται με πράσινο χρώμα η γειτονιά της κορυφής 3 (οι κορυφές 2, 5, 7)
και με κόκκινο χρώμα η γειτονιά της κορυφής 8 (οι κορυφές 5, 6, 9)
Παράδειγμα 5.3
Στο γράφημα του Σχήματος 5.2 έχουμε
Η γειτονιά της ακμής
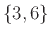 είναι το σύνολο ακμών
είναι το σύνολο ακμών
Παρατηρήστε ότι μια ακμή είναι πάντα γείτονας του εαυτού της σύμφωνα
με τον ορισμό που έχουμε δώσει, ενώ μια κορυφή ποτέ δε γειτονεύει
με τον εαυτό της σε ένα απλό γράφημα (αυτό αλλάζει αργότερα όταν θα εξετάζουμε
γενικότερα γραφήματα).
Δείτε το Σχήμα 5.6 για παράδειγμα ενός κανονικού γραφήματος.
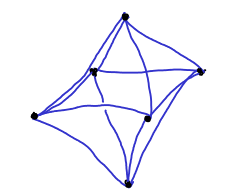
Σχήμα
5.6: Ένα κανονικό γράφημα βαθμού 4 με 6 κορυφές
Παράδειγμα 5.4
Στο Σχήμα 5.2, αν σβήσουμε την ακμή
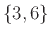 ,
όλες οι κορυφές έχουν βαθμό 2, άρα είναι
το γράφημα αυτό 2-κανονικό.
Στο Σχήμα 5.1 ο βαθμός των κορυφών Ηράκλειο και Ρέθυμνο
είναι 3 και των άλλων κορυφών είναι 2.
,
όλες οι κορυφές έχουν βαθμό 2, άρα είναι
το γράφημα αυτό 2-κανονικό.
Στο Σχήμα 5.1 ο βαθμός των κορυφών Ηράκλειο και Ρέθυμνο
είναι 3 και των άλλων κορυφών είναι 2.
Άσκηση 5.3
Γίνεται σε ένα γράφημα όλες οι κορυφές να έχουν διαφορετικό βαθμό;
Υπόδειξη: Οι δυνατές τιμές για το βαθμό μιας κορυφής σε ένα γράφημα με 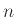 κορυφές είναι
κορυφές είναι
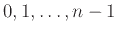 .
Μπορούμε να έχουμε κορυφή βαθμού 0 και κορυφή βαθμού
.
Μπορούμε να έχουμε κορυφή βαθμού 0 και κορυφή βαθμού 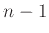 ταυτόχρονα;
ταυτόχρονα;
Άσκηση 5.4
Δείξτε ότι σε ένα γράφημα 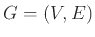 το άθροισμα των βαθμών όλων
των κορυφών ισούται με
το άθροισμα των βαθμών όλων
των κορυφών ισούται με
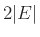 .
.
Άσκηση 5.6
Δείξτε ότι σε οποιοδήποτε γράφημα το πλήθος κορυφών με
περιττό βαθμό είναι άρτιο.
Άσκηση 5.7
Αν 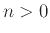 δείξτε ότι υπάρχει
δείξτε ότι υπάρχει 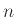 -κανονικό γράφημα με
-κανονικό γράφημα με 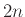 κορυφές.
κορυφές.
Άσκηση 5.8
Ένα σύνολο κορυφών ενός γραφήματος λέγεται ανεξάρτητο αν κάθε δύο κορυφές του
δε συνδέεονται με ακμή.
Επίσης, ένα σύνολο κορυφών λέγεται κάλυμμα αν κάθε ακμή του γραφήματος περιέχει
κάποια από τις κορυφές αυτές.
Δείξτε ότι σ' ένα γράφημα 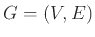 το σύνολο κορυφών
το σύνολο κορυφών
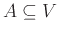 είναι ανεξάρτητο
αν και μόνο αν το σύνολο κορυφών
είναι ανεξάρτητο
αν και μόνο αν το σύνολο κορυφών
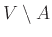 είναι κάλυμμα.
είναι κάλυμμα.
Δείτε το Σχήμα 5.7 για παράδειγμα.
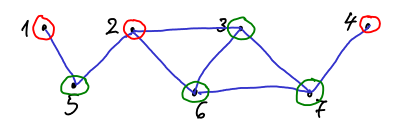
Σχήμα
5.7: Στο γράφημα αυτό οι κόκκινες κορυφές αποτελούν ανεξάρτητο σύνολο
και το συμπλήρωμά τους, οι πράσινες κορυφές, αποτελούν κάλυμμα
Mihalis Kolountzakis
2015-11-28




![]() και
και ![]() ενώνονται στο
ενώνονται στο ![]() (δηλ. αν
(δηλ. αν
![]() ) θα γράφουμε συνήθως
) θα γράφουμε συνήθως
![]() ή και
ή και
![]() αν θέλουμε να
τονίσουμε για ποιο γράφημα μιλάμε.
Ομοίως θα γράφουμε
αν θέλουμε να
τονίσουμε για ποιο γράφημα μιλάμε.
Ομοίως θα γράφουμε
![]() για δύο ακμές
για δύο ακμές ![]() και
και ![]() αν αυτές μοιράζονται μια από τις δυό τους κορυφές.
αν αυτές μοιράζονται μια από τις δυό τους κορυφές.

![]() τότε λέγεται
τότε λέγεται
![]() -κανονικό.
-κανονικό.
![]() κορυφές είναι
κορυφές είναι
![]() .
Μπορούμε να έχουμε κορυφή βαθμού 0 και κορυφή βαθμού
.
Μπορούμε να έχουμε κορυφή βαθμού 0 και κορυφή βαθμού ![]() ταυτόχρονα;
ταυτόχρονα;![]() το σύνολο κορυφών
το σύνολο κορυφών
![]() είναι ανεξάρτητο
αν και μόνο αν το σύνολο κορυφών
είναι ανεξάρτητο
αν και μόνο αν το σύνολο κορυφών
![]() είναι κάλυμμα.
είναι κάλυμμα.
