Next: 5.5 Δέντρα και δάση Up: 5. Εισαγωγή στη θεωρία Previous: 5.3 Υπογραφήματα και ισομορφία Contents Index
Ένα μονοπάτι μπορεί να χρησιμοποιεί μια ακμή του γραφήματος παραπάνω από μια φορά.
Οταν θέλουμε να μιλήσουμε για κυκλώματα χωρίς επαναλαμβανόμενες ακμές θα τα αποκαλούμε κύκλους.
Είναι εύκολο να δειχτεί ότι η σχέση «![]() προσιτό από
προσιτό από ![]() » είναι μία
σχέση ισοδυναμίας πάνω στο σύνολο
» είναι μία
σχέση ισοδυναμίας πάνω στο σύνολο ![]() των κορυφών.
Άρα το σύνολο
των κορυφών.
Άρα το σύνολο ![]() διαμερίζεται σε κλάσεις ισοδυναμίας που
τις ονομάζουμε συνεκτικές συνιστώσες.
Με άλλα λόγια δύο κορυφές ενός γραφήματος είναι στην ίδια συνεκτική συνιστώσα
αν και μόνο αν υπάρχει μονοπάτι που τις ενώνει.
διαμερίζεται σε κλάσεις ισοδυναμίας που
τις ονομάζουμε συνεκτικές συνιστώσες.
Με άλλα λόγια δύο κορυφές ενός γραφήματος είναι στην ίδια συνεκτική συνιστώσα
αν και μόνο αν υπάρχει μονοπάτι που τις ενώνει.
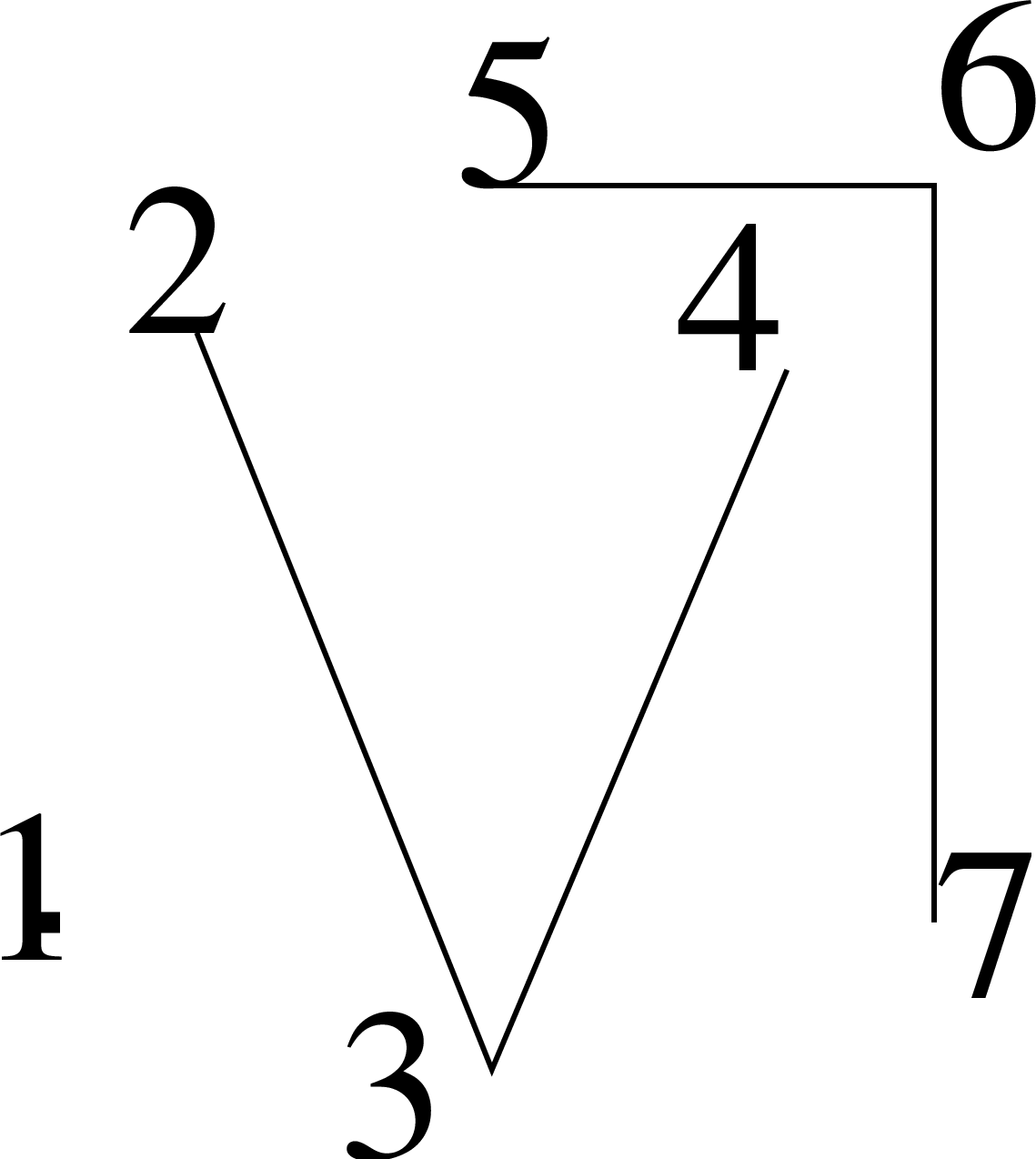
Υπόδειξη: Υποθέστε ότι δεν ισχύει το συμπέρασμα και καταλήξετε σε άτοπο χρησιμοποιώντας την Άσκηση 5.4.
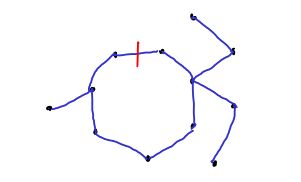
Θα ορίσουμε τώρα μια συνάρτηση
![]() που θα έχει την έννοια
της απόστασης. Η ποσότητα δηλ.
που θα έχει την έννοια
της απόστασης. Η ποσότητα δηλ. ![]() θα «μετράει» το πόσο κοντά είναι
οι δύο κορυφές
θα «μετράει» το πόσο κοντά είναι
οι δύο κορυφές ![]() και
και ![]() του γραφήματος.
του γραφήματος.
Αλλιώς ορίζουμε ![]() να είναι το ελάχιστο μήκος μονοπατιού
που συνδέει τις
να είναι το ελάχιστο μήκος μονοπατιού
που συνδέει τις ![]() και
και ![]() , δηλ. του μονοπατιού εκείνου με τις
λιγότερες ακμές.
, δηλ. του μονοπατιού εκείνου με τις
λιγότερες ακμές.
Οπως κάθε φυσιολογική έννοια απόστασης στα Μαθηματικά, η συνάρτηση απόστασης που μόλις ορίσαμε ικανοποιεί τη λεγόμενη τριγωνική ανισότητα:
Εχοντας ορίσει μια έννοια απόστασης, μπορούμε τώρα να μιλήσουμε για τη
διάμετρο ενός γραφήματος ![]() , που τη συμβολίζουμε
με
, που τη συμβολίζουμε
με
![]() .
.
Περιγράψτε, με πλήρη απόδειξη,
όλα τα γραφήματα με ![]() κορυφές και διάμετρο
κορυφές και διάμετρο ![]() .
.
Επίσης όλα τα γραφήματα με διάμετρο ![]() και όλα τα γραφήματα με
διάμετρο 1.
και όλα τα γραφήματα με
διάμετρο 1.
Υπόδειξη: Για το πρώτο παρατηρήστε ότι
αν ![]() είναι δυο κορυφές του
είναι δυο κορυφές του ![]() με απόσταση
με απόσταση
![]() τότε
υπάρχει ένα μονοπάτι που τις ενώνει χωρίς επαναλαμβανόμενες ακμές. Κάθε μονοπάτι που τις ενώνει
και έχει μήκος
τότε
υπάρχει ένα μονοπάτι που τις ενώνει χωρίς επαναλαμβανόμενες ακμές. Κάθε μονοπάτι που τις ενώνει
και έχει μήκος ![]() είναι τέτοιο (αλλιώς η απόστασή τους θα ήταν μικρότερη).
είναι τέτοιο (αλλιώς η απόστασή τους θα ήταν μικρότερη).
Υπόδειξη: Δύο κάτοικοι συνδέονται μεταξύ τους με ακμή αν και μόνο αν μπορούμε να αλλάξουμε το όνομα του ενός
σε ακριβώς μια θέση και να πάρουμε το όνομα του άλλου. Σκεφτόμενοι έτσι βλέπουμε ότι το να διασχίσουμε
μια ακμή στο γράφημα ισοδυναμεί με το να αλλάξουμε το όνομα της τρέχουσας κορυφής σε μια ακριβώς θέση.
Άρα το ερώτημα «ποια είναι η διάμετρος του ![]() » ισοδυναμεί με το ερώτημα «πόσες το πολύ αλλαγές πρέπει να κάνουμε στο όνομα ενός κατοίκου για να πάρουμε το όνομα ενός άλλου κατοίκου;»
» ισοδυναμεί με το ερώτημα «πόσες το πολύ αλλαγές πρέπει να κάνουμε στο όνομα ενός κατοίκου για να πάρουμε το όνομα ενός άλλου κατοίκου;»
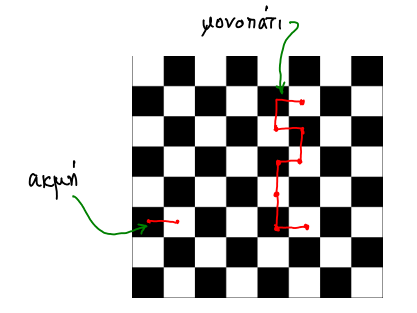
Υπόδειξη: Ας είναι ![]() δύο κορυφές του γραφήματος
δύο κορυφές του γραφήματος ![]() με
με
![]() .
Δείξτε ότι κάθε μια από τις
.
Δείξτε ότι κάθε μια από τις ![]() μπορεί να παίξει το ρόλο της προς διαγραφή κορυφής της Άσκησης.
μπορεί να παίξει το ρόλο της προς διαγραφή κορυφής της Άσκησης.
Υπόδειξη: Δείτε την Άσκηση 5.6.
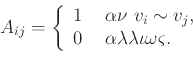
Με επαγωγή ως πρός ![]() δείξετε ότι
Ο πίνακας
δείξετε ότι
Ο πίνακας ![]() .
.![]() , (γινόμενο του πίνακα
, (γινόμενο του πίνακα ![]() με τον εαυτό
του
με τον εαυτό
του ![]() φορές) έχει στη θέση
φορές) έχει στη θέση ![]() τον αριθμό
τον αριθμό ![]() αν
και μόνο αν ο αριθμός των μονοπατιών μήκους
αν
και μόνο αν ο αριθμός των μονοπατιών μήκους ![]() από την κορυφή
από την κορυφή ![]() στην
στην
![]() είναι ακριβώς
είναι ακριβώς ![]() .
(Παρατήρηση: Ενα μονοπάτι μήκους
.
(Παρατήρηση: Ενα μονοπάτι μήκους ![]() από το
από το ![]() στο
στο ![]() μπορεί
να επαναλαμβάνει ακμές. Για παράδειγμα, αν
μπορεί
να επαναλαμβάνει ακμές. Για παράδειγμα, αν
![]() , τότε
το μονοπάτι
, τότε
το μονοπάτι
![]() είναι ένα μονοπάτι
από το
είναι ένα μονοπάτι
από το ![]() στο
στο ![]() μήκους
μήκους ![]() .)
.)
Υπόδειξη:
Αν ![]() είναι
είναι
![]() πίνακες και
πίνακες και ![]() είναι το γινόμενό τους (επίσης
είναι το γινόμενό τους (επίσης
![]() πίνακας) τότε εξ ορισμού
πίνακας) τότε εξ ορισμού
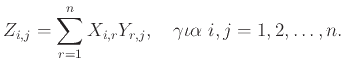
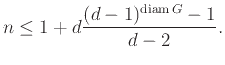
Υπόδειξη: Έστω ![]() μια κορυφή του
μια κορυφή του ![]() . Τα σύνολα κορυφών
. Τα σύνολα κορυφών
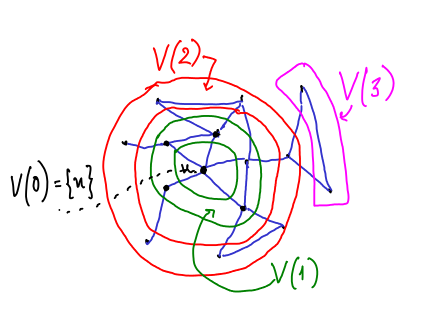
Mihalis Kolountzakis 2015-11-28