Next: 5.3 Υπογραφήματα και ισομορφία Up: 5. Εισαγωγή στη θεωρία Previous: 5.1 Απλά γραφήματα Contents Index
Το κενό γράφημα με ![]() κορυφές έχει σύνολο κορυφών
κορυφές έχει σύνολο κορυφών
![]() και σύνολο ακμών
και σύνολο ακμών
![]() .
Το συμβολίζουμε με
.
Το συμβολίζουμε με ![]() .
.
Το πλήρες γράφημα με ![]() κορυφές έχει σύνολο κορυφών
κορυφές έχει σύνολο κορυφών
![]() και όλες τις δυνατές ακμές, δηλ.
και όλες τις δυνατές ακμές, δηλ. ![]() = όλα τα διμελή
υποσύνολα του
= όλα τα διμελή
υποσύνολα του ![]() . Συμβολίζεται με
. Συμβολίζεται με ![]() και έχει
και έχει
![]() ακμές. Το αριστερό γράφημα στο Σχ. 5.10
είναι το
ακμές. Το αριστερό γράφημα στο Σχ. 5.10
είναι το ![]() .
.
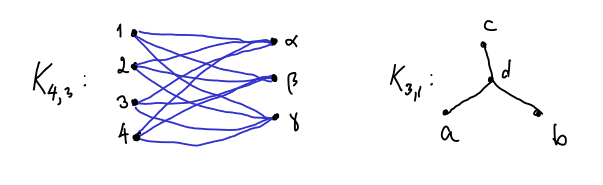
Το πλήρες διμερές γράφημα με ![]() και
και ![]() κορυφές έχει
σύνολο κορυφών το
κορυφές έχει
σύνολο κορυφών το
![]() , με
, με
![]() ,
,
![]() , και
, και
![]() , για κάθε
, για κάθε
![]() ,
,
![]() . Συμβολίζεται με
. Συμβολίζεται με ![]() και
έχει
και
έχει ![]() ακμές. Δείτε το Σχήμα 5.8 για παράδειγμα.
ακμές. Δείτε το Σχήμα 5.8 για παράδειγμα.
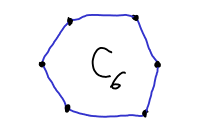
Ο κύκλος με ![]() κορυφές έχει σύνολο κορυφών το
κορυφές έχει σύνολο κορυφών το ![]() και
και ![]() αν και μόνο αν
αν και μόνο αν
![]() ή
ή
![]() .
Συμβολίζεται με
.
Συμβολίζεται με ![]() και έχει
και έχει ![]() ακμές.
Δείτε το Σχήμα 5.9 για παράδειγμα.
ακμές.
Δείτε το Σχήμα 5.9 για παράδειγμα.