6.1 Διμερή γραφήματα

Η κλάση των διμερών γραφημάτων κωδικοποιεί φυσιολογικά σχέσεις ανάμεσα σε δύο διαφορετικούς πληθυσμούς. Για παράδειγμα ας υποθέσουμε ότι έχουμε δύο ξένα πεπερασμένα σύνολα: το $A$, που είναι ένα σύνολο δασκάλων, και το $B$, που είναι ένα σύνολο μαθητών. Ορίζουμε ένα γράφημα με σύνολο κορυφών το $V=A \cup B$ το οποίο θα κωδικοποιεί τη σχέση διδασκαλίας, βάζουμε δηλ. μια ακμή ανάμεσα σε δύο κορυφές $u, v \in V$ αν και μόνο αν το $u$ διδάσκει το $v$ ή αντίστροφα. Είναι φανερό ότι όλες οι ακμές στο γράφημα αυτό συνδέουν μεταξύ τους μια κορυφή του $A$ και μια του $B$. Δεν υπάρχουν δηλ. ακμές που να συνδέουν ανάμεσά τους δύο κορυφές του $A$ ή δύο του $B$. Μία άλλη περίπτωση, αρκετά κοινή στην πράξη, είναι αυτή όπου έχουμε ένα γράφημα που περιγράφει τη σχέση ανάμεσα σε εξυπηρετητές (servers) και εξυπηρετούμενους (clients).

Ορισμός 6.1   (Διμερές γράφημα) Ενα γράφημα $G=(V,E)$ θα ονομάζεται διμερές αν υπάρχει μια διαμέριση των κορυφών

$$V = A \cup B, \mu\epsilon A \cap B = \emptyset,$$

τέτοια ώστε οι γείτονες κάθε κορυφής του $A$ ανήκουν στο $B$ (το οποίο συνεπάγεται ότι και οι γείτονες κάθε κορυφής του $B$ ανήκουν στο $A$). Δεν υπάρχουν δηλ. ακμές από το $A$ στο $A$ ή από το $B$ στο $B$.

Παράδειγμα 6.1   Σε ένα σύνολο ανθρώπων η σχέση του γάμου ορίζει ένα διμερές γράφημα. Αν έχουμε δηλ. ένα γράφημα με σύνολο κορυφών $V$ κάποιο σύνολο ανθρώπων, και βάλουμε μια ακμή ανάμεσα σε δύο κορυφές αν αυτές αντιπροσωπεύουν συζύγους, τότε το γράφημα είναι διμερές με σύνολο κορυφών $A$ το σύνολο των γυναικών και σύνολο κορυφών $B$ το σύνολο των ανδρών.

Σχήμα 6.1: Ένα διμερές γράφημα, σχεδιασμένο με δύο τρόπους

Παρατήρηση 6.1   Τα διμερή γραφήματα τα σχεδιάζουμε συνήθως (αλλά όχι πάντα) με τις δύο ομάδες ($A$ και $B$) των κορυφών τους σαφώς χωρισμένες, συνήθως σε αριστερά και δεξιά. Για παράδειγμα, το γράφημα στο Σχ. 6.1(a) είναι διμερές με

$$A = {\left\{{1,3,6}\right\}}, B={\left\{{2,4,5,7}\right\}}.$$

Δεν είναι πάντα προφανές, απλά κοιτώντας ένα γράφημα, αν είναι αυτό διμερές ή όχι. Το γράφημα στο Σχ. 6.1(b) είναι το ίδιο με το γράφημα στο (a) αλλά πρέπει κανείς να σκεφτεί για να δεί ότι όντως είναι διμερές.

Παρατήρηση 6.2   Παρατηρήστε ότι η διαμέριση $V=A \cup B$ δεν είναι μοναδική, μια και θα μπορούσαμε να είχαμε τοποθετήσει, για παράδειγμα, το $1$ στο σύνολο $B$ αντί για το $A$.

Άσκηση 6.1   Δείξτε ότι ένα γράφημα $G$ είναι διμερές αν και μόνο αν κάθε συνεκτική συνιστώσα του $G$ είναι διμερές γράφημα.

Άσκηση 6.2   Βρείτε μια μέθοδο για να αποφασίζετε αν ένα τυχόν απλό γράφημα είναι διμερές ή όχι.

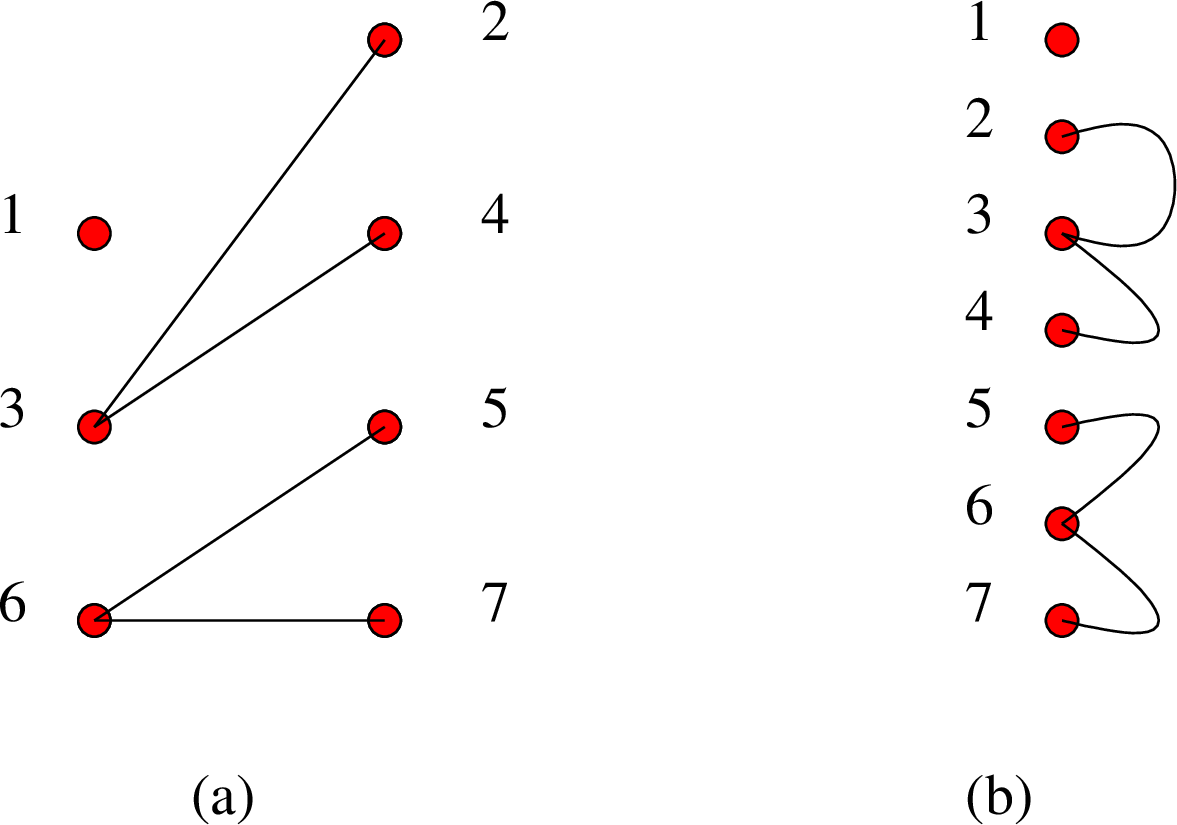
Υπόδειξη: Κατ' αρχήν, αρκεί να βρούμε μια τέτοια μέθοδο που δουλεύει για συνεκτικά γραφήματα (σύμφωνα με την Άσκηση 6.1). Για ένα συνεκτικό γράφημα $G=(V,E)$ επιλέγουμε αυθαίρετα μια κορυφή του $u$ και ορίζουμε τα σύνολα

$$V(k) = {\left\{{v\in V: d(u,v)=k}\right\}}, k=0,1,\ldots,{\rm diam }G,$$

τα οποία διαμερίζουν το σύνολο κορυφών $V$. Το σύνολο $V(k)$ απαρτίζεται από εκείνες τις κορυφές του $G$ που απέχουν απόσταση ακριβώς $k$ από την κορυφή $u$. Δείξτε ότι το $G$ είναι διμερές αν και μόνο αν για κάθε ακμή

$$ab, \mu\epsilon a \in V(i), b \in V(j),$$

έχουμε $i \equiv j$ mod 2, είναι δηλ. τα $i,j$ είτε και τα δύο άρτια είτε και τα δύο περιττά.

Θεώρημα 6.1   Όλα τα δέντρα είναι διμερή γραφήματα.

Απόδειξη. Η απόδειξη είναι με επαγωγή ως προς το $n = {\left\vert{V}\right\vert}$. Αν $n=1$, τότε το μοναδικό δέντρο είναι αυτό με μια κορυφή $u$ και καμιά ακμή. Ορίζουμε τότε το διαμερισμό του συνόλου $V = {\left\{{u}\right\}}$ στα σύνολα $A={\left\{{u}\right\}}$ και $B = \emptyset$.

Για το επαγωγικό βήμα, υποθέτουμε ότι η πρόταση ισχύει αν το δέντρο έχει το πολύ $n-1$ κορυφές και παίρνουμε ένα δέντρο $T$ με $n$ κορυφές. Θέλουμε να δείξουμε ότι είναι διμερές. Γνωρίζουμε όμως (δείτε τον ισχυρισμό μέσα στην απόδειξη του Θεωρήματος 5.2) ότι κάθε δέντρο έχει μια κορυφή βαθμού 1. Έστω $u$ μια τέτοια κορυφή του δέντρου $T$, και $v$ ο μοναδικός γείτονάς της. Αν από το $T$ αφαιρέσουμε την κορυφή $u$ και την ακμή $uv$, τότε το γράφημα που προκύπτει, έστω $T'$ είναι και πάλι δέντρο (αφού εξακολουθεί να παραμένει συνεκτικό γράφημα, χωρίς κύκλους) με $n-1$ κορυφές. Από την επαγωγική μας υπόθεση έπεται ότι το $T'$ είναι διμερές με σύνολα κορυφών τα $A'$ και $B'$ (όλες οι ακμές του $T'$ δηλ. πάνε από το $A'$ στο $B'$). Η κορυφή $v$ ανήκει σε ένα από τα δύο αυτά σύνολα, έστω στο $A'$.

Ισχυριζόμαστε τώρα ότι το δέντρο $T$ είναι διμερές γράφημα με σύνολα κορυφών τα $A = A'$ και $B = B' \cup {\left\{{u}\right\}}$. Για να το ελέγξουμε αυτό, και εφόσον γνωρίζουμε ότι δεν υπάρχουν ακμές από το $A'$ στο $B'$, αρκεί να ελέγκσουμε ότι δεν υπάρχουν ακμές από το $u$ προς κάποια κορυφή του $B'$. Αυτό όμως είναι προφανές αφού το $u$ έχει μόνο ένα γείτονα, το $v$, ο οποίος είναι στο $A$. $\qedsymbol$

Σχήμα 6.2: Ένας τρόπος να βρούμε τα δύο σύνολα $A$ και $B$ που ορίζουν ένα δέντρο ως διμερές γράφημα είναι να ξεκινήσουμε από μια αυθαίρετη κορυφή $u$ του δέντρου την οποία και χρωματίζουμε κόκκινη, μετά να χρωματίσουμε τους γείτονές της πράσινους, μετά να χρωματίσουμε τους αχρωμάτιστους γείτονες των τελευταίων κορυφών που χρωματίσαμε με το άλλο χρώμα κλπ.

Άσκηση 6.3   Αν ένα γράφημα είναι διμερές τότε και κάθε υπογράφημά του είναι.

Άσκηση 6.4   Ο κύκλος $C_n$ είναι το γράφημα με σύνολο κορυφών το ${\left\{{1,2,\ldots,n}\right\}}$ και σύνολο ακμών το

$$E = {\left\{{(1,2), (2,3), \ldots, (n-1,n), (n,1)}\right\}}.$$

Δείξτε ότι το $C_n$ είναι διμερές γράφημα αν και μόνο αν το $n$ είναι άρτιο.

Άσκηση 6.5   Το πλήρες διμερές γράφημα με $m$ και $n$ κορυφές, που το συμβολίζουμε με $K_{mn}$ είναι ένα διμερές γράφημα με σύνολα κορυφών $A={\left\{{a_1,\ldots,a_m}\right\}}$ και $B={\left\{{b_1,\ldots,b_n}\right\}}$, όπου το σύνολο των ακμών είναι το μέγιστο δυνατό.

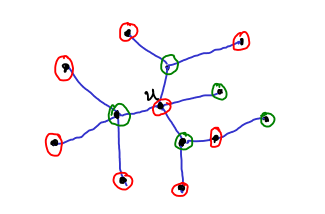
Δείτε στο Σχήμα 5.8 π.χ. το γράφημα $K_{4,3}$.

1. Πόσες ακμές έχει το $K_{mn}$;
2. Για ποιες τιμές των $m$ και $n$ είναι το $K_{mn}$ κανονικό; (Θυμίζουμε ότι ένα γράφημα λέγεται κανονικό αν όλες οι κορυφές του έχουν τον ίδιο βαθμό.)
3. Περιγράψτε το συμπληρωματικό γράφημα του $K_{mn}$. (Συμπληρωματικό ενός γραφήματος $G$ είναι το γράφημα $G'$ με ίδιο σύνολο κορυφών και τέτοιο ώστε μια ακμή υπάρχει στο $G'$ αν και μόνο αν δεν υπάρχει στο $G$.) Είναι αυτό διμερές;

Άσκηση 6.6   Μπορεί ένα δέντρο να είναι πλήρες διμερές γράφημα; (Δείτε ορισμό στην Άσκηση 6.5.)

Τα διμερή γραφήματα χαρακτηρίζονται από τα μήκη των κυκλωμάτων τους:

Θεώρημα 6.2   Ένα γράφημα είναι διμερές αν και μόνο αν όλα τα κυκλώματά του έχουν άρτιο μήκος.

Απόδειξη. Έστω $G$ διμερές γράφημα και $C$ κύκλωμα σε αυτό:

$$C: u_1 \to u_2 \to \cdots \to u_n \to u_1.$$

Το μήκος του $C$ είναι $n$ και θέλουμε να δείξουμε ότι αυτό είναι άρτιο. Μπορούμε να υποθέσουμε ότι το $u_1$ ανήκει στο σύνολο κορυφών $A$. Άρα το $u_2$ ανήκει στο σύνολο κορυφών $B$, το $u_3$ ανήκει πάλι στο $A$, κλπ. Δηλ. τα $u_j$ με άρτιο $j$ ανήκουν στο $B$ και αυτά με περιττό $j$ στο $A$. Όμως το $u_n$ είναι γείτονας του $u_1$, άρα ανήκει στο $B$, το οποίο συνεπάγεται ότι το $n$ είναι άρτιο.

Αντίστροφα, έστω $G$ ένα γράφημα, με σύνολο κορυφών $V$, στο οποίο όλα τα κυκλώματα έχουν άρτιο μήκος. Υποθέτουμε πρώτα ότι το $G$ είναι συνεκτικό και σταθεροποιούμε μια κορυφή του $u$. Ορίζουμε

$$A = {\left\{{v \in V: d(u,v) \alpha\rho\tau\iota o}\right\}}$$

και

$$B = V \setminus A.$$

Δείχνουμε ότι το $G$ είναι διμερές με σύνολα κορυφών τα $A$ και $B$. Γι' αυτό αρκεί να δείξουμε ότι είναι αδύνατο να υπάρχει ακμή ανάμεσα σε δύο κορυφές του $A$ ή ανάμεσα σε δύο κορυφές του $B$. Έστω $a_1$ και $a_2$ δύο κορυφές του $A$ (επιχειρηματολογούμε τελείως όμοια για δύο κορυφές του $B$) και ας υποθέσουμε, αντίθετα με αυτό που θέλουμε να αποδείξουμε, ότι υπάρχει στο $G$ η ακμή $a_1a_2$. Έστω $\pi_1$ και $\pi_2$ δύο ελάχιστα μονοπάτια στο $G$ από την $u$ στις κορυφές $a_1$ και $a_2$. Θεωρούμε τον κύκλο $C$ που απαρτίζεται από το $\pi_1$ ακολουθούμενο από την ακμή $a_1a_2$ και τέλος από το $\pi_2$ διανυμένο με ανάποδη σειρά. Το μήκος του $C$ είναι

$${\left\vert{C}\right\vert} = {\left\vert{\pi_1}\right\vert} + 1 + {\left\vert{\pi_2}\right\vert},$$

που είναι φανερό ότι είναι περιττός αριθμός, πράγμα άτοπο.

Έχουμε λοιπόν δείξει τη συνεπαγωγή «άρτια κυκλώματα συνεπάγεται διμερές γράφημα» στην περίπτωση που το $G$ είναι συνεκτικό. Αν το $G$ δεν είναι συνεκτικό παρατηρούμε ότι κάθε συνεκτική συνιστώσα του είναι διμερής, άρα και το ίδιο το $G$ (δείτε Άσκηση 6.1). $\qedsymbol$

Άσκηση 6.7   Ο χρωματικός αριθμός ενός γραφήματος $G$, που συμβολίζεται με $\chi(G)$, είναι ο ελάχιστος ακέραιος $k$ τέτοιος ώστε να μπορεί κανείς με $k$ διαφορετικά χρώματα να χρωματίσει τις κορυφές του $G$, με τέτοιο τρόπο ώστε αν δύο κορυφές συνδέονται με ακμή τότε να έχουν διαφορετικά χρώματα. Για παράδειγμα ο χρωματικός αριθμός ενός τριγώνου ($K_3$) είναι 3. Δείξτε ότι ένα γράφημα $G$ είναι διμερές αν και μόνο αν $\chi(G)\le 2$.

Άσκηση 6.8   Αν $A={\left\{{a_1,\ldots,a_m}\right\}}$ και $B={\left\{{b_1,\ldots,b_n}\right\}}$, πόσα διμερή γραφήματα υπάρχουν με σύνολα κορυφών τα $A$ και $B$;

Υπόδειξη: Κάθε μια από τις δυνατές ακμές από το $A$ στο $B$ μπορεί να επιλεγεί ως ακμή ή όχι.

Άσκηση 6.9   Αν $A={\left\{{a_1,\ldots,a_m}\right\}}$ και $B={\left\{{b_1,\ldots,b_n}\right\}}$, για ποιες τιμές των $m, n$ και $r$ υπάρχει $r$-κανονικό γράφημα με σύνολα κορυφών τα $A$ και $B$;

Υπόδειξη: Μετρήστε κατ' αρχήν τις ακμές ενός τέτοιου γραφήματος από τη μεριά του $A$. Αφού για κάυε κορυφή του $A$ έχουμε $r$ ακμές που φεύγουν από αυτό θα έχει συνολικά $m\cdot r$ ακμές ένα τέτοιο γράφημα. Κάντε το ίδιο από την πλευρά του $B$.

Για την αντίστροφη κατεύθυνση θα πρέπει να δώσετε μια κατασκευή.

Άσκηση 6.10   Τι μορφή έχει ο πίνακας συνδεσμολογίας ενός διμερούς γραφήματος (μετά από κατάλληλη αρίθμηση των κορυφών του);