Περιεχόμενα - Εισαγωγή στη Θεωρία Ομάδων

Κεφάλαιο 3Ομάδα πηλίκο - Θεωρήματα ισομορφίας

Στο κεφάλαιο αυτό θα αποδείξουμε το θεώρημα του Lagrange, το οποίο για τις πεπερασμένες ομάδες διατυπώνεται ως εξής: η τάξη κάθε υποομάδας μίας ομάδας διαιρεί την τάξη της ομάδας. Ένα εξαιρετικό συμπέρασμα που μας επιτρέπει να ξεκινήσουμε τη μελέτη των υποομάδων μίας ομάδας. Θα οδηγηθούμε στο συμπέρασμα του Lagrange μετά από μία κατασκευή, η οποία θα ορίσει την ομάδα πηλίκο. Μία ομάδα που κατασκευάζεται με την βοήθεια μίας υποομάδας και της ίδιας της ομάδας. Η ομάδα πηλίκο θα μας θυμίσει το πηλίκο στους αριθμούς κυρίως λόγω των ιδιοτήτων της.

Η προσπάθεια να συγκριθούν μεταξύ τους ομάδες οι οποίες δεν φαίνεται να έχουν κάποια σχέση μεταξύ τους, προκειμένου να πλησιάσουμε τα μεγάλα προβλήματα ταξινόμησης, έχει ένα πρώτο σταθμό τα θεωρήματα ισομορφίας ομάδων. Τα θεωρήματα ισομορφίας αποτελούν τη δεύτερη ενότητα αυτού του κεφαλαίου.

3.1 Δείκτης υποομάδας - Θεώρημα Lagrange

Θεωρούμε μία ομάδα G και Α,Β δύο υποσύνολα της G. Ορίζουμε το γινόμενο των Α,Β ως εξής:

A⁢B:={α⁢β:α∈A,β∈B}. (3.1)

Είναι φανερό ότι A⁢B⊆G. Ιδιαίτερα αν A={α}, τότε γράφουμε α⁢B:={α}⁢B. Η επόμενη πρόταση συγκεντρώνει τις κυριότερες ιδιότητες του γινομένου υποσυνόλων ομάδων.

Πρόταση 3.1.1

Έστω Α,Β,Γ υποσύνολα μιας ομάδας G. Τότε:

  1. i.

    A⁢(B⁢Γ)=(A⁢B)⁢Γ.

  2. ii.

    A⁢(B∪Γ)=A⁢B∪A⁢Γ,(A∪B)⁢Γ=A⁢Γ∪B⁢Γ.

  3. iii.

    A⁢(B∩Γ)⊆A⁢B∩A⁢Γ,(A∩B)⁢Γ⊆A⁢Γ∩B⁢Γ.

  4. iv.

    (A⁢B)-1=B-1⁢A-1, όπου X-1={x-1:x∈X}.

  5. v.

    Αν η πράξη της G ορίζεται στο υποσύνολο Α, τότε A2⊆A. Ιδιαίτερα, αν e∈A, τότε A2=A.

Η απόδειξη αφήνεται ως άσκηση για τον αναγνώστη.

Από την Πρόταση 3.1.1 προκύτει ότι το δυναμοσύνολο P⁢(G):={A:A⊆G} του συνόλου G με πράξη τον πολλαπλασιασμό υποσυνόλων του G είναι μονοειδές. Όμως, δεν είναι ομάδα, όπως διαπιστώνουμε με το ακόλουθο παράδειγμα. Θεωρούμε την ομάδα S3 και το σύνολο {A,B,Γ} υποσυνόλων της S3, όπου

Α={(123213),(123321)},B={(123213),(123132)},Γ={(123321),(123132)}. (3.2)

Παρατηρούμε ότι, ενώ ΑΒ=ΑΓ, δεν έπεται ότι Β=Γ. Ο ορισμός του γινομένου υποσυνόλων ομάδας μας οδηγεί στο ερώτημα μήπως το γινόμενο υποομάδων μίας ομάδας είναι ομάδα. Η απάντηση δεν είναι πάντα καταφατική όπως φαίνεται από την επόμενη πρόταση.

Πρόταση 3.1.2

Έστω G μία ομάδα και H,K≤G. Τότε H⁢K≤G αν και μόνον αν H⁢K=K⁢H.

(Ας παρατηρήσουμε στο σημείο αυτό ότι η σχέση H⁢K=K⁢H δεν σημαίνει ότι τα στοιχεία της Η και τα στοιχεία της Κ αντιμεταθέτονται, αλλά ότι κάθε στοιχείο του συνόλου ΗΚ ανήκει στο σύνολο ΚΗ και αντίστροφα.)

Απόδειξη: Ας υποθέσουμε ότι H⁢K≤G. Τότε από την Πρόταση 1.2.5, i) και την Πρόταση 3.1.1,iv), έχουμε H⁢K=(H⁢K)-1=K-1⁢H-1=K⁢H. Αντίστροφα, τώρα, έστω ότι για τις υποομάδες Η και Κ της ομάδας G ισχύει ότι ΗΚ=ΚΗ. Θα εφαρμόσουμε το κριτήριο της υποομάδας για να αποδείξουμε ότι H⁢K≤G. Έστω α,β∈H⁢K, τότε α=h1⁢k1 και β=h2⁢k2, για κάποια στοιχεία h1,h2∈H και k1,k2∈K. Ακόμη α⁢β-1=h1⁢k1⁢k2-1⁢h2-1 ,όμως, το στοιχείο k1⁢k2-1∈K, αφού K≤G και το στοιχείο k1⁢k2-1⁢h2-1∈K⁢H=H⁢K. Άρα υπάρχουν στοιχεία h3∈H και k3∈K, ώστε k1-1⁢k2-1⁢h2-1=h3⁢k3. Επομένως α⁢β-1=h1⁢h3⁢k3∈H⁢K, δηλ. Η⁢Κ≤G. ■

Παράδειγμα 3.1.3

Θεωρούμε την ομάδα S3 και έστω σ=(123231) και τ=(123213). Παρατηρούμε ότι

<σ>⁢<σ⁢τ>≠<σ⁢τ>⁢<σ>. (3.3)

Επομένως το γινόμενο <σ>⁢<σ⁢τ> δεν είναι υποομάδα της S3, ενώ

<σ><τ≥<τ><σ≥S3. (3.4)

Ορίζουμε, τώρα, μία σχέση ισοδυναμίας στο σύνολο της ομάδας G που θα οδηγήσει στο θεώρημα του Lagrange. Σχετικά με τις σχέσεις ισοδυναμίας ο αναγνώστης παραπέμπεται στο Παράρτημα Α.

Πρόταση 3.1.4

Έστω G μία ομάδα και H≤G.

  1. (i)

    Η σχέση β∼α⇔β⁢α-1∈H, για α,β∈G, είναι σχέση ισοδυναμίας στο σύνολο G. Η κλάση α¯ του στοιχείου α είναι το σύνολο H⁢α,

    G=⊍α∈GHα και G/∼={Hα:α∈G}. 3.1.1
  2. (ii)

    Η σχέση β∼α⇔α-1⁢β∈H, για α,β∈G, είναι σχέση ισοδυναμίας στο σύνολο G. Η κλάση α¯ του στοιχείου α είναι το σύνολο α⁢H,

    G=⊍α∈GαH και G/∼={αH:α∈G}. 3.1.2

Απόδειξη: i. Για α=β, ισχύει ότι α⁢α-1=e∈H, για κάθε α∈G, δηλ.

α∼α,∀α∈G. (3.5)

Άρα η σχέση "∼" είναι ανακλαστική.
Αν β∼α, για α,β∈G, τότε

β⁢α-1∈H⇒(β⁢α-1)-1∈H⇒α⁢β-1∈H⇒α∼β, (3.6)

δηλ. η σχέση "∼" είναι συμμετρική.
Αν α,β,γ∈G και β∼α,α∼γ, τότε

β⁢α-1∈H⁢ και ⁢α⁢γ-1∈H⇒ (3.7)
⇒βα-1αγ-1∈H⇒βγ-1∈H⇒β∼γ, (3.8)

δηλ. η σχέση "∼" είναι μεταβατική.
Από τον ορισμό της "∼" έπεται ότι β∼α⇔β⁢α-1∈H⇔β∈H⁢α. Επομένως η κλάση α¯ του στοιχείου α είναι το σύνολο H⁢α,α∈G. ’Αρα

G=⊍α∈GHα και G/∼={Hα:α∈G}. (3.9)

ii. Όμοια με το i. η σχέση "∼" είναι σχέση ισοδυναμίας που χωρίζει το σύνολο G στις κλάσεις α¯=α⁢H για α∈G. ’Αρα

G=⊍α∈GαH και G/∼={αH:α∈G}.■ (3.10)
Ορισμός 3.1.5

Έστω G μία ομάδα και H≤G. Η κλάση H⁢α,α∈G, λέγεται δεξιά κλάση (right coset) της Η στη G με αντιπρόσωπο το α. Η κλάση α⁢H λέγεται αριστερή κλάση (left coset) της Η στη G με αντιπρόσωπο το α.

Συμβολισμός: Το σύνολο πηλίκο G/∼ ως προς τη σχέση ισοδυναμίας όπως αυτή αναφέρεται στο i) της Πρότασης 3.1.4 καθώς και ως προς τη σχέση ισοδυναμίας ii) της ίδιας πρότασης θα συμβολίζεται στο εξής ως G/H και θα αναφέρεται σαφώς στο κείμενο αν πρόκειται για τις αριστερές ή τις δεξιές κλάσεις.

Ας θεωρήσουμε την ανάλυση της G όπως στη σχέση 3.1.1. Αν H={e}, τότε είναι φανερό ότι κάθε στοιχείο της ομάδας είναι αντιπρόσωπος μιας κλάσης η οποία περιέχει ένα ακριβώς στοιχείο. Ενώ αν H=G, τότε υπάρχει μία μόνον κλάση η ίδια η G. Μπορούμε, λοιπόν, να γράψουμε τη σχέση 3.1.1 ως εξής:

G=⊍α∈I⁢H⁢α, 3.1.3

όπου Ι είναι ένα πλήρες σύστημα αντιπροσώπων των δεξιών κλάσεων, δηλαδή ένα σύνολο που περιέχει ένα ακριβώς στοιχείο από κάθε δεξιά κλάση. Τότε το σύνολο πηλίκo G/H έχει την ισχύ του συνόλου Ι. Όμοια για την ανάλυση της G σε αριστερές κλάσεις

G=⊍α∈J⁢α⁢H, 3.1.4

όπου J είναι ένα πλήρες σύνολο αντιπροσώπων των αριστερών κλάσεων.

Πρόταση 3.1.6

Έστω G μία ομάδα και H≤G. Τότε το σύνολο των αριστερών κλάσεων της Η στην G έχει την ίδια ισχύ με το σύνολο των δεξιών κλάσεων της Η στην G, δηλ. |I|=|J|, όπως τα Ι και J ορίζονται στις σχέσεις (3.1.3) και (3.1.4). Ακόμη τα σύνολα Ι και J μπορούν να επιλεγούν ώστε J=I-1.

Απόδειξη: Έστω H⁢α,α∈G μία δεξιά κλάση της Η στη G. Είναι φανερό ότι η α-1⁢H είναι μία αριστερή κλάση της Η στη G. Θεωρούμε την αντιστοιχία

f:{H⁢α:α∈I}⟶{β⁢H:β∈J},H⁢α↦α-1⁢H. (3.11)

Θα αποδείξουμε ότι η f είναι μία αμφιμονότιμη και επί συνάρτηση. Έστω α1,α2∈G, τότε

H⁢α1=H⁢α2⇔H⁢α1⁢α2-1=H⇔α1⁢α2-1∈H⇒α2-1∈α1-1⁢H⇒α2-1⁢H=α1-1⁢H. (3.12)

Άρα η f είναι αμφιμονότιμη συνάρτηση. Τώρα, αν β∈G και β⁢H είναι μία αριστερή κλάση, τότε υπάρχει η δεξιά κλάση H⁢β-1 ώστε f⁢(H⁢β-1)=β⁢H, δηλ. η f είναι επί συνάρτηση. Επομένως, η f είναι αμφιμονότιμη και επί συνάρτηση, δηλ. |I|=|J|. Ισοδύναμα |{H⁢α:α∈I}|=|{β⁢H:β∈J}|. Τέλος από τη συνάρτηση f έπεται ότι δοθέντος του συνόλου Ι, μπορούμε να επιλέξουμε ως J το σύνολο I-1 και ισοδύναμα δοθέντος του J, τότε μπορούμε να επιλέξουμε ως Ι το J-1. ■

Ορισμός 3.1.7

Έστω G μία ομάδα και H≤G. Το πλήθος των αριστερών (άρα και των δεξιών) κλάσεων της Η στη G λέγεται  δείκτης (index) της Η στη G και συμβολίζεται [G:H].

Παραδείγματα 3.1.8

1. Θεωρούμε την ομάδα (ℤ,+) και την υποομάδα της n⁢ℤ. Έστω α∈ℤ, τότε

α¯={β∈ℤ:β∼α}={β∈ℤ:β-α∈n⁢ℤ}={β∈ℤ:β∈α+n⁢ℤ}. (3.13)

Με άλλα λόγια στην κλάση του α βρίσκονται όλοι οι ακέραιοι οι οποίοι διαιρούμενοι δια του n αφήνουν υπόλοιπο α και επειδή τα δυνατά υπόλοιπα της διαίρεσης δια του n είναι: 0,1,…,n-1, προκύπτει ότι

ℤ/n⁢ℤ={0¯,1¯,2¯,…,n-1¯}. (3.14)

Άρα [ℤ:nℤ]=n. Ακόμη βλέπουμε ότι ℤ/n⁢ℤ=ℤn (βλ. Παράδεγμα 1.1.2.8). Από το Παράδειγμα αυτό διαπιστώνουμε ότι οι ισοδυναμίες (3.1.1) και (3.1.2) είναι γενικεύσεις σε μία τυχαία ομάδα G της ισοδυναμίας με την οποία ορίστηκε το σύνολο ℤn.
2. Θεωρούμε την ομάδα S3 και έστω σ=(123231),τ=(123213) όπως στο Παράδειγμα 2.1.15.1. Αν H=<σ> τότε

S3=H⁢⊍⁢x⁢H, (3.15)

αφού 3=|H|=|x⁢H| και |S3|=6. Ως στοιχείο x μπορεί να είναι κάθε στοιχείο που ανήκει στην ομάδα S3 και δεν ανήκει στην ομάδα Η. Άρα

S3=H∪τ⁢H,S3=H∪σ⁢τ⁢H,S3=H∪σ2⁢τ⁢H. (3.16)

Ακόμη, αφού τ-1=τ,(σ⁢τ)-1=σ⁢τ και (σ2⁢τ)-1=σ2⁢τ, έχουμε

S3=H∪H⁢τ=H∪τ⁢H,S3=H∪H⁢σ⁢τ,S3=H∪H⁢σ2⁢τ. (3.17)

Αν, τώρα, λάβουμε την υποομάδα K=<τ>, τότε διαπιστώνουμε ότι

S3=K∪σ⁢K∪σ2⁢K⁢ και ⁢S3=K∪K⁢σ2∪K⁢σ, (3.18)

αφού σ-1=σ2.

Θεώρημα (Lagrange) 3.1.9

Έστω G μία πεπερασμένη ομάδα και H≤G. Τότε η τάξη της Η διαιρεί την τάξη της G.

Απόδειξη: Από τη σχέση 3.1.3 και την Πρόταση 3.1.6, εφόσον η G είναι πεπερασμένη προκύπτει ότι |G|=[G:H]|H|. Άρα η τάξη της Η διαιρεί την τάξη της G. ■

Μία πρώτη παρατήρηση από το Θεώρημα του Lagrange είναι ότι μπορούμε να αποκλείουμε πολλά υποσύνολα μίας πεπερασμένης ομάδας από το να είναι υποομάδες της. Έτσι οι υποομάδες της S3 μπορούν να έχουν τάξη 1, 2, 3 ή 6.

Ας παρατηρήσουμε ακόμη ότι το αντίστροφο του Θεωρήματος του Lagrange δεν ισχύει, δηλ. για κάθε m που διαιρεί την τάξη της ομάδας G, δεν έπεται ότι υπάρχει υποομάδα της G με τάξη m. Αυτό θα το δούμε στην Πρόταση 8.2.3.

Η επόμενη πρόταση είναι μία πολύ ενδιαφέρουσα συνέπεια του Θεωρήματος Lagrange.

Πρόταση 3.1.10

Έστω G μία πεπερασμένη ομάδα. Η τάξη κάθε στοιχείου της G διαιρεί την τάξη της G. Επιπλέον αn=e, όπου n=|G|.

Απόδειξη: Όπως είδαμε στο εδάφιο 2.2, κάθε στοιχείο g∈G δημιουργεί μία υποομάδα <g> της G και από την Πρόταση 2.2.2 i. έχουμε ότι |<g>|=o⁢r⁢d⁢(g). Από το θεώρημα του Lagrange έπεται ότι, αν |G|<∞,

ord(g)∣|G|.   ■ (3.19)
Πρόταση 3.1.11

Κάθε ομάδα τάξης πρώτου αριθμού είναι κυκλική με παράγον στοιχείο κάθε στοιχείο της g≠e.

Απόδειξη: Έστω G μία ομάδα με |G|=p, όπου p πρώτος φυσικός αριθμός και e≠α∈G. Τότε από την Πρόταση 3.1.10 org(α)∣|G|, δηλ. ord(α)∣p, άρα o⁢r⁢d⁢(α)=p. Αυτό σημαίνει ότι |<α>|=o⁢r⁢d⁢(α)=p (Βλ. Πρόταση 2.2.2, i. ). Επομένως η τάξη της υποομάδας <α> της G έχει την ίδια τάξη με την G, άρα <α≥G, για κάθε α∈G με α≠e. ■

Το επόμενο συμπέρασμα, που είναι επίσης συνέπεια του Θεωρήματος Lagrange, μας δίνει ουσιαστική πληροφορία για τη δομή των κυκλικών ομάδων.

Θεώρημα 3.1.12

Έστω G=<g> μία κυκλική ομάδα τάξης n<∞. Για κάθε φυσικό αριθμό s τέτοιον, ώστε s|n, υπάρχει μοναδική υποομάδα Η της G τάξης s και μάλιστα H=<gn/s>.

Απόδειξη: Έστω s ένας διαιρέτης του n, όπου n=o⁢r⁢d⁢(g) και G=<g>. Από την Πρόταση 2.2.5 γνωρίζουμε ότι

o⁢r⁢d⁢(gn/s)=n(n,ns)=s. (3.20)

Άρα

<gn/s>≤G⁢ και ⁢|<gn/s>|=s. (3.21)

Έστω τώρα, μία άλλη υποομάδα Η της G με τάξη s. Η υποομάδα Η οφείλει να είναι κυκλική (βλ. Θεώρημα 2.2.8). Έστω, λοιπόν, H=<gk>, όπου gk∈G με o⁢r⁢d⁢(gk)=s. Τότε από την Πρόταση 2.2.2, i⁢i⁢i. έχουμε

(gk)s=e⇒gk⁢s=e⇒n|ks⇒ks=nλ⇒k=nsλ, (3.22)

για κάποιο λ∈ℤ. Άρα (gn/s)λ∈<gn/s>, δηλ.

H=<gk>≤<gn/s>. 3.1.5

Όμως οι δύο ομάδες Η και <gn/s> έχουν τάξη ίση με s, έτσι από τη σχέση (3.1.5) έπεται ότι H=<gn/s>. Επομένως υπάρχει μοναδική υποομάδα τάξης s, η <gn/s>. ■

Παραδείγματα 3.1.13

1. Ομάδες τάξης 4. Ας υπολογίσουμε τις υποομάδες μίας ομάδας τάξης 4. Όπως είδαμε από το Παράδειγμα 1.2.8.1 οι ομάδες τάξης 4 περιγράφονται από τους Πίνακες 1.12 - 1.15. Είναι φανερό ότι οι ομάδες που έχουν πίνακα Cayley τον Πίνακα 2, 3 ή 4 είναι κυκλικές, άρα σύμφωνα με το Θεώρημα 2.3.11, ii) κάθε μία είναι ισόμορφη με την (ℤ4,+). Ας καλέσουμε K την ομάδα τάξης 4 με πίνακα Cayley τον Πίνακα 1, δηλ.

K:={e,α,β,α⁢β}, με ⁢α2=e=β2. (3.23)

Είναι φανερό ότι η K δεν είναι κυκλική και είναι αβελιανή. Οι ομάδες K και (ℤ4,+) δεν είναι ισόμορφες, αφού η ℤ4 έχει στοιχείο τάξης 4, ενώ η K δεν έχει (βλ.ακόμη άσκηση 2.3.14). Έτσι υπάρχουν δύο ακριβώς ομάδες τάξης 4: η ℤ4 και η K. Η ομάδα K λέγεται ομάδα του Klein προς τιμήν του Felix Klein. Καταλήγουμε έτσι στο συμπέρασμα:

Πρόταση 3.1.14

Υπάρχουν με προσέγγιση ισομορφίας δύο μόνον ομάδες τάξης 4: η κυκλική τάξης 4 και η ομάδα του Klein.

Από το Θεώρημα του Lagrange και το Θεώρημα 2.2.8 προκύπτει ότι υπάρχουν ακριβώς τρεις υποομάδες της ℤ4 οι: {0¯},{2¯},ℤ4=<1¯≥<3¯>. Το διάγραμμα των υποομάδων της ℤ4 είναι όπως στο Σχήμα 3.1

(3.24)
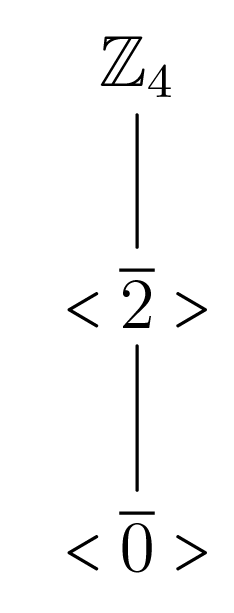Σχήμα 3.1

Ομοίως η G έχει τέσσερις υποομάδες τις: {e},<α>,<β>,<α⁢β> με διάγραμμα όπως στο Σχήμα 3.2

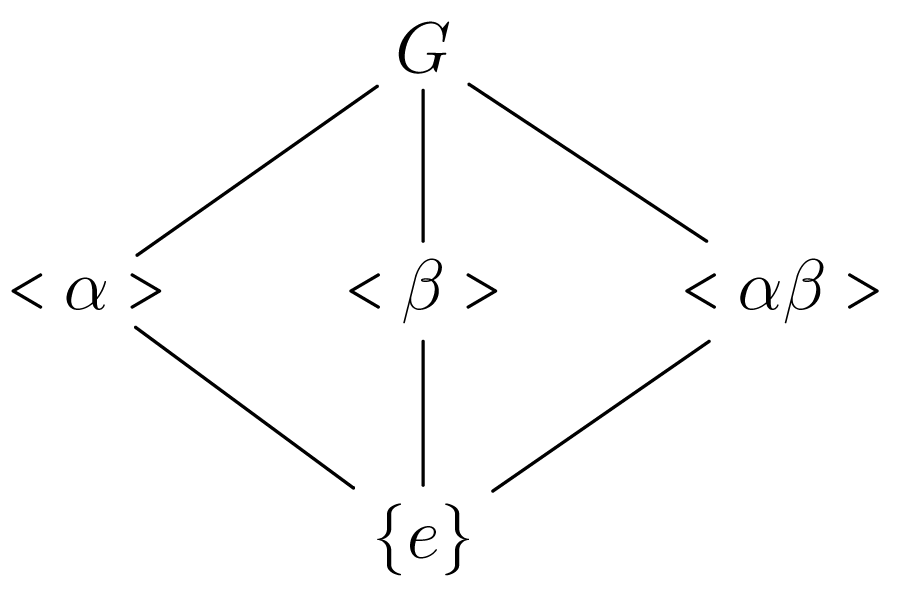Σχήμα 3.2

(βλ. Πρόταση (3.1.11) ).

2. Το διαγραμμα των υποομάδων της (S3,⋅). Από το Παράδειγμα 2.1.15.1 S3=<σ,τ>. Οι δυνατές τάξεις των υποομάδων της S3 είναι 1,2,3,6. Άρα οι μή τετριμμένες γνήσιες υποομάδες της S3 έχουν τάξη πρώτο αριθμό και επομένως είναι κυκλικές. Έτσι το διάγραμμα των υποομάδων της S3 με τον παραπάνω συμβολισμό είναι όπως στο Σχήμα 3.3

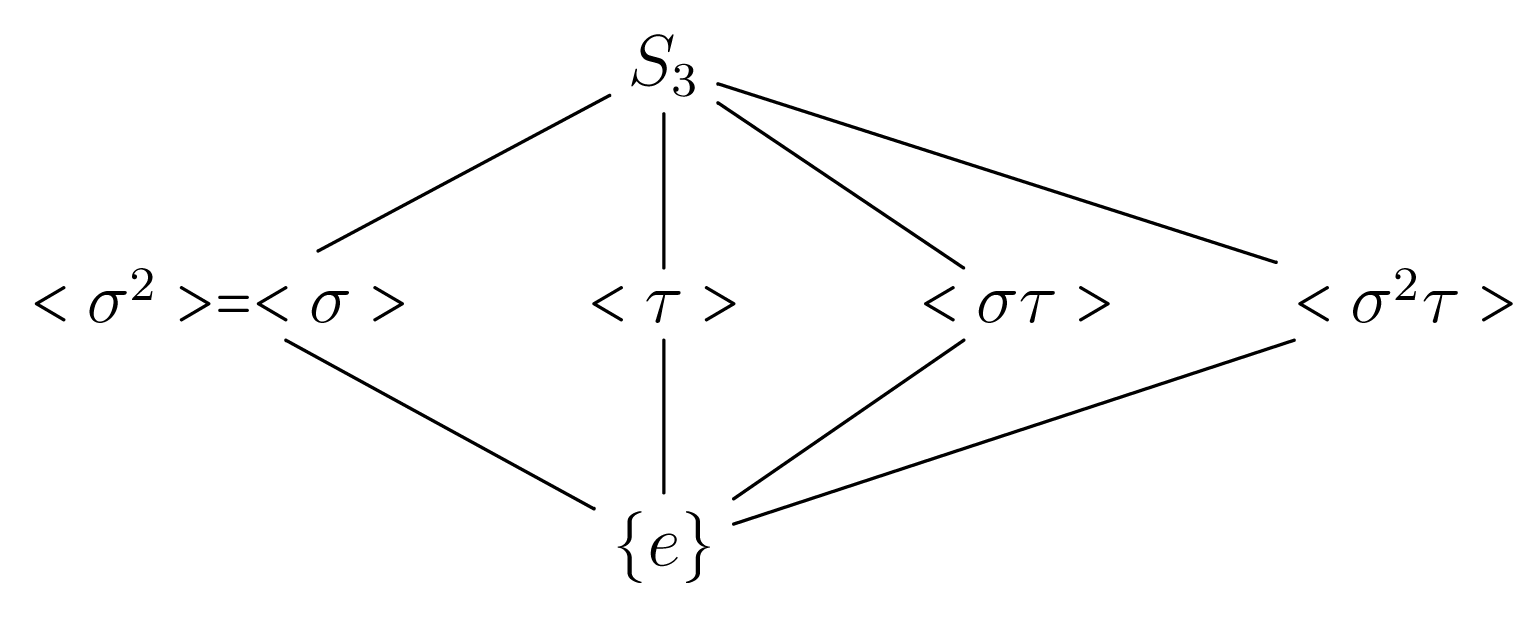Σχήμα 3.3

3. Το διάγραμμα των υποομάδων της διεδρικής ομάδας D2⋅4. Στο Παράδειγμα 1.1.2.4 ορίσαμε τη διεδρική ομάδα D2⋅4 και υπολογίσαμε τον πίνακα Cayley αυτής, ενώ στο Παράδειγμα 2.1.5.12 ορίσαμε τη διεδρική ομάδα D2.⁢n για n≥3. Από τη γεωμετρική ερμηνεία της D2.⁢n προκύπτει ότι η D2.⁢n παράγεται από τα στοιχεία ρ και ε και ακόμα ότι αυτά ικανοποιούν τις σχέσεις 2.1.1. Ιδιαίτερα είδαμε από τον ορισμό της D2.⁢n ότι

o⁢r⁢d⁢(ρ)=n,o⁢r⁢d⁢(ε)=2⁢ και ⁢o⁢r⁢d⁢(ρk⁢ε)=2, 0≤k≤n-1. 3.1.6

Η τελευταία από τις σχέσεις (3.1.6) είναι ισοδύναμη της τρίτης από τις σχέσεις (2.1.1), όπως έυκολα μπορούμε να διαπιστώσουμε. Αντίστροφα,τώρα, από τις σχέσεις (3.1.6) μπορούμε να υπολογίσουμε όλα τα στοιχεία της ομάδας D2.⁢n και να υπολογίσουμε τον πίνακα Cayley αυτής. Αφήνουμε αυτόν τον έλεγχο για τον αναγνώστη.

Έτσι αγνοώντας τη γεωμετρική ερμηνεία των στοιχείων ρ και ε ορίζουμε την αφηρημένη διεδρική ομάδα, η οποία λέγεται επίσης διεδρική ομάδα και συμβολίζεται πάλι ως D2.⁢n.

Ορισμός 3.1.15

Η (αφηρημένη) διεδρική ομάδα (abstract dyhedral) D2.⁢n είναι η ομάδα που παράγεται από τα στοιχεία α και β, τα οποία ικανοποιούν τις σχέσεις

o⁢r⁢d⁢(α)=n,o⁢r⁢d⁢(β)=2,o⁢r⁢d⁢(αk⁢β)=2, 0≤k≤n-1. (3.25)

Αν επιτρέψουμε το στοιχείο ρ, που αναφέρεται στον Ορισμό 3.1.14, να έχει άπειρη τάξη, τότε δημιουργούμε την ομάδα που παράγεται από τα στοιχεία ρ,ε τα οποία ικανοποιούν τις σχέσεις

o⁢r⁢d⁢(ρ)=∞,o⁢r⁢d⁢(ε)=2,o⁢r⁢d⁢(ρk⁢ε)=2,k∈ℕ. 3.1.7

Η ομάδα αυτή λέγεται γενικευμένη (generalized) διεδρική ομάδα και συμβολίζεται με D2.⁢∞.

Θα προχωρήσουμε, τώρα, στον υπολογισμό των υποομάδων της διεδρικής ομάδας D2⋅4. Θα χρησιμοποιήσουμε τους συμβολισμούς του Παραδείγματος 1.1.4.4 και ο πίνακας Cayley που αναφέρεται σε αυτό θα είναι χρήσιμος. Σύμφωνα με το θεώρημα του Lagrange μία γνήσια υποομάδα της D2⋅4 έχει τάξη 2 ή 4. Επομένως αυτές είναι οι κυκλικές υποομάδες τάξης 2 ή 4 καθώς οι ομάδες τάξης 4 που είναι ισόμορφες με την ομάδα του Klein. Από τον ορισμό της D2⋅4 τα μόνα στοιχεία τάξης 4 είναι το ρ, με <ρ≥{e,ρ,ρ2,ρ3} και το ρ3 αφού o⁢r⁢d⁢(ρ3)=4. Βέβαια <ρ≥<ρ3>. Επίσης τα στοιχεία ρ2,e,ρ⁢ε,ρ2⁢ε,ρ3⁢ε έχουν τάξη ίση με 2. Από τον ορισμό της ομάδας του Klein μία κυκλική υποομάδα της D2⋅4 τάξης 4 παράγεται από δύο στοιχεία τάξης 2. Δεν έχουμε, λοιπόν, παρά να πάρουμε ανά δύο τα πέντε στοιχεία τάξης 2 και να λάβουμε τις διακεκριμένες υποομάδες που θα προκύψουν. Έτσι θα λαμβάνουμε τις υποομάδες:

<ρ2,ε≥{e,ρ2,ε,ρ2ε}=<ρ2,ρ2ε≥<ε,ρ2ε>,<ρ2,ρε≥{e,ρ2,ρε,ρ3ε}=<ρ2,ρ3ε≥<ρε,ρ3ε>,<ε,ρε≥{e,ε,ρε,ρ3,ρ,ρ3ε,ρ2}=<ρ2ε,ρ3ε≥<ρε,ρ2ε≥<ε,ρ3ε≥D2⋅4. (3.26)

Για τον υπολογισμό των υποομάδων τάξης 2 δεν έχουμε παρά να βρούμε τα στοιχεία τάξης 2. Έτσι βρίσκουμε όλες τις γνήσιες υποομάδες της D2⋅4 και το διάγραμμα των υποομάδων της δίνεται στο Σχήμα 3.4.

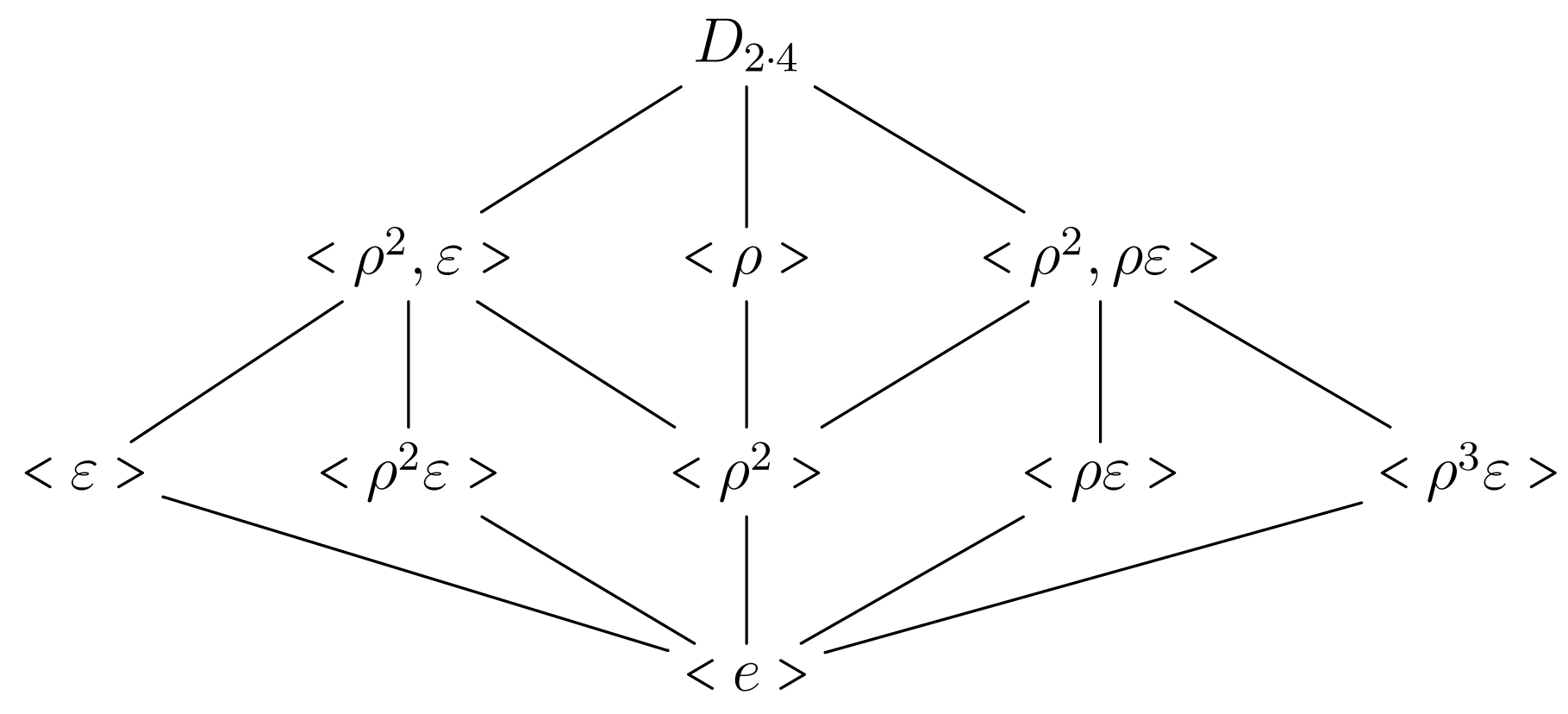Σχήμα 3.4

4. Το διάγραμμα των υποομάδων της τετραδικής ομάδας Q8. Τετραδική ομάδα, Q8, λέγεται η ομάδα με σύνολο το

Q8={1,-1,i,-i,j,-j,k,-k} (3.27)

και πίνακα Cayley τον Πίνακα 3.1


⋅ 		1 -1 i -i j -j k -k
1 1 -1 i -i j -j k -k
-1 -1 1 -i i -j j -k k
i i -i -1 1 k -k -j j
-i -i i 1 -1 -k k j -j
j j -j -k k -1 1 i -i
-j -j j k -k 1 -1 -i i
k k -k j -j -i i -1 1
-k -k k -j j i -i 1 -1

Πίνακας 3.1

Έτσι το 1 είναι το ουδέτερο στοιχείο της (Q8,⋅) και ακόμα τα στοιχεία της Q8 ικανοποιούν τις σχέσεις

(-1)⁢g=-g=g⁢(-1),g∈Q8,i2=j2=k2=-1i⁢j=kj⁢i=-kj⁢k=ik⁢j=-ik⁢i=ji⁢k=-j. (3.28)

Παρατηρούμε ότι o⁢r⁢d⁢(i)=o⁢r⁢d⁢(j)=4,o⁢r⁢d⁢(-1)=2. Ακόμη η Q8 παράγεται από τα στοιχεία i,j και οι σχέσεις που ικανοποιούν τα στοιχεία της Q8 μπορούν να περιοριστούν στις:

i4=1=j4,j⁢i=i3⁢j,i2=j2. 3.1.8

Ο αναγνώστης μπορεί να υπολογίσει του πίνακα Cayley της ομάδας που παράγεται από τα στοιχεία i,j και ικανοποιούν τις σχέσεις (3.1.8). Το αποτέλεσμα αυτής της προσπάθειας είναι ο πίνακας Cayley που εμφανίζεται παραπάνω και τον συμβολισμό j2=i2=-1. Ο υπολογισμός των υποομάδων της Q8 γίνεται με το σκεπτικό που αναπτύξαμε για την D2⋅4 και το αποτέλεσμα είναι το διάγραμμα υποομάδων της, όπως δίνεται στο Σχήμα 3.5

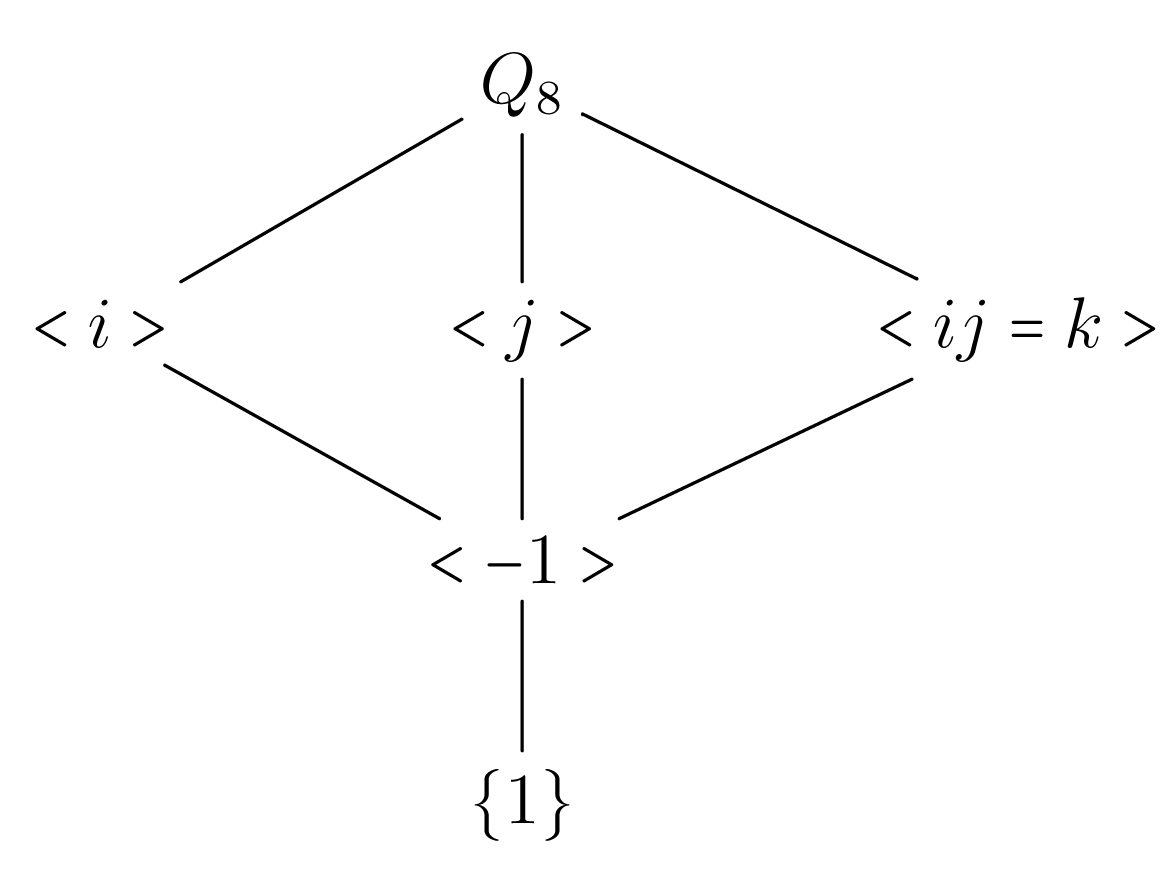Σχήμα 3.5

Θα κλείσουμε αυτό το εδάφιο με την επόμενη πρόταση που αναφέρεται σε ιδιότητες του δείκτη υποομάδας.

Πρόταση 3.1.16

Έστω G μία ομάδα και H,K≤G.

  1. i.

    Αν α,β∈G και H⁢α∩K⁢β≠Ø. τότε

    H⁢α∩K⁢β=(H∩K)⁢γ, (3.29)

    για κάποιο γ∈G. Η πρόταση ισχύει και για αριστερές κλάσεις.

  2. ii.

    [G:H∩K]≤[G:H][G:K].

  3. ii.

    Αν ([G:H],[G:K])=1, τότε [G:H∩K]=[G:H][G:K].

Απόδειξη:

  1. i.

    Έστω ότι H⁢α∩K⁢β≠Ø, για α,β∈G και γ∈H⁢α∩K⁢β. Τότε γ∈H⁢α και γ∈K⁢β. Άρα H⁢γ=H⁢α και K⁢γ=K⁢β, εφόσον οι H⁢α και K⁢β είναι κλάσεις σχέσεων ισοδυναμίας. Επομένως,

    H⁢α∩K⁢β=H⁢γ∩K⁢γ. (3.30)

    Όμως, εύκολα διαπιστώνεται ότι

    H⁢γ∩K⁢γ=(H∩K)⁢γ, (3.31)

    άρα

    H⁢α∩K⁢β=(H∩K)⁢γ, (3.32)

    για κάποιο γ∈G. Όμοια αποδεικνύεται το συμπέρασμα αυτό για αριστερές κλάσεις και αποδείχθηκε το i).

  2. ii.

    Έστω ότι [G:H]=m και [G:K]=n. Αν m=∞⁢ ή ⁢n=∞, τότε το συμπέρασμα είναι φανερό. Υποθέτουμε, λοιπόν, ότι m,n∈ℕ. Επομένως υπάρχουν m πλήθους δεξιές κλάσεις της Η στη G και n πλήθους δεξιές κλάσεις στης Κ στη G. Αυτό σημαίνει ότι υπάρχουν το πολύ m⋅n μη κενά σύνολα H⁢α∩K⁢β. Ομως, σύμφωνα με το i) κάθε μη κενό σύνολο H⁢α∩K⁢β είναι μία δεξιά κλάση της H∩K στην ομάδα G. Άρα

    [G:H∩K]≤[G:H][G:K] (3.33)

    και αποδείχθηκε το ii).

  3. iii.

    Με τους συμβολισμούς της απόδειξης του ii. για τα m και n υποθέτουμε ότι (m,n)=1. Από την άσκηση 13 προκύπτουν οι σχέσεις

    [G:H∩K]=[G:H][H:H∩K] 3.1.9

    και

    [G:H∩K]=[G:K][K:H∩K]. 3.1.10

    Έστω K=[G:H∩K]. Από τις σχέσεις 3.1.9, 3.1.10 και το γεγονός ότι (m,n)=1, έπεται ότι nm|k. Όμως, από το ii) ισχύει ότι k≤m⋅n, επομένως για τους φυσικούς αριθμούς m,n,k, ισχύει ότι m⁢n=k, που αποδεικνύει το iii). ■

Ασκήσεις

1. Να αποδείξετε την Πρόταση 3.1.1.
2. Έστω G μία ομάδα και H≤G. Να αποδείξεται ότι H2=H.
3. Έστω G μία ομάδα και Α ένα πεπερασμένο υποσύνολο της G τέτοιο, ώστε A2=A. Να αποδείξετε ότι A≤G. Η πρόταση αυτή ισχύει αν το Α δεν είναι πεπερασμένο;
4. Έστω G μία ομάδα και H≤G.

  1. i.

    Να αποδείξετε ότι, για α∈G,α⁢H≤G⇔α∈H.

  2. ii.

    Να αποδείξετε ότι, για α⁢β∈G,α⁢H=β⁢H⇔β-1⁢α∈H.

5. Έστω G μία ομάδα,H,K≤G και α,β∈G. Να αποδείξετε ότι αν α⁢H=β⁢K, τότε H=K.
6. Έστω G μία ομάδα, H≤G και α∈G. Να αποδείξετε ότι οι αντιστοιχίες

ϕ:H⟶α⁢H,h↦α⁢hf:H⟶H⁢α,h↦h⁢α

είναι αμφιμονότιμες και επί συναρτήσεις, δηλ. τα σύνολα H,α⁢H και H⁢α έχουν την ίδια ισχύ.
7. Να αποδείξετε ότι:

  1. 1.

    [ℤ:<n>]=n,n∈ℤ∖{0}.

  2. 2.

    [Sn:An]=2.

  3. 3.

    [ℚ:ℤ]=∞.

8. Έστω G μία ομάδα και Ø⊂A⊆G. Να αποδείξετε ότι η σχέση

α∼β⇔α⁢β-1∈A,α,β∈A, (3.34)

είναι σχέση ισοδυναμίας στο G αν και μόνον αν A≤G.
Είναι η σχέση

α∼′β⇔A⁢α=A⁢β,α,β∈A, (3.35)

σχέση ισοδυναμίας στο G;
9. Να αποδείξετε ότι μία ομάδα G είναι πεπερασμένη αν και μόνον αν έχει πεπερασμένου πλήθους υποομάδες.
10. Να αποδείξετε ότι ικανή και αναγκαία συνθήκη ώστε μία αβελιανή ομάδα να μην έχει γνήσιες υποομάδες είναι να έχει τάξη πρώτο αριθμό.
11. Έστω G μία ομάδα και H,K∈G τετοιες, ώστε (|H|,|K|)=1. Να αποδείξετε ότι H∩K={e}.
12. Έστω G μία ομάδα και H,K≤G. Να αποδείξετε ότι

|H⁢K|=|H|⁢|K||H∩K|. (3.36)

13. Έστω G μία ομάδα και H,K≤G τέτοιες, ώστε H≤K≤G. Να αποδείξετε ότι

[G:H]=[G:K][K:H]. (3.37)

3.2 Κανονικές υποομάδες

Ένα εύλογο ερώτημα που δημιουργείται από τις σχέσεις (3.1.3) και (3.1.4) είναι αν ισχύει H⁢α=α⁢H, για κάθε α∈G, όπου Η είναι μία υποομάδα της ομάδας G. Βέβαια η απάντηση είναι καταφατική αν η G είναι αβελιανή ομάδα. Ενώ από τον πίνακα Cayley της S3, βλ. Παράδειγμα 2.1.15.1, παρατηρούμε ότι

g<σ≥<σ>⁢g, για κάθε ⁢g∈S3 (3.38)

και

σ<τ≥{σ,σ⁢τ}≠<τ>⁢σ={σ,σ2⁢τ}. (3.39)

Συμπεραίνουμε ότι κάποιες υποομάδες μίας ομάδας έχουν την παραπάνω ιδιότητα και κάποιες όχι. Έτσι δικαιολογείται ο επόμενος ορισμός.

Ορισμός 3.2.1

Έστω G μία ομάδα και H≤G. Η υποομάδα Η λέγεται κανονική ή αναλλοίωτη (normal) αν

g⁢H=H⁢g, για κάθε ⁢g∈G, (3.40)

ή ισοδύναμα, αν

H=g⁢H⁢g-1, για κάθε ⁢g∈G, (3.41)

και συμβολίζεται H⊴G ή H⊲G όταν είναι σαφές ότι H⫋G.

Παρατηρήσεις 3.2.2

i. Η σχέση g⁢H=H⁢g στον Ορισμό 3.2.1 σημαίνει ότι τα δύο σύνολα είναι ίσα και όχι ότι το στοιχείο g αντιμετατίθεται με κάθε στοιχείο της Η. Έτσι αν h∈H, τότε το g⁢h∈H⁢g. Άρα υπάρχει h′∈H ώστε g⁢h=h′⁢g, φυσικά από τη σχέση αυτή δεν μπορούμε να συμπεράνουμε ότι h=h′.

ii. Από τον Ορισμό 3.2.1 προκύπτει αμέσως ότι H⊴G αν και μόνον αν η Η ταυτίζεται με όλες τις συζυγείς υποομάδες της.

Πριν προχωρήσουμε σε παραδείγματα, ας δούμε ένα κριτήριο των κανονικών υποομάδων που θα είναι χρήσιμο για να ελαχιστοποιούμε τις απαιτούμενες πράξεις ώστε να ελέγχουμε αν μία υποομάδα είναι κανονική.

Θεώρημα (Κριτήριο) 3.2.3

Έστω G μία ομάδα και H≤G. Τότε

H⊴G⇔g⁢H⁢g-1⊆H, για κάθε ⁢g∈G. (3.42)

Απόδειξη: Έστω G μία ομάδα και H≤G. Αν H⊴G, το συμπέρασμα είναι φανερό. Έστω αντίστροφα ότι

g⁢H⁢g-1⊆H, για κάθε ⁢g∈G. 3.2.1

Η σχέση (3.2.1) ισχύει για κάθε g, άρα και για το g-1. Άρα

g-1⁢H⁢g⊆H⇒H⊆g⁢H⁢g-1, για κάθε ⁢g∈G. (3.43)

Αυτή η τελευταία σχέση μάζι με την (3.2.1) μας οδηγεί στο συμπέρασμα ότι

g⁢H⁢g-1=H, για κάθε ⁢g∈G, (3.44)

που αποδεικνύει το Θεώρημα. ■

Παραδείγματα 3.2.4

1. Οι {e} και G είναι κανονικές υποομάδες μίας ομάδας G.

2. S⁢Ln⁢(ℝ)⊴G⁢Ln⁢(ℝ). Πράγματι έστω A∈S⁢Ln⁢(ℝ) και B∈G⁢Ln⁢(ℝ), τότε, από τις ιδιότητες των οριζουσών, έχουμε

d⁢e⁢t⁢(B⁢A⁢B-1)=d⁢e⁢t⁢(B)⁢d⁢e⁢t⁢(A)⁢d⁢e⁢t⁢(B-1)=d⁢e⁢t⁢(B)⁢d⁢e⁢t⁢(B-1)=1. (3.45)

Άρα

B⁢S⁢Ln⁢(ℝ)⁢B-1⊆S⁢Ln⁢(ℝ), για κάθε ⁢B∈G⁢Ln⁢(ℝ), (3.46)

και σύμφωνα με το κριτήριο της κανονικής υποομάδας (Θεώρημα 3.2.3) ) S⁢Ln⁢(ℝ)⊴G⁢Ln⁢(ℝ).

Πρόταση 3.2.5

Έστω G μία ομάδα και H≤G. Αν [G:H]=2, τότε H⊴G.

Απόδειξη Από τη σχέση [G:H]=2, έπεται ότι

G=H⁢⊍⁢α⁢H=H⁢⊍⁢H⁢β, 3.2.2

για κάποια στοιχεία α,β∈G. Προφανώς τα α,β δεν ανήκουν την Η, δηλ α,β∈G\H. Τότε β∈α⁢H και α⁢H=β⁢H. Άρα η σχέση 3.2.2 γίνεται

G=H⁢⊍⁢β⁢H=H⁢⊍⁢H⁢β (3.47)

και, επειδή β⁢H=G\H και H⁢β=G\H, έπεται ότι

β⁢H=H⁢β. 3.2.3

Μένει να δείξουμε ότι g⁢H=H⁢g, για κάθε g∈G. Βέβαια η σχέση αυτή ισχύει αν g∈H, αφού τότε g⁢H=H=H⁢g. Έστω g∉H, τότε

g∈βH⇒g=βh, για κάποιο h∈H,⇒H⁢g=H⁢β⁢h=β⁢H⁢h=β⁢H⁢ και ⁢g⁢H=β⁢h⁢H=β⁢H.

Επομένως, απο τη σχέση (3.2.3), έπεται ότι

H⁢g=g⁢H, για κάθε ⁢g∈H, (3.48)

δηλ. H⊴G. ■

Παρατήρηση 3.2.6

Το αντίστροφο της Πρότασης 3.2.5 δεν ισχύει. Υπάρχουν υποομάδες H≤G με [G:H]≠2, αλλά H⊴G. Τέτοιο παράδειγμα είναι η ℤn με n ένα σύνθετο φυσικό. Τότε υπάρχει υποομάδα Η της ℤn με τάξη k|n,k≠1 με [ℤn:H]=n/k (βλ. Θεώρημα 3.1.12). Η H⊴ℤn γιατί η ℤn είναι αβελιανή.

Παραδείγματα 3.2.7

1. Η υποομάδα <σ> της S3 (βλ. Παράδειγμα 3.1.8.2) είναι κανονική, γιατί [S3:<σ>]=2. Ο αναγνώστης εκτελώντας τις σχετικές πράξεις μπορεί να αποδείξει ότι η <σ> είναι η μόνη γνήσια κανονική υποομάδα της S3.

2. Κανονικές υποομάδες της D2⋅4. Από το διάγραμμα υποομάδων της D2⋅4 (βλ. Παράδειγμα 3.1.13.3) οι υποομάδες <ρ2,ε>,<ρ>,<ρ2,ρε> είναι κανονικές γιατί έχουν δείκτη στην ομάδα D2⋅4 ίσο με 2. Παρατηρούμε ότι <ρ2>⊴<ρ>, γιατί η <ρ> είναι αβελιανή κυκλική και έτσι

<ρ2>⊴<ρ>⊴D2⋅4. (3.49)

Η <ρ2> είναι κανονική υποομάδα της D2⋅4; Από τις σχέσεις πολλαπλασιασμού των στοιχείων της D2⋅4 (βλ σχέση (3.1.6) ) έχουμε, για 1≤k≤3,

ρk⁢ε⁢ρ2⁢(ρk⁢ε)-1=ρk⁢ε⁢ρ2⁢ε⁢ρ-k=ρk⁢ρ2⁢ε⁢ε⁢ρ-k=ρ2. (3.50)

Άρα

g⁢<ρ2>⁢g-1⊆<ρ2>, για κάθε ⁢g∈D2⋅4, (3.51)

δηλ <ρ2>⊴D2⋅4. Θεωρούμε τώρα την <ρ2,ε>, τότε <ε>⊴<ρ2,ε>⊴D2⋅4. Όμως η <ε> δεν είναι κανονική υποομάδα της D2⋅4. Πράγματι βλέπουμε ότι ρ⁢<ε>⁢ρ-1={e,ρ⁢ε⁢ρ-1}={e,ρ2⁢ε}≠{e,ε}. Ο αναγνώστης καλείται να υπολογίσει όλες τις κανονικές υποομάδες της D2⋅4.
Aπό τα παραπάνω έχουμε το ακόλουθο.

Συμπέρασμα 3.2.8

Έστω G μία ομάδα και H,K≤G. Από τη σχέση H⊴K⊴G⇏H⊴G.

3. Κανονικές υποομάδες της Q8. Από το διάγραμμα των υποομάδων της Q8 (βλ. Παράδειγμα 3.1.13.4) παρατηρούμε ότι οι υποομάδες <i>, <j>,<k> είναι κανονικές, αφού έχουν δείκτη 2 στην Q8. Η υποομάδα <-1> είναι επίσης κανονική γιατί, για κάθε g∈Q8, ισχύει g⁢<-1>⁢g-1={1,-1}=<-1>. Συμπεραίνουμε, λοιπόν, ότι όλες οι υποομάδες της Q8 είναι κανονικές. Όπως γνωρίζουμε, αν G είναι μία αβελιανή ομάδα, τότε κάθε υποομάδα της είναι κανονική. Το αντίστροφο, όμως, αυτής της πρότασης δεν ισχύει και η Q8 είναι ένα αντιπαράδειγμα.

4. Θεωρούμε την ομάδα D2⋅4, (βλ. Παράδειγμα 3.1.13.4). Η υποομάδα της <p>⊴D2⋅4, διότι [D2⋅4:H]=2.

Συνεχίζουμε με μερικές ιδιότητες των κανονικών ομάδων.

Θεώρημα 3.2.9

Έστω {Hi,i∈I} μία οικογένεια κανονικών υποομάδων μίας ομάδας G. Τότε

∩i∈IHi⊴G. (3.52)

Απόδειξη: Έστω H=∩i∈IHi. Από την Πρόταση 2.1.7 προκύπτει ότι H≤G. Από το Θεώρημα 3.2.3 έπεται ότι προκειμένου να αποδείξουμε ότι H⊴G, αρκεί να αποδείξουμε ότι g⁢h⁢g-1∈H, για κάθε g∈G και για κάθε h∈H. Έστω, λοιπόν, g∈G και h∈H. Τότε h∈Hi⊴G και g⁢h⁢g-1∈Hi για κάθε i∈I. Άρα g⁢h⁢g-1∈∩i∈IHi=H, δηλ H⊴G. ■

Πρόταση 3.2.10

Έστω G μία ομάδα και Η,Κ δύο κανονικές υποομάδες της G, τότε H⁢K⊴G.

Απόδειξη Εφόσον οι Η,Κ είναι κανονικές υποομάδες της G, παρατηρούμε ότι

H⁢K=∪k∈KH⁢k=∪k∈Kk⁢H=K⁢H. (3.53)

Άρα H⁢K≤G, (βλ. Πρόταση 3.1.2). Έστω τώρα g∈G, τότε

g⁢H⁢K⁢g-1=g⁢H⁢g-1⁢g⁢K⁢G-1=H⁢K, για κάθε ⁢g∈G. (3.54)

Επομένως H⁢K⊴G. ■

Πρόταση 3.2.11

Έστω G μία ομάδα και H,K,L≤G τέτοιες ώστε H⊴K. Τότε L∩H⊴L∩K.

Απόδειξη Από την Πρόταση 2.1.7 έπεται ότι L∩H,L∩K≤G. Αφού H≤K είναι φανερό ότι ισχύει L∩H≤L∩K. Ας θεωρήσουμε, τώρα, ένα τυχαίο στοιχείο x∈L∩K και ένα τυχαίο y∈L∩H. Αρκεί να αποδείξουμε ότι x⁢y⁢x-1∈L∩H. Είναι φανερό ότι x⁢y⁢x-1∈L. Ακόμη, αφού H⊴K,x∈K και y∈H, έπεται ότι x⁢y⁢x-1∈H. Άρα x⁢y⁢x-1∈L∩H, έτσι αποδείξαμε ότι L∩H⊴L∩K. ■

Μία ενδιαφέρουσα υποομάδα της G είναι το κέντρο της.

Ορισμός 3.2.12

Κέντρο (center) μίας ομάδας G λέγεται το σύνολο

Z⁢(G):={x∈G:g⁢x=x⁢g,∀g∈G}. (3.55)

Πολλές φορές το κέντρο Z⁢(G) μίας ομάδας συμβολίζεται και ως C⁢(G). Παρατηρούμε ότι Z⁢(G)=G αν και μόνον αν η ομάδα G είναι αβελιανή. Έτσι θα μπορούμε να πούμε ότι το Z⁢(G) ((μετράει)) πόσο ((απέχει)) η G από το να είναι αβελιανή.

Πρόταση 3.2.13

Έστω G μία ομάδα, τότε Z⁢(G)⊴G.

Απόδειξη Θα αποδείξουμε πρώτα ότι Z⁢(G)≤G. Έστω x∈Z⁢(G), τότε, για κάθε g∈G, ισχύει

g⁢x=x⁢g⇔x-1⁢g=g⁢x-1⇒x-1∈Z⁢(G). (3.56)

Τώρα, αν x,y∈Z⁢(G) και g∈G, έχουμε g⁢(x⁢y-1)=x⁢g⁢y-1=(x⁢y-1)⁢g. Άρα x⁢y-1∈Z⁢(G) και συνεπώς Z⁢(G)≤G. Τέλος

g⁢x⁢g-1=x⁢g⁢g-1=x, για όλα τα ⁢x∈Z⁢(G), και ⁢g∈G, (3.57)

δηλ. g⁢Z⁢(G)⁢g-1⊂Z⁢(G) και συνεπώς Z⁢(G)⊴G. ■

Παραδείγματα 3.2.14

1. Θα αποδείξουμε ότι Z⁢(G⁢L2⁢(ℝ))={(α00α):α∈ℝ*}. Έστω

A:=(αβγδ)∈Z⁢(G⁢L2⁢(ℝ)). (3.58)

Τότε το Α αντιμετατίθεται με κάθε στοιχείο της G⁢L2⁢(ℝ), επομένως και με τα στοιχεία (-1001),(1010). Έτσι

A⁢(-1001)=(-1001)⁢A⇔β=γ=0 (3.59)

και

A⁢(0110)=(0110)⁢A⇔α=δ. (3.60)

Άρα

A=(α00α)∈Z⁢(G⁢L2⁢(ℝ)) (3.61)

για α∈ℝ*. Ισχύει, όμως, και το αντίστροφο και αποδείχθηκε η πρόταση.

2. Το κέντρο της D2⋅4 είναι η <ρ2>. Αρκεί να παρατηρήσουμε ότι ρ2⁢ε=ε⁢ρ2 και να εφαρμόσουμε τις σχέσεις (2.1.1).

3. Το κέντρο της Q8 είναι η ομάδα <-1>, όπως διαπιστώνεται από τον πίνακα Cayley της Q8 ή τις σχέσεις 3.1.8.

4. Το κέντρο της S3 είναι η {e}.

Η επόμενη πρόταση εξετάζει τον πυρήνα ενός ομομορφισμού ομάδων ως προς την κανονικότητά του.

Πρόταση 3.2.15

Έστω ϕ:G→H ένας ομομορφισμός ομάδων. Τότε K⁢e⁢r⁢ϕ⊴G.

Απόδειξη Γνωρίζουμε ότι K⁢e⁢r⁢ϕ≤G (βλ. Πρόταση 2.3.7) αρκεί επομένως να δείξουμε ότι

g⁢α⁢g-1∈K⁢e⁢r⁢ϕ, για κάθε ⁢g∈G⁢ και ⁢α∈K⁢e⁢r⁢ϕ 3.2.4

Όμως

ϕ⁢(g⁢α⁢g-1)=ϕ⁢(g)⁢ϕ⁢(α)⁢ϕ⁢(g-1)=ϕ⁢(g)⁢e⁢ϕ⁢(g)-1=e. (3.62)

Άρα αποδείχθηκε η σχέση (3.2.4). ■

Το επόμενο είναι ενδεικτικό της σπουδαιότητας της κανονικής υποομάδας για τη μελέτη της δομής της ομάδας.

Θεώρημα 3.2.16

Έστω G μία ομάδα και H≤G. Το σύνολο των αριστερών ή των δεξιών κλάσεων της Η στη G αποτελεί υποομάδα με πράξη τον πολλαπλασιασμό υποσυνόλων της G αν και μόνον αν η Η είναι κανονική υποομάδα της G.

Απόδειξη Ας υποθέσουμε ότι H⊴G, τότε, για τυχαία α,β∈G, ισχύει

α⁢H⁢β⁢H=α⁢β⁢H⁢H=α⁢β⁢H. (3.63)

Αυτό σημαίνει ότι το γινόμενο δύο στοιχείων του συνόλου G/H={g⁢H:g∈G} ανήκει σε αυτό. Το γινόμενο υποσυνόλων μίας ομάδας έχει την προσεταιριστική ιδιότητα, βλ. Πρόταση 3.1.1, i). Παρατηρούμε ότι g⁢H⁢H=H, για κάθε g∈G, άρα το Η είναι δεξιό ουδέτερο στοιχείο του G/H. Τέλος βλέπουμε ότι, για κάθε g∈G, και αφού H⊴G, ισχύει

g⁢H⁢g-1⁢H=g⁢g-1⁢H⁢H=H, (3.64)

δηλ το στοιχείο g-1⁢H∈G/H είναι δεξιό αντίστροφο του g⁢H. Επομένως το G/H αποτελεί ομάδα σύμφωνα με το Θεώρημα 1.2.2.
Αντίστροφα τώρα, ας υποθέσουμε ότι το σύνολο G/H={g⁢H:g∈G} αποτελεί υποομάδα με πράξη τον πολλαπλασιαμό υποσυνόλων της G. Τότε το Η είναι το ουδέτερο στοιχείο της G/H και για κάθε στοιχείο g∈G ισχύει

H⁢g⁢H=g⁢H⇒H⁢g⊂g⁢H⇒g-1⁢H⁢g⊆H, (3.65)

δηλ. H⊴G.
Ανάλογα εργαζόμαστε για τις δεξιές κλάσεις Η στην G/H. ■

Ορισμός 3.2.17

Έστω G μία ομάδα και H⊴G. Η ομάδα

G/H={g⁢H:g∈G} (3.66)

λέγεται ομάδα πηλίκο (factor group) της Η στην ομάδα G.

Είναι φανερό από το Θεώρημα του Lagrange ότι αν η ομάδα G είναι πεπερασμένη και H⊴G, τότε |G/H|=|G||H|.

Ακόμη παρατηρούμε ότι κάθε ομάδα πηλίκο μίας αβελιανής ομάδας είναι αβελιανή.

Πρόταση 3.2.18

Έστω G μία ομάδα και H⊴G. Τότε υπάρχει ένας ομομορφισμός

ϕ:G⟶G/H,g⟼g⁢H, (3.67)

με πυρήνα την ομάδα Η. Η ϕ λέγεται φυσικός (natural) ομομορφισμός της G.

Η απόδειξη αφήνεται για τον αναγνώστη. ■

Ας δούμε μία ενδιαφέρουσα εφαρμογή του Θεωρήματος 3.2.17.

Θεώρημα 3.2.19

Ικανή και αναγκαία συνθήκη για να είναι μία ομάδα αβελιανή είναι η ομάδα G/Z⁢(G) να είναι κυκλική.

Απόδειξη Έστω G μία αβελιανή ομάδα, τότε Z⁢(G)=G και η ομάδα G/G είναι τετριμμένη, άρα κυκλική. Για το αντίστροφο, έστω G μία ομάδα τέτοια, ώστε η ομάδα G/Z⁢(G) να είναι κυκλική. Αυτό σημαίνει ότι υπάρχει ένα στοιχείο g⁢Z⁢(G)∈G/Z⁢(G), ώστε

G/Z(G)=<gZ(G)≥{(gZ(G))n:n∈ℤ}={gnZ(G):n∈ℤ}, (3.68)

γιατί g⁢Z⁢(G)⁢g⁢Z⁢(G)=g2⁢Z⁢(G)2=g2⁢Z⁢(G) και επαγωγικά ισχύει ότι (g⁢Z⁢(G))n=gn⁢Z⁢(G). Κάθε στοιχείο της ομάδας G ανήκει σε μία μόνο κλάση gn⁢Z⁢(G), για κάποιο n∈ℤ (βλ. σχέση 3.1.4). Επομένως, αν α,β∈G, τότε α=gk⁢ζ1 και β=gλ⁢ζ2, για κάποιους ακέραιους κ,λ και για κάποια στοιχεία ζ1,ζ2∈Z⁢(G). Έτσι

α⁢β=gk⁢ζ1⁢gλ⁢ζ2=gk⁢gλ⁢ζ1⁢ζ2=gλ⁢gk⁢ζ2⁢ζ1=gλ⁢ζ2⁢gk⁢ζ1=β⁢α, (3.69)

άρα η ομάδα G είναι αβελιανή. ■

Ασκήσεις

1. Έστω G μία ομάδα και Hi⊴G, 1≤i≤n. Να αποδείξετε ότι H1⁢H2⁢…⁢Hn⊴G.
2. Δίνεται μία G και H⊴G. Αν για τα στοιχεία x,y∈G, ισχύει x⁢y∈H, να αποδείξετε ότι y⁢x∈H. Ισχύει η πρόταση αυτή αν η Η δεν είναι κανονική υποομάδα της G;
3. Έστω G μία ομάδα και H,K∈G τέτοιες, ώστε K⊴G. Να αποδείξετε ότι H∩K⊴H και H⁢K<G.
4. Δίνεται μία ομάδα G, H⊴G και K⊴G τέτοιες ώστε H∩K={e}. Να αποδείξετε ότι h⁢k=k⁢h, για όλα τα στοχεία h∈H και k∈K.
5. Αν G είναι μία ομάδα, H⊴G και H<K<G, να αποδείξετε ότι H⊲K.
6. Έστω G μία ομάδα και H≤G με την ιδιότητα: Κάθε αριστερή κλάση της Η στην ομάδα G να είναι και δεξιά κλάση της Η στην ομάδα G. Να εξετάσετε αν H⊴G.
7. Έστω α,β,γ στοιχεία μίας ομάδας G έτσι ώστε α⁢β=γ και γ∈Z⁢(G). Να αποδείξετε ότι α⁢β=β⁢α.
8. Έστω G μία ομάδα και K⊴G τέτοια, ώστε |K|=2. Να αποδείξετε ότι K≤Z⁢(G).
9. Έστω G μία ομάδα και H≤Z⁢(G). Να αποδείξετε ότι H⊴Z⁢(G).
10. Δίνεται μία ομάδα G και m ένας φυσικός αριθμός που διαιρεί την |G|. Αν υπάρχει μοναδική υποομάδα Η της G με τάξη m, να αποδείξετε ότι H⊴G.
11. Δίνεται ομάδα G και H,K≤G τέτοιες ώστε K≤H≤G και K⊴G. Να αποδείξετε ότι K⊴⋂α∈Gα⁢H⁢α-1.
12. Έστω α ένα στοιχείο μίας ομάδας G τέτοιο ώστε g-1⁢α⁢g⁢α∈Z⁢(G), για κάθε g∈G. Να αποδείξετε ότι η αντιστοιχία

f:G⟶Z⁢(G),g⟼g-1⁢α-1⁢g⁢α (3.70)

είναι ομομορφισμός ομάδων.
13. Να αποδείξετε ότι Z⁢(G⁢Ln⁢(ℝ))={α⁢In:α∈ℝ*}.
14. Να αποδείξετε ότι η αντιστοιχία

f:G⁢Ln⁢(ℝ)/S⁢Ln⁢(ℝ)⟶ℝ*,A⋅S⁢Ln⁢(ℝ)⟼d⁢e⁢t⁢A (3.71)

είναι ισομορφισμός ομάδων.
15. Έστω H={(αβ0γ):(αx0β)∈G⁢L2⁢(ℝ)}. Να αποδείξετε ότι

H<G⁢L2⁢(ℝ)⁢ και ⁢Z⁢(H)=Z⁢(G⁢L2⁢(ℝ)). (3.72)

16. Να αποδείξετε ότι η ομάδα Q8/Z⁢(Q8) είναι ισόμορφη με την (ℤ4,+).
17. Έστω G μία ομάδα. Μία υποομάδα Η της G λέγεται χαρακτηριστική (characteristic) αν f⁢(H)⊆H για κάθε f∈A⁢u⁢t⁢G. Να αποδείξετε ότι η Z⁢(G) είναι μία χαρακτηριστική υποομάδα της G.
18. Δίνεται μία ομάδα G και N⊴G. Αν α∈G και o⁢r⁢d⁢(α)<∞, να αποδείξετε ότι o⁢r⁢d⁢(α⁢N)<∞. Να χρησιμοποιήσετε τη (ℤ,+) για να αποδείξετε ότι δεν ισχύει το αντίστροφο.
19. Δίνεται μία ομάδα G και N⊴G τέτοια ώστε [G:N]=n<∞. Να αποδείξετε ότι αn∈N, για κάθε α∈G.
20. Δίνεται ένας ομομορφισμός ομάδων f:G→H και N⊴G. Αν ϕ:G→G/N είναι ο φυσικός ομομορφισμός, να αποδείξετε ότι υπάρχει ομομορφισμός t τέτοιος ώστε το ακόλουθο διάγραμμα

(3.73)

να είναι αντιμεταθετικό (commutative diagram), δηλ. t∘ϕ=f.
21. Έστω G μία ομάδα και H<Z⁢(G). Να αποδείξετε ότι αν η ομάδα G/H είναι κυκλική, τότε η ομάδα G είναι αβελιανή (βλ. άσκ. 9).

3.3 Θεωρήματα Ισομορφίας

Τα θεωρήματα ισομορφίας έχουν ιδιαίτερη αξία στη Θεωρία Ομάδων και στην Άλγεβρα γενικότερα, αφού προσφέρουν τρόπους να συγκρίνονται αλγεβρικές δομές μεταξύ τους. Τα θεωρήματα ισομορφίας έχουν ανάλογες διατυπώσεις για όλες τις αλγεβρικές δομές π.χ. διανυσματικούς χώρους, ομάδες, δακτυλίους, modules κ.λ.π. Φυσικά εδώ θα ασχοληθούμε με τα θεωρήματα ισομορφίας ομάδων.

Η επόμενη πρόταση συγκεντρώνει τις βασικές ιδιότητες των ομάδων που δημιουργούνται από έναν ομομορφισμό ομάδων.

Πρόταση 3.3.1

Έστω f:G→H ένας επιμορφισμός ομάδων.

  1. i.

    Αν K≤H, τότε f-1⁢(K):={g∈G:f⁢(g)∈K}≤G.

  2. ii.

    Αν N⊴G, τότε f⁢(N)⊴H.

  3. iii.

    Αν K⊴H, τότε f-1⁢(K)⊴G.

  4. iv.

    Αν N≤G, τέτοια ώστε K⁢e⁢r⁢f≤N, τότε f-1⁢f⁢(N)=N.

  5. v.

    Έστω A:={X:K⁢e⁢r⁢f≤X≤G} και B:={Y:Y≤H}. Η αντιστοιχία

    F:A⟶B,X⟼f⁢(X) (3.74)

    είναι αμφιμονότιμη και επί συνάρτηση. Η συνάρτηση αυτή αντιστοιχεί κανονικές υποομάδες της G σε κανονικές υποομάδες της Η.

Απόδειξη

  1. i.

    Εφαρμόζουμε το κριτήριο της υποομάδας. Έστω x,y∈f-1⁢(K), τότε f⁢(x)=α και f⁢(y)=β, για κάποια στοιχεία α,β∈K. Έτσι,

    f⁢(x⁢y-1)=f⁢(x)⁢f⁢(y-1)=f⁢(x)⁢f⁢(y)-1=α⁢β-1∈K, (3.75)

    άρα x⁢y-1∈f-1⁢(K) και f-1⁢(K)≤G.

  2. ii.

    Έστω N⊴G. Γνωρίζουμε ότι f⁢(N)≤H (βλ. Πρόταση 2.3.3, iii). Θα αποδείξουμε ότι f⁢(N)⊴H, ισοδύναμα ότι, για κάθε h∈H και για κάθε x∈f⁢(N),h⁢x⁢h-1∈f⁢(N). Έστω, λοιπόν, h τυχόν στοιχείο της Η και x τυχόν στοιχείο του f⁢(N). Εφόσον η f είναι επιμορφισμός έπεται ότι υπάρχει α∈G, ώστε f⁢(α)=h. Επίσης, από τον ορισμό του f⁢(N) υπάρχει β∈N, ώστε x=f⁢(β). Άρα από την υπόθεση ότι N⊴G, έχουμε

    h⁢x⁢h-1=f⁢(α)⁢f⁢(β)⁢f⁢(α)-1=f⁢(α)⁢f⁢(β)⁢f⁢(α-1)=f⁢(α⁢β⁢α-1)∈f⁢(N) (3.76)

    και αποδείχθηκε το ii).

  3. iii.

    Έστω g∈G και α∈f-1⁢(K), τότε f⁢(α)∈K. Επομένως, για κάθε g∈G και κάθε α∈f-1⁢(K), έχουμε

    f⁢(g⁢α⁢g-1)=f⁢(g)⁢f⁢(α)⁢f⁢(g)-1∈K, (3.77)

    αφού K⊴H. Άρα g⁢α⁢g-1∈f-1⁢(K), για κάθε g∈G και α∈f-1⁢(K), δηλ f-1⁢(K)⊴G.

  4. iv.

    Έστω N≤G ώστε K⁢e⁢r⁢f≤N. Αν α∈N, τότε

    f⁢(α)∈f⁢(N)⇒α∈f-1⁢(f⁢(N)), (3.78)

    δηλ.

    N⊆f-1⁢(f⁢(N)). 3.3.1

    Έστω, τώρα, x∈f-1⁢(f⁢(N)). Τότε f⁢(x)∈f⁢(N), δηλ

    ∃α∈N:f⁢(x)=f⁢(α)⇒f⁢(x)⁢f⁢(α)-1=e⇒f⁢(x)⁢f⁢(α-1)=e⇒f⁢(x⁢α-1)=e⇒x⁢α-1∈K⁢e⁢r⁢f≤N⇒x⁢α-1∈N⇒x∈N⁢α=N. (3.79)

    Άρα

    f-1⁢(f⁢(N))⊆N. 3.3.2

    Από τις σχέσεις (3.3.1) και (3.3.2) προκύπτει το iv).

  5. v.

    Έστω N1,N2∈X και

    N1=N2⇒f⁢(N1)=f⁢(N2)≤H, (3.80)

    δηλ η F:A→B είναι συνάρτηση. Ας παρατηρήσουμε στο σημείο αυτό ότι η υπόθεση K⁢e⁢r⁢f≤Ni,i=1,2 δεν χρειάστηκε. Αν, τώρα, για N1,N2∈A ισχύει

    f⁢(N1)=f⁢(N2)⇒f-1⁢(f⁢(N1))=f-1⁢(f⁢(N2))⇒N1=N2, (3.81)

    εξ αιτίας του iv., δηλ. η F είναι αμφιμονότιμη συνάρτηση. Μένει να αποδείξουμε ότι η F είναι επί. Έστω Y∈B, τότε η f-1⁢(Y)≤G, λόγω του i., και f⁢(f-1⁢(Y))=Y, από τις ιδιότητες των συναρτήσεων και επειδή η f είναι επί συνάρτηση. Άρα F⁢(f-1⁢(Y))=Y, δηλ. η F είναι επί συνάρτηση και αποδείχθηκε το v). ■

Η επόμενη πρόταση περιγράφει τις υποομάδες μίας ομάδας πηλίκο. Το συμπέρασμα θα προκύψει ως εφαρμογή της Πρότασης 3.3.1.

Πρόταση 3.3.2

Έστω G μία ομάδα και N⊴G. Τότε κάθε υποομάδα της ομάδας G/N είναι της μορφής Κ/Ν όπου N≤K≤G. Επιπλέον

K/N⊴G/N⇔K⊴G. (3.82)

Απόδειξη. Θεωρούμε τον φυσικό ομομορφισμό f:G→G/N. Ο f είναι επιμορφισμός ομάδων, έτσι, σύμφωνα με το (v) της Πρότασης 3.3.1, έπεται ότι κάθε υποομάδα της ομάδας G/N είναι της μορφής f⁢(K) για κάποια υποομάδα Κ της G ώστε K⁢e⁢r⁢f≤G≤G. Όμως K⁢e⁢r⁢f=N, άρα f⁢(K)=K/N. Τέλος από τα ii) και iii) της Πρότασης 3.3.1, έπεται ότι

K/N⊴G/K⇔K⊴G. ■ (3.83)
Θεώρημα (Πρώτο Θεώρημα Ισομορφίας) 3.3.3

Έστω f:G→H ένας ομομορφισμός ομάδων. Τότε

G/K⁢e⁢r⁢f≅f⁢(G). (3.84)

Απόδειξη. Γνωρίζουμε ότι K⁢e⁢r⁢f⊴G (βλ. Πρόταση 3.2.15), άρα η G/K⁢e⁢r⁢f είναι ομάδα. Θεωρούμε την αντιστοιχία

F:G/K⁢e⁢r⁢f⟶f⁢(G),α⁢K⁢e⁢r⁢f⟼f⁢(α). (3.85)

Θα αποδείξουμε ότι η F είναι ισομορφισμός ομάδων. Έστω α,β∈G και

α⁢K⁢e⁢r⁢f=β⁢K⁢e⁢r⁢f⇔β-1⁢α∈K⁢e⁢r⁢f⇔f⁢(β-1⁢α)=e⇔f⁢(β-1)⁢f⁢(α)=e⇔f⁢(β)-1⁢f⁢(α)=e⇔f⁢(α)=f⁢(β)⇔F⁢(α⁢K⁢e⁢r⁢f)=F⁢(β⁢K⁢e⁢r⁢f). (3.86)

Άρα η F είναι αμφιμονότιμη συνάρτηση. Η F είναι επί, γιατί για το τυχαίο στοιχείο f⁢(g)∈f⁢(G), όπου g∈G, υπάρχει το g⁢K⁢e⁢r⁢f, ώστε F⁢(g⁢K⁢r⁢e⁢f)=f⁢(g). Τέλος η F είναι ομομορφισμός. Πράγματι, αν α,β∈G, τότε

F⁢(α⁢K⁢e⁢r⁢f⋅β⁢K⁢e⁢r⁢f)=F⁢(α⁢β⁢K⁢e⁢r⁢f)=f⁢(α⁢β)= (3.87)
=f(α)f(β)=F(αKerf)F(βKerf). (3.88)

Επομένως η F είναι ισομορφισμός ομάδων και

G/K⁢e⁢r⁢f≅f⁢(G).■ (3.89)
Θεώρημα 3.3.4

(Δεύτερο Θεώρημα Ισομορφίας ή Θεώρημα του παραλληλογράμμου) Έστω G μία ομάδα, N,K≤G και N⊴G. Τότε

K⁢N/N≅K/K∩N. (3.90)

Απόδειξη Παρατηρούμε ότι το γινόμενο ΚΝ είναι υποομάδα της G. Πράγματι αφού N⊴G έπεται ότι k⁢N=N⁢k, για κάθε k∈K. Οπότε K⁢N=N⁢K και από την Πρόταση 3.1.2, έπεται ότι K⁢N≤G. Η N⊴G, άρα είναι κανονική υποομάδα κάθε υποομάδας της G που περιέχει την ομάδα Ν. Επομένως N⊴K⁢N, έτσι η K⁢N/N είναι ομάδα. Θα χρησιμοποιήσουμε το Πρώτο Θεώρημα Ισομορφίας για να αποδείξουμε τον ζητούμενο ισομορφισμό. Παρατηρούμε ότι

K⁢N/N={k⁢η⁢N:k∈K,η∈N}={k⁢N:k∈K}. (3.91)

Θεωρούμε, τώρα, την αντιστοιχία

f:K⟶K⁢N/N,k⟼k⁢N. (3.92)

Η f είναι συνάρτηση. Πράγματι έστω k1,k2∈K και k1=k2, τότε k1⁢N=k2⁢N. Η f είναι επί συνάρτηση. Πράγματι έστω k⁢N ένα στοιχείο της K⁢N/N, τότε k∈K και f⁢(k)=k⁢N. Θα δείξουμε ότι η f είναι ομορφισμός ομάδων. Έστω k1,k2∈K, τότε

f⁢(k1⁢k2)=k1⁢k2⁢N=k1⁢N⁢k2⁢N=f⁢(k1)⁢f⁢(k2). (3.93)

Υπολογίζουμε τον πυρήνα K⁢e⁢r⁢f.

K⁢e⁢r⁢f={k∈K:k⁢N=N}={k∈K:k∈N}=K∩N. (3.94)

Τώρα, εφαρμόζουμε το Πρώτο Θεώρημα Ισομορφίας για τον επιμορφισμό f και έχουμε

K/K⁢e⁢r⁢f≅f⁢(K) (3.95)

δηλ

K/K∩N≅K⁢N/N.■ (3.96)
Παρατήρηση 3.3.5

Οι υποομάδες που εμφανίζονται στο Δεύτερο Θεώρημα Ισομορφίας έχουν το ακόλουθο διάγραμμα

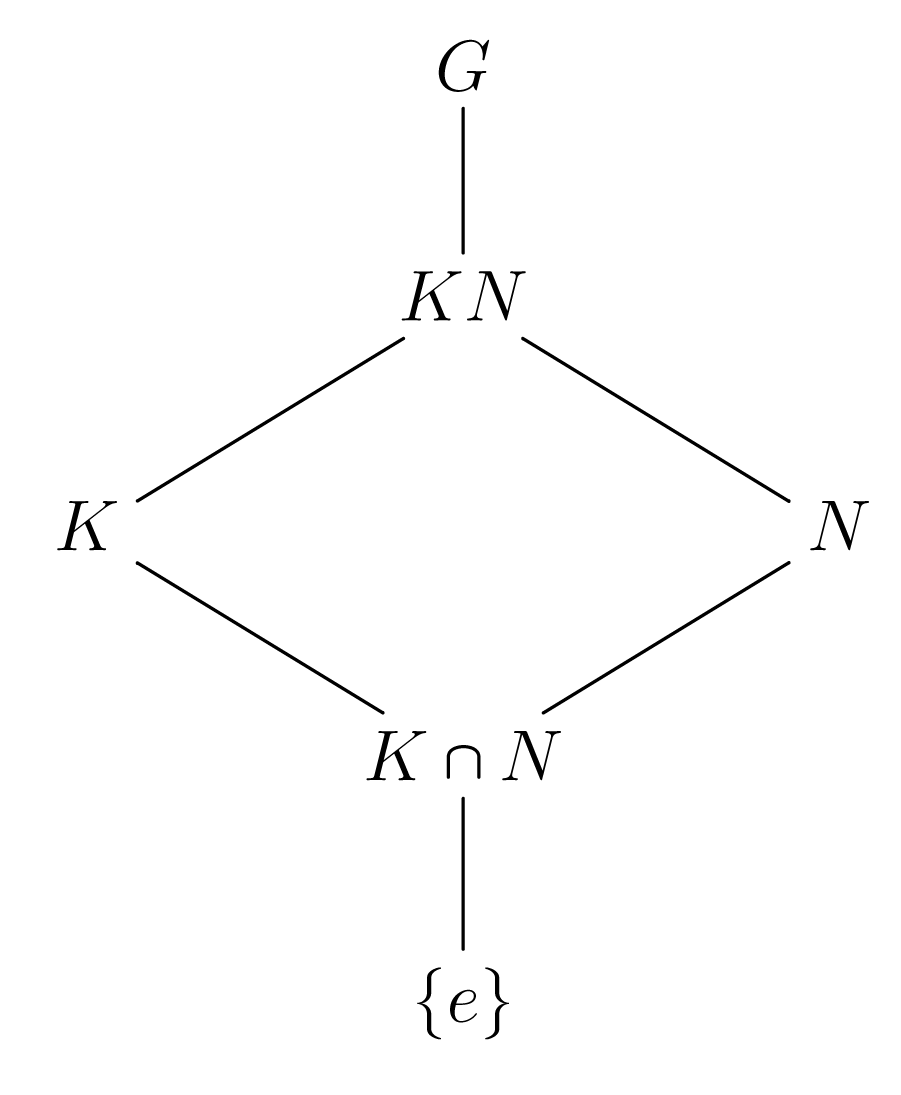Σχήμα 3.6

Εάν η K⊴G, τότε K⁢N/K≅N/K∩N. Έτσι παρατηρούμε ότι οι υποομάδες K⁢N,K,N,K∩N σχηματίζουν με το διάγραμμά τους ένα παραλληλόγραμμο που οι απέναντι πλευρές δηλώνουν ισόμορφες ομάδες. Γι’ αυτόν το λόγο το Δεύτερο Θεώρημα Ισομορφίας λέγεται και Θεώρημα του Παραλληλογράμμου. Δημιουργείται έτσι ένας μνημονικός κανόνας για το Δεύτερο Θεώρημα Ισομορφίας.

Θεώρημα (Τρίτο Θεώρημα Ισομορφίας) 3.3.6

Έστω G μία ομάδα, N⊴G, και H⊴G ώστε N≤H≤G. Τότε

(G/N)/(H/N)≅G/H. 3.3.4

Απόδειξη Θα εφαρμόσουμε και πάλι το Πρώτο Θεώρημα Ισομορφίας για την απόδειξη του ζητούμενου ισομορφισμού. Παρατηρούμε ότι από τις υποθέσεις που δίνονται οι G/N,H/N,G/H είναι ομάδες. Θεωρούμε την αντιστοιχία

f:G/N⟶G/H,g⁢N⟼g⁢H. (3.97)

Η διαδικασία που θα ακολουθήσουμε είναι αυτή του Δεύτερου Θεωρήματος Ισομορφίας, δηλ. αποδεικνύουμε ότι η f είναι επιμορφισμός ομάδων, υπολογίζουμε τον πυρήνα του και εφαρμόζουμε το Πρώτο Θεώρημα Ισομορφίας. Έστω g1⁢N,g2⁢N∈G/N και

g1⁢N=g2⁢N⇒g2-1⁢g1∈N≤H⇒g2-1⁢g1∈H⇒g1⁢H=g2⁢H, (3.98)

δηλ. η f είναι συνάρτηση. Έστω g⁢H∈G/H, τότε υπάρχει στοιχείο g⁢N∈G/N για το οποίο ισχύει f⁢(g⁢N)=g⁢H. Άρα η f είναι επί συνάρτηση. Έστω g1⁢N,g2⁢N∈G/N, τότε

f⁢(g1⁢N⁢g2⁢N)=f⁢(g1⁢g2⁢N)=g1⁢g2⁢H=g1⁢g2⁢H=g1⁢H⁢g2⁢H=f⁢(g1⁢N)⁢f⁢(g2⁢N). (3.99)

Άρα η f είναι ομομορφισμός ομάδων. Υπολογίζουμε τον K⁢e⁢r⁢f,

K⁢e⁢r⁢f={g⁢N∈G/N:f⁢(g⁢N)=H}={g⁢N∈G/N:g⁢H=H}= (3.100)
={gN∈G/N:g∈H}=H/N. (3.101)

Επομένως από το Πρώτο Θεώρημα Ισομορφίας έπεται ο ισομορφισμός 3.3.4.■

Παρατήρηση 3.3.7

Ο ισομορφισμός (3.3.4) θυμίζει σύνθετα κλάσματα. Φαίνεται ότι αν οι όροι των κλασμάτων ήταν αριθμοί, τότε το αποτέλεσμα θα ήταν ισότητα μεταξύ των κλασμάτων των δύο μελών. Έτσι μπορούμε να έχουμε ένα μνημονικό κανόνα για το Τρίτο Θεώρημα Ισομορφίας, αλλά το κυριότερο καταλαβαίνουμε γιατί έχει επιλεγεί ο όρος ((πηλίκο)) ως δεύτερος όρος για την ομάδα πηλίκο. Τα πηλίκα συμπεριφέρονται με ένα κοινό τρόπο στα μαθηματικά.

Θεώρημα (Τέταρτο Θεώρημα Ισομορφίας) 3.3.8

Έστω G μία ομάδα, N⊴G και f:G→G/N ο φυσικός επιμορφισμός. Η αντιστοιχία f του συνόλου των υποομάδων της G που περιέχουν την Ν και του συνόλου των υποομάδων της G/N με κανόνα K↦K/N είναι μία αμφιμονότιμη και επί συνάρτηση. Ακόμη αν Η,Κ είναι υποομάδες της G που περιέχουν τον Ν, τότε:

  1. i.

    H≤K αν και μόνον αν H/N≤K/N και τότε

    [K:H]=[K/N:H/N]. (3.102)
  2. ii.

    H⊴K αν και μόνον αν H/N⊴K/N και τότε

    K/H≅(K/N)/(H/N). (3.103)

Απόδειξη Για το πρώτο σκέλος του θεωρήματος εφαρμόζουμε την Πρόταση 3.3.1, v). Έτσι προκύπτει ότι η αντιστοιχία f είναι αμφιμονότιμη συνάρτηση. Για το επί της συνάρτησης f εφαρμόζουμε την Πρόταση 3.3.2. Κάθε υποομάδα της G/N είναι της μορφής Λ/N, όπου Λ≤G και N⊴Λ≤G. Άρα υπάρχει η υποομάδα Λ της G που έχει την ιδιότητα f⁢(Λ)=Λ/N, δηλ. η f είναι και επί συνάρτηση.
Για το δεύτερο σκέλος τώρα.

  1. i.

    Έστω ότι N≤H≤K και N⊴G, τότε ορίζονται οι ομάδες H/N και Κ/Ν, οι οποίες είναι υποομάδες της G/N και ακόμη από τον ορισμό τους H/N⊆K/N. Άρα H/N≤K/N.
    Ερχόμαστε, τώρα, στο δεύτερο μέλος του i). Εφόσον N≤H≤K, έστω

    K=⊍k∈X⁢k⁢H,H=⊍h∈Y⁢h⁢N 3.3.5

    όπου Χ είναι ένα πλήρες σύστημα αντιπροσώπων της Η στην Κ και Υ είναι ένα πλήρες σύστημα αντιπροσώπων της Ν στην υποομάδα Η, δηλ.

    K/H={k⁢H:k∈X}⁢ και ⁢H/N={h⁢N:h∈Y} 3.3.6

    Παρατηρούμε από τη σχέση (3.3.5) ότι

    K=⊍k∈X⁢k⁢(⊍h∈Y⁢h⁢N)=⊍k∈X,h∈Y⁢k⁢h⁢N (3.104)

    Θα αποδείξουμε ότι τα σύνολα k⁢h⁢N, για k∈X και h∈Y, είναι ξένα μεταξύ τους ανά δύο, δηλ. θα αποδείξουμε ότι

    K=⊍k∈X,h∈Y⁢k⁢h⁢N. 3.3.7

    Έστω k1,k2∈X με k1≠k2, δηλ. k1⁢H≠k2⁢H και h1,h2∈Y, με h1≠h2 δηλ. h1⁢N≠h2⁢N. Τότε, αν

    k1⁢h1⁢N=k2⁢h2⁢N⇒k2-1⁢k1⁢h1∈h2⁢N⇒k2-1⁢k1∈h2⁢N⁢h1-1⇒N⊂H, (3.105)

    γιατί N⊴G και N<H. Άρα k1⁢H=k2⁢H, αυτό, όμως, είναι αδύνατο από την επιλογή των k1,k2. Επόμένως αποδείξαμε τη σχέση (3.3.7). Ας εξετάσουμε τώρα το σύνολο πηλίκο (K/N)/(H/N). Από τη σχέση (3.3.7) έχουμε

    (K/N)/(H/N)={k⁢h⁢N⁢(H/N):k∈X⁢ και ⁢h∈Y}. (3.106)

    Έστω k∈X και h∈Y, τότε

    k⁢h⁢N⁢(H/N)=khN{h′N:h′∈Y}={khNh′N:h′∈Y}={khh′N:h′∈Y}=kN(H/N). (3.107)

    Άρα

    (Κ/Ν)/(Η/Ν)={k⁢N⁢(H/N):k∈X}. (3.108)

    Θεωρούμε, τώρα, την αντιστοιχία

    ϕ:K/H⟶(K/N)/(H/N),k⁢H⟼k⁢N⁢(H/N) 3.3.8

    λόγω των σχέσεων (3.3.6) και (3.3.8), η ϕ είναι μία αμφιμονότιμη και επί συνάρτηση, όπως μπορεί να αποδείξει με δουλειά ρουτίνας ο αναγνώστης. Επομένως

    [K:H]=[K/N:H/N] (3.109)

    και αποδείχθηκε το i).

  2. ii.

    Τα συμπεράσματα προκύπτουν αμέσως από την Πρόταση 3.3.2 και το Τρίτο Θεώρημα Ισομορφίας. ■

Παρατηρήσεις 3.3.9
  1. i.

    Το Θεώρημα 3.3.8 λέγεται επίσης Θεώρημα αντιστοιχίας (Corresponding Theorem).

  2. ii.

    Από το ii) του προηγούμενου θεωρήματος παρατηρούμε ότι

    K/H≅(K/N)/(H/N)=f⁢(K)/f⁢(H) (3.110)

    και

    f-1⁢(K/N)/f-1⁢(H/N)=K/H≅(K/N)/(H/N). (3.111)

Ας δουμε έναν ακόμη ενδιαφέροντα ισομορφισμό μεταξύ ομάδων πηλίκων υποομάδων μίας ομάδας G.

Θεώρημα 3.3.10

Έστω G μία ομάδα, N⊴G και H⊴L≤G. Τότε

L⁢N/H⁢N≅L/H⁢(L∩N). (3.112)

Απόδειξη Έστω f:G→G/N, ο φυσικός ομομορφισμός. Παρατηρούμε ότι

f⁢(L)={f⁢(l):l∈L}={l⁢N:l∈L}=L⁢N/N. (3.113)

Τώρα ορίζεται ο επιμορφισμός ομάδων

ϕ:=f|L:L⟶L⁢N/N,l⟼l⁢N, (3.114)

με K⁢e⁢r⁢ϕ={l:l⁢N=N}=L∩N, όπου f|L είναι ο περιορισμός της f στην υποομάδα L. Είναι εύκολο να δούμε ότι H⁢N⊴L⁢N, αφού N⊴G και H⊴L, δηλ. το L⁢N/H⁢N είναι ομάδα. Παρατηρούμε από το Τρίτο Θεώρημα Ισομορφίας, το Θεώρημα 3.3.8 και την Παρατήρηση 3.3.9 ii) ότι για τη συνάρτηση ϕ έχουμε

L⁢NH⁢N≅L⁢N/NH⁢N/N=ϕ⁢(L)ϕ⁢(H)≅ϕ-1⁢(ϕ⁢(L))ϕ-1⁢(ϕ⁢(H))≅Lϕ-1⁢(ϕ⁢(H)). 3.3.9

Θα αποδείξουμε ότι

ϕ-1⁢(ϕ⁢(Η))=H⁢(L∩N). 3.3.10

Έτσι αντικαθιστώντας την ϕ-1⁢(ϕ⁢(H)) από τη σχέση (3.3.10) στη σχέση (3.3.9) προκύπτει ο ζητούμενος ισομορφισμός ομάδων.
Για την απόδειξη της σχέσης (3.3.10), έστω x∈ϕ-1⁢(ϕ⁢(H)), τότε

ϕ⁢(x)∈ϕ⁢(H)⇒ϕ⁢(x)=ϕ⁢(h), για κάποιο, ⁢h∈H⇒ (3.115)
ϕ⁢(x⁢h-1)=e⇒x⁢h-1∈K⁢e⁢r⁢ϕ=L∩N⇒x∈H⁢(L∩N). (3.116)

Επομένως

ϕ-1⁢(ϕ⁢(H))⊆H⁢(L∩N). 3.3.11

Αν

x∈H⁢(L∩N)⇒ϕ⁢(x)∈ϕ⁢(H⁢(L∩N))=H⁢(L∩N)⁢N/N=H⁢N/N=ϕ⁢(H). (3.117)

Άρα ϕ⁢(x)∈ϕ⁢(H)⇒x∈ϕ-1⁢(ϕ⁢(H)),x∈H⁢(L∩N). Επομένως

H⁢(L∩N)⊆ϕ-1⁢(ϕ⁢(H)). 3.3.12

Από τις σχέσεις (3.3.11) και (3.3.12) έπεται η σχέση (3.3.10). ■

Ασκήσεις

1. Έστω G μία ομάδα και N,K<G με N⊴G. Να αποδείξετε ότι

  1. i.

    K∩N⊴K,

  2. ii.

    η αντιστοιχία

    ϕ:K⁢N/N⟶K/K∩N,k⁢N⟼k⁢(K∩N) (3.118)

    είναι ισομορφισμός ομάδων. Έτσι προκύπτει μία άλλη απόδειξη για το Δεύτερο Θεώρημα Ισομορφίας.

2. Έστω G μία ομάδα, H⊴G και ϕ:G→G/H ο φυσικός ομομορφισμός. Να αποδείξετε τα επόμενα:

  1. i.

    H≤T≤S≤G⇔T/H≤S/H.

  2. ii.

    [S:T]=[S/H:T/H].

  3. iii.

    H≤T⊴S≤G⇒S/T≅(S/H)/(T/H).

3. Έστω G μία ομάδα, H⊴G,[G:H]<∞,N≤G,|N|<∞ και ([G:H],|N|)=1. Να αποδείξετε ότι N≤H.
4. Έστω G μία ομάδα, H⊴G και N≤G έτσι ώστε |H|>∞,[G:N]<∞ και ([G:H],|H|)=1. Να αποδείξετε ότι H≤N.
5. Έστω G μία ομάδα και H⊴G τέτοια, ώστε (|H|,[G:H])=1. Να αποδείξετε ότι η Η είναι η μοναδική υποομάδα της G με τάξη |H|.
6. Μία υποομάδα Η της ομάδας G λέγεται μέγιστη κανονική υποομάδα (maximal normal subgroup), αν H⊴G και δεν υπάρχει κανονική υποομάδα Κ της G τέτοια, ώστε Η≨K≨G. Να αποδείξετε ότι η Η είναι μέγιστη κανονική υποομάδα της G αν και μόνον αν είναι απλή (simple), δηλ. δεν περιέχει γνήσια μη τετριμμένη κανονική υποομάδα.

3.4 Σχέσεις ορισμού και παράσταση ομάδας

Μία ομάδα G ορίζεται από το σύνολό της και τον τρόπο που πολλαπλασιάζονται τα στοιχεία μεταξύ τους. Αν θεωρήσουμε μία κυκλική ομάδα G=⟨α⟩ τάξης n<∞. Τότε αn=e και η σχέση αυτή είναι αρκετή για να προσδιορίσουμε το σύνολο G και να υπολογίσουμε τον πίνακα Cayley της G. Για την αφηρημένη διεδρική ομάδα D2⁢n (Ορισμός 3.1.15) γνωρίζουμε ότι παράγεται από τα στοιχεία α,β που ικανοποιούν τις

αn=e,β2=e,(αk⁢β)2=2,  1≤k≤n-1. 3.4.1

Παρατηρούμε ότι

(α⁢β)2=e⇒β⁢α=α-1⁢β

και

(α2⁢β)2=α2⁢β⁢α⁢α⁢β=α2⁢α-1⁢β⁢α⁢β=(α⁢β)2=e

και όμοια ισχύει

(αk⁢β)2=e, για ⁢3≤k≤n-1.

Έτσι οι σχέσεις 3.4.1 μπορούν να γραφούν ως

αn=e=β=(α⁢β)2 3.4.2

και αρκούν προκειμένου να αναγράψουμε τα στοιχεία της D2⁢n και του πίνακα Cayley αυτής, όπως ο αναγνώστης με πράξεις μπορεί να διαπιστώσει. Ένα σύνολο, έστω r1,r2,…,rn, εξισώσεων που ικανοποιούν τα στοιχεία ενός τυχόντος συνόλου, S, μίας ομάδας G τέτοιες ώστε από αυτές να μπορούν να προκύψουν όλα τα στοιχεία της G λέγονται σχέσεις ορισμού (defining relations) της G. Το σύνολο S των παραγόντων στοιχείων με τις σχέσεις ορισμού r1,r2,…,rn αποτελούν την παράσταση (presentation) της ομάδας G και συμβολίζεται ως

G=S|r1,r2,…,rn.

Έτσι η κυκλική ομάδα G τάξης n<∞ που παράγεται από το στοιχείο α έχει παράσταση

G=α|αn=e.

Η (αφηρημένη) διεδρική ομάδα D2⁢n έχει παράσταση:

D2⁢n=α,β|α2=e=β2=(α⁢β)2.

Η τετραδική ομάδα Q8 (βλ. Παράδειγμα 3.1.13.4) έχει παράσταση

Q8=i,j|i4=1=j4,j⁢i=i3⁢j,i2=j2.

Ας θεωρήσουμε την κυκλική ομάδα G άπειρης τάξης που παράγεται από το στοιχείο g. Παρατηρούμε ότι το στοιχείο g δεν ικανοποιεί καμία εξίσωση, έτσι η παράσταση της ομάδας αυτής είναι ⟨g⟩. Είναι, επομένως, δυνατόν να μην υπάρχουν σχέσεις ορισμού για μία ομάδα. Μία ομάδα F που παράγεται από ένα σύνολο S και δεν υπάρχει καμία σχέση μεταξύ των στοιχείων του S λέγεται ελεύθερη (free) ομάδα παραγόμενη από το S. Έτσι η ελεύθερη ομάδα, που παράγεται από το στοιχείο g, είναι κυκλική ομάδα ⟨g⟩ άπειρης τάξης. Η ελεύθερη ομάδα ⟨α,β⟩ είναι μία ομάδα άπειρης τάξης που όλα τα στοιχεία της είναι της μορφής α,αi,βj,α⁢β,α⁢β⁢α,α⁢β⁢α⁢β,β⁢α⁢β κ.ο.κ. Συνήθως τα στοιχεία μίας ελεύθερης ομάδας λέγονται λέξεις (words). Δεν θα επεκταθούμε σε αυτό το βιβλίο περισσότερο για τις ελεύθερες ομάδες. Αυτές αποτελούν ένα σημαντικό θέμα της θεωρίας ομάδων και από αυτές μέσω ομομορφισμών προκύπτουν όλες οι ομάδες. Εδώ ακολουθήσαμε την αντίστροφη διαδικασία ως διαισθητικότερη για τον πρωτοεισαγόμενο αναγνώστη στη θεωρία ομάδων. Ας επανέλθουμε στην παράσταση

G=S|r1,r2,…,rn 3.4.3

μίας ομάδας G. Όταν γνωρίζουμε την ομάδα G, όπως π.χ. τις D2⁢n,Q8,Sn, Mn⁢(ℚ), G⁢Ln⁢(ℤp), τότε μπορούμε να βρούμε ένα σύνολο παραγόντων στοιχείων και ένα σύνολο σχέσεων ορισμού. Αυτό δεν είναι βέβαια εύκολο και κυρίως όταν ενδιαφερόμαστε για κατά το δυνατόν μικρότερα τέτοια σύνολα. Το αντίστροφο, όμως, πρόβλημα είναι δυσεπίλυτο και μερικές φορές άλυτο, δηλ. αν έχουμε την παράσταση (3.4.3) μπορούμε να βρούμε τη δομή αυτής της ομάδας; Μπορούμε να αποδείξουμε αν G≠{e}; Μπορούμε να διακρίνουμε πότε δύο στοιχεία της G είναι ίσα; Μπορούμε από τις παραστάσεις των ομάδων να διαπιστώσουμε αν είναι ισόμορφες; Αυτά τα ερωτήματα δεν έχουν απαντηθεί πλήρως. Η σχετική, όμως, έρευνα έχει οδηγήσει την εξέλιξη των υπολογιστικών μηχανών. Ο ενδιαφερόμενος αναγνώστης μπορεί να ξεκινήσει τη μελέτη του από τα [C-M], [MKS], [Rob], [Rot].