Κεφάλαιο 1Βασικές Έννοιες
1.1 Ορισμός ομάδας - Παραδείγματα
Συχνά στα μαθηματικά μας ενδιαφέρει να εξετάσουμε αν κάποια φαινόμενα που ισχύουν σε αριθμητικά συστήματα ισχύουν σε ένα γενικότερο περιβάλλον, όπως π.χ. σε τυχαία σύνολα. Για την έννοια της ομάδας ένα ερώτημα αφετηρίας είναι πώς γενικεύεται η αριθμητική δομή όταν στη θέση του συνόλου των ακέραιων είναι ένα τυχαίο σύνολο και στη θέση της πρόσθεσης μία τυχαία πράξη; Θα μπορούσε να μας ενδιαφέρει ένα τέτοιο επίτευγμα;
Γνωρίζουμε τις ιδιότητες της πρόσθεσης στο από τις πρώτες ενασχολήσεις μας με την αριθμητική, έτσι ας ασχοληθούμε με το πρώτο από τα δύο παραπάνω ερωτήματα. Το δεύτερο θα μας απασχολεί συνεχώς σε αυτό το κείμενο και θα έχουμε απαντήσεις.
Για τις έννοιες που δεν αναφέρονται εδώ ο αναγνώστης παραπέμπεται στα Παραρτήματα.
Ορισμός 1.1.1
Έστω ένα μη κενό σύνολο εφοδιασμένο με μία πράξη . Η αλγεβρική δομή λέγεται ομάδα (group) αν ισχύουν οι επόμενες ιδιότητες:
-
i.
Η πράξη είναι προσεταιριστική (associative), δηλαδή
(1.1) για όλα τα στοιχεία .
-
ii.
Υπάρχει ένα στοιχείο, έστω , στο τέτοιο ώστε
(1.2) για κάθε . Το στοιχείο λέγεται ουδέτερο ή ταυτοτικό στοιχείο (neutral or identity) της .
-
iii.
Αν , υπάρχει ένα στοιχείο ώστε
(1.3) Το στοιχείο λέγεται αντίστροφο (inverse) του .
Ιδιαίτερα αν η πράξη είναι αντιμεταθετική, δηλαδή αν
| (1.4) |
για όλα τα , τότε η ομάδα λέγεται αντιμεταθετική (commutative) ή αβελιανή (abelian) ή ομάδα του Abel.
Ο συμβολισμός του αντίστροφου στοιχείου προέρχεται από τον συμβολισμό του αντίστροφου στοιχείου στις αριθμητικές δομές. Αν η πράξη της ομάδας συμβολίζεται με ονομάζεται πρόσθεση (addition). Σε αυτήν την περίπτωση το ουδέτερο στοιχείο λέγεται μηδενικό (zero) και συμβολίζεται με , ενώ το αντίστροφο του λέγεται αντίθετο (opposite) και συμβολίζεται . Αν η πράξη λέγεται πολλαπλασιασμός (multiplication), τότε συμβολίζεται με όπως στις αριθμητικές δομές και το ουδέτερο στοιχείο λέγεται επίσης μοναδιαίο (unit). Θα συμβολίζουμε με το ουδέτερο στοιχείο για τις πολλαπλασιαστικές δομές. Για τα συγκεκριμένα παραδείγματα όπως οι αριθμητικές δομές ή τα σύνολα πινάκων ή συναρτήσεων θα χρησιμοποιούμε τους γνωστούς και καθιερωμένους συμβολισμούς για το αντίστροφο, το αντίθετο, το μοναδιαίο ή το μηδενικό στοιχείο. Αυτό γίνεται σαφές στα παραδείγματα που ακολουθούν.
Παραδείγματα 1.1.2
Οι αριθμητικές δομές , , , είναι αβελιανές (προσθετικές) ομάδες.
Συμβολίζουμε με και ανάλογα , . Εύκολα βλέπουμε ότι οι αριθμητικές δομές , , είναι αβελιανές (πολλαπλασιαστικές) ομάδες. Ενώ οι αριθμητικές δομές , δεν είναι ομάδες.
Έστω , παρατηρούμε ότι η είναι μία αβελιανή ομάδα, ενώ η δεν είναι ομάδα.
Έστω , φυσικοί αριθμοί και ένα μη κενό σύνολο. Θυμίζουμε ότι με τον όρο -πίνακας (matrix) με συντελεστές από το εννοούμε μία συνάρτηση
| (1.5) |
και τον συμβολίζουμε με
| (1.6) |
Με συμβολίζουμε το σύνολο των -πινάκων , με για και . Η αλγεβρική δομή είναι μία αβελιανή ομάδα, όπου με συμβολίζουμε το άθροισμα των -πινάκων, δηλαδή αν τότε
| (1.7) |
Το μηδενικό στοιχείο της είναι ο μηδενικός -πίνακας , δηλαδή αυτός για τον οποίο , για και . Αντίθετος του πίνακα είναι ο πίνακας , δηλαδή .
Ανάλογα οι αλγεβρικές δομές , , είναι προσθετικές αβελιανές ομάδες.
Συμβολίζουμε με το σύνολο των -πινάκων με συντελεστές από το σύνολο . Παρατηρούμε ότι η , όπου , είναι επίσης μία προσθετική αβελιανή ομάδα.
Έστω . Συμβολίζουμε με
| (1.8) |
όπου με συμβολίζουμε την ορίζουσα του πίνακα . Από τη Γραμμική ’λγεβρα γνωρίζουμε ότι αν για τον πίνακα ισχύει , τότε και μόνον τότε ορίζεται ο αντίστροφος πίνακας για τον οποίο ισχύουν οι σχέσεις και
| (1.9) |
όπου με συμβολίζουμε τον λεγόμενο μοναδιαίο (unit) -πίνακα, δηλαδή αυτόν που όλα τα στοιχεία του πάνω στην κύρια διαγώνιο ισούνται με και όλα τα άλλα στοιχεία του είναι ίσα με μηδέν.
Παρατηρούμε αμέσως ότι το σύνολο με πράξη τον πολλαπλασιασμό πινάκων αποτελεί ομάδα με μοναδιαίο στοιχείο το και αντίστροφο του τον πίνακα . Η ομάδα , για , δεν είναι αβελιανή, αφού δεν ισχύει πάντα η αντιμεταθετικότητα των πινάκων, δηλαδή, δεν ισχύει
| (1.10) |
για όλα τα . Η λέγεται γενική γραμμική ομάδα (general linear group).
Ας θεωρήσουμε ένα μη κενό σύνολο και το σύνολο όλων των συναρτήσεων . Συμβολίζουμε, ως συνήθως, με τη σύνθεση συναρτήσεων. Είναι φανερό ότι η σύνθεση συναρτήσεων στο ορίζεται και ότι έχει την προσεταιριστική ιδιότητα. Έτσι η είναι μία αλγεβρική δομή. Από τη θεωρία των συναρτήσεων γνωρίζουμε ότι η ταυτοτική συνάρτηση στο σύνολο έχει την ιδιότητα
| (1.11) |
δηλαδή η είναι ουδέτερο στοιχείο της . Είναι η ομάδα; Για να συμβαίνει αυτό θα πρέπει, για κάθε στοιχείο , να υπάρχει μία συνάρτηση έτσι ωστε . Γνωρίζουμε, όμως, από τη θεωρία συναρτήσεων ότι η ύπαρξη μίας τέτοιας συνάρτησης ισοδυναμεί με το γεγονός ότι η είναι αμφιμονότιμη και επί συνάρτηση. Όμως, κάθε συνάρτηση δεν έχει αυτές τις ιδιότητες. Επομένως η δεν μπορεί να είναι ομάδα.
Συμβολίζουμε με το σύνολο των αμφιμονότιμων και επί συναρτήσεων του συνόλου . Βέβαια . Το λέγεται σύνολο των μετασχηματισμών (transformations) του συνόλου . Είναι εύκολο να διαπιστώσουμε ότι η αλγεβρική δομή είναι ομάδα με τη συνάρτηση να είναι ουδέτερο στοιχείο και την αντίστροφη συνάρτηση της να είναι το αντίστροφο στοιχείο της . Βέβαια η ομάδα δεν είναι αντιμεταθετική, αφού η σύνθεση συναρτήσεων (όταν αυτή ορίζεται) δεν έχει πάντα την αντιμεταθετική ιδιότητα.
Η ομάδα λέγεται ομάδα μετασχηματισμών (transformation group) του συνόλου και, όπως θα διαπιστώσουμε από την ανάπτυξη της θεωρίας ομάδων, παίζει εξαιρετικά ενδιαφέροντα ρόλο τόσο για τη θεωρία ομάδων όσο και για τις εφαρμογές της σε άλλους επιστημονικούς κλάδους.
Οι ομάδες μετασχηματισμών είναι από τις βασικές ομάδες που εμφανίζονται στις εφαρμογές της θεωρίας ομάδων. Το ο Felix Klein ανακοίνωσε το Erlangen Program σύμφωνα με το οποίο επιχειρούσε να ταξινομήσει τις γεωμετρίες χρησιμοποιώντας τη σημασία των ομάδων μετασχηματισμών.
Το ενδιαφέρον της Γεωμετρίας για τις ομάδες μετασχηματισμών εμφανίζεται όταν το σύνολο είναι το σύνολο των σημείων κάποιου γεωμετρικού αντικειμένου π.χ. της πραγματικής ευθείας, του επιπέδου, της σφαίρας κ.ο.κ.
Παρατηρούμε ότι κάθε στοιχείο της ομάδας ικανοποιεί τη σχέση , όμως δε συμβαίνει , , εκτός αν η είναι η ταυτοτική συνάρτηση. Γι’ αυτόν τον λόγο κάθε στοιχείο της λέγεται συμμετρία (symmetry) του και η ομάδα ομάδα των συμμετριών του (group of symmetries of X). Στα παραδείγματα 1.1.4 θα δούμε συγκεκριμένες περιπτώσεις.
Ας θεωρήσουμε το σύνολο . Τότε το σύνολο είναι ακριβώς το σύνολο των αμφιμονότιμων και επί συναρτήσεων του συνόλου στον εαυτό του, δηλαδή το σύνολο των μεταθέσεων των αντικειμένων . Η ομάδα σε αυτήν την περίπτωση λέγεται ομάδα μεταθέσεων (permutation group) των αντικειμένων και συμβολίζεται με . Τα αντικείμενα τα συμβολίζουμε με τους αριθμούς για να απλουστευτεί ο συμβολισμός.
Είναι εύκολο να αποδείξουμε ότι το πλήθος των στοιχείων του συνόλου είναι . Ένα στοιχείο της συμβολίζεται αναλυτικότερα
| (1.12) |
όπου είναι η εικόνα του μέσω της . Αν , τότε το γινόμενο και απλούστερα είναι η σύνθεση των συναρτήσεων , . Έτσι , . Το αντίστροφο του είναι το
| (1.13) |
Στο σημείο αυτό ας παρατηρήσουμε ότι το στοιχείο θα μπορούσε να γραφτεί κατά τους ισοδύναμους τρόπους:
| (1.14) |
κ.ο.κ.. Αν
| (1.15) |
τότε το είναι το
| (1.16) |
Ιδιαίτερα υπολογίζουμε ότι
| (1.17) |
| (1.18) |
Το παράδειγμα που θα παρουσιάσουμε τώρα είναι από το σύνολο των μιγαδικών αριθμών. Αν είναι ένας συγκεκριμένος πρώτος ακέραιος αριθμός, ορίζουμε
| (1.19) |
Παρατηρούμε ότι ο αριθμός εξαρτάται από τον . Το σύνολο με πράξη τον συνήθη πολλαπλασιασμό των μιγαδικών αριθμών αποτελεί αντιμεταθετική ομάδα. Πράγματι:
Αν , τότε υπάρχουν φυσικοί αριθμοί , τέτοιοι ωστε
| (1.20) |
όπου είναι ο μεγαλύτερος από τους . Αυτό σημαίνει ότι , δηλαδή ο πολλαπλασιασμός είναι πράξη στο .
. Αφού έπεται ότι ο πολλαπλασιασμός στο διατηρεί τις ιδιότητες που έχει στο . Έτσι η πράξη στο είναι προσεταιριστική και αντιμεταθετική.
. Είναι φανερό ότι .
. Αν , τότε θα υπάρχει φυσικός αριθμός τέτοιος ώστε . Τότε, όμως,
| (1.21) |
Άρα και .
Από τα έπεται ότι το είναι αβελιανή ομάδα. Η λέγεται σχεδόν κυκλική ομάδα (almost cyclic group).
Το σύνολο των κλάσεων υπολοίπων , και , είναι το επόμενο παράδειγμα που θα μας απασχολήσει. Χωρίς μαθηματική αυστηρότητα μπορούμε να περιγράψουμε το ως εξής: Το σύνολο είναι ένα σύνολο με στοιχεία σύνολα. Σε κάθε στοιχείο του ανήκουν όλοι οι ακέραιοι αριθμοί που διαιρούμενοι δια του αφήνουν το ίδιο υπόλοιπο. Αν είναι αυτό το υπόλοιπο, τότε το στοιχείο αυτό του το συμβολίζουμε με . Τα δυνατά υπόλοιπα που παρουσιάζονται, αν διαιρέσουμε κάθε ακέραιο δια του , είναι . Έτσι
| (1.22) |
όπου , κ.ο.κ.
Θα κατασκευάσουμε, τώρα, το . Στο σύνολο ορίζουμε τη σχέση
| (1.23) |
Η σχέση αυτή είναι σχέση ισοδυναμίας. (Να αποδειχθεί ως άσκηση). Συμβολίζουμε με την κλάση που ανήκει ο ακέραιος αριθμός . Το σύνολο των κλάσεων ισοδυναμίας που χωρίζει αυτή η σχέση ισοδυναμίας το , δηλαδή το σύνολο πηλίκο , το συμβολίζουμε με . Έτσι
| (1.24) |
Από τις ιδιότητες των σχέσεων ισοδυναμίας ισχύουν οι σχέσεις
-
i.
.
-
ii.
ή , για .
Είναι φανερό ότι
| (1.25) |
Από την άλλη μεριά, όμως, αφού
| (1.26) |
έπεται ότι
| (1.27) |
Από τις παραπάνω σχέσεις προκύπτει ότι
| (1.28) |
Στο σύνολο ορίζουμε την πρόσθεση ως εξής:
| (1.29) |
Θα αποδείξουμε ότι η είναι συνάρτηση, δηλαδή η είναι πράξη στο . Αν , τότε και . Άρα και όμοια , για κάποιους ακεραίους . Έτσι και . Επομένως η είναι πράξη στο .
Όμοια μπορεί να αποδειχθεί ότι ο πολλαπλασιασμός
| (1.30) |
είναι πράξη στο .
Εξετάζουμε τώρα τις ιδιότητες των πράξεων αυτών στο .
1. Αν , τότε
| (1.31) |
δηλαδή η πρόσθεση στο είναι προσεταιριστική.
2. Αν , τότε , δηλαδή το είναι μηδενικό στοιχείο.
3. Αν , τότε , δηλαδή το , η κλάση με αντιπρόσωπο το , είναι αντίθετο του .
4. Αν , τότε , δηλαδή η πρόσθεση είναι αντιμεταθετική πράξη.
Όμοια μπορούν να αποδειχθούν οι ιδιότητες
5. Αν , τότε .
6. Αν , τότε .
7. Αν , τότε .
Από τα παραπάνω καταλήγουμε στο επόμενο συμπέρασμα.
Συμπέρασμα: Η είναι αντιμεταθετική ομάδα, ενώ η δεν είναι ομάδα.
Θεωρούμε το σύνολο . Είναι φανερό ότι . Τα στοιχεία του λέγονται πρώτες κλάσεις υπολοίπων modn (prime classes modn). Ο πολλαπλασιασμός στο εξακολουθεί να είναι πράξη στο . Πράγματι: Αν , είναι ακέραιοι αριθμοί τέτοιοι ώστε και , τότε είναι γνωστό ότι . Άρα, αν , τότε .
Ο πολλαπλασιασμός στο είναι προσεταιριστική και αντιμεταθετική πράξη, αφού αυτό συμβαίνει στο . Ακόμη, είναι φανερό ότι αφού .
Θα δείξουμε, τώρα, ότι κάθε στοιχείο του έχει αντίστροφο στο . Αν , τότε για κάποιους ακεραίους . Έτσι . Όμως, γιατί για τους ακέραιους ισχύει . Άρα η είναι η αντίστροφη κλάση της . Αποδείχθηκε, επομένως, ότι η είναι αβελιανή ομάδα.
Ένα εύλογο ερώτημα είναι αν και πότε συμβαίνει . Παρατηρούμε ότι αν ο είναι σύνθετος ακέραιος, δηλαδή έχει μία ανάλυση , , , τότε υπάρχουν στοιχεία του που δεν ανήκουν στο , π.χ. . Άρα . Αν , όπου είναι πρώτος φυσικός αριθμός, τότε είναι φανερό ότι , αφού , για . Καταλήγουμε, λοιπόν, στο συμπέρασμα:
Συμπέρασμα: Έστω . Ικανή και αναγκαία συνθήκη για να ισχύει , είναι ο να είναι πρώτος φυσικός αριθμός.
Έστω δύο ομάδες. Σχηματίζουμε το καρτεσιανό γινόμενο
Στο σύνολο ορίζουμε την πράξη
| 1.1.1 |
όπου
Είναι εύκολο να αποδείξουμε ότι η πράξη αυτή στο είναι προσεταιριστική. Ακόμη αν είναι το ουδέτερο στοιχείο της , τότε το στοιχείο είναι το ουδέτερο στοιχείο του . Πράγματι
και
Άρα το είναι το ουδέτερο στοιχείο του Αν τότε βλέπουμε ότι
και
Άρα το είναι το αντίστροφο του , δηλ.
Από τα παραπάνω προκύπτει ότι το με την πράξη (1.1.1) είναι ομάδα. Η ομάδα είναι αβελιανή αν και μόνον αν η και η είναι αβελιανές ομάδες. Ο αναγνώστης καλείται να αποδείξει την αλήθεια αυτής της πρότασης. Ας θεωρήσουμε, τώρα, έναν φυσικό αριθμό και έστω
το καρτεσιανό γινόμενο των ομάδων Ανάλογα με την ομάδα , μπορούμε να δώσουμε στο τη δομή μίας ομάδας. Πράγματι ορίζουμε στο την πράξη:
όπου για Η πράξη αυτή είναι προσεταιριστική, όπως καλείται να αποδείξει ο αναγνώστης. Ακόμη, αν είναι το ουδέτερο στοιχείο της το είναι το ουδέτερο στοιχείο του . Επίσης το είναι αντίστροφο στοιχείο του δηλ.
Ο αναγνώστης καλείται να εκτελέσει τις απαιτούμενες πράξεις. Έτσι το με αυτήν την πράξη είναι ομάδα.
Η ομάδα λέγεται ευθύ εξωτερικό γινόμενο (external direct product) των ομάδων
Από τα παραδείγματα που προηγήθηκαν διαπιστώνουμε ότι η έννοια της ομάδας συναντάται πολύ συχνά στα μαθηματικά. Πριν προχωρήσουμε σε περισσότερα παραδείγματα αλλά και σε ιδιότητες των ομάδων, θα σχολιάσουμε τον ορισμό της ομάδας και συγκεκριμένα θα μας απασχολήσει η μοναδικότητα ή μη του ουδέτερου στοιχείου μίας ομάδας και η μοναδικότητα ή μη του αντίστροφου στοιχείου ενός στοιχείου . Βέβαια οι πληροφορίες αυτές δεν προσφέρονται αμέσως από τον ορισμό της ομάδας. Ο ορισμός της ομάδας απαιτεί την ύπαρξη αυτών των στοιχείων, η μοναδικότητα θα απαιτήσει λίγο κόπο, όπως θα δούμε αμέσως.
Πρόταση 1.1.3
Έστω μία ομάδα. Η έχει μοναδικό ουδέτερο στοιχείο και κάθε στοιχείο έχει μοναδικό αντίστροφο στοιχείο.
Απόδειξη: Έστω και δύο ουδέτερα στοιχεία της , τότε
| (1.32) |
αφού το είναι ουδέτερο στοιχείο της , και
| (1.33) |
αφού το είναι ουδέτερο στοιχείο της . Άρα , δηλαδή το ουδέτερο στοιχείο της είναι μοναδικό.
Έστω, τώρα, ότι είναι αντίστροφα στοιχεία του στοιχείου . Τότε
| (1.34) |
αφού η είναι συνάρτηση. Όμως, η είναι προσεταιριστική πράξη, έτσι από την τελευταία σχέση και τον ορισμό της ομάδας προκύπτει ότι
| (1.35) |
Άρα κάθε στοιχείο της ομάδας έχει μοναδικό αντίστροφο στοιχείο.
Έστω μία ομάδα και ας υποθέσουμε ότι , δηλαδή το σύνολο είναι πεπερασμένο. Μπορούμε να γράψουμε τα πλήθους στοιχεία , , σχηματίζοντας τον ακόλουθο πίνακα
Πίνακας 1.1
όπου στη θέση -γραμμή και -στήλη τοποθετούμε το στοιχείο . Έτσι τα στοιχεία κάθε γραμμής και κάθε στήλης του παραπάνω πίνακα ανήκουν στο σύνολο . Ο πίνακας αυτός λέγεται πίνακας Cayley της ομάδας G (multiplication Cayley table or multiplication table of G). Από τον πίνακα Cayley της ομάδας μπορούν να διαπιστωθούν διάφορες ιδιότητες της ομάδας. Π.χ. αν η ομάδα είναι αβελιανή, τότε ο πίνακας των στοιχείων είναι συμμετρικός ως προς την κύρια διαγώνιο που σχηματίζουν τα στοιχεία , , αλλά ισχύει και το αντίστροφο. Βέβαια αν το σύνολο έχει μεγάλο πλήθος στοιχείων, τότε ο πίνακας Cayley της δεν είναι πρακτικός.
Με τον ίδιο τρόπο μπορούμε να δημιουργήσουμε τον πίνακα Cayley για την τυχούσα αλγεβρική δομή , χωρίς απαραίτητα να είναι ομάδα.
Παραδείγματα 1.1.4
Θεωρούμε το υποσύνολο του συνόλου των μιγαδικών αριθμών, δηλαδή , και την αλγεβρική δομή με πράξη τον πολλαπλασιασμό των μιγαδικών αριθμών. Είναι εύκολο να διαπιστώσουμε ότι η είναι αβελιανή ομάδα με πίνακα Cayley τον ακόλουθο Πίνακα 1.2
Πίνακας 1.2
Έστω , τότε το σύνολο , όπου τα στοιχεία ,,, είναι οι συναρτήσεις που περιγράφονται από τον Πίνακα 1.3
Πίνακας 1.3
Η αλγεβρική δομή με πράξη τη σύνθεση συναρτήσεων είναι ημιομάδα, αφού η είναι προσεταιριστική. Ο πίνακας Cayley της είναι ο ακόλουθος
Πίνακας 1.4
Από το Παράδειγμα 1.1.2.6 η δεν είναι ομάδα. Παρατηρώντας ότι μόνον οι είναι αμφιμονότιμες και επί, το με είναι ομάδα με πίνακα Cayley
Πίνακας 1.5
Θεωρούμε ένα ισόπλευρο τρίγωνο με κορυφές , , και κέντρο Ο όπως στο σχήμα:
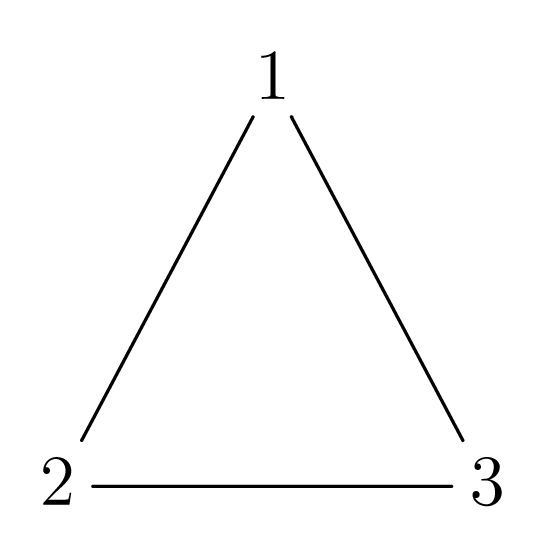 Σχήμα 1.1
Σχήμα 1.1Ας καλέσουμε το σύνολο των σημείων του επιπέδου που περικλείονται από τις πλευρές του τριγώνου. Έστω η στροφή ως προς το κέντρο του Ο του τριγώνου κατά γωνία με φορά αντίστροφη των δεικτών του ρολογιού. Βέβαια η στροφή είναι μία συνάρτηση από το στο η οποία είναι φανερό ότι είναι αμφιμονότιμη και επί, δηλαδή . Όμως, κάθε σημείο του δεν μένει στη θέση του π.χ. , , . Ας συμβολίσουμε ως ακολούθως
| (1.36) |
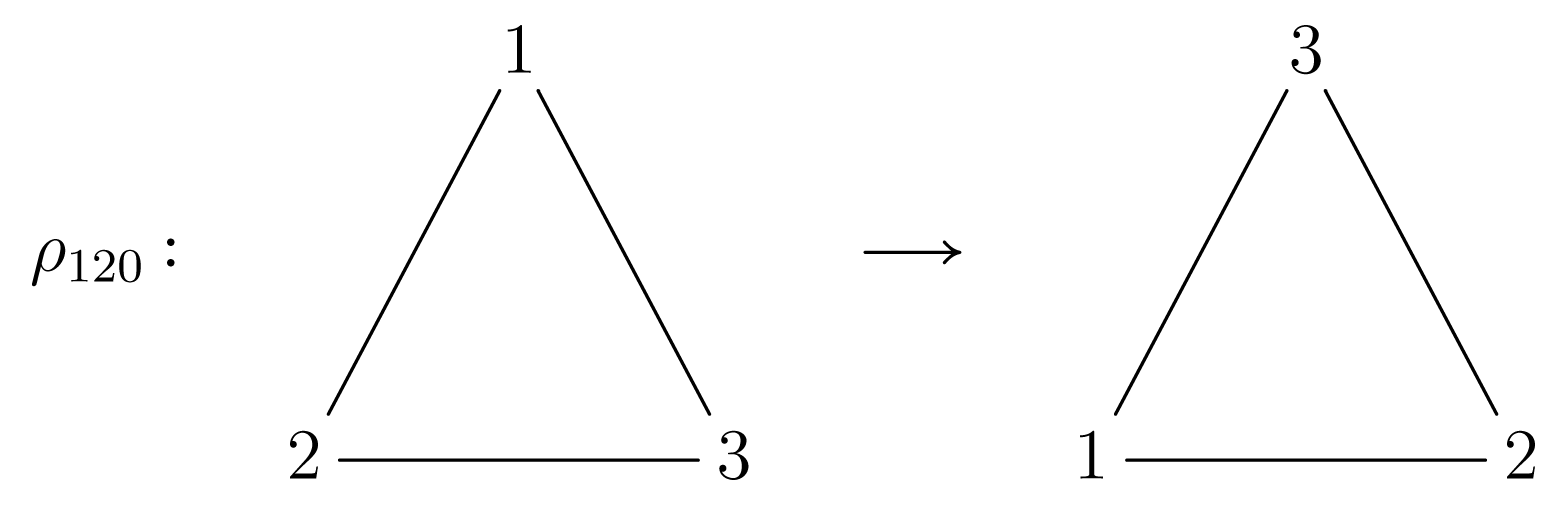 Σχήμα 1.2
Σχήμα 1.2τη μεταβολή του τριγώνου από τη στροφή . Όμοια
| (1.37) |
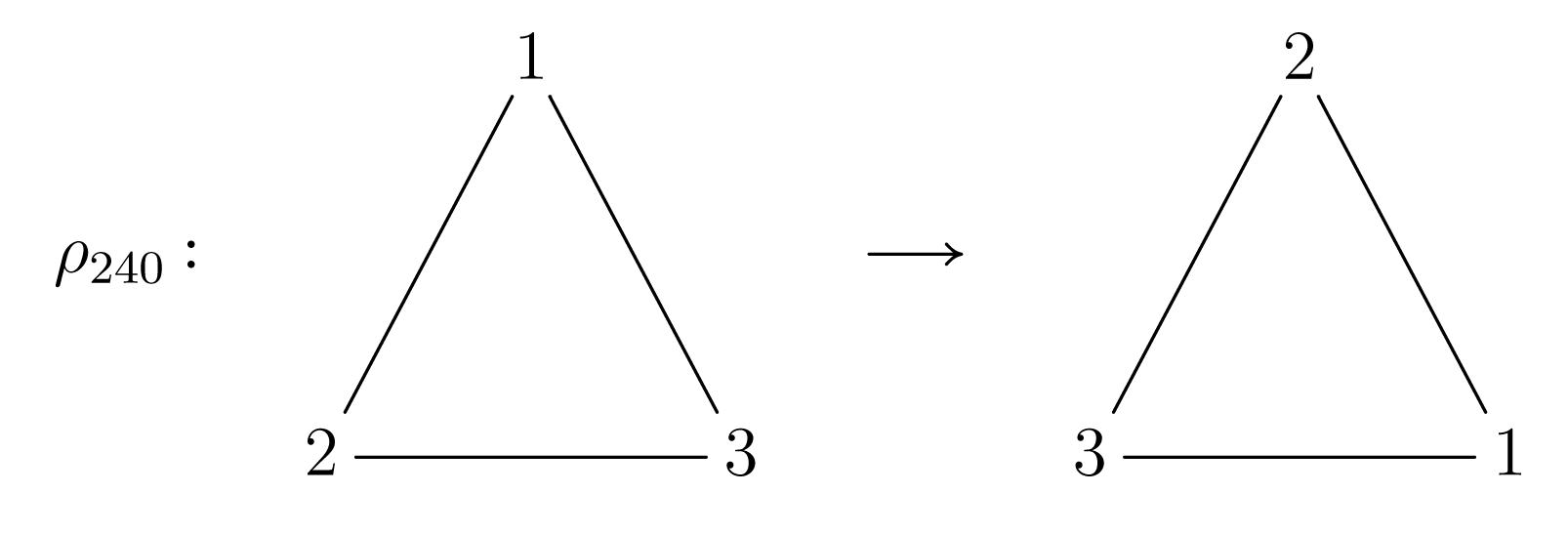
ενώ
| (1.38) |
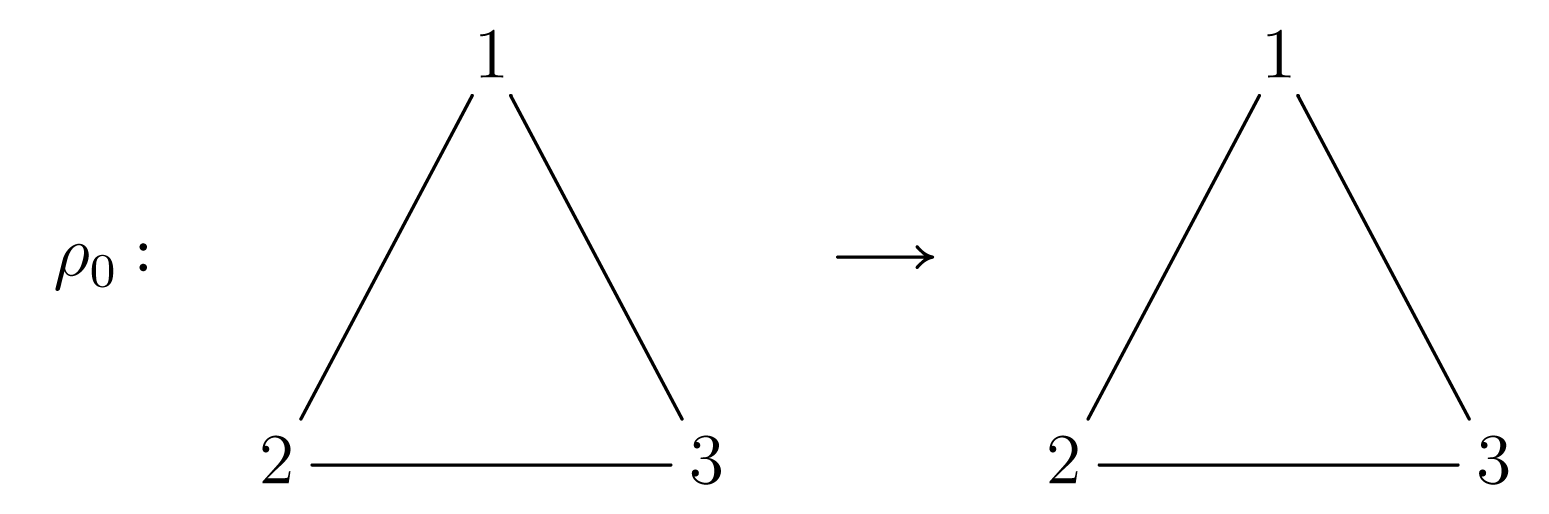 Σχήμα 1.3
Σχήμα 1.3Παρατηρούμε ότι , με , και
| (1.39) |
Μπορούμε εύκολα να διαπιστώσουμε ότι το σύνολο με πράξη τη σύνθεση συναρτήσεων αποτελεί ομάδα.
Ας συμβολίσουμε τώρα με τη στροφή του τριγώνου κατά ως προς άξονα τη μεσοκάθετο του τριγώνου που διέρχεται από την κορυφή . Τότε η είναι επίσης μία αμφιμονότιμη και επί συνάρτηση του συνόλου επί του και
| (1.40) |
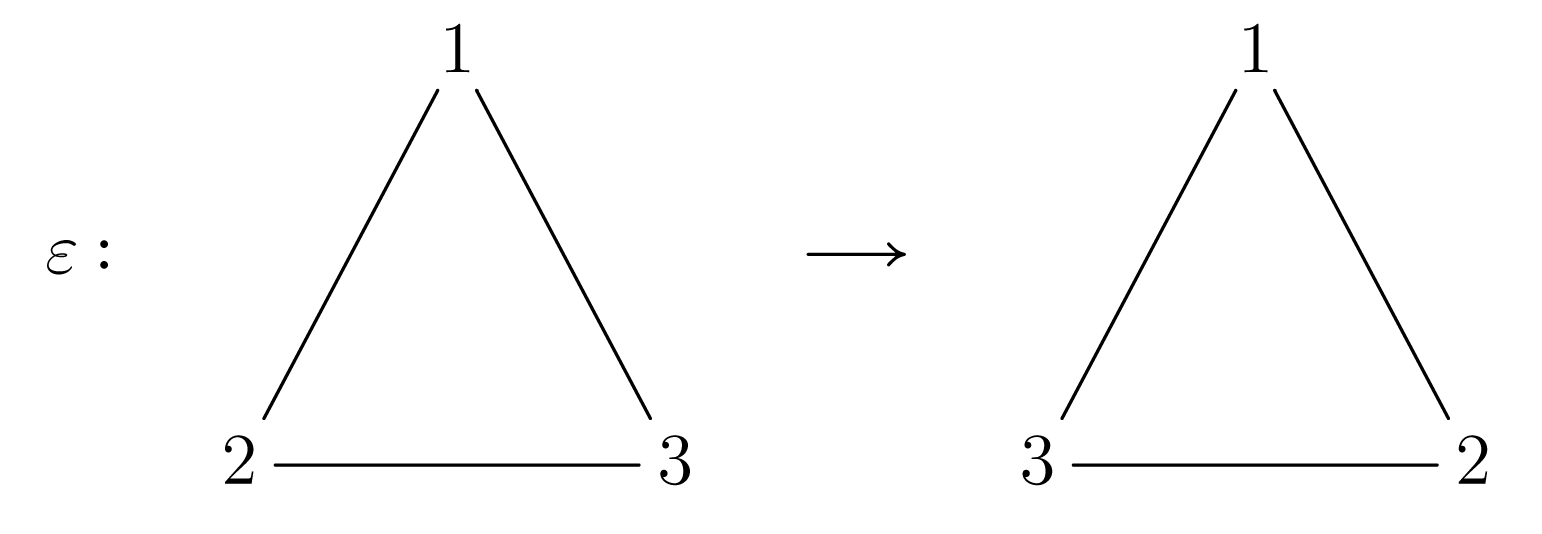 Σχήμα 1.4
Σχήμα 1.4Τώρα παρατηρούμε ότι οι παρακάτω συναρτήσεις είναι επίσης αμφιμονότιμες και επί:
| (1.41) |
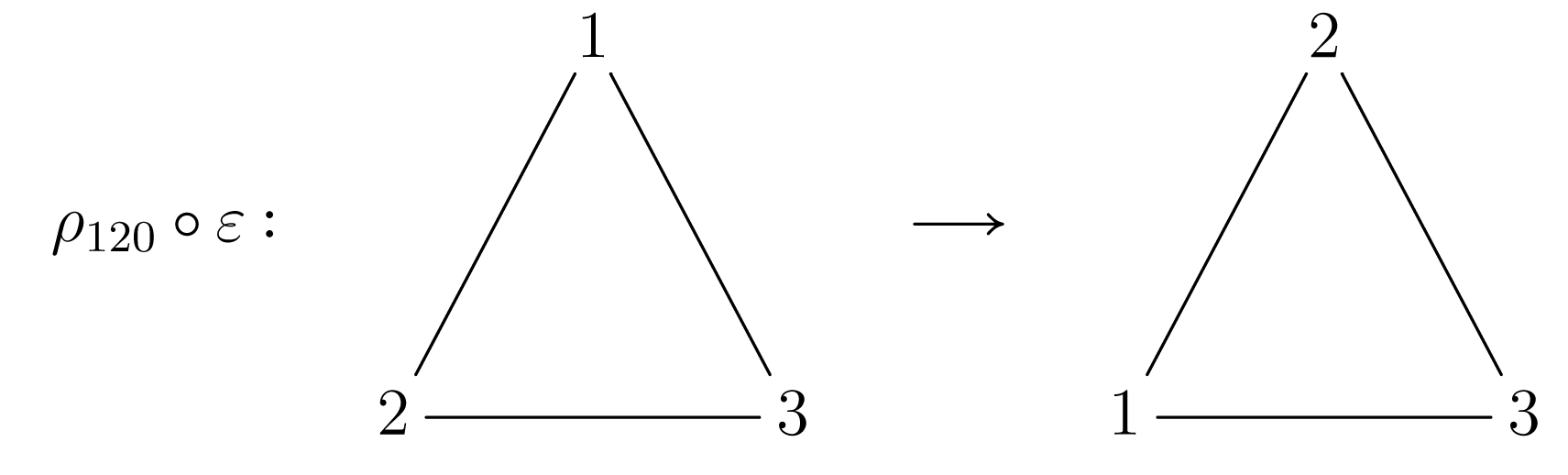 Σχήμα 1.5
Σχήμα 1.5| (1.42) |
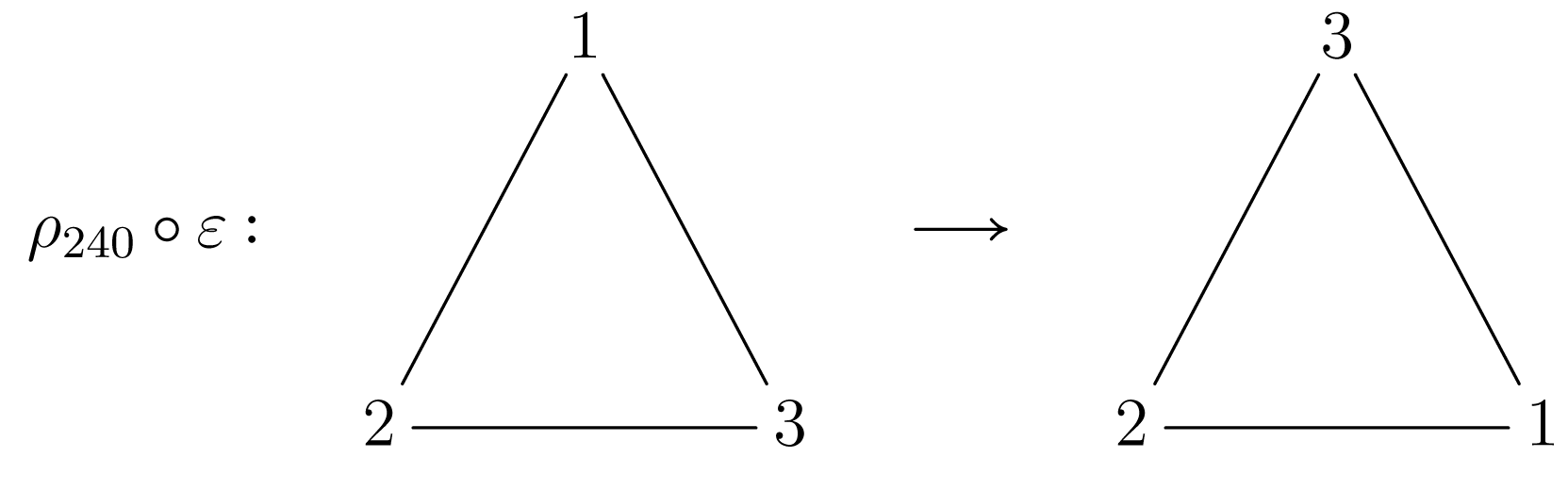 Σχήμα 1.6
Σχήμα 1.6Ακόμη, βλέπουμε αμέσως ότι ισχύουν οι σχέσεις:
| (1.43) |
Ας συμβολίσουμε , , και
| (1.44) |
Η σύνθεση συναρτήσεων βέβαια ορίζεται στο σύνολο , άρα μπορούμε να δημιουργήσουμε τον Πίνακα 1.6 που είναι ο πίνακας Cayley της
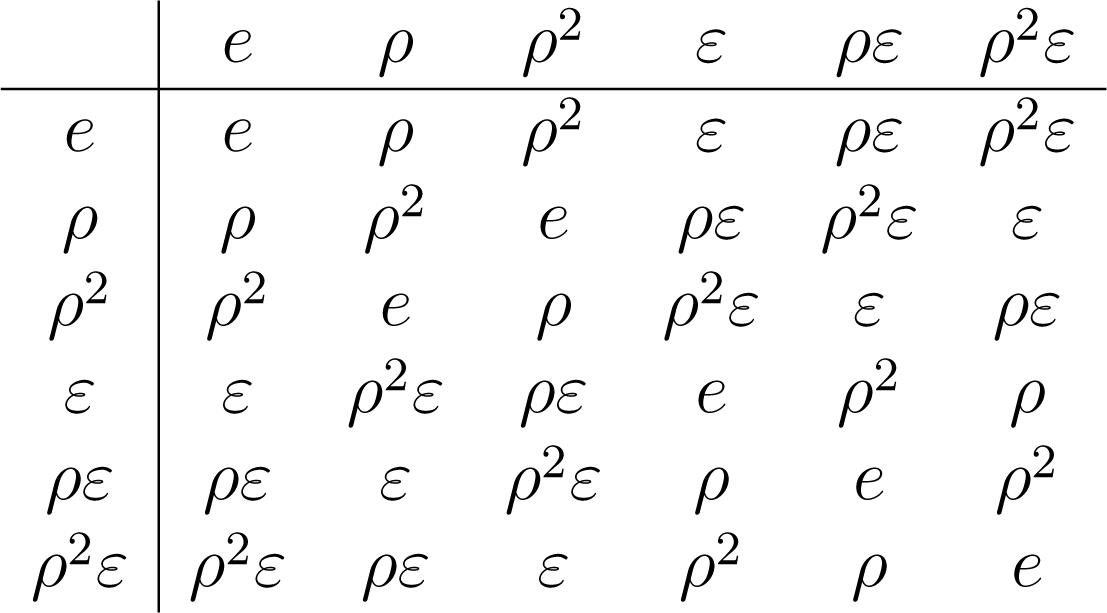 Πίνακας 1.6 |
(1.45) |
και να διαπιστώσουμε ότι η είναι μία μη αβελιανή ομάδα.
Τα στοιχεία της ομάδας ονομάζονται συμμετρίες του ισόπλευρου τριγώνου. Η γραμμική άλγεβρα μας βεβαιώνει ότι αυτές είναι όλες οι συμμετρίες του ισόπλευρου τριγώνου, αλλά η απόδειξη δε θα μας απασχολήσει τώρα. Αργότερα, όμως, θα δώσουμε περισσότερες πληροφορίες.
Ας θεωρήσουμε ως το σύνολο των σημείων ενός τετραγώνου με κορυφές , , , και κέντρο Ο όπως στο Σχήμα 1.7:
| (1.46) |
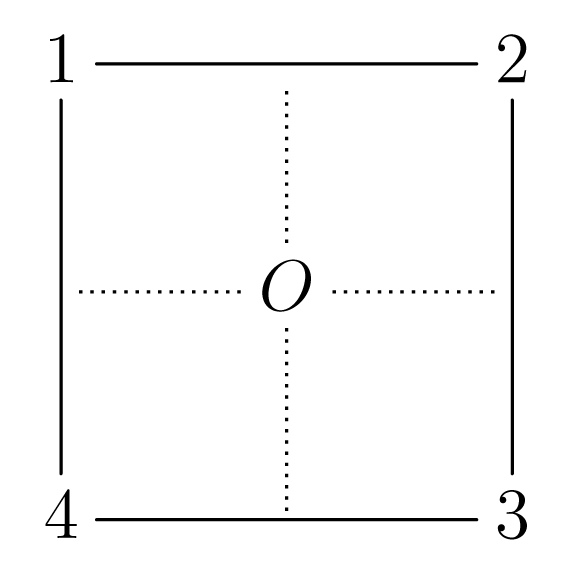 Σχήμα 1.7
Σχήμα 1.7Ας συμβολίσουμε με τη στροφή του τετραγώνου κατά ως προς το κέντρο Ο με φορά αντίστροφη των δεικτών του ρολογιού, με , , . Ακόμη, έστω η στροφή κατά του τετραγώνου ως προς άξονα την ευθεία που διέρχεται από το μέσον της πλευράς των σημείων 1,4 και το κέντρο Ο. Όπως πριν ας συμβολίσουμε
| (1.47) |
Η αλγεβρική δομή είναι επίσης μία μη αβελιανή ομάδα, η οποία λέγεται ομάδα συμμετρίας του τετραγώνου. Έχει στοιχεία και γεωμετρικά, όπως πριν, μπορούμε να διαπιστώσουμε τις σχέσεις:
| (1.48) |
| (1.49) |
Ο πίνακας Cayley της είναι ο Πίνακας 1.7
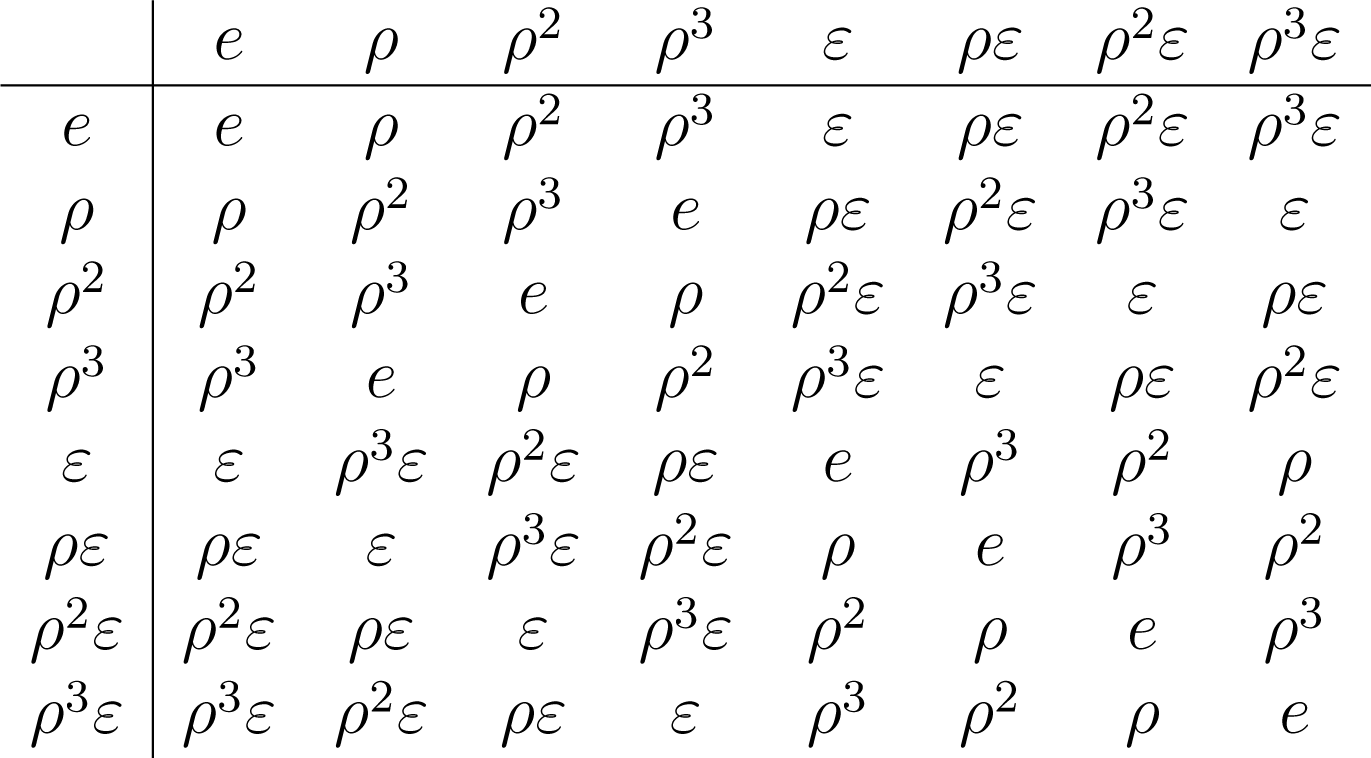 Πίνακας 1.7 |
(1.50) |
Ας παρατηρήσουμε από τον παραπάνω πίνακα ότι η είναι επίσης ομάδα.
Για την οικονομία των εκφράσεων θα δώσουμε τους ακόλουθους ορισμούς.
Ορισμός 1.1.5
Μία αλγεβρική δομή , όπου είναι ένα μη κενό σύνολο, λέγεται ημιομάδα (semigroup) αν η πράξη είναι προσεταιριστική. Η λέγεται μονοειδές (monoid) αν είναι ημιομάδα και έχει ουδέτερο στοιχείο.
Έτσι οι αλγεβρικές δομές
| (1.51) |
είναι μονοειδή, αλλά όχι ομάδες.
Μία ομάδα είναι ένα μονοειδές που κάθε στοιχείο του έχει αντίστροφο στοιχείο.
Ο επόμενος ορισμός χαρακτηρίζει τις ομάδες ανάλογα με το πλήθος των στοιχείων του συνόλου τους.
Ορισμός 1.1.6
Η ομάδα λέγεται πεπερασμένη (finite) αν το σύνολο είναι πεπερασμένο, διαφορετικά λέγεται άπειρη (infinite). Το πλήθος των στοιχείων του συνόλου λέγεται τάξη (order) της ομάδας G.
Έτσι αν , τότε η είναι πεπερασμένη. Ενώ αν , τότε η είναι άπειρη. Η ομάδα έχει τάξη , ενώ η ομάδα είναι άπειρη. Άπειρες είναι επίσης οι ομάδες , , , , , .
Παρατήρηση
Έχουμε διαπιστώσει μέχρι τώρα ότι η ομάδα είναι μία δυάδα που αποτελείται από ένα σύνολο και μία πράξη. Στο ίδιο σύνολο μπορούν να οριστούν περισσότερες από μία πράξεις και διαφορετικές πράξεις στο ίδιο σύνολο δίνουν διαφορετικές αλγεβρικές δομές. Μία ακόμη σημαντική διαπίστωση είναι ότι στον ορισμό της ομάδας δεν μας ενδιαφέρει η φύση των στοιχείων, π.χ. δε μας ενδιαφέρει αν είναι αριθμοί, ή πίνακες, ή συναρτήσεις, ή κλάσεις ισοδυναμίας, ή στροφές, ή συμμετρίες γεωμετρικών σχημάτων. Η φύση των στοιχείων μας ενδιαφέρει αν έχουμε να εξετάσουμε μία συγκεκριμένη ομάδα π.χ. την ομάδα ή την κ.ο.κ.
Επίσης διαπιστώνουμε ότι για τον ορισμό της ομάδας και τη μελέτη των βασικών ιδιοτήτων της, η αριθμητική στο σύνολο ή στο ή στο είναι ένα κίνητρο που επηρεάζει και τις ιδέες μας αλλά και τους συμβολισμούς μας.
Λαμβάνοντας όλα αυτά υπόψη και προκειμένου να έχουμε κατά το δυνατόν απλούστερους συμβολισμούς, στο εξής μία ομάδα θα τη συμβολίζουμε με ένα κεφαλαίο γράμμα του συνόλου της π.χ. ή κ.λ.π.. Πράξη της ομάδας θα εννοείται ο πολλαπλασιασμός και δε θα συμβολίζεται, έτσι θα γράφουμε και όχι για την ομάδα, εκτός αν θέλουμε να δώσουμε έμφαση στην πράξη. Με συμβολίζουμε το ουδέτερο στοιχείο της .
Ασκήσεις
1. Να υπολογίσετε το αντίστροφο του στοιχείου
| (1.52) |
της .
2. Να υπολογίσετε τον πίνακα Cayley των ομάδων , .
3. Να αποδείξετε ότι η ομάδα είναι αβελιανή αν και μόνον αν .
4. Να αποδείξετε ότι το σύνολο
| (1.53) |
με πράξη τον πολλαπλασιασμό πινάκων αποτελεί ομάδα. Η ομάδα λέγεται ειδική γραμμική ομάδα (special linear group) των -πινάκων με στοιχεία από το . (Ανάλογα ορίζονται οι ομάδες
| (1.54) |
5. Να αποδείξετε ότι
-
,
-
.
6. Δίνεται το σύνολο των συναρτήσεων ενός συνόλου που ορίζονται ως εξής: , , , , , , . Να αποδείξετε ότι το σύνολο είναι ομάδα με πράξη τη σύνθεση συναρτήσεων. Να σχηματίσετε τον πίνακα Cayley της . Είναι η αβελιανή;
7. Αν είναι ο μιγαδικός αριθμός που ορίζεται από τη σχέση , να αποδείξετε ότι το σύνολο
| (1.55) |
αποτελεί ομάδα με πράξη τον πολλαπλασιασμό πινάκων. Να σχηματίσετε τον πίνακα Cayley της .
8. Να αποδείξετε ότι δεν είναι πεπερασμένες οι ομάδες , .
9. Έστω το ευθύ εξωτερικό γινόμενο των ομάδων όπου φυσικός αριθμός.
-
i.
Να αποδείξετε ότι η είναι αβελιανή αν και μόνον αν η είναι αβελιανή, για
-
ii.
Αν τότε
-
iii.
Η είναι άπειρη αν μία τουλάχιστον από τις ομάδες είναι άπειρη.
1.2 Βασικές ιδιότητες της έννοιας της Ομάδας
Στην παράγραφο αυτή θα εξετάσουμε ισοδύναμους ορισμούς της ομάδας και βασικές ιδιότητες της ομάδας.
Θεώρημα 1.2.1
Έστω ένα μη κενό σύνολο και μία πράξη στο . Η είναι ομάδα αν και μόνον αν:
-
i.
Η είναι προσεταιριστική.
-
ii.
Υπάρχει ένα στοιχείο τέτοιο ώστε
(1.56) για κάθε στοιχείο .
-
iii.
Για κάθε στοιχείο , υπάρχει ένα στοιχείο τέτοιο ώστε
(1.57)
Απόδειξη: Αν η είναι ομάδα, τότε από τον Ορισμό 1.1.1 προκύπτουν αμέσως τα , , του Θεωρήματος.
Αντίστροφα, έστω ότι ισχύουν τα , , . Πρέπει να αποδείξουμε ότι, για κάθε , ισχύουν οι
| (1.58) |
Από το , για κάθε στοιχείο έχουμε
| (1.59) |
Επομένως
| (1.2.1) |
δηλαδή αποδείχθηκε το του Ορισμού 1.1.1. Χρησιμοποιώντας τη σχέση (1.2.1), έχουμε
| (1.61) |
δηλαδή
| (1.2.2) |
για κάθε . Τώρα από το και τη σχέση (1.2.2) προκύπτει ότι, για κάθε ,
| (1.63) |
δηλαδή το του Ορισμού 1.1.1 και ολοκληρώθηκε η απόδειξη.
Ανάλογα με το Θεώρημα 1.2.1 μπορούμε να αποδείξουμε τον επόμενο ισοδύναμο ορισμό της έννοιας της ομάδας.
Θεώρημα 1.2.2
Έστω ένα μη κενό σύνολο και μία πράξη στο . Η είναι ομάδα αν και μόνον αν:
-
i.
Η είναι προσεταιριστική.
-
ii.
Υπάρχει ένα στοιχείο τέτοιο ώστε
(1.64) για κάθε στοιχείο .
-
iii.
Για κάθε στοιχείο , υπάρχει ένα στοιχείο τέτοιο ώστε
(1.65)
Το στοιχείο της που ικανοποιεί το του Θεωρήματος 1.2.1 λέγεται αριστερό ουδέτερο στοιχείο (left unit element) της , ενώ το στοιχείο που ικανοποιεί το του ίδιου Θεωρήματος λέγεται αριστερό αντίστροφο (left inverse) του στοιχείου .
Έτσι ο ισχυρισμός του Θεωρήματος 1.2.1 είναι ότι μία ημιομάδα είναι ομάδα αν και μόνον αν υπάρχει αριστερό ουδέτερο στοιχείο στο και κάθε στοιχείο έχει αριστερό αντίστροφο.
Ανάλογα ένα στοιχείο της ημιομάδας λέγεται δεξιό ουδέτερο στοιχείο (right unit) της αν ικανοποιείται το του Θεωρήματος 1.2.2. Ενώ το στοιχείο που ικανοποιεί το του Θεωρήματος 1.2.2 λέγεται δεξιό αντίστροφο (right inverse) του στοιχείου .
Έτσι ο ισχυρισμός του Θεωρήματος 1.2.2 είναι, ότι μία ημιομάδα είναι ομάδα αν και μόνον αν υπάρχει δεξιό ουδέτερο στοιχείο στο και κάθε στοιχείο του έχει δεξιό αντίστροφο στοιχείο στο .
Συνεχίζουμε με την εξέταση βασικών ιδιοτήτων των ομάδων και με έναν ακόμα ισοδύναμο ορισμό της έννοιας της ομάδας.
Πρόταση 1.2.3
Σε κάθε ομάδα ισχύει η απλοποίηση και από αριστερά και από δεξιά, δηλαδή ισχύουν οι επόμενες προτάσεις:
-
i.
Αν , για , τότε
-
ii.
Αν , για , τότε
Απόδειξη: Έστω στοιχεία στοιχεία της ομάδας , από τη σχέση
| (1.66) |
. Όμοια αποδεικνύεται η .
Έτσι παρατηρούμε ότι η απλοποίηση επιτρέπεται στις ομάδες , , . Όμως στην αλγεβρική δομή δεν επιτρέπεται η απλοποίηση αφού από τη σχέση
| (1.67) |
Πρόταση 1.2.4
Έστω μία ομάδα.
-
i.
Για κάθε στοιχείο ισχύει
(1.68) -
ii.
Αν είναι τυχαία στοιχεία του , τότε
(1.69)
Απόδειξη: Έστω . Από τη σχέση
| (1.70) |
προκύπτει, αφού το αντίστροφο στοιχείο ορίζεται μοναδικά, ότι το είναι το αντίστροφο του στοιχείου . Άρα
| (1.71) |
Επειδή ισχύει ο γενικευμένος προσεταιριστικός νόμος (βλ. Παράρτημα A) το στοιχείο ορίζεται μοναδικά στο σύνολο χωρίς να υπάρχουν παρενθέσεις, για . Παρατηρούμε ότι
| (1.72) |
Επομένως
| (1.73) |
Άρα ολοκληρώθηκε η απόδειξη.
Πρόταση 1.2.5
Έστω μία ομάδα.
-
i.
Η αντιστοιχία
(1.74) είναι αμφιμονότιμη και επί.
-
ii.
Έστω ένα στοιχείο της , τότε οι αντιστοιχίες
(1.75) είναι αμφιμονότιμες και επί συναρτήσεις.
Απόδειξη: . Η είναι αμφιμονότιμη συνάρτηση, γιατί αν , τότε
| (1.76) |
Η είναι επί συνάρτηση γιατί, αν είναι τυχαίο στοιχείο της , τότε και σύμφωνα με την Πρόταση 1.2.4
| (1.77) |
Άρα η είναι αμφιμονότιμη και επί συνάρτηση.
. Η είναι αμφιμονότιμη συνάρτηση γιατί από τον ορισμό της πράξης και την Πρόταση 1.2.3 έχουμε, για
| (1.78) |
Η είναι επί συνάρτηση γιατί αν , τότε υπάρχει το στοιχείο ώστε . Άρα η είναι αμφιμονότιμη και επί συνάρτηση. Όμοια αποδεικνύεται ότι η είναι επίσης αμφιμονότιμη και επί συνάρτηση.
Παρατήρηση: Η Πρόταση 1.2.5, ουσιαστικά μας λέει ότι όταν ένα στοιχείο της ομάδας διατρέχει όλα τα στοιχεία της , τότε και το αντίστροφο του διατρέχει όλα τα στοιχεία της .
Το της Πρότασης 1.2.5 μας προσφέρει μία ενδιαφέρουσα πληροφορία για τον πίνακα Cayley μίας ομάδας . Μία γραμμή αυτού του πίνακα, έστω αυτή που το αριστερό στοιχείο της είναι το , έχει ως στοιχεία τα , όπου το διατρέχει όλα τα στοιχεία της . Αυτά τα στοιχεία είναι διακεκριμένα και ακριβώς όλα τα στοιχεία της , σύμφωνα με τις ιδιότητες της συνάρτησης της Πρότασης 1.2.5. Έτσι κάθε γραμμή του πίνακα Cayley της περιέχει ακριβώς όλα τα στοιχεία του . Ανάλογο συμπέρασμα ισχύει για τις στήλες του πίνακα Cayley της : Κάθε στήλη περιέχει ακριβώς όλα τα στοιχεία του .
Παραδείγματα 1.2.6
Υπάρχει ομάδα με ένα μόνον στοιχείο; Μία τέτοια ομάδα έχει σύνολο το και πίνακα Cayley τον
Πίνακας 1.8
Βέβαια δεν υπάρχει ομάδα με σύνολο το .
Μπορούμε να κατασκευάσουμε μία ομάδα με δύο στοιχεία, έστω ; Αν υπάρχει μία τέτοια ομάδα θα έχει πίνακα Cayley τον ακόλουθο:
Πίνακας 1.9
δηλαδή αναγκαστικά , ισοδύναμα . Κατασκευάσαμε επομένως μία ομάδα με δύο στοιχεία. Παρατηρούμε ότι η είναι μία ομάδα με δύο στοιχεία (βλ. Παράδειγμα 1.1.2.9).
Με την παραπάνω διαδικασία μπορούμε να κατασκευάσουμε μία ομάδα με τρία στοιχεία. Πράγματι, έστω το σύνολο της ομάδας με τρία στοιχεία, με το ουδέτερο στοιχείο της. Ο πίνακας Cayley της σύμφωνα με το περιεχόμενο της παραπάνω Παρατήρησης πρέπει να είναι ο ακόλουθος
Πίνακας 1.10
διότι σε κάθε γραμμή και σε κάθε στήλη του πίνακα πρέπει να υπάρχουν όλα τα στοιχεία του . Επομένως για μία τέτοια ομάδα έχουμε τις σχέσεις
| (1.79) |
δηλαδή .
Στο σύνολο ορίζουμε μία πράξη όπως περιγράφεται στον ακόλουθο πίνακα Cayley
Πίνακας 1.11
Είναι φανερό ότι το είναι το ουδέτερο στοιχείο της . Η πράξη είναι αντιμεταθετική, αφού ο πίνακας Cayley είναι συμμετρικός. Παρατηρούμε ότι , , . Τέλος εύκολα, αλλά με δουλειά ρουτίνας, μπορούμε να διαπιστώσουμε ότι η πράξη είναι προσεταιριστική. Άρα η είναι μία αβελιανή ομάδα τάξης .
Θεωρούμε το σύνολο
| (1.80) |
Παρατηρούμε ότι ο πολλαπλασιασμός - πινάκων ορίζεται στο , αφού για
| (1.81) |
Έτσι η είναι αλγεβρική δομή. Ο πολλαπλασιασμός πινάκων όταν ορίζεται είναι προσεταιριστική πράξη. Άρα η πράξη αυτή στο είναι προσεταιριστική. Είναι φανερό ότι η πράξη είναι αντιμεταθετική στο . Ακόμη βλέπουμε ότι
| (1.82) |
και
| (1.83) |
δηλαδή το είναι το αριστερό μοναδιαίο στοιχείο και το τυχαίο στοιχείο έχει αριστερό αντίστροφο το . Επομένως η είναι αβελιανή ομάδα. Τέλος , δηλαδή η είναι άπειρη ομάδα.
Θεώρημα 1.2.7
Η αλγεβρική δομή είναι ομάδα αν και μόνον αν
-
i.
Η είναι προσεταιριστική, δηλαδή η είναι ημιομάδα.
-
ii.
Κάθε μία από τις εξισώσεις
(1.84) για όλα τα , έχει λύση στο σύνολο .
Απόδειξη: Ας υποθέσουμε ότι η είναι ομάδα, φυσικά η ισχύει από τον ορισμό της ομάδας. Για την απόδειξη του παρατηρούμε ότι για
| (1.85) |
δηλαδή η εξίσωση έχει λύση στο σύνολο το , η οποία είναι μοναδική αφού η είναι συνάρτηση. Όμοια η έχει, επίσης μοναδική, λύση στο την .
Αντίστροφα τώρα υποθέτουμε ότι ισχύουν τα και . Θα αποδείξουμε τα και του Θεωρήματος 1.2.1. Υποθέτουμε ότι οι εξισώσεις
| (1.86) |
έχουν λύση στο , για όλα τα . Η εξίσωση για , βεβαιώνει ότι υπάρχει στοιχείο , ώστε . Θα αποδείξουμε ότι το είναι αριστερό ουδέτερο στοιχείο της , δηλαδή , . Η εξίσωση έχει λύση στο , έστω την , για το τυχαίο . Δηλαδή για . Επομένως, για κάθε έχουμε
| (1.87) |
Με άλλα λόγια το είναι αριστερό ουδέτερο στοιχείο της , αυτό αποδεικνύει το του Θεωρήματος 1.2.1.
Τέλος, για το τυχαίο στοιχείο , υπάρχει ένα στοιχείο που είναι λύση της εξίσωσης . Αυτό σημαίνει ότι το είναι το αριστερό συμμετρικό στοιχείο του στην , αυτό αποδεικνύει το του Θεωρήματος 1.2.1. Άρα η είναι ομάδα.
Παρατήρηση: Από την Πρόταση 1.2.5 και την Παρατήρηση που την ακολουθεί, είδαμε ότι σε κάθε γραμμή και σε κάθε στήλη του πίνακα Cayley μίας ομάδας υπάρχουν ακριβώς όλα τα στοιχεία της ομάδας. Το Θεώρημα 1.2.7 απαντά καταφατικά στο ερώτημα: Αν έχουμε τον πίνακα Cayley μίας ημιομάδας, δηλαδή η πράξη είναι προσεταιριστική, και σε κάθε γραμμή και σε κάθε στήλη του πίνακα βρίσκονται όλα τα στοιχεία του συνόλου της ημιομάδας, τότε συμπεραίνουμε ότι η αλγεβρική δομή είναι ομάδα;
Η απάντηση είναι ναι, γιατί οι λύσεις είναι τα στοιχεία της γραμμής του πίνακα που ξεκινάει από το και οι λύσεις της είναι τα στοιχεία της στήλης του πίνακα που ξεκινάει από το .
Ο αναγνώστης μπορεί να συμπεράνει ότι κάθε πίνακας Sudoku δεν είναι πίνακας Cayley μίας ομάδας, κάποιοι από αυτούς είναι.
Παραδείγματα 1.2.8
Μπορούμε να υπολογίσουμε τον πίνακα Cayley μίας ομάδας τάξης ; Ας εξετάσουμε το ερώτημα. Ήδη το Παράδειγμα της σελίδας 1.2.6 δίνει έναν πίνακα Cayley μίας ομάδας τάξης . Όπως διαπιστώσαμε η ομάδα προσδιορίζεται από το σύνολο και την πράξη που ορίζεται σε αυτό. Μήπως σε ένα σύνολο με στοιχεία μπορούμε να ορίσουμε και μία άλλη πράξη ώστε αυτό να αποτελεί επίσης ομάδα;
Λοιπόν, ας θεωρήσουμε μία ομάδα με σύνολο και την πράξη που ορίζεται σε αυτό ας την ονομάσουμε πολλαπλασιασμό και ας τη συμβολίσουμε με , έτσι αν , είναι το γινόμενο των στοιχείων αυτών στο . Με συμβολίζουμε το μοναδιαίο στοιχείο της . Το στοιχείο δεν μπορεί να είναι το (βλέπε Πρόταση 1.2.5 και την Παρατήρηση που την ακολουθεί). Επομένως το μπορεί να είναι ένα από τα στοιχεία . ας υποθέσουμε ότι . Τότε το δεν μπορεί να είναι κανένα από τα στοιχεία και . Άρα η μόνη δυνατή τιμή για το είναι το και τότε . Το στοιχείο δεν μπορεί να είναι κανένα από τα και . Άρα . Τότε, όμως, το στοιχείο μπορεί να πάρει μόνον την τιμή . Το στοιχείο μπορεί να λάβει την τιμή ή την τιμή . Αν , τότε , , . Αν , τότε , , . Έτσι αν , οδηγούμαστε στους Πίνακες 1.12 και 1.13
 Πίνακας 1.12 |
 Πίνακας 1.13 |
(1.88) |
Ας υποθέσουμε τώρα ότι , τότε καταλήγουμε στον Πίνακα 1.14 και αν , τότε καταλήγουμε στον Πίνακα 1.15.
 Πίνακας 1.14 |
 Πίνακας 1.15 |
(1.89) |
Έτσι μπορούμε να ορίσουμε τέσσερις πράξεις στο σύνολο ώστε να αποτελεί ομάδα. Θα δούμε αργότερα πόσο διαφορετικές είναι αυτές οι ομάδες με πίνακα Cayley τους εμφανιζόμενους παραπάνω. Βέβαια από την διαδικασία που ακολουθήσαμε η φύση των στοιχείων του συνόλου δεν παίζει ουσιαστικό ρόλο.
Από τους Πίνακες 1.12 - 1.15 παρατηρούμε ότι οι εμφανιζόμενες ομάδες είναι αβελιανές. Έτσι συμπαιρένουμε ότι κάθε ομάδα τάξης είναι αβελιανή. Όμως μπορούμε να οδηγηθούμε στο συμπέρασμα αυτό χωρίς τον υπολογισμό των πινάκων 1.12 - 1.15, όπως θα δούμε στο επόμενο παράδειγμα.
Κάθε ομάδα τάξης είναι αβελιανή. Πράγματι: έστω μία ομάδα τάξης . Τότε το στοιχείο μπορεί να λάβει μόνον τις τιμές ή (αν π.χ. , τότε ). Αν , τότε , από τον ορισμό της ομάδας. Άρα . Έστω . Τότε το μπορεί επίσης να λάβει την τιμή ή . Αν , τότε . Αυτό, όμως, είναι αδύνατον αφού . Επομένως η μόνη δυνατή περίπτωση είναι , οπότε . Με τον ίδιο τρόπο συμπαιρένουμε ότι και . Άρα η είναι αβελιανή.
Έστω μία ομάδα τάξης της οποίας δίνεται στον Πίνακα 1.16 τμήμα του πίνακα Cayley.
 Πίνακας 1.16 |
(1.90) |
Μπορούμε να τον συμπληρώσουμε; Η απάντηση είναι ναι. Ας το επιχειρήσουμε. Το στοιχείο οφείλει να είναι το , ώστε στη δεύτερη γραμμή να είναι όλα τα στοιχεία της . Το στοιχείο μπορεί να είναι μόνον το , αφού δεν μπορεί να είναι κανένα από τα που βρίσκονται ήδη στην τρίτη στήλη, ούτε το που βρίσκεται στην τέταρτη γραμμή. Επομένως το στοιχείο πρέπει να είναι το , το στοιχείο πρέπει να είναι το και το στοιχείο πρέπει να είναι το . Το στοιχείο έχει τη δυνατότητα να είναι το ή το . Αν είναι το , τότε το στοιχείο πρέπει να είναι το . Αυτό, όμως, είναι αδύνατον γιατί υπάρχει το στην τέταρτη στήλη. Επομένως και . Τέλος είναι φανερό ότι και . Έτσι ο πίνακας Cayley της δοθείσας ομάδας είναι ο Πίνακας 1.17
 Πίνακας 1.17 |
(1.91) |
Από τον Πίνακα 1.17 προκύπτει αμέσως ότι η είναι αβελιανή.
Το επόμενο συμπέρασμα μας προσφέρει μία άλλη εφαρμογή του Θεωρήματος 1.2.7. Η αποδεικτική μέθοδος που θα ακολουθήσουμε χρησιμοποιείται συχνά προκειμένου να διαπιστώσουμε αν μία ημιομάδα είναι ομάδα.
Πρόταση 1.2.9
Έστω μία ημιομάδα και , για . Αν η απλοποίηση στο σύνολο επιτρέπεται από αριστερά και δεξιά τότε η είναι ομάδα.
Απόδειξη: Έστω μία ημιομάδα με . Σχηματίζουμε τα στοιχεία . Τα στοιχεία αυτά ανήκουν προφανώς στο σύνολο και επιπλέον είναι διακεκριμένα, εφόσον επιτρέπεται η απλοποίηση στην από αριστερά. Πράγματι, αν για , , ισχύει
| (1.92) |
Με άλλα λόγια
| (1.93) |
δηλαδή, για το στοιχείο , υπάρχει ένα στοιχείο ώστε . Αυτό σημαίνει ότι η εξίσωση , , έχει λύση στην .
Όμοια εφόσον επιτρέπεται η απλοποίηση στην από δεξιά, καταλήγουμε στο συμπέρασμα ότι η εξίσωση , , έχει λύση στην .
Τώρα ο ισχυρισμός της Πρότασης προκύπτει αμέσως από το Θεώρημα 1.2.7, αφού η πράξη είναι προσεταιριστική.
Θα πρέπει να παρατηρήσουμε ότι η Πρόταση 1.2.9 δεν ισχύει όταν το σύνολο δεν είναι πεπερασμένο. Για παράδειγμα το σύνολο , όπου , εφοδιασμένο με την πράξη του πολλαπλασιασμού είναι μία αβελιανή ημιομάδα, που επιτρέπεται η απλοποίηση από αριστερά και συνεπώς από δεξιά. Πράγματι, αν , τότε από τις ιδιότητες των ακεραίων ισχύει
| (1.94) |
Όμως η δεν είναι ομάδα γιατί δεν υπάρχει μοναδιαίο στοιχείο και βέβαια κάθε στοιχείο του δεν έχει αντίστροφο.
Ασκήσεις
1. Να αποδείξετε ότι σε μία ομάδα οι εξισώσεις και , για , έχουν μοναδική λύση στο .
2. Να συμπληρώσετε τον Πίνακα 1.18 ώστε να βρείτε τον πίνακα Cayley της ομάδας , για ,
 Πίνακας 1.18 |
(1.95) |
1.3 Δυνάμεις στοιχείων ομάδας
Από τον γενικευμένο προσεταιριστικό νόμο προκύπτει ότι σε μία ομάδα ορίζεται το στοιχείο , για τυχαίο φυσικό αριθμό και για οποιαδήποτε στοιχεία . Η θέση των παρενθέσεων δεν έχει σημασία εξαιτίας του γενικευμένου προσεταιριστικού νόμου και για αυτόν τον λόγο παραλείπονται. Βεβαίως η σειρά των στοιχείων σε αυτή την παράσταση είναι απαραίτητη, εφόσον η δεν είναι αβελιανή. Έτσι το στοιχείο ορίζεται μοναδικά στο σύνολο . Αν για κάποιο , τότε το στοιχείο , για πλήθος στοιχεία , συμβολίζεται ως . Ο συμβολισμός αυτός προκύπτει από τον αντίστοιχο συμβολισμό για το γινόμενο αριθμών.
Το στοιχείο λέγεται -οστή δύναμη (power) του στοιχείου , για τον φυσικό αριθμό .
Το αντίστροφο του στοιχείου , δηλαδή το , είναι φανερό ότι είναι το , με πλήθος στοιχεία , αφού
| (1.96) |
Άρα , για . Συμφωνούμε, όπως στο γινόμενο αριθμών, ότι , όπου είναι το ουδέτερο στοιχείο της ομάδας .
Ορίζουμε , για κάθε . Ο ορισμός αυτός μιμείται τον αντίστοιχο των αριθμών. Έτσι οδηγούμαστε στον ακόλουθο ορισμό.
Ορισμός 1.3.1
Έστω και . Ορίζουμε τις δυνάμεις , , ως εξής:
| (1.97) |
Αν η πράξη συμβολίζεται προσθετικά, τότε για τα στοιχεία της ομάδας έχουμε τον συμβολισμό
| (1.98) |
Το επόμενο Θεώρημα συγκεντρώνει τις βασικές ιδιότητες των δυνάμεων στοιχείων μίας ομάδας.
Θεώρημα 1.3.2
Έστω μία ομάδα και . Ισχύουν οι επόμενες προτάσεις:
-
i.
, για κάθε .
-
ii.
, για κάθε .
-
iii.
, για κάθε .
Απόδειξη: Τα , , αποδεικνύονται επαγωγικά ως προς . Οι αποδείξεις αυτές αφήνονται για τον αναγνώστη.
Μένει να αποδείξουμε τις προτάσεις αυτές για αρνητικούς ακέραιους.
Έστω και . Τότε από τον Ορισμό 1.3.1, την , για φυσικό αριθμό , και την Πρόταση 1.2.4 ισχύει
| (1.3.1) |
και ακόμη
| (1.3.2) |
Από τις σχέσεις (1.3.1), (1.3.2) προκύπτει ότι
| (1.101) |
δηλαδή αποδείχθηκε η .
Θα αποδείξουμε την περίπτωση που και . Οι άλλες περιπτώσεις αποδεικνύονται ανάλογα και αφήνονται για τον αναγνώστη. Έστω , για και , τότε
| (1.102) |
Αν , τότε
| (1.103) |
Αν , τότε
| (1.104) |
Αποδείξαμε το .
Αφήνεται ως άσκηση για τον αναγνώστη.
Παραδείγματα 1.3.3
Έστω μία ομάδα και τέτοιο ώστε . Παρατηρούμε ότι
| (1.105) |
Έτσι, ικανή και αναγκαία συνθήκη ώστε ένα στοιχείο της ομάδας να ισούται με το αντίστροφό του, είναι το τετράγωνό του να ισούται με το ουδέτερο στοιχείο της ομάδας.
Θα δούμε αμέσως ότι αν για κάθε στοιχείο του , τότε αναγκαστικά η είναι αβελιανή. Πράγματι, είδαμε ότι . Έστω , τότε
| (1.106) |
δηλαδή , για όλα τα στοιχεία . Άρα η είναι αβελιανή. Καταλήγουμε έτσι στην επόμενη πρόταση
Πρόταση 1.3.4
Έστω μία ομάδα. Τότε:
-
i.
Για ένα , αν και μόνον αν .
-
ii.
Αν , για κάθε , τότε η είναι αβελιανή.
Θα αποδείξουμε ότι αν για όλα τα στοιχεία , μίας ομάδας , τότε η ομάδα είναι αβελιανή. Πράγματι; η σχέση
| (1.107) |
αφού επιτρέπεται η απλοποίηση από αριστερά και από δεξιά σε κάθε ομάδα. Άρα η είναι αβελιανή.
Ασκήσεις
1. Να ολοκληρώσετε την απόδειξη του Θεωρήματος 1.3.2.
2. Δίνονται δύο στοιχεία , μιας ομάδας τέτοια ώστε . Να αποδείξετε ότι και τα στοιχεία , της , για κάθε , επίσης αντιμετατίθενται.
3. Επαγωγικά να αποδείξετε ότι αν είναι στοιχεία μιας ομάδας , τότε
| (1.108) |
4. Έστω μία πεπερασμένη ομάδα και . Να αποδείξετε ότι υπάρχει ένας φυσικός αριθμός τέτοιος ώστε .
5. Αν , είναι στοιχεία μίας ομάδας τέτοια ώστε και , να αποδείξετε ότι και .
6. Δίνονται δύο στοιχεία , μιας ομάδας τέτοια ώστε , όπου είναι ένας σταθερός φυσικός αριθμός διάφορος του μηδενός. Να αποδείξετε επαγωγικά ότι
-
, ,
-
, .
7. Να αποδείξετε ότι αν σε μία ομάδα ισχύει για τρεις διαδοχικούς ακέραιους αριθμούς , τότε η είναι αβελιανή.