Κεφάλαιο 2Υποομάδες και ομομορφισμοί ομάδων
2.1 Υποομάδες
Μεταξύ των παραδειγμάτων των ομάδων που αναφέραμε στην προηγούμενη παράγραφο ήταν και οι , , , . Παρατηρούμε ότι και ότι αν η πρόσθεση στο περιοριστεί στα στοιχεία του δίνει την πρόσθεση στο κ.ο.κ. Η παρατήρηση αυτή δίνει την αφορμή για τον ορισμό της υποομάδας.
Ορισμός 2.1.1
Έστω μία ομάδα. Ένα υποσύνολο λέμε ότι είναι υποομάδα (subgroup) της , αν η πράξη ορίζεται στο και η είναι ομάδα και συμβολίζουμε , ή όταν γνωρίζουμε ότι .
Είναι φανερό ότι και . Η λέγεται τετριμμένη (trivial) υποομάδα της . Κάθε υποομάδα της τέτοια ώστε λέγεται γνήσια (proper) υποομάδα της . Με τον συμβολισμό εννοούμε ότι η είναι γνήσια υποομάδα της .
Πρόταση 2.1.2
Έστω μία ομάδα και . Το ουδέτερο στοιχείο της συμπίπτει με το ουδέτερο στοιχείο της και το αντίστροφο ενός στοιχείου συμπίπτει με το αντίστροφο στοιχείο του , αν αυτό το θεωρήσουμε ως στοιχείο της .
Απόδειξη: Σε κάθε ομάδα το ουδέτερο στοιχείο της είναι το μόνο που ικανοποιεί την εξίσωση . Εφόσον η πράξη της συμπίπτει με την πράξη της έπεται ότι το ουδέτερο στοιχείο της που ικανοποιεί την εξίσωση και στην ομάδα και στην ομάδα , συμπίπτει με το ουδέτερο στοιχείο της .
Εξαιτίας της σύμπτωσης των ουδέτερων στοιχείων της και της προκύπτει ότι το είναι το ίδιο είτε θεωρήσουμε το ως στοιχείο της είτε το θεωρήσουμε ως στοιχείο της .
Πριν προχωρήσουμε σε παραδείγματα υποομάδων αποδεικνύουμε ένα κριτήριο για να είναι υποομάδα ένα υποσύνολο μίας ομάδας. Είναι φανερό ότι ένα υποσύνολο της που δεν περιέχει το ουδέτερο στοιχείο της δεν μπορεί να είναι υποομάδα της .
Θεώρημα (Κριτήριο Υποομάδας) 2.1.3
Έστω μία ομάδα και ένα μη κενό υποσύνολο του . Το αποτελεί υποομάδα της αν και μόνον αν ισχύει:
| 2.1.1 |
Απόδειξη: Από τον ορισμό της ομάδας είναι φανερό ότι αν , τότε ισχύει η συνθήκη του Θεωρήματος.
Ας υποθέσουμε, τώρα, ότι ισχύει η σχέση (2.1.1) για το μη κενό υποσύνολο της . Έστω , τότε από τη σχέση (2.1.1) έπεται ότι , δηλαδή , όπου είναι το ουδέτερο στοιχείο της . Πάλι από τη σχέση (2.1.1), αφού τα , προκύπτει ότι , δηλαδή . Τώρα θα αποδείξουμε ότι η πράξη της ομάδας ορίζεται στο σύνολο . Έστω , τότε το , όπως είδαμε. Άρα από τη σχέση (2.1.1) έχουμε ότι , δηλαδή , για όλα τα στοιχεία . Με άλλα λόγια η πράξη της ορίζεται στο σύνολο . Μένει τώρα να δείξουμε ότι η πράξη στο είναι προσεταιριστική. Αυτό, όμως, συμβαίνει γιατί η πράξη αυτή είναι προσεταιριστική στην , άρα και στο . Αποδείξαμε, επομένως, ότι το είναι υποομάδα της .
Το παραπάνω κριτήριο εφαρμοζόμενο μας επιτρέπει να συμπεράνουμε αν ένα υποσύνολο μίας ομάδας είναι υποομάδα της με πράξεις σαφώς λιγότερες από αυτές που απαιτούνται αν είχαμε να ελέγξουμε όλα τα αξιώματα του ορισμού της ομάδας.
Ιδιαίτερα αν το σύνολο είναι πεπερασμένο, τότε οι απαιτούμενες πράξεις για τον έλεγχο αν το αποτελεί υποομάδα της είναι ακόμη λιγότερες. Αυτό διαβεβαιώνει το επόμενο θεώρημα.
Θεώρημα 2.1.4
Ένα μη κενό πεπερασμένο υποσύνολο μίας ομάδας είναι υποομάδα της , αν και μόνον αν η πράξη της ορίζεται στο .
Απόδειξη: Αν , τότε ο ισχυρισμός του Θεωρήματος είναι φανερός.
Έστω ένα πεπερασμένο υποσύνολο της ομάδας στο οποίο ορίζεται η πράξη της , δηλαδή
| (2.1) |
Η πράξη στο είναι προσεταιριστική γιατί αυτό συμβαίνει στην . Επίσης για τον ίδιο λόγο επιτρέπεται η απλοποίηση αριστερά και δεξιά στο . Άρα ικανοποιούνται οι απαιτήσεις του Θεωρήματος 1.2.7 για να είναι το ομάδα, δηλαδή υποομάδα της .
Παραδείγματα 2.1.5
Το υποσύνολο , για , είναι υποομάδα της σύμφωνα με το Θεώρημα 2.1.3. Πράγματι; για ,
| (2.2) |
Το υποσύνολο της δεν είναι υποομάδα της . Όμως η πρόσθεση των ακέραιων αριθμών ορίζεται στο . Αυτό το παράδειγμα μας οδηγεί στο συμπέρασμα ότι η συνθήκη ((πεπερασμένο)) είναι απαραίτητη στο Θεώρημα 2.1.4.
Έστω . Το υποσύνολο είναι υποομάδα της γιατί ο πολλαπλασιασμός ορίζεται σε αυτό σύμφωνα με το Θεώρημα 2.1.4.
Στην ομάδα συμμετρίας του ισόπλευρου τριγώνου (βλέπε Παράδειγμα 1.1.4.3) το σύνολο των στροφών του αποτελεί υποομάδα της .
Το ίδιο συμβαίνει με το σύνολο για την ομάδα συμμετρίας του τετραγώνου (βλέπε Παράδειγμα 1.1.4.4).
Έστω ένας πρώτος φυσικός αριθμός και
| (2.3) |
Το με πράξη την πρόσθεση των μιγαδικών αριθμών αποτελεί αβελιανή ομάδα. Είναι εύκολο να διαπιστωθεί ότι
| (2.4) |
για , πρώτους φυσικούς αριθμούς τέτοιους ώστε .
Ακόμη
| (2.5) |
Έστω
| (2.6) |
όπου είναι σταθερός φυσικός αριθμός. Είναι εύκολο να δούμε ότι
| (2.7) |
όπου είναι η πολλαπλασιαστική ομάδα του Παραδείγματος 1.1.2.8.
Θεωρούμε την πολλαπλασιαστική ομάδα , βλ. Παράδειγμα 1.1.2.5 και την ειδική γραμμική ομάδα , βλέπε άσκηση του εδαφίου 1.1. Είναι φανερό ότι
| (2.8) |
Ακόμη μπορούμε να σχηματίσουμε το ακόλουθο διάγραμμα
| (2.9) |
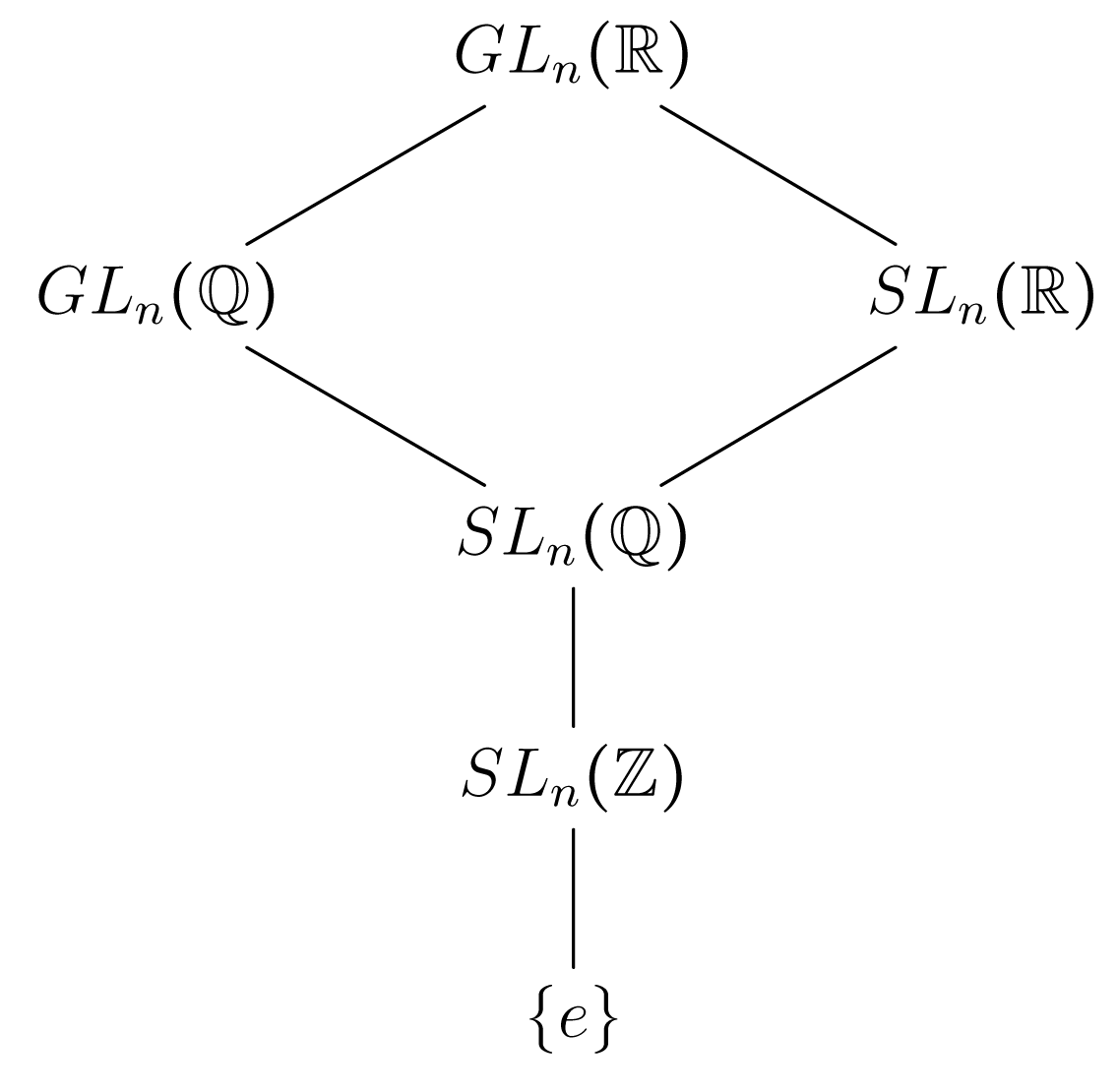 Σχήμα 2.1
Σχήμα 2.1με σχέση διάταξης τη σχέση εγκλεισμού . Ας παρατηρήσουμε ότι από τον ορισμό του αντίστροφου πίνακα αν , ισχύει ότι έτσι το παραπάνω διάγραμμα στο Σχήμα 2.1 είναι διάγραμμα υποομάδων της .
Θεωρούμε, τώρα, τα επόμενα υποσύνολα του .
-
•
, το σύνολο των διαγώνιων πινάκων (diagonal matrices), δηλαδή των πινάκων που κάθε στοιχείο τους εκτός της κύριας διαγωνίου είναι μηδέν.
-
•
, το σύνολο όλων των άνω τριγωνικών πινάκων (upper trigonal matrices), δηλαδή των πινάκων που έχουν όλα τους τα στοιχεία κάτω από την κύρια διαγώνιο ίσα με μηδέν. Ανάλογα ορίζεται το σύνολο των κάτω τριγωνικών πινάκων (low trigonal matrices).
-
•
, το σύνολο όλων των πινάκων με όλα τα στοιχεία κάτω από την κύρια διαγώνιο ίσα με μηδέν και με όλα τα στοιχεία πάνω στην κύρια διαγώνιο ίσα με .
Είναι εύκολο να διαπιστώσουμε ότι
| (2.10) |
και
| (2.11) |
Η ομάδα λέγεται διαγώνιος (diagonal) ομάδα (των -πινάκων με συντελεστές από το ), η λέγεται άνω τριγωνική ομάδα (upper diagonal) και η μοναδοτριγωνική (unidiagonal) ομάδα.
Θεωρούμε το πολυώνυμο ανεξάρτητων μεταβλητών
| (2.12) |
Παρατηρούμε ότι στο γινόμενο ο παράγων , για και , εμφανίζεται ακριβώς μία φορά. Αν , βλέπε Παράδειγμα 1.1.2.7, ορίζουμε το πολυώνυμο
| (2.13) |
Βλέπουμε ότι κάθε παράγων , για και , εμφανίζεται ακριβώς μία φορά στο πολυώνυμο .
Όμως, είναι δυνατόν στο πολυώνυμο αντί του , για , να υπάρχει το . Έτσι τα δύο πολυώνυμα και διαφέρουν μόνο στο πρόσημο, δηλαδή .
Ορισμός 2.1.6
Η μετάθεση λέγεται άρτια (even) αν
| (2.14) |
και περιττή (odd) αν
| (2.15) |
Έστω , παρατηρούμε ότι
Έτσι φαίνεται αμέσως ότι αν οι μεταθέσεις , είναι και οι δύο άρτιες ή και οι δύο περιττές, τότε η μετάθεση είναι άρτια, ενώ αν η μία είναι άρτια και η άλλη περιττή, τότε η σύνθεσή τους είναι περιττή μετάθεση. Ας θεωρήσουμε, τώρα, το σύνολο όλων των άρτιων μεταθέσεων του . Αν , τότε, όπως είδαμε, . Άρα σύμφωνα με το Θεώρημα 2.1.4 το είναι υποομάδα της .
Έστω ένας μετρικός χώρος (metric space) με μετρική , δηλαδή ένα σύνολο για το οποίο ορίζεται μία συνάρτηση που ικανοποιεί τις ιδιότητες:
-
, για , ,
-
,για .
Μία αμφιμονότιμη και επί συνάρτηση λέμε ότι διατηρεί τη δομή του μετρικού χώρου αν
| (2.16) |
για . Μία τέτοια συνάρτηση λέγεται ισομετρία (isometry) του . Π.χ. η διατήρηση των αποστάσεων σημείων στο επίπεδο είναι μία ισομετρία του επιπέδου. Συμβολίζουμε με το σύνολο των ισομετριών του . Είναι φανερό ότι
| (2.17) |
(βλέπε Παράδειγμα 1.1.2.6). Θα αποδείξουμε ότι
| (2.18) |
Έστω , τότε, για όλα τα , ισχύει
| (2.19) |
Άρα η , για όλα τα , και σύμφωνα με το Θεώρημα 2.1.4 αποδείξαμε ότι
| (2.20) |
Για τις ισομετρίες παραπέμπουμε τον αναγνώστη στο [ΘΧΒ] και στο [Στ]. Στη συνέχεια αναφέρουμε τρεις ισομετρίες του ευκλείδειου χώρου ([Art], ch.5) , δηλαδή του -διανυσματικού χώρου εφοδιασμένου με ένα εσωτερικό γινόμενο.
Α. Μετατόπιση (Translation) Μία συνάρτηση λέγεται μετατόπιση, αν απεικονίζει το τυχαίο στοιχείο στο σημείο που βρίσκεται σε σταθερή απόσταση από το και σε σταθερή κατεύθυνση. Η αναλυτική έκφραση μιάς μετατόπισης είναι
| (2.21) |
όπου είναι ένα σταθερό στοιχείο του και θα τη συμβολίζουμε με . Συμβολίζουμε με
| (2.22) |
το σύνολο όλων των μετατοπίσεων του Ευκλείδειου χώρου . Είναι φανερό ότι . Θα αποδείξουμε ότι
| (2.23) |
Πράγματι; έστω , τότε, για κάθε , έχουμε
| (2.24) |
Άρα
| (2.25) |
δηλαδή
| (2.26) |
Ακόμη παρατηρούμε ότι, για όλα τα , ισχύει
| (2.27) |
δηλαδή , για όλα τα .
Συμπέρασμα: H είναι μία αβελιανή υποομάδα της .
Β. Κατοπτρισμός (Reflection) Μία συνάρτηση λέγεται κατοπτρισμός, αν υπάρχει μία ευθεία γραμμή του τέτοια ώστε η να απεικονίζει το τυχαίο σημείο του στην καθρεφτκή του εικόνα ως προς την ευθεία . Αν επιλέξουμε ως τον άξονα , τότε η αναλυτική έκφραση της είναι η
| (2.28) |
για . Παρατηρούμε ότι και εύκολα διαπιστώνουμε ότι .
Γ. Στροφή (Rotation) Έστω ένα σταθερό σημείο του . Η στροφή του με κέντρο το κατά γωνία και φορά αντίστροφη των δεικτών του ρολογιού συμβολίζεται με . Η αναλυτική έκφραση της , αν τα στοιχεία δοθούν σε πολικές συντεταγμένες, είναι
| (2.29) |
Είναι φανερό ότι , . Παρατηρούμε ότι κάθε στροφή με κέντρο το εκφράζεται μοναδικά με τη μορφή , όπου , γιατί αν και μόνον αν το είναι ακέραιο πολλαπλασίο του . Συμβολίζουμε με
| (2.30) |
Αν , είναι δύο τυχαία στοιχεία του , τότε
| (2.31) |
Έτσι
| (2.32) |
Επομένως από το Θεώρημα 2.1.4 προκύπτει ότι
| (2.33) |
Χωρίς απόδειξη αναφέρουμε το επόμενο θεώρημα (βλ. [Στ], [Art])
Θεώρημα 2.1.7
Οι μετατοπίσεις, οι κατοπτρισμοί και οι στροφές είναι ισομετρίες του Ευκλείδειου χώρου . Ακόμη
| (2.34) |
όπου είναι ένας τυχαίος κατοπτρισμός,
| (2.35) |
και
| (2.36) |
Έστω ένας μετρικός χώρος (βλέπε Παράδειγμα 2.1.5.10) και μετρικός υποχώρος του (δηλαδή διανυσματικός υποχώρος του με την ίδια μετρική). Σχηματίζουμε το σύνολο
| (2.37) |
Είναι εύκολο να αποδείξει ο αναγνώστης ότι
| (2.38) |
Η ομάδα λέγεται ομάδα συμμετρίας (symmetry group) του σχετικά με τον μετρικό χώρο .
Η Διεδρική ομάδα (Dyhedral group) . Η διεδρική ομάδα, που αμέσως θα ορίσουμε, είναι μία ειδική περίπτωση του προηγούμενου παραδείγματος, δηλαδή μία ομάδα συμμετρίας. Θεωρούμε ένα κανονικό πολύγωνο στον Ευκλείδειο χώρο με πλευρές, όπου και την ομάδα συμμετρίας , η οποία είναι υποομάδα της . Συμβολίζουμε
| (2.39) |
Θα υπολογίσουμε την σύμφωνα με το Θεώρημα 2.1.7. Η ομάδα συμμετρίας του σχετικά με τον Ευκλείδειο χώρο αποτελείται από τις ισομετρίες του που έχουν την ιδιότητα . Έτσι, σύμφωνα με το Θεώρημα 2.1.7, το σύνολο είναι το , όπου είναι το σύνολο των στροφών του που έχουν την ιδιότητα και ένας κατοπτρισμός του για τον οποίο . Είναι φανερό ότι καμμία μεταφορά (εκτός της ταυτοτικής) δεν ικανοποιεί τη σχέση . Τα στοιχεία του είναι ακριβώς οι στροφές ως προς το κέντρο του πολυγώνου κατά γωνία , . Ένας κατοπτρισμός ορίζεται ως προς τον άξονα που διέρχεται από το κέντρο του και από μία κορυφή του , αν το είναι περιττός, ή από το κέντρο και το μέσον μίας πλευράς, αν ο είναι άρτιος. Ας συμβολίσουμε με τη στροφή του ως προς το κέντρο του κατά γωνία , τότε το
| (2.40) |
και
| (2.41) |
Όπως είδαμε από το προηγούμενο παράδειγμα το αποτελεί ομάδα με πράξη τη σύνθεση συναρτήσεων με τάξη . Η ομάδα λέγεται διεδρική ομάδα τάξης .
Μπορούμε εύκολα να αποδείξουμε ότι
| (2.42) |
εφαρμόζοντας το Θεώρημα 2.1.7 (αυτό έχει ήδη γίνει στο Παράδειγμα για τη γενικότερη περίπτωση).
Ας επανέλθουμε στη . Από τον ορισμό των κατοπτρισμών διαπιστώνουμε ότι τα στοιχεία του συνόλου
| (2.43) |
είναι κατοπτρισμοί ως προς διαφορετικούς άξονες. Αυτό σημαίνει (γεωμετρικά) ότι
| (2.44) |
άρα, και
| (2.45) |
Επομένως τα στοιχεία της ικανοποιούν τις σχέσεις
| (2.1.2) |
Ακόμη είναι φανερό ότι η ομάδα δεν είναι αβελιανή, ενώ οι υποομάδες της
| (2.47) |
είναι αβελιανές.
Μετά τον ορισμό της υποομάδας είναι φυσικό να αναρωτηθούμε αν μπορούμε να δημιουργήσουμε νέες υποομάδες από δοσμένες υποομάδες. Π.χ. η ένωση ή η τομή υποομάδων είναι υποομάδες της αρχικής ομάδας; Οι επόμενες προτάσεις απαντούν στον παραπάνω προβληματισμό.
Πρόταση 2.1.8
Έστω μία οικογένεια υποομάδων μίας ομάδας , όπου είναι ένα μη κενό σύνολο. Τότε
| (2.48) |
Απόδειξη: Έστω . Είναι φανερό ότι το είναι ένα μη κενό υποσύνολο της . Έστω , τότε για όλα τα . Άρα σύμφωνα με το Θεώρημα 2.1.3 ισχύει ότι για όλα τα . Επομένως , δηλαδή .
Πρόταση 2.1.9
Η ένωση δύο υποομάδων και μίας ομάδας είναι υποομάδα της αν και μόνον αν ή .
Απόδειξη: Είναι φανερό ότι για τις υποομάδες και της αν ισχύει μία από τις σχέσεις ή , τότε . Ας υποθέσουμε αντίστροφα, ότι . Σύμφωνα με το Θεώρημα 2.1.3 αν , τότε . Ας θεωρήσουμε και , τότε ή . Αν , δηλαδή το τυχαίο στοιχείο της ανήκει στο . Άρα . Αν , τότε , για το τυχαίο . Άρα . Επομένως ή .
Γενικότερα ισχύει η επόμενη Πρόταση.
Πρόταση 2.1.10
Έστω μία οικογένεια υποομάδων μίας ομάδας , που έχει την ιδιότητα για κάθε ζεύγος υποομάδων του συνόλου η μία από τις δύο να περιέχει την άλλη. Τότε η
είναι υποομάδα της .
Η απόδειξη αφήνεται για τον αναγνώστη.
Παραδείγματα 2.1.11
Θεωρούμε την υποομάδα του Παραδείγματος της σελίδας 2.1.5, όπου είναι ένας πρώτος φυσικός αριθμός. Σύμφωνα με την Πρόταση 2.1.8
| (2.49) |
όπου το διατρέχει όλους τους πρώτους φυσικούς αριθμούς. Είναι φανερό ότι . Θα αποδείξουμε ότι . Έστω , τότε για δύο διακεκριμένους πρώτους ισχύει ότι . Άρα υπάρχουν ώστε
| (2.50) |
δηλαδή .
Θεωρούμε την υποομάδα της πολλαπλασιαστικής ομάδας του Παραδείγματος 2.1.5.6. Σύμφωνα με την Πρόταση 2.1.10
| (2.51) |
όπου το διατρέχει τα στοιχεία του .
Έστω, τώρα, μία ομάδα και . Θεωρούμε το σύνολο
| (2.52) |
όλων των ακεραίων δυνάμεων του στοιχείου . Εφαρμόζοντας το Θεώρημα 2.1.3 αποδεικνύουμε αμέσως ότι το αποτελεί υποομάδα της . Επομένως κάθε στοιχείο δημιουργεί την υποομάδα της .
Είναι δυνατόν και αυτό συμβαίνει αν και μόνον αν . Είναι δυνατόν για κάποιο στοιχείο της; Ναι, η ομάδα
| (2.53) |
Ορισμός 2.1.12
Μία ομάδα λέγεται κυκλική (cyclic) αν υπάρχει στοιχείο της τέτοιο ώστε
| (2.54) |
Το στοιχείο λέγεται παράγον στοιχείο (generator) της .
Παρατηρούμε , αφού , δηλαδή το παράγον στοιχείο δεν ορίζεται μοναδικά για μία κυκλική ομάδα.
Παραδείγματα 2.1.13
Η πολλαπλασιαστική ομάδα είναι κυκλική, αφού παράγεται από το . Επίσης . Όμως η
Η υποομάδα των στροφών του κανονικού πολυγώνου (βλ. Παράδειγμα 2.1.5.12) είναι κυκλική που παράγεται από το στοιχείο και
Η μετάθεση παράγει την υποομάδα
| (2.55) |
της . Πράγματι δεν υπάρχουν άλλες διακεκριμένες δυνάμεις του , γιατί αν τότε από την ευκλείδεια διαίρεση , . Επομένως
| (2.56) |
δηλαδή οι διακεκριμένες δυνάμεις του είναι οι: .
Η ομάδα είναι κυκλική γιατί
| (2.57) |
Στο επόμενο εδάφιο θα ασχοληθούμε περισσότερο με τις κυκλικές ομάδες. Τώρα θα γενικεύσουμε τον Ορισμό 2.1.12. Παρατηρούμε ότι η ομάδα δεν είναι κυκλική, γιατί δεν υπάρχει ένα στοιχείο της, έστω , ώστε κάθε στοιχείο της να είναι δύναμη του . Αυτό το διαπιστώνουμε από τον πίνακα του Cayley της (βλ. Παράδειγμα 1.1.4.3). Ακόμη, όμως, παρατηρούμε ότι κάθε στοιχείο της είναι γινόμενο δυνάμεων του και του . Με αφορμή τις παρατηρήσεις αυτές οδηγούμαστε στον επόμενο ορισμό.
Ορισμός 2.1.14
Έστω μία ομάδα. Ένα υποσύνολο του λέγεται σύνολο παραγόντων στοιχείων (set of generators) της και συμβολίζουμε , αν
| (2.58) |
Παραδείγματα 2.1.15
Ας θεωρήσουμε την ομάδα , βλέπε Παράδειγμα 1.1.2.7. Η έχει στοιχεία, ας συμβολίσουμε με και με . Υπολογίζουμε τον πίνακα Cayley της προκειμένου να βρούμε ένα παράγον σύνολο της . Φυσικά για την μας βοηθά το γεγονός ότι έχει μικρή τάξη. Όπως είδαμε , .
Ακόμη υπολογίζουμε ότι
| (2.59) |
Άρα
| (2.1.3) |
Ο πίνακας Cayley της εύκολα υπολογίζεται (με τους απαραίτητους υπολογισμούς) ότι είναι ο Πίνακας 2.1.

Πίνακας 2.1 |
(2.61) |
Από το σύνολο στη σχέση (2.1.3) προκύπτει ότι , δηλαδή το σύνολο είναι παράγον σύνολο για την . Αλλά ακόμη με τη βοήθεια του πίνακα Cayley μπορούμε να διαπιστώσουμε ότι
| (2.62) |
Μπορούμε να υπολογίσουμε και άλλα παράγοντα σύνολα με δύο στοιχεία της , ενώ καταλαβαίνουμε ότι παράγοντα σύνολα με περισσότερα από δύο στοιχεία υπάρχουν, αλλά δεν είναι τόσο χρήσιμα. Από τους υπολογισμούς φαίνεται ότι όσο μικρότερο παράγον σύνολο εντοπίσουμε για μία ομάδα τόσο καλύτερο και ταχύτερο αποτέλεσμα έχουμε για τον χειρισμό της ομάδας.
Η διεδρική ομάδα παράγεται από τα στοιχεία , (βλ. Παράδειγμα 1.1.4.3), όπως διαπιστώνεται από τον πίνακα Cayley. Όμοια η έχει παράγον σύνολο το (βλ. Παράδειγμα 1.1.4.4).
Ας δούμε την ομάδα . Ένας τυχαίος ρητός αριθμός έχει τη μορφή , όπου και , δηλαδή είναι ακέραιο πολλαπλάσιο του . Άρα
| (2.63) |
Από το θεμελιώδες θεώρημα της Αριθμητικής γνωρίζουμε ότι κάθε ρητός αριθμός γράφεται ως
| (2.64) |
όπου , , είναι πρώτοι φυσικοί αριθμοί, και . Άρα
| (2.65) |
Από τα παραπάνω παραδείγματα βλέπουμε ότι υπάρχουν άπειρης τάξης ομάδες με μονοσύνολο παράγον σύνολο όπως η ή μία κυκλική ομάδα άπειρης τάξης. Υπάρχουν ομάδες άπειρης τάξης που έχουν παράγον σύνολο με άπειρο πλήθος στοιχείων, όπως η και η . Καταλαβαίνουμε ότι το παράγον σύνολο δίνει σημαντικές πληροφορίες για την ομάδα, όμως η εύρεση παραγόντων συνόλων με συγκεκριμένες ιδιότητες είναι πολλές φορές δυσεπίλυτο πρόβλημα.
Ασκήσεις
1. Δίνεται ένα μη κενό σύνολο και ένας θετικός πραγματικός αριθμός . Να αποδείξετε ότι η συνάρτηση
| (2.66) |
είναι μία μετρική στο . Ακόμη να αποδείξετε ότι, για τον μετρικό χώρο , ισχύει .
2. Θεωρούμε το σύνολο των πραγματικών αριθμών ως Ευκλείδειο χώρο διάστασης . Ο με μετρική τη , , γίνεται ένας μετρικός χώρος. Να αποδείξετε ότι:
-
Για κάθε , η συνάρτηση
(2.67) είναι μία ισομετρία.
-
Για κάθε , η συνάρτηση
(2.68) είναι μία ισομετρία και ακόμη ότι
(2.69) -
Κάθε ισομετρία του είναι μία μετατόπιση ή ένας κατοπτρισμός.
-
Το σύνολο αποτελεί αντιμεταθετική υποομάδα της .
-
Αν ορίσουμε , , τότε
(2.70)
3. Με τους συμβολισμούς του Παραδείγματος
2.1.5.10 να εξετάσετε αν το
αποτελεί υποομάδα της .
4. Έστω μία ομάδα και . Να αποδείξετε ότι το είναι υποομάδα της .
5. Έστω μία ομάδα και . Να αποδείξετε ότι το αποτελεί υποομάδα της , . Η υποομάδα λέγεται συζυγής (conjugate) υποομάδα της .
2.2 Τάξη στοιχείου - Κυκλικές ομάδες
Από τα παραδείγματα των κυκλικών ομάδων που αναφέραμε στο Εδάφιο 2.1 είδαμε ότι υπάρχουν πεπερασμένες κυκλικές ομάδες, όπως η , όπου και , και υπάρχουν άπειρες κυκλικές ομάδες, όπως η .
Εδώ θα εξετάσουμε λεπτομερέστερα τις κυκλικές ομάδες.
Ας θεωρήσουμε μία ομάδα και . Έστω
| (2.71) |
η υποομάδα της που παράγεται από το στοιχείο της . Ας υποθέσουμε ότι η έχει πεπερασμένη τάξη, δηλαδή . Αυτό σημαίνει ότι όλες οι ακέραιες δυνάμεις του δεν είναι διακεκριμένες. Επομένως υπάρχουν τουλάχιστον δύο ακέραιοι , τέτοιοι ώστε και
| (2.72) |
Αν τότε . Αν , τότε από τη σχέση και , δηλαδή . Συμπαιρένουμε, έτσι, ότι σε κάθε περίπτωση υπάρχει φυσικός αριθμός, έστω ( ή ), ώστε . Θεωρούμε το σύνολο
| (2.73) |
Το είναι μη κενό υποσύνολο του συνόλου των φυσικών αριθμών, επομένως έχει ένα ελάχιστο στοιχείο, έστω . Έτσι, είναι ο ελάχιστος διάφορος του μηδενός φυσικός αριθμός ώστε . Θα υπολογίσουμε, τώρα, με τη βοήθεια του όλες τις διακεκριμένες δυνάμεις του , δηλαδή όλα τα στοιχεία της κυκλικής ομάδας . Έστω ένα τυχαίο στοιχείο της , από τον αλγόριθμο του Ευκλείδη προκύπτει ότι υπάρχουν μοναδικοί φυσικοί αριθμοί και , ωστε , με . Επομένως
| (2.74) |
Άρα οι δυνατές διακεκριμένες δυνάμεις του είναι οι
| (2.75) |
δηλαδή
| (2.76) |
Ακόμη από τα παραπάνω παρατηρούμε ότι
| (2.77) |
και
| (2.78) |
Αν, τώρα, η υποομάδα έχει άπειρο πλήθος στοιχείων, τότε όλες οι ακέραιες δυνάμεις του είναι διακεκριμένες, δηλαδή
| (2.79) |
Πράγματι, αν υπάρχουν ακέραιοι ώστε , τότε, όπως παραπάνω, θα οδηγούμασταν στο συμπέρασμα ότι τα στοιχεία της θα ήταν πεπερασμένου πλήθους. Επομένως, αν , τότε, για ακεραίους , ,
| (2.80) |
Από τα παραπάνω φαίνεται η ανάγκη του επόμενου ορισμού.
Ορισμός 2.2.1
Έστω ένα στοιχείο μίας ομάδας . Ο ελάχιστος διάφορος του μηδενός φυσικός αριθμός , αν υπάρχει, για τον οποίο λέγεται τάξη (order) του στοιχείου , συμβολίζεται με και λέμε ότι το στοιχείο έχει πεπερασμένη (finite) τάξη. Αν δεν υπάρχει τέτοιος φυσικός αριθμός για το στοιχείο , τότε λέμε ότι το στοιχείο έχει άπειρη (infinite) τάξη και συμβολίζουμε .
Από όσα προηγήθηκαν του ορισμού 2.2.2 αποδείχθηκε η επόμενη πρόταση
Πρόταση 2.2.2
Έστω μία ομάδα και .
-
αν και , τότε
(2.81) και αν , τότε
(2.82) -
Έστω . Τότε, για
(2.83) και ιδιαίτερα
(2.84) -
Έστω . Τότε, για
(2.85)
Παραδείγματα 2.2.3
Το ουδέτερο στοιχείο μίας ομάδας είναι το μόνο στοιχείο με τάξη ίση με . Πράγματι αν και .
Στην κυκλική ομάδα το στοιχείο έχει άπειρη τάξη. Αλλά και κάθε ακέραιος έχει άπειρη τάξη, αφού αν , τότε
| (2.86) |
Όμως, αν , τότε .
Στην κυκλική ομάδα άπειρης τάξης, δηλαδή , κάθε στοιχείο , έχει άπειρη τάξη. Πράγματι; αν , τότε
| (2.87) |
δηλαδή οι δυνάμεις του δεν είναι διακεκριμένες, ισοδύναμα το οποίον είναι αδύνατον.
Στην ομάδα (βλ. Παράδειγμα 2.1.13.1), παρατηρούμε ότι και .
Παίρνουμε το Παράδειγμα 1.2.8.1. Στην ομάδα του Πίνακα 1.12, βλέπουμε ότι
| (2.88) |
Στην ομάδα του Πίνακα 1.13, βλέπουμε ότι
| (2.89) |
και ακόμη η ομάδα αυτή είναι κυκλική, παράγεται από το ή από το , δηλαδή
| (2.90) |
Για τις ομάδες των Πινάκων 1.14 και 1.15 παρατηρούμε ότι είναι επίσης κυκλικές, αυτή με πίνακα Cayley τον πίνακα παράγεται από το ή από το , ενώ αυτή του Πίνακα 1.15 παράγεται από το ή το .
Στο Παράδειγμα 1.2.8.3 παρατηρούμε από τον πίνακα Cayley, βλ. Πίνακα 1.17, ότι
| (2.91) |
και
| (2.92) |
Στην ομάδα (βλ. Παράδειγμα 1.1.4.3) βλέπουμε από τον πίνακα Cayley, βλ. Πίνακα 1.5, ότι
| (2.93) |
Θεωρούμε την ομάδα . Υπολογίζουμε τις τάξεις των στοιχείων της. Βλέπουμε ότι , και δεν υπάρχει φυσικός για τον οποίο . Άρα . Όμοια . Βέβαια η δεν είναι κυκλική, αφού δεν υπάρχει στοιχείο της που να την παράγει.
Ας δούμε τώρα, μερικές βασικές ιδιότητες της έννοιας της τάξης στοιχείου ομάδας.
Πρόταση 2.2.4
Έστω μία ομάδα.
-
, .
-
, .
-
, .
Απόδειξη: . Έστω . Αν , τότε (βλέπε Θεώρημα 1.3.2, i)
| (2.94) |
αυτό, όμως, είναι άτοπο, γιατί . Άρα και .
Έστω ότι και . Τότε
| (2.95) |
Όμοια από τη σχέση
| (2.96) |
Οι σχέσεις και για τους φυσικούς αριθμούς και οδηγούν στη σχέση . Άρα σε κάθε περίπτωση και αποδείχθηκε η .
. Η απόδειξη είναι ανάλογη με αυτή του , αρκεί να παρατηρήσουμε ότι
| (2.97) |
Οι λεπτομέρειες αφήνονται για τον αναγνώστη.
. Έστω και . Τότε
| (2.98) |
Όμοια , άρα . Η περίπτωση αντιμετωπίζεται όπως στο και αφήνεται για τον αναγνώστη.
Πρόταση 2.2.5
Έστω μία κυκλική ομάδα. Τότε
-
Αν , τότε για κάθε , ισχύει
(2.99) όπου και , .
-
Αν τότε η παράγεται από το ή από το .
Απόδειξη: Έστω ότι . Επειδή οι αριθμοί και είναι ακέραιοι, έχουμε
| (2.100) |
Επομένως, αφού , έπεται ότι .
Ακόμη,
| (2.101) |
και επειδή οι αριθμοί και είναι πρώτοι μεταξύ τους, προκύπτει ότι . Τώρα, από τις σχέσεις και έπεται ότι
| (2.102) |
και αποδείχθηκε το .
Τώρα, ας παρατηρήσουμε ότι αν είναι μία πεπερασμένη κυκλική ομάδα με και είναι ένα επίσης παράγον στοιχείο της , τότε
| (2.103) |
Άρα
| (2.104) |
(βλέπε Πρόταση 2.2.2, ). Έτσι διαπιστώνουμε ότι κάθε παράγον στοιχείο της έχει τάξη . Εφαρμόζουμε τώρα στη παραπάνω διαπίστωση το , και βρίσκουμε ποιά είναι ακριβώς τα στοιχεία που παράγουν την . Είναι ακριβώς τα για τα οποία
| (2.105) |
Άρα
| (2.106) |
και αποδείχθηκε το i). Το ii) αφήνεται ως άσκηση για τον αναγνώστη.
Παραδείγματα 2.2.6
Ας θεωρήσουμε την ομάδα , η οποία όπως είδαμε είναι κυκλική και (βλ. Παράδειγμα 2.1.13.4) Από την Πρόταση 2.2.5, προκύπτει ότι
| (2.107) |
Στην ομάδα το στοιχείο έχει τάξη , ενώ .
Θεωρούμε την ομάδα , όπου είναι ένας πρώτος φυσικός αριθμός. Αν , τότε
| (2.108) |
Άρα κάθε στοιχείο της έχει τάξη , δηλαδή είναι παράγον στοιχείο της .
Πρόταση 2.2.7
Έστω μία ομάδα και δύο στοιχεία της πεπερασμένης τάξης έτσι ώστε
| (2.109) |
και
| (2.110) |
Τότε
| (2.111) |
Απόδειξη: Έστω ότι , και . Τότε επειδή , έχουμε
| (2.112) |
Άρα , δηλαδή .
Επίσης από τις σχέσεις και , έπεται ότι
| (2.113) |
άρα
| (2.114) |
Όμοια
| (2.115) |
άρα
| (2.116) |
Όμως , επομένως από τις σχέσεις και έπεται ότι και , δηλαδή . Οι σχέσεις και , οδηγούν στη σχέση , για τους φυσικούς αριθμούς . Έτσι αποδείχθηκε η πρόταση.
Το επόμενο συμπέρασμα δίνει μία σημαντική πληροφορία για τη δομή των κυκλικών ομάδων.
Θεώρημα 2.2.8
Κάθε υποομάδα κυκλικής ομάδας είναι κυκλική.
Απόδειξη: Έστω και μία γνήσια υποομάδα της . Τα στοιχεία της είναι δυνάμεις του , έστω, λοιπόν, ότι
| (2.117) |
Το , αλλά στο υπάρχουν και φυσικοί αριθμοί. Πράγματι, αν , τότε . Έστω
| (2.118) |
Το έχει ένα ελάχιστο στοιχείο ως υποσύνολο του και έστω αυτό. Αν με , τότε υπάρχουν μοναδικοί φυσικοί αριθμοί ώστε , με . Επομένως
| (2.119) |
γιατί . Όμως, από την επιλογή του και τις δυνατές τιμές που μπορεί να λάβει το , έπεται ότι . Άρα το τυχαίο στοιχείο του με θετικό εκθέτη είναι της μορφής . Αυτό σημαίνει ότι το τυχαίο στοιχείο του είναι δύναμη του , αφού . Άρα το περιέχει δυνάμεις του και αφού είναι ομάδα, ως υποομάδα της , περιέχει όλες τις δυνάμεις του , δηλαδή . Αποδείχθηκε έτσι το θεώρημα.
Παρατήρηση 2.2.9
Θα πρέπει να παρατηρήσουμε ότι το αντίστροφο του Θεωρήματος 2.2.8 δεν ισχύει. Αν, δηλαδή, κάθε υποομάδα μίας ομάδας είναι κυκλική δεν έπεται ότι η είναι κυκλική.
Π.χ. η έχει την ιδιότητα κάθε υποομάδα της να είναι κυκλική (βλέπε Παράδειγμα 2.1.15.1), όμως η δεν είναι κυκλική.
Παράδειγμα 2.2.10
Συμπέρασμα: Η έχει δύο μόνον υποομάδες την και τον εαυτό της.
2. Έστω ένας πρώτος φυσικός αριθμός. Τότε
(Θεώρημα του Wilson). Πράγματι, θεωρούμε την πολλαπλασιαστική ομάδα Κάθε στοιχείο της , έχει αντίστροφο, επίσης μόνον τα στοιχεία 1 και -1 ταυτίζονται με το αντίστροφό τους. Άρα στο γινόμενο αφού τα άλλα στοιχεία θα απλοποιηθούν. Άρα
Ασκήσεις
1. Να υπολογίσετε την τάξη κάθε στοιχείου της . Είναι η κυκλική;
2. Να ολοκληρωθεί η απόδειξη της Πρότασης 2.2.4.
3. Να αποδείξετε οτι τα στοιχεία και της ομάδας έχουν τάξη , ενώ .
4. Να εξηγήσετε αν ισχύει η επόμενη πρόταση: Αν η είναι μία ομάδα τάξης , τότε υπάρχει στοιχείο με .
5. Να αποδείξετε ότι αν είναι μία αβελιανή ομάδα, το σύνολο των στοιχείων της με πεπερασμένη τάξη είναι υποομάδα της . Η πρόταση αυτή ισχύει για μη αβελιανές ομάδες;
(Υπόδειξη: βλ. άσκηση 3)
6. Να αποδείξετε ότι μία ομάδα με τάξη άρτιο αριθμό περιέχει περιττό πλήθος στοιχείων τάξης ισης με .
7. Να υπολογίσετε όλες τις υποομάδες της .
8. Να υπολογίσετε όλες τις υποομάδες της .
2.3 Ομομορφισμοί ομάδων
Ας θεωρήσουμε τις ομάδες και . Όπως έχουμε διαπιστώσει είναι και οι δύο κυκλικές ομάδες τάξης και , ενώ . Αν σχηματίσουμε τον πίνακα Cayley για κάθε μία από αυτές τις ομάδες θα διαπιστώσουμε ότι αν αλλάξουμε την ονομασία των στοιχείων της ομάδας ως εξής: καλέσουμε το , το , το και το , τότε ο πίνακας Cayley της γίνεται ο πίνακας Cayley της . Το γεγονός αυτό το περιγράφουμε λέγοντας ότι οι ομάδες και είναι ισόμορφες. Ας δούμε ουσιαστικά τι κάναμε παραπάνω. Ορίσαμε μία συνάρτηση με κανόνα
| (2.120) |
Η συνάρτηση είναι προφανώς αμφιμονότιμη και επί. Ακόμη είναι εύκολο να δούμε ότι αν, για , τότε , (η είναι προσθετική και η πολλαπλασιαστική). Η συνάρτηση παρατηρούμε ότι ουσιαστικά διατηρεί τη δομή των δύο ομάδων. Δοκιμάζοντας με άλλες συναρτήσεις από τη στην είναι εύκολο να δούμε ότι δεν θα έχουμε το ίδιο αποτέλεσμα.
Σε αυτό το εδάφιο εξετάζουμε τέτοιες συναρτήσεις, όπως η , αλλά και γενικότερες όπως είναι οι ομομορφισμοί ομάδων, δηλαδή συναρτήσεων που δεν διατηρούν πλήρως τη δομή του προτύπου και της εικόνας. Τέτοιες συναρτήσεις μας βοηθούν γνωρίζοντας ιδιότητες της ομάδας πρότυπο να ανακαλύψουμε αντίστοιχες ιδιότητες της ομάδας εικόνας. Με άλλα λόγια να συγκρίνουμε μεταξύ τους ομάδες.
Ορισμός 2.3.1
Έστω και δύο ομάδες. Μία συνάρτηση λέγεται ομομορφισμός (homomorphism) από την ομάδα στην ομάδα αν
| (2.3.1) |
για όλα τα .
Στη σχέση (2.3.1) το γινόμενο ορίζεται ως προς την πράξη της , ενώ το γινόμενο ορίζεται ως προς την πράξη της .
Ιδιαίτερη ονομασία δίνουμε στον ομομορφισμό ανάλογα με τις ιδιότητες που έχει η συνάρτηση , έτσι προκύπτει ο επόμενος ορισμός.
Ορισμός 2.3.2
Έστω ένας ομομορφισμός της ομάδας στην ομάδα . Ο λέγεται επιμορφισμός (epimorphism), αν η συνάρτηση είναι επί. Ο λέγεται μονομορφισμός (monomorphism), αν η συνάρτηση είναι αμφιμονότιμη. Ο λέγεται ισομορφισμός (isomorphism), αν η συνάρτηση είναι αμφιμονότιμη και επί. Ιδιαίτερη ορολογία έχουμε όταν . Ο ομομορφισμός λέγεται ενδομορφισμός (endomorphism) της . Ο ισομορφισμός λέγεται αυτομορφισμός (automorphism) της . Δύο ομάδες και λέγονται ισόμορφες (isomorphic) αν υπάρχει ισομορφισμός και συμβολίζουμε . Αν υπάρχει μονομορφισμός , τότε λέμε ότι η ομάδα εμφυτεύεται στην και συμβολίζουμε , επίσης ο μονομορφισμός λέγεται εμφύτευση (embedding).
Παραδείγματα 2.3.3
Για κάθε φυσικό αριθμό , η συνάρτηση
| (2.122) |
είναι επιμορφισμός ομάδων (προσθετικών). Πράγματι, αν , τότε
| (2.123) |
Άρα η είναι ομομορφισμός ομάδων. Η είναι επί συνάρτηση. Πράγματι, αν , τότε υπάρχει το ώστε . Επομένως η είναι επιμορφισμός.
Η συνάρτηση
| (2.124) |
είναι επιμορφισμός πολλαπλασιαστικών ομάδων.
Η συνάρτηση
| (2.125) |
είναι επιμορφισμός ομάδων.
Αν είναι φυσικός αριθμός, η συνάρτηση
| (2.126) |
είναι επιμορφισμός πολλαπλασιαστικών ομάδων. Πράγματι, αν , τότε
| (2.127) |
δηλαδή η είναι ομομορφισμός ομάδων. Η είναι επί συνάρτηση, γιατί αν , τότε υπάρχει ο πίνακας
| (2.128) |
Ας παρατηρήσουμε εδώ ότι η είναι μη αβελιανή, για κάθε , ενώ η είναι αβελιανή ομάδα. Ακόμη για , η είναι ισομορφισμός ομάδων.
Ας δούμε μερικές βασικές ιδιότητες των ομομορφισμών ομάδων.
Πρόταση 2.3.4
Έστω ένας ομομορφισμός ομάδων. Τότε τα επόμενα ισχύουν
-
i.
Το είναι το ουδέτερο στοιχείο της , όπου είναι το ουδέτερο στοιχείο της .
-
ii.
, όπου .
-
iii.
Αν , τότε η .
Απόδειξη: Έστω , τότε
| (2.129) |
Όμως, στην ομάδα επιτρέπεται η απλοποίηση, άρα από την τελευταία σχέση έπεται ότι το είναι το ουδέτερο στοιχείο της .
Έστω , τότε
| (2.130) |
και επειδή από το το είναι το ουδέτερο στοιχείο της , από την τελευταία σχέση προκύπτει ότι το είναι το αντίστροφο του στην .
Έστω . Γνωρίζουμε ότι . Έστω , τότε από το έχουμε
| (2.131) |
γιατί (βλέπε Θεώρημα 2.1.3). Άρα
| (2.132) |
δηλαδή , πάλι σύμφωνα με το Θεώρημα 2.1.3.
Πρόταση 2.3.5
-
i.
Η σύνθεση ομομορφισμών ομάδων, όταν αυτή ορίζεται, είναι επίσης ομομορφισμός ομάδων.
-
ii.
Συμβολίζουμε με το σύνολο των αυτομορφισμών μίας ομάδας . Το με πράξη τη σύνθεση συναρτήσεων αποτελεί ομάδα.
Απόδειξη: Έστω , , ομάδες και , δύο ομομορφισμοί ομάδων. Θα δείξουμε ότι η είναι ομομορφισμός ομάδων. Έστω , τότε
| (2.133) |
Άρα η είναι ομομορφισμός ομάδων.
Έστω μία ομάδα. Η σύνθεση αυτομορφισμών της είναι επίσης αυτομορφισμός της , όπως προκύπτει από το και τις ιδιότητες των συναρτήσεων. Άρα η σύνθεση συναρτήσεων είναι μία πράξη τστο σύνολο , η οποία είναι προσεταιριστική. Η ταυτότητα στο είναι φανερό ότι είναι το ουδέτερο στοιχείο της . Μένει να αποδείξουμε ότι αν , τότε η αντίστροφη συνάρτηση της ανήκει στο . Όμως, η είναι αμφιμονότιμη και επί συνάρτηση, άρα αρκεί να δείξουμε ότι η είναι ενδομορφισμός της . Έστω , τότε υπάρχουν στοιχεία τέτοια ώστε και , αφού η είναι επί συνάρτηση. 'ρα
| (2.134) |
δηλαδή η είναι ενδομορφισμός της και αποδείχθηκε το ii).
Παραδείγματα 2.3.6
Δίνεται ένας μονομορφισμός ομάδων , όπου η είναι μία αβελιανή ομάδα. Θα αποδείξουμε ότι και η είναι αβελιανή. Πράγματι; αφού η είναι ομομορφισμός και η είναι αβελιανή, τότε
| (2.135) |
Όμως, η είναι μονομορφισμός, δηλαδή η είναι αμφιμονότιμη, άρα από την τελευταία σχέση προκύπτει ότι , για όλα τα . Επομένως η είναι αβελιανή.
Θεωρούμε τη συνάρτηση
| (2.136) |
Η είναι αμφιμονότιμη συνάρτηση, αφού, για , έχουμε . Επίσης η είναι ομομορφισμός ομάδων. Πράγματι, για , ισχύει
| (2.137) |
| (2.138) |
Άρα η είναι μονομορφισμός ομάδων. Παρατηρούμε ότι, ενώ η είναι αβελιανή, δεν ισχύει το ίδιο για την . Με άλλα λόγια δεν ισχύει το συμπέρασμα του παραπάνω Παραδείγματος , αν η είναι αβελιανή.
Δίνεται η αβελιανή ομάδα και ο ομομορφισμός ομάδων . Θα αποδείξουμε ότι η είναι αβελιανή υποομάδα της . Πράγματι, από την Πρόταση 2.3.4, προκύπτει ότι η . Μένει να αποδείξουμε την αντιμεταθετικότητα της . Έστω , τότε
| (2.139) |
από τον ορισμό του συνόλου , έπεται ότι η είναι αβελιανή υποομάδα της . Δηλαδή, η αντιμεταθετικότητα μεταφέρεται στην .
Πρόταση 2.3.7
Η ομάδα εμφυτεύεται στην ομάδα αν και μόνον αν η είναι ισόμορφη με μία υποομάδα της .
Απόδειξη:
Αν η ομάδα εμφυτεύεται στην ομάδα , τότε υπάρχει ένας μονομορφισμός και (βλ. Πρόταση 2.3.4, ). Είναι φανερό ότι η συνάρτηση , είναι ισομορφισμός ομάδων. Άρα η είναι ισόμορφη μ,ε την υποομάδα της . Αντίστροφα, αν η είναι ισόμορφη με την ομάδα , τότε υπάρχει ισομορφισμός ομάδων και η συνάρτηση , είναι μονομορφισμός ομάδων.
Έστω ένας ομομορφισμός ομάδων. Όπως είδαμε ορισμένες ιδιότητες που έχουν κάποια στοιχεία ή υποσύνολα της ομάδας μεταφέρονται σε αντίστοιχες εικόνες της , όμως, όλες οι ιδιότητες της δεν μεταφέρονται στην . Αυτό θα αποδεικνύεται με την ανάπτυξη της θεωρίας. Ο ομομορφισμός είναι η έννοια που βοηθά στη σύγκριση μεταξύ των ομάδων. Είναι δε εύκολο να διαπιστώσει ο αναγνώστης ότι αν η είναι ισομορφισμός τότε όλες οι ιδιότητες της μεταφέρονται στην και αντίστροφα βέβαια. Γι’ αυτό στην ’λγεβρα γενικότερα ταυτίζουμε τις ισόμορφες αλγεβρικές δομές με την έννοια ότι αρκεί να ασχοληθούμε με μία από αυτές για να γνωρίζουμε τι συμβαίνει με κάθε ισόμορφή της. Το μεγάλο, επομένως, ερώτημα για τις ομάδες ιδιαίτερα είναι: ποιές είναι οι μη ισόμορφες ομάδες; Η απάντηση οδηγεί στην ταξινόμηση των ομάδων,αλλά η μέχρι σήμερα έρευνα βρίσκεται αρκετά μακριά από την πλήρη απάντηση. Προς αυτή την κατεύθυνση βρίσκεται το επόμενο σημαντικό θεώρημα.
Θεώρημα (Cayley) 2.3.8
Κάθε ομάδα εμφυτεύεται σε μία ομάδα μετασχηματισμών. Ιδιαίτερα κάθε πεπερασμένη ομάδα εμφυτεύεται στην ομάδα , όπου είναι η τάξη της .
Απόδειξη: Έστω μία ομάδα. Για κάθε στοιχείο ορίζουμε την αντιστοιχία
| (2.140) |
Είναι φανερό ότι η είναι αμφιμονότιμη συνάρτηση αφού, αν , τότε . Ακόμη η είναι επί συνάρτηση. Πράγματι, αν , τότε υπάρχει το στοιχείο , ώστε . Επομένως η είναι μία αμφιμονότιμη και επί συνάρτηση στο σύνολο , δηλαδή είναι ένας μετασχηματισμός του συνόλου , για κάθε . Θεωρούμε το σύνολο
| (2.141) |
Θα αποδείξουμε ότι το σύνολο με πράξη τη σύνθεση συναρτήσεων είναι μία ομάδα και θα συγκρίνουμε την με την ομάδα . Είναι φανερό ότι , όπου είναι η ομάδα μετασχηματισμών του συνόλου (βλ. Παράδειγμα 1.1.2.6). Αρκεί να δείξουμε ότι . Έστω , για δύο στοιχεία . Θα αποδείξουμε ότι σύμφωνα με το κριτήριο υποομάδας. Παρατηρούμε ότι, για ,
| (2.142) |
δηλαδή . Eπομένως . Άρα, για ,
| (2.143) |
δηλαδή
| (2.144) |
Επομένως . Ορίζουμε τώρα την αντιστοιχία
| (2.145) |
Θα αποδείξουμε ότι η είναι ισομορφισμός ομάδων. Πράγματι, αν , τότε εύκολα αποδεικνύεται ότι
| (2.146) |
Άρα, η είναι αμφιμονότιμη συνάρτηση, ενώ είναι φανερό ότι η είναι επί συνάρτηση. Τέλος η είναι ομομορφισμός ομάδων, γιατι, αν , τότε
| (2.147) |
Επομένως . Αποδείξαμε ότι
| (2.148) |
και το θεώρημα προκύπτει από την Πρόταση 2.3.5. Τέλος αν όλα τα παραπάνω τα εφαρμόσουμε για την περίπτωση που , τότε η είναι η ομάδα μετασχηματισμών των αντικειμένων, δηλαδή η . 'ρα
| (2.149) |
Ας παρατηρήσουμε σε αυτό το σημείο ότι όταν , τότε Επομένως για η ομάδα εμφυτεύεται στην , αλλά δεν είναι ισόμορφη με την . Επίσης, όταν η δεν είναι πεπερασμένη τότε η συνάρτηση
είναι μονομορφισμός ομάδων και όχι ισομορφισμός, αφού καθε μετασχηματισμός του συνόλου δεν είναι απαραίτητα της μορφής , για κάποιο , όπως εύκολα μπορεί να διαπιστώσει ο αναγνώστης.
Από το Θεώρημα του Cayley προκύπτει ότι αρκεί να μελετήσουμε τις ομάδες μετασχηματισμών και τις υποομάδες τους για να γνωρίζουμε όλες τις ομάδες. Ιδιαίτερα αρκεί να γνωρίζουμε την , για κάθε φυσικό αριθμό , και τις υποομάδες της για να γνωρίζουμε όλες τις πεπερασμένες ομάδες. Παρά την ιδιαίτερη αξία του Θεωρήματος του Cayley, η έρευνα στη θεωρία ομάδων αποδεικνύει συνεχώς ότι πρέπει να αναπτυχθούν και άλλες μέθοδοι προσέγγισης της θεωρίας ομάδων από τον περιορισμό στη μελέτη των ομάδων μετασχηματισμών.
Η επόμενη έννοια που θα μας απασχολήσει ουσιαστικά ((μετράει)) πόσο απέχει ένας ομομορφισμός ομάδων από το να είναι μονομορφισμός, εξ αυτού του λόγου παίζει σημαντικό ρόλο στην αναζήτηση των ιδιοτήτων ομάδων.
Ορισμός 2.3.9
Έστω ένας ομομορφισμός ομάδων. Πυρήνας (kernel) της και συμβολίζεται ορίζεται το σύνολο
| (2.150) |
Είναι φανερό ότι και , όπου είναι το ουδέτερο στοιχείο της , γι’ αυτό πολλοί συγγραφείς συμβολίζουν τον ως .
Πρόταση 2.3.10
Έστω ένας ομομορφισμός ομάδων. Τότε:
-
i.
,
-
ii.
αν και μόνον αν η είναι αμφιμονότιμη συνάρτηση.
Απόδειξη: Έστω , τότε
| (2.151) |
Άρα και από το κριτήριο υποομάδας έπεται ότι .
. Έστω . Αν , τότε
| (2.152) |
δηλαδή η είναι αμφιμονότιμη συνάρτηση. Αντίστροφα, έστω ότι η είναι αμφιμονότιμη συνάρτηση, τότε
| (2.153) |
Άρα
Μπορούμε να δούμε τώρα ένα πρώτο συμπέρασμα ταξινόμησης ομάδων που αναφέρεται στις κυκλικές ομάδες.
Θεώρημα 2.3.11
-
i.
Κάθε κυκλική ομάδα άπειρης τάξης είναι ισόμορφη με την .
-
ii.
Κάθε κυκλική ομάδα πεπερασμένης τάξης, έστω , είναι ισόμορφη με την .
Απόδειξη: Έστω μία πολλαπλασιαστική ομάδα άπειρης τάξης. Θεωρούμε την αντιστοιχία
| (2.154) |
Η είναι συνάρτηση. Πράγματι, αν , για κάποιους ακεραίους , τότε από τον ορισμό της άπειρης τάξης (βλέπε Πρόταση 2.2.2, ) έπεται ότι . Είναι φανερό ότι η είναι αμφιμονότιμη, αφού . Επίσης η είναι επί συνάρτηση αφού αν , , ώστε . Τέλος η είναι ομομορφισμός. Πράγματι, αν , τότε
| (2.155) |
Άρα η είναι ομομορφισμός ομάδων και
| (2.156) |
Έστω , δηλαδή , μία πολλαπλασιαστική κυκλική ομάδα τάξης . Θεωρούμε την αντιστοιχία
| (2.157) |
Η είναι αμφιμονότιμη συνάρτηση. Πράγματι, έστω με (βλέπε Πρόταση 2.2.2, ). Είναι φανερό ότι η είναι επί συνάρτηση, αφού αν τότε . Τέλος η είναι ομομορφισμός. Πράγματι; αν , τότε
| (2.158) |
Επομένως η είναι ισομορφισμός και
| (2.159) |
Ασκήσεις
1. Να αποδείξετε ότι η συνάρτηση
| (2.160) |
όπου είναι πραγματικοί αριθμοί, είναι μονομορφισμός πολλαπλασιαστικών ομάδων.
2. Έστω . Να αποδείξετε ότι η συνάρτηση
| (2.161) |
είναι ισομορφισμός της πολλπαπλασιαστικής ομάδας με την προσθετική ομάδα . Ακόμη να αποδείξετε ότι η συνάρτηση
| (2.162) |
είναι επιμορφισμός, αλλά όχι ισομορφισμός πολλαπλασιαστικών ομάδων.
3. Να αποδείξετε ότι οι ομάδες και η δεν μπορεί να είναι ισόμορφες.
4. Έστω . Να αποδείξετε ότι η συνάρτηση
| (2.163) |
είναι επιμορφισμός προσθετικών ομάδων.
5. Έστω μία κυκλική ομάδα άπειρης τάξης. Να αποδείξετε ότι κάθε μη τετριμμένη υποομάδα της είναι ισόμορφη με την . Η πρόταση ισχύει για πεπερασμένες κυκλικές ομάδες;
6. Στο Παράδειγμα 1.2.8.1 δίνονται οι πίνακες Cayley ομάδων τάξης .
-
Να βρείτε ποιές από αυτές είναι κυκλικές ομάδες.
-
Να βρείτε τις μη ισόμορφες από τις τέσσερις αυτές ομάδες.
-
Ποιές από αυτές είναι ισόμορφες με την ;
7. Έστω ένας μονομορφισμός ομάδων. Να αποδείξετε ότι .
8. Δίνεται η συνάρτηση
| (2.164) |
όπου και είναι η πολλαπλασιαστική ομάδα του . Να αποδείξετε ότι η είναι επιμιρφισμός ομάδων και
9. το σύνολο των ριζών της εξίσωσης στο σύνολο των μιγαδικών αριθμών, δηλαδή η είναι το σύνολο των -ριζών της μονάδας.
-
.
Να αποδείξετε ότι η είναι υποομάδα της .
-
.
Η είναι κυκλική ομάδα.
-
.
Η συνάρτηση
(2.165) είναι επιμορφισμός της επί της .
10. Έστω μία ομάδα και , . Να αποδείξετε ότι η είναι αβελιανή αν και μόνον αν η είναι ενδομορφισμός της .
11. Να αποδείξετε ότι υπάρχουν πεπερασμένου μόνο πλήθους μη ισόμορφες ομάδες τάξης .
12. Έστω , δύο πεπερασμένα σύνολα τέτοια, ώστε . Να αποδείξετε ότι .
13. Για τις ομάδες και , με , να αποδείξετε ότι η
| (2.166) |
είναι επιμορφισμός ομάδων και να υπολογίσετε τον πυρήνα της.
14. Να υπολογίσετε τον πυρήνα των παρακάτω ομομορφισμών ομάδων:
-
.
,
-
.
.
15. Δίνεται ο ομομορφισμός πολλαπλασιαστικών ομάδων . Να αποδείξετε ότι
-
.
Αν με , τότε .
-
.
Αν με , τότε .
-
.
Αν ο είναι μονομορφισμός και , τότε .
16. Δίνεται μία κυκλική ομάδα και . Να αποδείξετε ότι, αν είναι ένα παράγον στοιχείο της , τότε το είναι επίσης ένα παράγον στοιχείο της .
17. Να αποδείξετε ότι
-
.
.
-
.
Έστω , να αποδείξετε ότι
(2.167) όπου .
18. Έστω μία ομάδα, για κάθε , ορίζουμε την αντιστοιχία
| (2.168) |
-
.
Να αποδείξετε ότι η είναι αυτομορφισμός της . Ο ονομάζεται εσωτερικός αυτομορφισμός (inner automorphism) της . Έστω
(2.169) -
.
Να αποδείξετε ότι . Η υποομάδα λέγεται ομάδα των εσωτερικών αυτομορφισμών της .
-
.
Να αποδείξετε ότι αν και μόνον αν η είναι αβελιανή ομάδα.
19. Να αποδείξετε ότι .