7.2 Μέθοδος των Lax–Wendroff
7.2.1 Μια μη ευσταθής μέθοδος
Στη συνέχεια, θα θεωρήσουμε ένα αριθμητικό σχήμα που να προσεγγίζει με μεγαλύτερη ακρίβεια τη , από τις δύο προηγούμενες μεθόδους upwind και downwind. Έτσι, αν στην (7.2) θεωρήσουμε για την προσέγγιση της την και για την την , τότε έχουμε για , και ,
| (7.17) |
όπου, αν , λόγω των (2.3) και (2.4),
| (7.18) |
Συνεπώς, ισχύει το ακόλουθο λήμμα.
Λήμμα 7.2.
Θεωρούμε, λοιπόν, την ακόλουθη μέθοδο για να κατασκευάσουμε προσεγγίσεις των τιμών ,
| (7.20) |
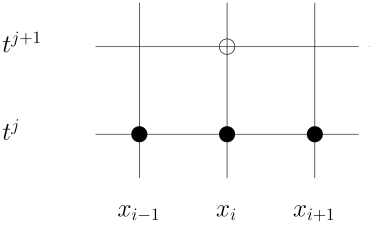
Ξεκινώντας από το χρονικό επίπεδο όπου γνωρίζουμε ότι , , και χρησιμοποιώντας την (7.20), μπορούμε να βρούμε με άμεσο τρόπο την προσέγγιση , , στο επόμενο χρονικό επίπεδο , όμως παρατηρούμε ότι δεν μπορούμε να υπολογίσουμε την . Επομένως, όπως και στη μέθοδο (7.11), για να βρούμε όλες τις τιμές στα επόμενα χρονικά επίπεδα , , χρειάζεται να γνωρίζουμε την , για . Έτσι, υποθέτουμε ότι στο πρόβλημα (7.1), η ακριβής λύση ικανοποιεί επιπλέον και τη συνοριακή συνθήκη , , οπότε θέτουμε , .
Συνεπώς, αν συμβολίσουμε τώρα , τότε η (7.20) μπορεί να γραφεί
| (7.21) | ||||||
Οπότε τώρα χρησιμοποιώντας την (7.21), βρίσκουμε με άμεσο τρόπο όλες τις τιμές στα επόμενα χρονικά επίπεδα , .
Εύκολα παρατηρούμε ότι χρησιμοποιώντας τη μέθοδο (7.21), η τιμή της προσέγγισης στο σημείο , εξαρτάται τελικά από τις τιμές στα σημεία , , , , , βλ. Σχήμα 7.9. Για να ικανοποείται τώρα η συνθήκη CFL αρκεί το διάστημα , το οποίο περιέχει τα σημεία του χωρίου υπολογιστικής εξάρτησης της μεθόδου, να περιέχει το , το οποίο ισχύει ανεξάρτητα από το πρόσημο της σταθεράς , αν . Επίσης, ακολουθώντας τα βήματα για τη μέλετη της ευστάθιας von Neumann για τις μεθόδους upwind και downwind, έχουμε ότι, αν και πάλι θέσουμε , με ,
Οπότε, εφαρμόζοντας την τριγωνομετρική ταυτότητα (5.18), παίρνουμε
Συνεπώς, , με , και
Επομένως, η μέθοδος (7.21) δεν είναι von Neumann ευσταθής, γιατί .
7.2.2 Μέθοδος Lax–Wendroff
Στη συνέχεια, θα κατασκευάσουμε μια νέα μέθοδο για την προσέγγιση της (7.1) η οποία θα χρησιμοποιεί τα ίδια σημεία του πλέγματος όπως η (7.21), θα είναι von Neumann ευσταθής και θα έχει και αυτή τοπικό σφάλμα το οποίο θα τείνει στο μηδέν, καθώς και τείνουν στο μηδέν. Θέτουμε, λοιπόν, για , ,
| (7.22) |
και θέλουμε να προσδιορίσουμε τα και , έτσι ώστε το τοπικό σφάλμα να είναι όσο το δυνατόν μικρότερο. Χρησιμοποιώντας το γεγονός ότι , και και αναπτύσσοντας σύμφωνα με το Θεώρημα Taylor, έχουμε
| (7.23) |
με
| (7.24) |
και όμοια
| (7.25) |
με
| (7.26) |
Αν αντικαταστήσουμε τις (7.23) και (7.25) στην (7.22), έχουμε
Επομένως
Στη συνέχεια, εξισώνοντας τους συντελεστές των στην παραπάνω εξίσωση με το μηδέν, προκύπτουν οι ακόλουθες σχέσεις
Επομένως, έχουμε , και . Συνεπώς, για αυτήν την επιλογή των και έχουμε
| (7.27) |
Οπότε, λόγω των (7.24) και (7.26), έχουμε ότι υπάρχει σταθερά ανεξάρτητη των και , τέτοια ώστε
Η μέθοδος που προκύπτει για την παραπάνω επιλογή των συντελεστών και ονομάζεται μέθοδος των Lax–Wendroff και για να μπορέσουμε να βρούμε την προσέγγιση σε κάθε χρονικό επίπεδο , , χρειάζεται, όπως και στην (7.21) να θεωρήσουμε γνωστή την ακριβή λύση για και . Έτσι, η μέθοδος Lax–Wendroff ορίζεται ως εξης
| (7.28) |
Εύκολα μπορούμε να δούμε ότι το χωρίο υπολογιστικής εξάρτησης για το είναι το ίδιο με τη μέθοδο (7.21) και εξαρτάται από τα σημεία , βλέπε Σχήμα 7.9. Επίσης για να ικανοποείται η συνθήκη CFL πρέπει το σημείο να περιέχεται στο διάστημα , το οποίο ισχύει ανεξάρτητα από το πρόσημο της σταθεράς , αν .
Παράδειγμα 7.4.
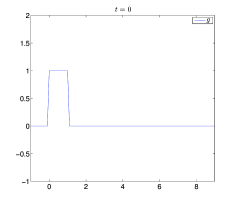
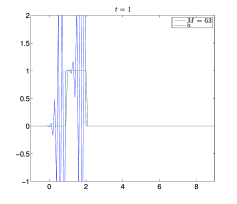
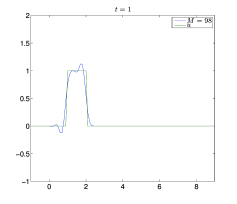
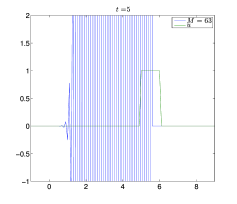
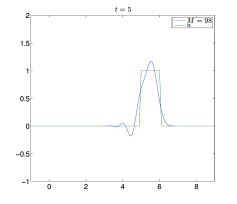
Θεωρούμε και πάλι το πρόβλημα των Παραδειγμάτων 7.1 και 7.2, στο διάστημα , με όπως στο Παράδειγμα 1.2, και . Επειδή γνωρίζουμε ότι , για , μπορούμε να θέσουμε , . Επίσης, διαμερίζουμε το σε σημεία, με και το σε , με . Στα Σχήματα 7.10 και 7.11 βλέπουμε την ακριβή λύση και τις προσεγγίσεις με τη μέθοδο των Lax–Wendroff (7.28) για . Παρατηρούμε ότι η προσεγγιστική λύση έχει παρόμοια συμπεριφορά όπως και αυτή της μεθόδου upwind στο Παράδειγμα 7.1. Έτσι αν , για , τότε το σφάλμα της προσεγγιστικής λύσης είναι μεγάλο, ενώ το μικρότερο σφάλμα προκύπτει αν και είναι πιο κοντά στη μονάδα.
 |
 |
 |
 |
 |
 |
 |
7.2.3 Ευστάθεια και σύγκλιση
Για τη μελέτη της ευστάθειας von Neumann για τη μέθοδο των Lax–Wendroff, θα θεωρήσουμε και πάλι ότι η προσεγγιστική λύση είναι της μορφής , , οπότε σύμφωνα με την (7.28), έχουμε
Χρησιμοποιώντας τώρα τις (5.23) και (5.18), παίρνουμε
Συνεπώς, , με . Οπότε
Χρησιμοποιώντας τώρα την τριγωνομετρική ιδιότητα , η παραπάνω σχέση γίνεται
Είναι προφανές ότι, αν , τότε , και, άρα, η μέθοδος Lax–Wendroff είναι von Neumann ευσταθής, αν .
Για να δείξουμε τη σύγκλιση της μεθόδου Lax–Wendroff χρειάζεται να εφαρμόσουμε παρόμοια επιχειρήματα όπως αυτά της μεθόδου ενέργειας στην Παράγραφο 3.4, βλ. παραδείγματος χάριν (Larsson and V. Thomée, (2009), Παράγραφος 12.3), η απόδειξη του οποίου είναι πολύπλοκη και ξεφεύγει από τους σκοπούς αυτών των σημειώσεων. Διατυπώνουμε, επομένως, το επόμενο θεώρημα χωρίς απόδειξη.
Θεώρημα 7.3.
Στο ακόλουθο παράδειγμα βλέπουμε και πειραματικά ότι το σφάλμα με τη μέθοδο Lax–Wendroff έχει μεγαλύτερη τάξη προσέγγισης ως προς και από το σφάλμα της μεθόδου upwind ή downwind.
Παράδειγμα 7.5.
Βασική υπόθεση στα θεωρήματα σύγκλισης για τις μεθόδους που μελετήσαμε σε αυτό το κεφάλαιο είναι ότι η ακριβής λύση , και κατά επέκταση η συνάρτηση της αρχικής συνθήκης , είναι αρκετά ομάλη. Είναι προφανές ότι η που θεωρήσαμε στα προηγούμενα παραδείγματα δεν είναι ομαλή συνάρτηση, για αυτό τον λόγο τώρα θεωρούμε το πρόβλημα (7.13) στο διάστημα , με
Επειδή η σταθερά του (7.13) είναι θετική για να ικανοποιείται η συνθήκη CFL θα χρησιμοποιήσουμε τις μεθόδους upwind και Lax–Wendroff. Θεωρούμε τώρα διαμερίσεις του με , , , , , , και του , με αντίστοιχο βήμα , τέτοιο ώστε . Θέτουμε , με το σφάλμα της προσεγγιστικής λύσης που προκύπτει με τη μεθόδο upwind και με ανάλογο τρόπο ορίζουμε το σφάλμα με τη μέθοδο των Lax–Wendroff. Στον πίνακα 7.1 βλέπουμε τα σφάλματα αυτών των δύο μεθόδων και την προσεγγιστική τάξη ακριβείας .
| Upwind | Lax–Wendroff | |||
|---|---|---|---|---|
| 0.05 | 0.0483 | 0.01965 | ||
| 0.025 | 0.0325 | 0.574 | 0.00960 | 1.034 |
| 0.0125 | 0.0208 | 0.642 | 0.00413 | 1.216 |
| 0.0063 | 0.0127 | 0.713 | 0.00151 | 1.456 |
| 0.0031 | 0.0073 | 0.785 | 0.00045 | 1.743 |
| 0.0016 | 0.0040 | 0.852 | 0.00012 | 1.848 |
| 0.0008 | 0.0021 | 0.906 | 0.00003 | 1.992 |