7 Στοχαστικά Συστήματα – Μέθοδοι Monte Carlo 7.5 Παράδειγμα – Μοριακό Μοντέλο Σκληρών Σφαιρών A Βασικά μαθηματικά εργαλεία

7.6 Μελέτη

7.6.1 Ασκήσεις

Άσκηση 7.1.

Οι «βελόνες του Buffon»
Θεωρήστε ένα χώρο με παράλληλες ξύλινες πλάκες, με ακριβώς το ίδιο πάχος, και πετάμε σε αυτόν μια βελόνα. Το πάχος κάθε πλάκας είναι t και το μήκος κάθε βελόνας $\ell$ . Θεωρούμε ότι ρίχνουμε τυχαία βελόνες μέσα στο χώρο.

Α) Βρείτε τη πιθανότητα, $P$ , η βελόνα να διασταυρώνει μια γραμμή (την ένωση) μεταξύ δύο πλακών για κάθε περίπτωση.

Β) Δείξτε ότι αν υποθέσουμε ότι το μήκος κάθε βελόνας είναι μικρότερο του πάχους των πλακών, δηλαδή $\ell<t$ , τότε η ζητούμενη πιθανότητα είναι:

P=\frac{2\ell}{\pi t}.

[Υπόδειξη: Ορίστε δύο ασυσχέτιστες τ.μ. (α) την απόσταση του κέντρου της βελόνας από την κοντινότερη γραμμή, $X$ , και (β) τη γωνία μεταξύ της βελόνας και των γραμμών, $\theta$ , (παράλληλη γραμμή που διέρχεται από την αρχή της βελόνας). Κατόπιν υπολογίστε την πιθανότητα ως ολοκλήρωμα σε όλες τις πιθανές τιμές των $X,\theta$ .

Άσκηση 7.2.

Αλγόριθμος Box – Muller
Υλοποιήστε τον αλγόριθμο Box – Muller όπως παρουσιάστηκε παραπάνω. Μελετήστε την κατανομή των τυχαίων αριθμών που προκύπτει.

Άσκηση 7.3.

Γεννήτρια Τυχαίων Αριθμών
Στόχος της άσκησης αυτής είναι η εξέταση της αποδοτικότητας γεννητριών τυχαίων αριθμών. Για τα παρακάτω προγράμματα μπορείτε να χρησιμοποιήσετε οποιαδήποτε γλώσσα προγραμματισμού προτιμάτε (π.χ. MATLAB, C++, Fortran90). Α) Θεωρήστε τον συμβατική αλγόριθμο δημιουργίας ακολουθίας τυχαίων αριθμών (congruential generator), $X=[X_{i}]\,(i=1,2,\ldots,n)$ :

Y_{i}=D(x)=(aY_{i-1}+b)\mod(M),\qquad X_{i}=\frac{Y_{i}}{M}

όπου $a, b, M$ είναι σταθερές (φυσικοί αριθμοί). Υπολογίστε:

(1)

Αν, για δεδομένο n, η ακολουθία $X$ υπακούει την ομοιόμορφη κατανομή στο $[0,1]$ . Υπολογίστε την πιθανότητα κάνοντας το ιστόγραμμα της $X$ .
(2)

Μελετήστε αν υπάρχει συσχέτιση μεταξύ διαδοχικών τυχαίων αριθμών κάνοντας το διάγραμμα $X_{2k-1}$ , vs. $X_{2k}$ .

Θεωρήστε διαφορετικές τιμές για τις σταθερές (π.χ. $a=453,b=10,M=213$ ) και διαφορετικές τιμές του n.

B) Όπως έχουμε αναφέρει υπάρχουν καλύτεροι αλγόριθμοι δημιουργίας τυχαίων αριθμών. Θεωρείστε την προεπιλεγμένη γεννήτρια τυχαίων αριθμών της γλώσσας που χρησιμοποιείται (π.χ. MATLAB: συνάρτηση rand, Mersenne Twister algorithm). Περιγράψτε τον παραπάνω αλγόριθμο Mersenne Twister (http://www.math.sci.hiroshima-u.ac.jp/ m-mat/MT/emt.html).

Γ) Επαναλάβετε τα παραπάνω βήματα για την προεπιλεγμένη γεννήτρια τυχαίων αριθμών της γλώσσας που χρησιμοποιείται (π.χ. MATLAB: συνάρτηση rand, Mersenne Twister algorithm).

Άσκηση 7.4.

Υπολογισμός του Αριθμού $\pi$ – «Πείραμα της Βροχής»
Θεωρήστε τον αλγόριθμο υπολογισμού του αριθμού $\pi$ που συζητήσαμε στην τάξη και ο οποίος βασίζεται στον υπολογισμό του εμβαδόν ενός κύκλου και του τετραγώνου με το οποίο τον περικλείουμε (raindrop experiment).

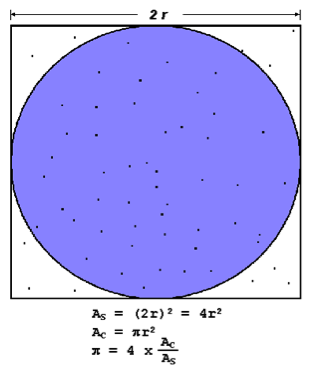
Σχήμα 7.8: Υπολογισμός του Αριθμού $\pi$ – «Πείραμα της Βροχής»

Φτιάξτε ένα αλγόριθμο υπολογισμού του $\pi$ χρησιμοποιώντας μια κατάλληλη γεννήτρια τυχαίων αριθμών. Έστω n ο αριθμός των τυχαίων σημείων μέσα στο τετράγωνο. Βρείτε και γράψτε σε μια αναφορά τα ακόλουθα:

Α)

Περιγράψτε λεπτομερώς τον αλγόριθμο που χρησιμοποιείτε.
Β)

Υπολογίστε τον αριθμό $\pi$ για $n=1000,10000,1000000$ . Για καλύτερη ακρίβεια τρέξτε το πρόγραμμα 10 φορές για κάθε n και υπολογίστε τη μέση τιμή του $\pi$ . Φτιάξτε ένα διάγραμμα με όλες τις τιμές (εκτιμήσεις) του $\pi$ .
Γ)

Υπολογίστε το σφάλμα των μετρήσεων χρησιμοποιώντας την ακριβή τιμή του αριθμού $\pi$ ( $\pi=3.141592653589793$ ). Κάντε το διάγραμμα του σφάλματος της μέτρησης ως προς τον αριθμό των τυχαίων σημείων $n$ . Εκτιμήστε πόσο μεγάλο πρέπει να είναι το n για ακρίβεια υπολογισμού του $\pi$ ίση με: 3, 5, 7 σημαντικών ψηφίων.

Άσκηση 7.5.

Αλγόριθμος Metropolis
Στόχος της άσκησης αυτής είναι η μελέτη αλγορίθμων Monte Carlo Μαρκοβιανών Αλυσίδων (MCMC) τύπου Metropolis τυχαίου περιπάτου (random walk). Έστω τυχαία μεταβλητή (τ.μ.) $x$ , η Μαρκοβιανή αλυσίδα της οποίας δίνεται από τον κανόνα μετάβασης:

y_{i}=x^{(t)}+A\epsilon_{t}

όπου $x(t)$ είναι η τιμή της τ.μ. στην επανάληψη $t$ και $y_{t}$ η προτεινόμενη τιμή στην επόμενη επανάληψη. $A$ είναι μια σταθερά και $\epsilon t$ μια τυχαία μεταβλητή η οποία έρχεται μέσα από μια συμμετρική κατανομή $f()$ .

H Μαρκοβιανή αλυσίδα, που σχετίζεται με την κατανομή $f$ , είναι τυχαίος περίπατος στη μεταβλητή $\epsilon$ και στην μεταβλητή $x$ . Δημιουργήστε γενικό αλγόριθμο Metropolis MC της μορφής:

•

Δεδομένου $x(t)$ δημιουργήστε $y_{t}\sim f(|y-x(t)|)$ .
•

$x^{(t+1)}=\begin{cases}y_{t},\quad\hbox{με πιθανότητα}\quad\rho\left(x^{(t)},y% _{t}\right)=\min\left\{1,\frac{f\left(y_{t}\right)}{f\left(x^{(}t)\right)}% \right\}\\ x^{(t)},\quad\hbox{αλλιώς}.\end{cases}$

Χρησιμοποιήστε σαν $f()$ :

(α)

Ομοιόμορφη κατανομή στο διάστημα $[-\delta,\delta]$ ,
(β)

Κανονική κατανομή $N(0,1)$ στο διάστημα $[-\delta,\delta]$ .
(γ)

Εκθετική κατανομή ${\rm Exp}()$ , στο διάστημα $[-\delta,\delta]$ , αφού πρώτα την κανονικοποίησετε.

Σε όλες τις παραπάνω περιπτώσεις $\delta$ είναι μια σταθερά.

1) Περιγράψτε τον αλγόριθμο Metropolis. Βρείτε την πιθανότητα αποδοχής συναρτήσει της σταθεράς $A$ .

2) Τρέξτε τον αλγόριθμο για διαφορετικές τιμές των σταθερών $\delta$ και $A$ : π.χ. $(\delta=0.5,A=4),\,(\delta=1.0,A=4),\,(\delta=0.5,A=2),\,(\delta=0.5,A=10)$ , για τις τρεις διαφορετικές κατανομές. Υπολογίστε σε κάθε περίπτωση την κατανομή πιθανότητας της (τ.μ.) $x$ σε μορφή ιστογράμματος.

3) Τρέξτε τον αλγόριθμο για διαφορετικές τιμές του μεγέθους της αλυσίδας (αριθμός των επαναλήψεων) $n$ , π.χ. $n=1000,10000,100000$ . Υπολογίστε σε κάθε περίπτωση την κατανομή πιθανότητας της (τ.μ.) $x$ σε μορφή ιστογράμματος.

4) Υπολογίστε τη μέση τιμή και τη διακύμανση για κάθε μια από τις παραπάνω περιπτώσεις των ερωτημάτων (2) και (3). Εξετάστε επίσης τη σύγκλιση της μέσης τιμής κάνοντας διαγράμματα μέσης τιμής, $\mu(i)$ , συνάρτηση της επανάληψης $i,\,i=1,2,\ldots,n$ .

7.6.2 Εργασίες

Εργασία 7.1.

Ταχύτητα Σύγκλισης MCMC Αλγορίθμων
Μια βασική παράμετρος σε κάθε MC αλγόριθμο είναι η ταχύτητα σύγκλισης, δηλαδή το πόσο «γρήγορα» δειγματοληπτεί από τη σωστή κατανομή. Αυτό είναι ιδιαίτερα σημαντικό στους αλγορίθμους τύπου MCMC όπως Metropolis – Hastings. Μελετήστε θεωρητικά την ταχύτητα σύγκλισης των αλγορίθμων MCMC. Κατόπιν εξετάστε τις θεωρητικές προβλέψεις εφαρμόζοντας τον αλγόριθμο σε ένα τυπικό παράδειγμα.

Βιβλιογραφία: [30, 23].

Εργασία 7.2.

Μοντέλο Lennard – Jones
Ένα κατάλληλο μοντέλο για την περιγραφή μοριακών συστημάτων, πιο ακριβές από το μοντέλο σκληρών σφαιρών, είναι το μοντέλο Lennard – Jones (LJ) (Δες Κεφάλαιο 2). Αναπτύξτε αλγόριθμο Metropolis Monte Carlo για τη μελέτη $N$ μορίων / σωματιδίων μέσα σε ένα κουτί τα οποία αλληλεπιδρούν με δυναμικό LJ. Μελετήστε τη συμπεριφορά των σωματιδίων και υπολογίστε την ενέργεια του συστήματος συναρτήσει του αριθμού των κινήσεων Monte Carlo.

Βιβλιογραφία: [21].

Εργασία 7.3.

Μοντέλο Ising
Ένα κατάλληλο μοντέλο για την περιγραφή στερεών συστημάτων είναι τα μοντέλα πλέγματος τύπου Ising. Αναπτύξτε αλγόριθμο Metropolis Monte Carlo για τη μελέτη $N$ μορίων / σωματιδίων τα οποία αλληλεπιδρούν με δυναμικό Ising.

Βιβλιογραφία: [21].

Εργασία 7.4.

Δειγματοληψία Gibbs
Μια επέκταση των αλγορίθμων MCMC τύπου Metropolis – Hastings δίνεται μέσω τροποποιημένης δειγματοληψίας Gibbs (Gibbs Sampler ή Multi-stage Gibbs sampler). Αναπτύξτε αλγόριθμο δειγματοληψίας Gibbs Monte Carlo και δείτε τις διαφορές του σε σχέση με τον τυπικό αλγόριθμο Metropolis – Hastings.

Βιβλιογραφία: [30].

7.6.3 Αλγόριθμοι / Κώδικες

Κώδικας MATLAB για τη δημιουργία τυχαίων αριθμών


% =========================================================================
%  ------  Random Number Generators (RNGs)-------------
%
% This is an m-file that examines basic Random Number Generators (RNGs)
% The following cases are considered:
%
% (a) Uniform distribution in (0,1) using the Congruential Generator
% (b) Uniform distribution in (0,1) using the Mersenne Twister algorithm
% (c) Normal distribution in (0,1) using the default algorithm in Matlab
% (a) Uniform distribution in (a,b).
%
% =========================================================================

% Clears history and command window
close all; clear all;

% number of points (random numbers) to be created
n = 1000;
n = 100000;

% ---------- Uniform in [0,1] ----------------------
% -- Congruential Generator
%1o set parametwn
a=1229;
b=1;
y0=3;
M=2^11;
%2o set parametrwn
% a=65539;
% b=0;
% y0=1;
% M=2^31;

y=zeros(n,1);

for i=1:n
y(i)=mod(a*y0+b,M);
y0=y(i);
end
% x omoiomorfh sto [0 1]
x=y/M;

% plots
%--tyxaioi arithmoi
figure(1)
hold on;
title('Values of X')
plot(x,'.-g')
xlabel('Iterations');
ylabel('Random numbers');
hold off;
%--istogramma pithanothta
figure(2)
hist(x,100);
title('Histogram of X')
ylabel('Frequency')
xlabel('Numbers')
%-- sysxetish
figure(3)
plot(y(1:end-2),y(2:end-1),'.b');
title('Sysxetish metaxy 2 diadoxikwn arithmwn ths Y')
xlabel('x_{2k}');
ylabel('x_{2k-1}');


% -- Mersenne Twister (defalut, "rand" function, in Matlab)
y = rand(1,n);
figure(4);
hist(y,100);
title('"n" Random Numbers: Uniform');
%-- sysxetish
figure(5)
plot(y(1:end-2),y(2:end-1),'.b');
title('Sysxetish metaxy 2 diadoxikwn arithmwn ths Y')
xlabel('x_{2k}');
ylabel('x_{2k-1}');


% ---------- Normal [0,1] ----------------------
y1 = randn(1,n);
figure(6);
hist(y1,200);
title('"n" Random Numbers: Normal');


% ---------- Uniform in [a, b] ----------------------
% The following code demonstrates a method for generating
% random numbers between (a) and (b).
% The round function is used to round the number to the closest
% whole number.
a = 0;
b = 20;
y2 = round(a + (b-a) * rand(1,n));
figure(7);
hist(y2);
title('"n" Random Numbers: Normal between "a" and "b"');

Κώδικας MATLAB για το «Πείραμα της Βροχής»


% =========================================================================
%  ------  Raindrop Experiment - Computation of Number pi -------------
%
% This is an m-file that performs the raindrop experiment in order to
% compute the number pi.
%
% =========================================================================

% Clears history and command window
close all; clear all;

% number of points to be created
m=10000;
% m=10;
% creation of
x=rand(1,m);
y=rand(size(x));
%x(5)=0.5;
%y(5)=0;
theta=linspace(0,2*pi);
xc=0.5*cos(theta)+0.5;
yc=0.5*sin(theta)+0.5;
in = inpolygon(x,y,xc,yc);
s=sum(in);
P=4*s/m;

plot(xc,yc,x(in),y(in),'.b',x(~in),y(~in),'.r')
%h=title({['pi approximation = ',num2str(P)]});
xlabel(['m =',num2str(m)])
axis equal
disp([P,abs(P-pi)])
disp(['m = ',num2str(m)])

Πρότυπο (template) κώδικα MATLAB ανάπτυξης Αλγορίθμου Metropolis


% =========================================================================
%  ------  Metropolis Monte Carlo -------------
%
% This is an m-file that can be used as a template to develop Metropolis
% Monte Carlo algorithm for a system.
%
% =========================================================================

% Clears history and command window
close all; clear all;

% Parameters, Initialization of variables
n = ...;
delta = ...;
mu = ...;
sigma = ...;
x = zeros(1,n);
x(1)= ...;

% Main loop
for i=2:n

% Step 1: create proposal from a transition rule
  epsilon = ...;
  y = ...;

% Step 2: calculate r = min[1,pi(y)/pi(x)]
  r = ...;
  r = min(r,1);

% Step 3: accept or reject proposal
  u = rand(1);
  if u <= r % accept y
    x(i) = ...;
  else % reject y
    x(i) = ...;
  end
end

% Plot data
figure(1)
hist(x);
xlabel('this is a test: change label');
ylabel('this is a test: change label');