7 Στοχαστικά Συστήματα – Μέθοδοι Monte Carlo 7.4 Αλγόριθμοι Monte Carlo Μαρκοβιανών Αλυσίδων 7.6 Μελέτη

7.5 Παράδειγμα – Μοριακό Μοντέλο Σκληρών Σφαιρών

Εδώ παρουσιάζουμε ένα πρώτο παράδειγμα εφαρμογής αλγορίθμων Monte Caro βασισμένων σε Μαρκοβιανές Αλυσίδες, και πιο συγκεκριμένα του αλγορίθμου Metropolis Monte Carlo.

Έστω $N$ σφαιρικά σωματίδια (π.χ. άτομα ή μόρια), με συντεταγμένες

\bm{r}=(r_{1},r_{2},\ldots,r_{N})

σε ένα κουτί. Θεωρούμε ότι τα σωματίδια αλληλεπιδρούν ανά δύο, με ένα δυναμικό ζεύγους (pair potential) αλληλεπίδρασης της μορφής:

U(\bm{r})=\sum_{i=1,\,j>i}^{N}U(r_{ij}),\qquad U(r_{ij})=\begin{cases}\infty,% \qquad\hbox{αν}\quad r_{ij}\leq d\\ 0,\qquad\hbox{αν}\quad r_{ij}>d\end{cases}

(7.21)

όπου $r_{ij}$ είναι το μέτρο της απόστασης μεταξύ δύο σωματιδίων $i, j$ και $d$ η διάμετρος κάθε σωματιδίου.

Αν εξετάσουμε το πρόβλημα σε 3 διαστάσεις (η πιο γενική μορφή, αλλά επίσης το πρόβλημα μπορεί να μελετηθεί σε 2 ή ακόμη και 1 διάσταση), με $x_{i},y_{i}$ , και $z_{i}$ , αντίστοιχα τις $x, y, z$ συντεταγμένες, στο Καρτεσιανό επίπεδο, του μορίου i τότε η απόσταση μεταξύ δύο σωματιδίων $i$ και $j$ είναι:

t_{ij}=\sqrt{(x_{i}-x_{j})^{2}+(y_{i}-y_{j})^{2}+(z_{i}-z_{j})^{2}}.

Πρακτικά, το ότι η ενέργεια είναι άπειρη για αποστάσεις μικρότερες ή ίσες του $d$ σημαίνει ότι τα σωματίδια δεν μπορούν να βρεθούν σε αποστάσεις μικρότερες ή ίσες με $d$ , ενώ μηδενική ενέργεια για αποστάσεις μεγαλυτερες του $d$ , σημαίνει ότι σε αυτές τις αποστάσεις τα σωματίδια δεν αλληλεπιδρούν. Για το λόγο αυτό το παραπάνω μοντέλο ονομάζεται μοντέλο «σκληρών σφαιρών» (hard spheres model).

Παρατήρηση 7.9.

Αν θεωρήσουμε ότι τα παραπάνω σωματίδια αντιπροσωπεύουν ένα μοριακό σύστημα στο κανονικό στατιστικό σύνολο NVT (σταθερός αριθμός σωματιδίων $N$ , όγκου του συστήματος $V$ και θερμοκρασίας $Τ$ ) τότε η κατανομή την οποία υπακούουν είναι η κατανομή Boltzmann (δες Εξ. (7.11)):

\pi(\bm{r})=\frac{\exp⁡[-\beta U(\bm{r})]}{\iiint\exp⁡[-\beta U(\bm{r})]d\bm{r% }}=\frac{1}{Z}\,\exp⁡[-\beta U(\bm{r})]

όπου $\beta$ είναι η αντίστροφη θερμική ενέργεια, $\beta=1/(k_{B}T)$ , όπου $k_{B}$ είναι η σταθερά Boltzmann και $T$ η θερμοκρασία του συστήματος.

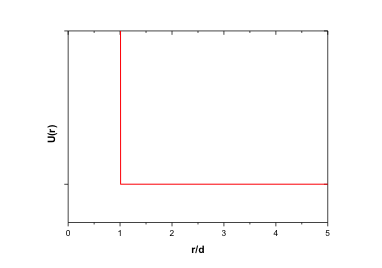
Σχήμα 7.7: Δυναμικό αλληλεπίδρασης μοντέλου σκληρών σφαιρών.

Στο Σχήμα 7.7 φαίνεται η μορφή του δυναμικού σκληρών σφαιρών. Προσέξτε ότι το παραπάνω δυναμικό καταρχήν δεν είναι ένα ρεαλιστικό δυναμικό για συγκεκριμένα μοριακά συστήματα. Σε μακροσκοπικό επίπεδο θα λέγαμε ότι τα σωματίδια συμπεριφέρονται σαν «μπάλες μπιλιάρδου».

Αντίθετα υπάρχουν πιο ρεαλιστικά δυναμικά (π.χ. δυναμικό Lennard – Jones) τα οποία εμφανίζουν πιο ρεαλιστική περιοχή άπωσης και έλξης. Ωστόσο το δυναμικό σκληρών σφαιρών είναι μια πολύ καλή πρώτη προσέγγιση για μεγάλο εύρος μοριακών συστημάτων, όπως αερίων, απλών μορίων, κολλοειδών, κλπ.

Ο αλγόριθμος Metropolis Monte Carlo για το παραπάνω μοντέλο σωματιδίων τύπου σκληρών σφαιρών αποτελείται από τα παρακάτω βήματα:

•

Βήμα 1: Έστω ότι τα σωματίδια βρίσκονται σε θέσεις $r$ . Τυχαία επιλογή ενός σωματιδίου, π.χ. το σωματίδιο $i$ με συντεταγμένες $x_{i}$ , $y_{i}$ , και $z_{i}$ .
•

Βήμα 2: (Κανόνας Μετάβασης) Προτεινόμενη νέα θέση μέσω τυχαίας μετατόπισης της θέσης του σωματιδίου σε κάθε διεύθυνση, δηλαδή:

$r_{i}^{\rm temp}=r_{i}+\Delta r,\qquad\hbox{ή}\qquad(x_{i}^{\rm temp},y_{i}^{% \rm temp},z_{i}^{\rm temp})=(x_{i}+\Delta x,y_{i}+\Delta y,z_{i}+\Delta z)$

όπου οι ποσότητες $\Delta x,\Delta y$ και $\Delta z$ είναι τυχαίες μεταβλητές από μια συγκεκριμένη κατανομή, π.χ. την τυπική κανονική, δηλαδή $\Delta x\sim N(0,1),\,\Delta y\sim N(0,1),\,\Delta z\sim N(0,1)$ .
•

Βήμα 3: Κατόπιν υπολογίζουμε την ποσότητα:

$\exp[-\beta\Delta U]=\exp\left[-\beta\left(U(r^{\rm temp})-U(r)\right)\right]$
•

Βήμα 4: Αποδοχή της νέας θέσης για το σωματίδιο $i$ , με πιθανότητα $\Delta U$ , δηλαδή δημιουργία τυχαίου αριθμού $u$ , από ομοιόμορφη κατανομή στο διάστημα $(0,1),\;u\sim U(0,1)$ και:

$r_{i}^{\rm new}=\begin{cases}\bm{r}_{i}^{\rm temp},\qquad\hbox{αν}\quad u\leq% \exp[-\Delta U]\\ \bm{r}_{i},\qquad\hbox{αν}\quad u>\exp[-\Delta U]\end{cases}$

Παρατήρηση 7.10.

Προσέξτε ότι η παραπάνω ποσότητα $\Delta U$ , στο μοντέλο των σκληρών σφαιρών, είναι $\infty$ ή $0$ . Συνεπώς πρακτικά το βήμα 4 δεν χρειάζεται καθώς η προτεινόμενη μετάβαση είναι αποδεκτή κάθε φορά που $\Delta U=0$ και μη αποδεκτή αν $\Delta U=\infty$ .

Με τον παραπάνω αλγόριθμο μπορούμε να δημιουργήσουμε μια Μαρκοβιανή αλυσίδα Τ.Μ. των θέσεων των σωματιδίων $\bm{r}$ , η οποία, σε μεγάλους χρόνους, υπακούει την επιθυμητή κατανομή Boltzmann. Κατόπιν οι τιμές της Μαρκοβιανής αλυσίδας μπορούν να χρησιμοποιηθούν για να υπολογίσουν αναμενόμενες (μέσες) τιμές για διάφορες ποσότητες – συναρτήσεις των $\bm{r}$ , όπως για παράδειγμα την ενέργεια, την πίεση ως συνάρτηση τη θερμοκρασίας $T$ .