6.1 Συνεχή Μοντέλα Αλληλεπιδρώντων Πληθυσμών
Όπως αναφέρθηκε στο προηγούμενο κεφάλαιο τα πληθυσμιακά μοντέλα ενός είδους βασίζονται στην υπόθεση ότι δεν υπάρχει κάποιο άλλο είδος το οποίο να επηρεάζει τον πληθυσμό του υπό εξέταση είδους. Σε πολλές περιπτώσεις όμως έχουμε ένα οικοσύστημα στο οποίο δύο ή περισσότερα είδη αλληλεπιδρούν ισχυρά και ο πληθυσμός τους δεν μπορεί να περιγραφεί ανεξάρτητα αλλά θα πρέπει να ληφθούν υπόψη οι πληθυσμοί όλων των ειδών. Χαρακτηριστικό παράδειγμα είναι ένα περιβάλλον (π.χ. δάσος) στο οποίο συνυπάρχουν δύο είδη από το οποία το ένα τρώει το άλλο (π.χ. λαγός – αλεπού) [26]. Μαθηματικά αυτό απαιτεί πεπλεγμένες εξισώσεις των μεταβλητών των πληθυσμών.
Η απλούστερη περίπτωση αλληλεπιδρώντων πληθυσμών αφορά τη μελέτη οικοσυστήματος στο οποίο δύο είδη αλληλεπιδρούν σε μεγάλο βαθμό. Υπάρχουν διαφορετικοί πιθανοί τύποι αλληλεπιδράσεων, οι κυριότεροι εκ των οποίων είναι οι εξής:
-
1.
Θηρευτής–Θήραμα (Predator-Pray): Αν το ένα είδος τρέφεται με το άλλο, ο πληθυσμός του ενός (θηράματος) μειώνεται και του άλλου (θηρευτή) αυξάνεται. Χαρακτηριστικό παράδειγμα: λαγός – αλεπού σε ένα δάσος.
-
2.
Ανταγωνισμός (Competition): Τα δύο είδη ανταγωνίζονται μεταξύ τους για κάποια κοινή τροφή στο οικοσύστημα. Σε αυτή την περίπτωση ο πληθυσμός και των δύο ειδών μειώνεται λόγω ανταγωνισμού. Χαρακτηριστικό παράδειγμα: δύο είδη πουλιών που ανταγωνίζονται για το ίδιο φαγητό.
-
3.
Συμβίωση (Mutualism ή Symbiosis): Τα δύο είδη βρίσκονται σε αρμονική συμβίωση καθώς το ένα «βοηθάει» το άλλο. Ο πληθυσμός και των δύο ειδών αυξάνει. Χαρακτηριστικό παράδειγμα: έντομα (π.χ. μέλισσες) – λουλούδια, ή πουλιά – ιπποπόταμος, που βρίσκονται σε αρμονική συνεργασία.
Σύντομο πρόβλημα 6.1.
Μπορείτε να προτείνετε περισσότερα παραδείγματα από κάθε παραπάνω τύπο οικοσυστήματος;
Παρακάτω θα παρουσιάσουμε διακριτά και συνεχή μοντέλα για κάθε μία από τις παραπάνω περιπτώσεις. Αρχικά θα δούμε μοντέλα τύπου θηρευτή-θηράματος και πιο συγκεκριμένα το μοντέλο Lotka-Volterra. Θα μελετήσουμε λεπτομερώς την μορφή, τα σημεία ισορροπίας και θα κάνουμε ανάλυση ευστάθειας του μοντέλου, χρησιμοποιώντας τα εργαλεία που είδαμε και στην ανάλυση των δυναμικών συστημάτων, στο Κεφάλαιο 3. Επίσης, θα συζητήσουμε και τη διακριτή μορφή του μοντέλου. Κατόπιν θα δούμε πιο συνοπτικά συνεχή και διακριτά μοντέλα ανταγωνισμού και συμβίωσης. Η λεπτομερής μελέτη (π.χ. ανάλυση ευστάθειας) αυτών των μοντέλων προτείνεται ως άσκηση για τον αναγνώστη. Περισσότερες πληροφορίες για κάθε μοντέλο μπορούν να βρεθούν σε πιο εξειδικευμένα συγγράμματα Μαθηματικής Βιολογίας. [1, 7, 32, 33, 5].
6.1.1 Μοντέλα Τύπου Θηράματος–Θηρευτή: Lotka–Volterra
Το πιο απλό μοντέλο θηράματος–θηρευτή (prey – predator), αλλά και συγχρόνως ίσως το πιο «διάσημο» μοντέλο Μαθηματικής Βιολογίας, είναι το μοντέλο Lotka-Volterra, το οποίο αναπτύχθηκε από τον Volterra το 1926 [Volterra, V., “Variazioni e fluttuazioni del numero d’individui in specie animali conviventi”, Mem. Acad. Lincei Roma, 2, 31–113, (1926), για να εξηγήσει τους περιοδικά ταλαντωμένους πληθυσμούς δύο ειδών ψαριών στην Αδριατική. Βασικές υποθέσεις του μοντέλου αυτού είναι ότι: (α) ο θηρευτής δεν μπορεί να τραφεί παρά μόνο με το θήραμα, ενώ (β) για το θήραμα υπάρχει «απεριόριστη» τροφή στο περιβάλλον. Αρχικά θα μελετήσουμε τη συνεχή και κατόπιν τη διακριτή του μορφή. [26, 37]
Έστω δύο είδη ψαριών από τα οποία το ένα τρέφεται με το άλλο και, οι πληθυσμοί των δύο ειδών περιγράφονται από συνεχείς μεταβλητές ως προς το χρόνο
-
•
: ο πληθυσμός του θηράματος (prey), και
-
•
: ο πληθυσμός του θηρευτή (predator), σε χρόνο .
Στόχος μας είναι η δημιουργία κατάλληλων μαθηματικών σχέσεων (στην περίπτωσή μας συνήθων διαφορικών εξισώσεων), οι οποίες περιγράφουν τη χρονική εξέλιξη των δύο πληθυσμών. Ξεκινάμε με συγκεκριμένα (βιολογικές) υποθέσεις. Θεωρούμε ότι:
-
1.
Ο πληθυσμός του θηράματος, απουσία του θηρευτή μεγαλώνει εκθετικά. Αυτό σημαίνει ότι στο ρυθμό μεταβολής (παράγωγος) του πληθυσμού του θηράματος θα υπάρχει θετικός όρος ().
-
2.
Αντίστοιχα ο πληθυσμός του θηρευτή, απουσία του θηρευτή μειώνεται εκθετικά. Αυτό σημαίνει ότι στο ρυθμό μεταβολής (παράγωγος) του πληθυσμού του θηρευτή θα υπάρχει αρνητικός όρος ().
-
3.
Η μείωση του πληθυσμού του θηράματος λόγω του θηρευτή είναι ανάλογη των «επαφών» θηράματος-θηρευτή, δηλαδή και μάλιστα είναι γραμμικής μορφής ως προς το γινόμενο . Δηλαδή στο ρυθμό μεταβολής του πληθυσμού του θηράματος υπάρχει αρνητικός όρος ().
-
4.
Αντίστοιχα η αύξηση του πληθυσμού του θηρευτή λόγω του θηράματος είναι ανάλογη των «επαφών» θηράματος-θηρευτή, δηλαδή και μάλιστα είναι γραμμικής μορφής ως προς το γινόμενο . Δηλαδή στο ρυθμό μεταβολής του πληθυσμού του θηράματος υπάρχει θετικός όρος ().
Στους παραπάνω όρους οι είναι θετικές σταθερές. Τελικά το συνεχές μοντέλο Lotka-Volterra περιγράφετε ως ένα σύστημα δύο (συνήθων) διαφορικών εξισώσεων:
| (6.1) |
Θα πρέπει εδώ να σημειώσουμε ότι αν και το παραπάνω μοντέλο (σύστημα εξισώσεων) εμφανίστηκε όπως αναφέραμε για το συγκεκριμένο βιολογικό πρόβλημα το 1926, είχε αναπτυχθεί ανεξάρτητα από τον Lotka το 1920 για να περιγράψει μια χημική αντίδραση η οποία εμφανίζει περιοδική συμπεριφορά στις συγκεντρώσεις των στοιχείων που συμμετέχουν σε αυτή! Για αυτό το λόγο ονομάζεται Lotka-Volterra μοντέλο. Εύκολα καταλαβαίνουμε ότι το κοινό στοιχείο των παραπάνω προβλημάτων (η περιοδικότητα στους πληθυσμούς ή στις συγκεντρώσεις των στοιχείων) θα πρέπει να εμφανίζεται λόγω της πεπλεγμένης δομής των συγκεκριμένων εξισώσεων.
Ξεκινάμε τη μελέτη του παραπάνω μοντέλου κάνοντας μια κατάλληλη αδιαστατοποίηση ώστε να «απλοποιήσουμε» τη μορφή των εξισώσεων. Η αδιαστατοποίηση των μεταβλητών είναι συχνά μια πολύ χρήσιμη μαθηματική διαδικασία όπως είδαμε αναλυτικά στο Κεφάλαιο 1. Για τις παραπάνω εξισώσεις επιλέγουμε τις εξής αδιάστατες μεταβλητές.
| (6.2) |
Με την επιλογή αυτή το αρχικό σύστημα εξισώσεων γίνεται (η απόδειξη αφήνεται ως άσκηση):
| (6.3) |
Το παραπάνω σύστημα εξισώσεων αποτελεί την αδιάστατη μορφή του (συνεχούς) μοντέλου Lotka-Volterra. Τα σημεία ισορροπίας του συστήματος, είναι οι τιμές των μεταβλητών για τις οποίες
Το παραπάνω σύστημα έχει δύο σημεία ισορροπίας (fixed points):
-
Α)
-
Β)
Σύντομο πρόβλημα 6.2.
Επιβεβαιώστε ότι το σύστημα (6.3) έχει τα παραπάνω σημεία ισορροπίας.
Κατόπιν εξετάζουμε την ευστάθεια του μοντέλου, ορίζοντας μικρή διαταραχή στον πληθυσμό και κάνοντας την αντίστοιχη γραμμικοποίηση, δηλαδή ανάπτυγμα Taylor και κράτημα μόνο των γραμμικών όρων.
Α) Για το πρώτο σημείο έχουμε τη διαταραχή:
Με γραμμικοποίηση θα καταλήξουμε (η απόδειξη αφήνεται ως άσκηση στον αναγνώστη), για τη χρονική εξέλιξη της διαταραχής, στις εξισώσεις:
| (6.4) |
Λύσεις του παραπάνω συστήματος είναι:
| (6.5) |
με ιδιοτιμές:
Συνεπώς η ευστάθεια καθορίζεται ως:
-
•
Αν τότε η διαταραχές και μεγαλώνουν εκθετικά, δηλαδή το σημείο είναι ασταθές.
-
•
Αν και τότε και το σημείο είναι σαγματικό (saddle point).
Β) Για το δεύτερο σημείο ορίζουμε μικρή διαταραχή
Αντίστοιχη γραμμικοποίηση δίνει:
εφόσον ισχύει: και .
Οι ιδιοτιμές του παραπάνω συστήματος είναι:
δηλαδή το σημείο στο γραμμικοποιημένο σύστημα είναι κέντρο. Η παραπάνω λύση δίνει τα παρακάτω δύο ιδιοδιανύσματα, :
| (6.6) |
Βασικό πρόβλημα του μοντέλου Lotka-Volterra είναι ότι οι λύσεις δεν είναι σταθερές (έλλειψη) με τη συνήθη έννοια, δηλαδή όπως είδαμε μια μικρή διαταραχή οδηγεί σε άλλη λύση. Αυτό είναι χαρακτηριστικό των συστημάτων διατήρησης. Παρόλα αυτά έχει εφαρμοστεί με σχετική επιτυχία σε διαφορετικά πραγματικά συστήματα.
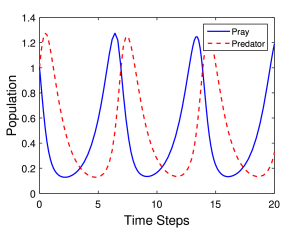
Η λύση του αρχικού συστήματος μπορεί να γίνει με αριθμητικές μεθόδους. Μια τέτοια λύση πραγματοποιήθηκε, σε γλώσσα Matlab, χρησιμοποιώντας μεθόδους Runge-Kutta (ο κώδικας υπάρχει στο τέλος του κεφαλαίου). Στα Σχήματα 6.1α και 6.1β παρουσιάζεται η εξέλιξη των πληθυσμών του θηρευτή και του θηράματος για δυο διαφορετικούς συνδυασμούς τιμές των παραμέτρων του προβλήματος, δηλαδή των σταθερών και για αρχικές τιμές των δύο πληθυσμών .
Όπως βλέπουμε η συμπεριφορά και των δύο πληθυσμών είναι περιοδική στο χρόνο.
 |
 |
Πιο συγκεκριμένα στο Σχήμα 6.1α βλέπουμε την συμπεριφορά των πληθυσμών για τιμές των παραμέτρων a=1.0, b=2.0, c=2.0, d=1.0. Στην περίπτωση αυτή οι δύο σταθερές και που αφορούν την μείωση του πληθυσμού του θηράματος, και την αντίστοιχη αύξηση του πληθυσμού του θηρευτή, λόγω της αλληλεπίδραση θηράματος – θηρευτή, είναι ίσες. Επίσης και οι δύο σταθερές που περιγράφουν την αύξηση (μείωση) του πληθυσμού του θηράματος (θηρευτή) απουσία του θηρευτή (θηράματος) είναι ίσες. Για αυτό το λόγο η συμπεριφορά των δύο πληθυσμών είναι «παρόμοια», δηλαδή η «περίοδος» και το «πλάτος» της ταλάντωσης είναι το ίδιο.
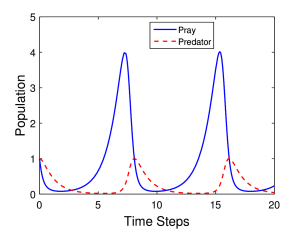
Στο Σχήμα 6.1β βλέπουμε την συμπεριφορά των πληθυσμών για τιμές των παραμέτρων . Η διαφορά σε αυτή την περίπτωση, σε σχέση με την προηγούμενη, είναι το ότι οι δύο σταθερές b και c είναι αρκετά διαφορετικές, δηλαδή η μείωση του πληθυσμού του θηράματος είναι αναλογικά μεγαλύτερη από την αύξηση του πληθυσμού του θηρευτή. Για αυτό το λόγο ο πληθυσμός του θηράματος μεταβάλλεται πολύ περισσότερο από τον πληθυσμό του θηρευτή.
Οι καμπύλες του χώρου φάσεων, ή καλύτερα επιπέδου φάσεων (phase plane, βλέπε επίσης Κεφ. 3), καθώς έχουμε δύο μεταβλητές, δίνονται από την παρακάτω διαφορική εξίσωση:
| (6.7) |
Ολοκλήρωση στο χώρο φάσεων μας δίνει:
| (6.8) |
όπου είναι σταθερά με: .
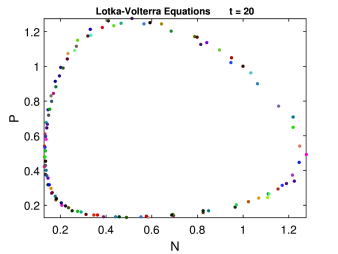
Για , και συγκεκριμένες τιμές των παραμέτρων του μοντέλου, ο χώρος φάσεων του μοντέλου φαίνεται γραφικά στο Σχήμα 6.2. Κάθε τροχιά (trajectory) είναι περιοδική λύση των αδιάστατων μεταβλητών , και στο χρόνο . Όπως βλέπουμε η μορφή του χώρου φάσεων είναι έλλειψη με κέντρο στο σημείο .
Ερώτηση κατανόησης 6.1.
Ποια από τις παραπάνω δύο περιπτώσεις περιμένετε να περιγράφει καλύτερα του πληθυσμού λαγών – αλεπούδων σε ένα δάσος;
Ερώτηση κατανόησης 6.2.
Δώστε παραδείγματα από διαφορετικούς πληθυσμούς τύπου θηρευτή – θηράματος, και εκτιμήστε (ποιοτικά) τις αντίστοιχες τιμές των σταθερών του μοντέλου Lotka – Volterra που περιμένετε.
Γενικά Μοντέλα Θηρευτή-Θηράματος
Το μοντέλο Lotka-Volterra είναι μια πρώτη περιγραφή μοντέλων τύπου θηρευτή-θηράματος. Στην παραγωγή του μοντέλου υποθέσαμε εκθετική (Μαλθουσιανό μοντέλο) αύξηση του πληθυσμού του θηράματος απουσία του θηρευτή, δηλαδή θεωρήσαμε ότι υπάρχει «άπειρο» φαγητό στο περιβάλλον για το θήραμα.
Όμως όπως είδαμε στη μελέτη πληθυσμών ενός είδους, αυτή δεν είναι γενικά ικανοποιητική υπόθεση εφόσον κάθε δεδομένο περιβάλλον έχει μια συγκεκριμένη χωρητικότητα πληθυσμού. Συνεπώς μια πρώτη επέκταση του μοντέλου Lotka-Volterra είναι να θεωρήσουμε λογιστική αύξηση για το θήραμα. Σε αυτή την περίπτωση έχουμε
Το παραπάνω σύστημα εξισώσεων είναι το λογιστικό μοντέλο Lotka-Volterra και είναι ιδιαίτερα επιτυχημένο μοντέλο για αρκετά ρεαλιστικά οικοσυστήματα δύο ειδών.
Γενικότερα μπορούμε να περιγράψουμε μοντέλα τύπου θηρευτή – θηράματος με την παρακάτω μορφή:
| (6.9) |
όπου και είναι συναρτήσεις των δύο πληθυσμών και . Η εκλογή των συναρτήσεων και γίνεται ανάλογα με το φυσικό σύστημα το οποίο μελετάμε. Παράδειγμα, μία μορφή της είναι:
| (6.10) |
όπου υποθέτουμε ότι το θήραμα, απουσία του θηρευτεί, ακολουθεί την λογιστική εξίσωση αλλά η αλληλεπίδραση θηρευτή – θηράματος, έχει μια γενικότερη, σε σχέση με τη γραμμική ως προς το γινόμενο , μορφή.
Πιο συγκεκριμένα, στην παραπάνω σχέση η συνάρτηση περιγράφει την αλλαγή του πληθυσμού του θηρευτή ως προς τις μεταβολές της πυκνότητας πληθυσμού του θηράματος. Διαφορετικές πιθανές μορφές της είναι οι:
-
•
: Αυτή η μορφή αντιστοιχεί στο μοντέλο Lotka – Volterra,
-
•
-
•
-
•
Στα παραπάνω μοντέλα: είναι θετικές σταθερές. Οι παραπάνω φαίνονται στο Σχήμα 6.3. Ως γενική παρατήρηση μπορούμε να πούμε ότι η γενική μορφή των παραπάνω μορφών της συνάρτησης πρέπει να είναι τέτοια ώστε ο όρος να είναι περίπου σταθερός για μεγάλα .
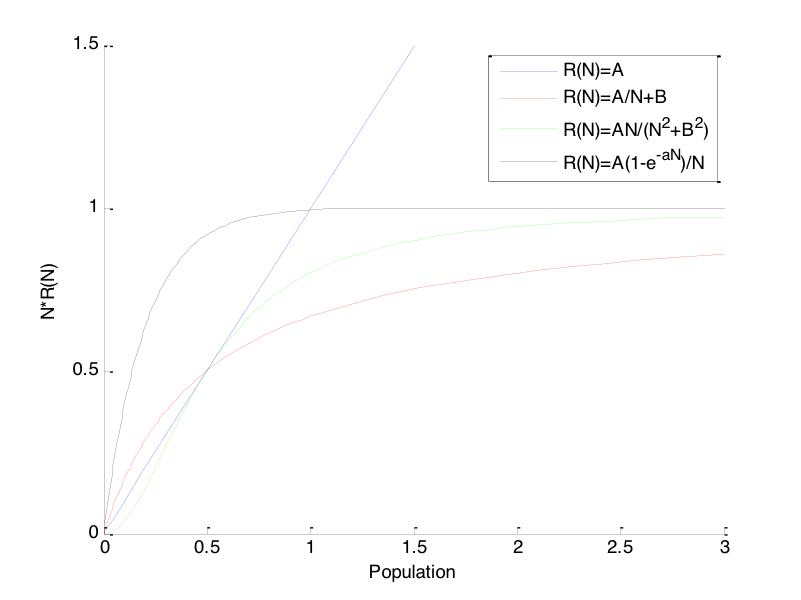
Αντίστοιχα με την παραπάνω συζήτηση, η συνάρτηση που περιγράφει την εξέλιξη του πληθυσμού του θηρευτή μπορεί επίσης να γίνει πιο «ρεαλιστική», σε σχέση με το αρχικό μοντέλο Lotka-Volterra.
Για παράδειγμα, αν υποθέσουμε ότι η χωρητικότητα του θηρευτή είναι ανάλογη της πυκνότητας του θηράματος έχουμε:
| (6.11) |
όπου : σταθερές ¿ 0.
Γενικότερα, πρέπει να επαναλάβουμε ότι η ακριβής μορφή των παραπάνω συναρτήσεων και εξαρτάται πάντα από το συγκεκριμένο πρόβλημα το οποίο μελετάμε.
Σε πρακτικό επίπεδο, αν έχουμε στατιστικά δεδομένα για κάποιο συγκεκριμένο σύστημα θηρευτή-θηράματος επιλέγουμε την συνάρτηση η οποία αναπαράγει σε καλύτερο βαθμό τα δεδομένα αυτά.
Ερώτηση κατανόησης 6.3.
Ποια είναι η βιολογική σημασία των παραπάνω τροποποιήσεων των συναρτήσεων και ; Προτείνεται αντίστοιχα παραδείγματα βιολογικών συστημάτων.
6.1.2 Μοντέλα Ανταγωνισμού
Τα μοντέλα ανταγωνισμού περιγράφουν ένα οικοσύστημα στο οποίο δύο ή περισσότεροι οργανισμοί ανταγωνίζονται για την εξεύρεση τροφής από την ίδια πηγή.
Έστω δύο είδη με πληθυσμούς και σε χρόνο , τα οποία ανταγωνίζονται για την ίδια πηγή τροφής. Για την δημιουργία του μοντέλου κάνουμε τις παρακάτω υποθέσεις:
-
•
Ο πληθυσμός κάθε είδους, απουσία του άλλου, ακολουθεί λογιστική μορφή.
-
•
Η αλληλεπίδραση (ανταγωνισμός) οδηγεί σε μείωση και των δύο πληθυσμών. Σε πρώτη προσέγγιση, η μείωση αυτή είναι ένας γραμμικός όρος, ως προς το γινόμενο .
Με βάση τις υποθέσεις αυτές, οι εξισώσεις που περιγράφουν την εξέλιξη του πληθυσμού τους είναι:
| (6.12) |
Στις παραπάνω σχέσεις , και είναι θετικές σταθερές. Ειδικότερα οι σταθερές , και εκφράζουν το μέτρο του ανταγωνισμού στο συγκεκριμένο σύστημα. Η μελέτη του μοντέλου, όπως και στα μοντέλα θηρευτή-θηράματος, γίνεται σε δύο στάδια.
Ερώτηση κατανόησης 6.4.
Ποια είναι η βιολογική σημασία όλων των σταθερών στο παραπάνω μοντέλο;
Πρώτα αδιαστατοποιούμε το σύστημα ορίζοντας τις νέες μεταβλητές:
και τις νέες παραμέτροους
Με την παραπάνω επιλογή το αρχικό σύστημα εξισώσεων γίνεται:
| (6.13) |
Σύντομο πρόβλημα 6.3.
Επιβεβαιώστε την παραπάνω αδιάστατη μορφή του μοντέλου ανταγωνισμού.
Τα σημεία ισορροπίας, και , του παραπάνω συστήματος βρίσκονται λύνοντας τις και και είναι:
-
•
,
-
•
,
-
•
και
-
•
.
Η ανάλυση ευστάθειας για κάθε σημείο ισορροπίας γίνεται όπως και στην περίπτωση του μοντέλου Lotka-Volterra, την οποία είδαμε στο προηγούμενο υποκεφάλαιο και αφήνεται ως άσκηση για τον αναγνώστη.
6.1.3 Μοντέλα Συμβίωσης
Στο τελευταίο μέρος της μελέτης μοντέλων αλληλεπιδρώντων πληθυσμών εξετάζουμε τα μοντέλα συμβίωσης. Τα μοντέλα αυτά περιγράφουν ένα οικοσύστημα στο οποίο δύο ή περισσότεροι οργανισμοί συμβιώνουν με αρμονικό τρόπο, δηλαδή η αλληλεπίδραση μεταξύ τους αποβαίνει προς όφελος όλων των ειδών. Κλασικό παράδειγμα αποτελεί ένα οικοσύστημα στο οποίο φυτά και πουλιά συμβιώνουν με αρμονικό τρόπο. Έστω και πάλι δύο είδη με πληθυσμούς N1(t) και N2(t) σε χρόνο t, τα οποία συμβιώνουν στο περιβάλλον. Το απλούστερο δυνατό μοντέλο προκύπτει κάτω από τις εξής υποθέσεις:
Υπάρχει άφθονο φαγητό και για τα δύο είδη, δηλαδή Ο πληθυσμός κάθε είδους, απουσία του άλλου, ακολουθεί εκθετική μορφή. Η αλληλεπίδραση (Συμβίωση) οδηγεί σε αύξηση και των δύο πληθυσμών. Σε πρώτη προσέγγιση, η μείωση αυτή είναι ένας γραμμικός όρος, ως προς το γινόμενο Ν1Ν2.
Συνεπώς το μοντέλο το οποίο θα περιέγραφε τους πληθυσμούς θα ήταν:
| (6.14) |
όπου και είναι θετικές σταθερές.
Το μοντέλο όμως αυτό δεν είναι ρεαλιστικό καθώς προβλέπει συνεχή αύξηση των πληθυσμών και , θυμίζει δηλαδή το Μαλθουσιανό-εκθετικό μοντέλο του ενός πληθυσμού.
Ερώτηση κατανόησης 6.5.
Ποια είναι η βιολογική σημασία της κάθε μίας από τις σταθερές στο παραπάνω μοντέλο;
Ένα πιο ρεαλιστικό μοντέλο συμβίωσης έχει προταθεί [May 1975] σε αναλογία με το μοντέλο ανταγωνισμού που είδαμε στο προηγούμενο υπό-κεφάλαιο. Δηλαδή η διαφορά από το παραπάνω μοντέλο είναι το ότι θεωρούμε πως ο πληθυσμός κάθε είδους, απουσία του άλλου, ακολουθεί λογιστική μορφή. Πιο συγκεκριμένα το μοντέλο αυτό έχει τη μορφή:
| (6.15) |
όπου , και είναι θετικές σταθερές.
Ειδικότερα οι σταθερές , και εκφράζουν το μέτρο της συμβίωσης στο συγκεκριμένο σύστημα.
Παρατήρηση 6.1.
Προσέξτε ότι αν και το μοντέλο αυτό «μοιάζει» με το μοντέλο ανταγωνισμού που είδαμε στο προηγούμενο κεφάλαιο, οι όροι συμβίωσης είναι, όπως θα περιμέναμε, θετικοί, δηλαδή η συμβίωση συνεισφέρει θετικά στην αύξηση του πληθυσμού, ενώ στο μοντέλο ανταγωνισμού ήταν αρνητικοί.
Η αδιαστατοποίηση των παραπάνω εξισώσεων γίνεται με τις νέες μεταβλητές, παρόμοια με το μοντέλο ανταγωνισμού:
Τελικά το σύστημα των αδιάστατων εξισώσεων συμβίωσης γίνεται:
| (6.16) |
Σύντομο πρόβλημα 6.4.
Εξαγάγετε την παραπάνω αδιάστατη μορφή του μοντέλου συμβίωσης.
Τα σημεία ισορροπίας, και , του παραπάνω συστήματος είναι:
-
•
,
-
•
,
-
•
, και
-
•
Η ανάλυση ευστάθειας για κάθε σημείο ισορροπίας αφήνεται ως άσκηση για τον αναγνώστη.