6.2 Διακριτά Μοντέλα Αλληλεπιδρώντων Πληθυσμών

Ας μελετήσουμε τώρα τα διακριτά μοντέλα τύπου θηράματος – θηρευτή. Έστω: $P_t$ και $Q_t$ οι πληθυσμού του θηράματος και του θηρευτή αντίστοιχα και:

$$\mathrm{\Delta }P=P_{t+1}-P_t,\mathrm{\Delta }Q=Q_{t+1}-Q_t$$

οι αλλαγές των πληθυσμών σε μία χρονική περίοδο Η γενική διακριτή μορφή των μοντέλων θηρευτή-θηράματος είναι η παρακάτω:

$$\mathrm{\Delta }P=F(P,Q),\mathrm{\Delta }Q=G(P,Q)$$

(6.17)

όπου $F$ και $G$ είναι συναρτήσεις των πληθυσμών $P$ και $Q$. Θεωρώντας ότι ο πληθυσμός του θηράματος, χωρίς θηρευτή περιγράφεται από το λογιστικό μοντέλο και υποθέτοντας ότι η αλληλεπίδραση των δύο ειδών είναι γραμμική σε όρους $PQ$, ένα τυπικό διακριτό μοντέλο θηρευτή-θηράματος είναι:

(6.18)

όπου $r,K,s,u,v>0$, σταθερές. Η παραπάνω σχέση δίνεται συνήθως και ως:

(6.19)

και αποτελεί τη διακριτή μορφή του μοντέλου Lotka-Volterra με λογιστικό όρο για τον πληθυσμού του θηράματος.

Η επίλυση του μοντέλου μπορεί να γίνει, όπως και στην περίπτωση των διακριτών μοντέλων ενός είδους, μπορεί να γίνει επαναληπτικά με χρήση υπολογιστή. Στην περίπτωσή μας η επίλυση του μοντέλου έχει γίνει με κώδικα σε γλώσσα MATLAB, ο οποίος βρίσκεται στο τέλος του κεφαλαίου.

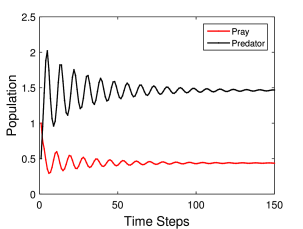
Η γραφική αναπαράσταση του παραπάνω μοντέλου για ένα συγκεκριμένο παράδειγμα φαίνεται στο Σχήμα 6.4, όπου βλέπουμε την χρονική εξέλιξη των δύο πληθυσμών, θηρευτή (prey) και θηράματος (predator), για συγκεκριμένες τιμές των παραμέτρων. Σε κάθε περίπτωση η χωρητικότητα για το θήραμα είναι Κ = 1.0 και οι αρχικές τιμές των πληθυσμών είναι $P_0=1.0$ και $Q_0=0.5$. Ουσιαστικά έχουμε κανονικοποιήσει και τους δύο πληθυσμούς με την τιμή πληθυσμού που εκφράζει την χωρητικότητα του περιβάλλοντος του θηράματος.

Γενικότερα για μικρές τιμές των όρων αλληλεπίδρασης s και v οι πληθυσμοί τείνουν «ομαλά» σε σταθερές, χρονικά ανεξάρτητες τιμές τους. Όσο όμως γίνεται πιο ισχυρή η αλληλεπίδραση των δύο πληθυσμών, τόσο περισσότερο «μη-ομαλή» γίνεται η χρονική συμπεριφορά τους. Παρακάτω παρουσιάζουμε πιο αναλυτικά δύο διαφορετικές περιπτώσεις για συγκεκριμένες τιμές των παραμέτρων ρυθμού αύξησης του πληθυσμού του θηράματος r και θνησιμότητας του πληθυσμού του θηρευτή u, και διαφορετικές τιμές των παραμέτρων $s$ και $v$.

Πιο συγκεκριμένα στο Σχήμα 6.4α βλέπουμε την χρονική εξέλιξη των δύο πληθυσμών για τιμές των παραμέτρων: $r=1.3,s=0.5,u=0.7,v=1.6$. Όπως παρατηρούμε η χρονική εξέλιξη και των δύο πληθυσμών εμφανίζει συμπεριφορά φθίνουσας ταλάντωσης, ενώ μετά από περίπου 100 χρονικά βήματα και οι δύο πληθυσμοί έχουν φτάσεις στις σταθερές, χρονικά ανεξάρτητες, τιμές του.

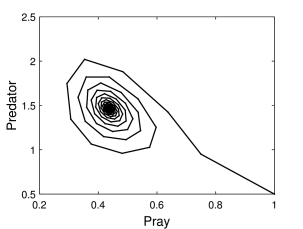
Στο Σχήμα 6.4β παρουσιάζουμε το χώρο (επίπεδο) φάσεων των δύο πληθυσμών για τις παραπάνω τιμές των παραμέτρων. Όπως βλέπουμε το επίπεδο φάσεων ακολουθεί μια «σπειροειδείς» μορφή, ενώ σε μεγάλους χρόνους, όπως περιμένουμε από το Σχήμα 6.4α, οι πληθυσμοί αποκτούν σταθερές χρονό-ανεξάρτητες τιμές, και ο χώρος φάσεων γίνεται ένα σταθερό σημείο.

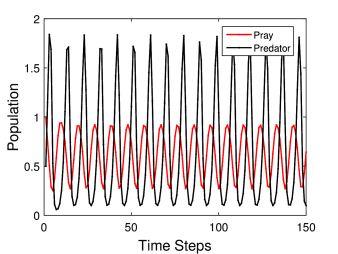
Στη δεύτερη περίπτωση (Σχήμα 6.5) παρουσιάζεται η χρονική εξέλιξη των δύο πληθυσμών για τιμές των παραμέτρων: $r=1.0,s=0.5,u=0.7,v=2.8$. Εδώ ο όρος αύξησης του πληθυσμού του θηρευτή λόγω των «επαφών» του με το θήραμα είναι ιδιαίτερα μεγάλος, με άλλα λόγια ο πληθυσμός του επηρεάζεται σε πολύ μεγαλύτερο βαθμό. Αυτή ακριβώς η ισχυρή αλληλεπίδραση οδηγεί σε μεγάλες μεταβολές και των δύο πληθυσμών, ιδιαίτερα του πληθυσμού του θηρευτή. Επίσης οι μεταβολές αυτές είναι σχεδόν περιοδικές για όλο το εύρος των χρόνων που μελετάμε. Πιο συγκεκριμένα ο πληθυσμός του θηράματος (prey) μεταβάλλεται από περίπου 0.2 σε 0.9, θυμηθείτε ότι η χωρητικότητα του περιβάλλοντος για το θήραμα είναι 1.0. Ειδικά για τον πληθυσμού του θηρευτή (predator) η ισχυρή αλληλεπίδραση οδηγεί σε ένα μεγάλο εύρος τιμών του πληθυσμού, από περίπου 0.05 σε 1.8.

Σε αναλογία με την παραπάνω ανάλυση υπάρχουν διαφορετικά διακριτά μοντέλα ανταγωνισμού. Παρακάτω, ως παράδειγμα, αναφέρουμε τρία από αυτά. Σε κάθε περίπτωση οι μεταβλητές ορίζονται όπως και στα διακριτά μοντέλα τύπου θηρευτή-θηράματος, δηλαδή Pt και Qt είναι οι πληθυσμοί των δύο ειδών κατά τη χρονική στιγμή t, και οι μεταβολές (αλλαγή) των πληθυσμών σε μια χρονική περίοδο ορίζονται ως:

$$\mathrm{\Delta }P=P_{t+1}-P_t,\mathrm{\Delta }Q=Q_{t+1}-Q_t.$$

Πρώτο, και σχετικά απλούστερο, μοντέλο ανταγωνισμού είναι το παρακάτω:

(6.20)

όπου $r,u,\mathrm{{\rm K}}$ είναι σταθερές του μοντέλου. Στο παραπάνω μοντέλο κάθε πληθυσμός απουσία του άλλου ακολουθεί το Λογιστικό μοντέλο. Πρόβλημα του μοντέλου είναι ότι σε μεγάλους χρόνους όποιο είδος έχει τον μεγαλύτερο ρυθμό ανάπτυξης ($r$ ή $u$) επικρατεί πλήρως, δηλαδή το άλλο είδος εξαφανίζεται!

Δεύτερο, και σχετικά πιο ρεαλιστικό είναι το παρακάτω μοντέλο:

(6.21)

Το μοντέλο αυτό εμπεριέχει ένα επιπλέον αρνητικό όρο αλληλεπίδρασης.

Περαιτέρω και ιδιαίτερα σημαντικά παραδείγματα αυτής της κατηγορίας είναι μοντέλα που μελετούν την ανάπτυξη ιών όπως ο HIV (Human Immunodeficiency Virus) ο οποίος οδηγεί στο AIDS.

Όπως και παραπάνω υπάρχουν διαφορετικά πιθανά διακριτά μοντέλα συμβίωσης δύο πληθυσμών. Ένα πρώτο μοντέλο με γραμμικούς μόνο όρους ως προς την αλληλεπίδραση PQ είναι το ακόλουθο:

(6.23)

Το μοντέλο όπως και στη συνεχή του μορφή δεν είναι ιδιαίτερα ρεαλιστικό καθώς οδηγεί σε συνεχή αύξηση των $P,Q$. Ένα πιο ρεαλιστικό μοντέλο είναι το παρακάτω:

(6.24)