4.2 Δυναμική δινών σε ρευστά και στη συμπυκνωμένη ύλη
4.2.1 Δίνες σε ρευστά και στη συμπυκνωμένη ύλη
Συνήθεις δίνες σε ρευστά
Οι δίνες είναι φυσικές οντότητες οι οποίες εμφανίζονται και παίζουν σημαντικό ρόλο σε πάρα πολλά φυσικά συστήματα. Οι πιο γνωστές δίνες είναι αυτές που εμφανίζονται στα ρευστά. Στη μηχανική ρευστών είναι γνωστό ότι οι δίνες (fluid vortices) παίζουν κεντρικό ρόλο στην περιγραφή και κατανόηση τόσο την κίνησης των ρευστών όσο και πιο περίπλοκων φαινομένων όπως η τυρβώδης ροή. Στην ατμόσφαιρα είναι γνωστοί οι στρόβιλοι οι οποίοι εμφανίζονται σε μικρές αλλά και σε εξαιρετικά μεγάλες διαστάσεις [31].
Η περιγραφή της κίνησης των ρευστών και άρα και της δυναμικής των δινών βασίζεται στις εξισώσης της μηχανικής ρευστών οι οποίες είναι μη-γραμμικές μερικές διαφορικές εξισώσεις. Απλοποίηση της περιγραφής δινών προκύπτει στην περίπτωση που θεωρήσουμε ότι κάθε δίνη είναι μακριά από κάθε άλλη και άρα μπορούμε να θεωρήσουμε ότι η σημαντική κεντρική περιοχή της δίνης είναι μικρού μεγέθους σε σύγκριση με την απόσταση μεταξύ τους. Τότε μπορούμε να περιγράψουμε προσεγγιστικά τη θέση κάθε δίνης με ένα σημείο. Λέμε τότε ότι έχουμε την προσέγγιση σημειακών δινών.
Στην περιγραφή δινών πολύ χρήσιμη είναι μία ποσότητα η οποία λέγεται στροβιλότητα (vorticity, ) και της οποίας το ολοκλήρωμα στην επιφάνεια του ρευστού
δίνει την ισχύ της δίνης. Επιπλέον, μπορεί να δειχθεί ότι για μία δίνη οι ποσότητες
| (4.52) |
είναι διατηρήσιμες. Αυτές οι ποσότητες μπορούν να θεωρηθούν ως ένας ορισμός της θέσης μίας δίνης (μετά από κατάλληλη κανονικοποίηση). Στην περίπτωση που θεωρούμε τη δίνη σημειακή μπορούμε εύκολα να δούμε ότι τα παραπάνω ολοκληρώματα δίνουν τη θέση της σημειακής δίνης πολλαπλασιασμένη με την ισχύ της.
Δίνες σε υπερρευστά
Ορισμένα ρευστά επιδεικνύουν ασυνήθιστες ιδιότητες όταν βρίσκονται σε ιδιαίτερα χαμηλές θερμοκρασίες. Η πιο εντυπωσιακή ίσως ιδιότητα τους είναι ότι ρέουν χωρίς η κίνησή τους να επιβραδύνεται από φαινόμενα τριβής. Υγρά που παρουσιάζουν αυτή την ιδιότητά ονομάζονται υπερρευστά. Τα σημαντικότερα υπερρευστά είναι το στοιχείο Ήλιο σε θερμοκρασίες Kelvin το οποίο βρίσκεται τότε σε υγρή κατάσταση. Επίσης, υπερρευστά είναι οι ατμοί αλκαλικών μετάλλων (Li, Na, K, Rb, Cs) οι οποίοι παγιδεύονται με μαγνητικά πεδία και ψύχονται σε θερμοκρασίες nanoKelvin με οπτικά (LASER) και άλλα μέσα.
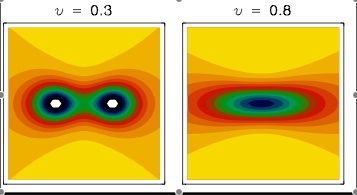
Μία επιπλέον ιδιότητα των υπερρευστών είναι ότι οι δίνες που δημιουργούνται σε αυτά έχουν ισχύ η οποία είναι ακέραιο πολλαπλάσιο μιας βασικής ποσότητας ισχύος. Τέτοιες δίνες ονομάζονται κβαντισμένες (quantized vortices). Η ιδιότητα αυτή των δινών σχετίζεται πάντως με την ιδιότητα της ροής χωρίς τριβή. Τα υπερρευστά και οι δίνες τους μελετώνται με τη βοήθεια των νόμων της κβαντικής φυσικής. Σε ορισμένες περιπτώσεις το υπερρευστό καθώς και οι δίνες τους μπορούν να περιγραφούν από ένα μιγαδικό πεδίο το οποίο ονομάζεται κυματοσυνάρτηση του υπερρευστού. Η κυματοσυνάρτηση υπακούει μη-γραμμικές μερικές διαφορικές εξισώσεις. Οι εξισώσεις όμως αυτές διαφέρουν πολύ από εκείνες για τα συνήθη ρευστά στα οποία αναφερθήκαμε παραπάνω.
Ένα σημαντικό σημείο είναι ότι η στροβιλότητα στα υπερρευστά συνδέεται με τοπολογικά χαρακτηριστικά του πεδίου που περιγράφει το υπερρευστό, δηλαδή της κυματοσυνάρτησής του. H ολική ισχύς παίρνει διάκριτες τιμές και έχει την ερμηνεία ενός τοπολογικού αριθμού. Διατηρήσιμες ποσότητες ανάλογες των (4.52) υπάρχουν και σε αυτή την περίπτωση.
Κάτω από ορισμένες προϋποθέσεις μπορούμε να κάνουμε την προσέγγιση των σημειακών δινών και στο παρόν σύστημα. Έτσι μπορούμε να απλοποιήσουμε σημαντικά τη μελέτη της δυναμικής τους.
Μαγνητικές δίνες
Παρά το ότι συνδέουμε συνήθως τις δίνες με τα ρευστά, η αλήθεια είναι ότι οι δίνες, ως μαθηματικές δομές διανυσματικών πεδίων, εμφανίζονται σε πολλά διαφορετικά συστήματα. Ένα παράδειγμα είναι τα μαγνητικά υλικά στα οποία έχουμε τις λεγόμενες μαγνητικές δίνες.
Τα μαγνητικά συστήματα τα οποία έχουν ιδαίτερο εργαστηριακό ενδιαφέρον είναι υπέρλεπτα υμένια (φιλμ) από σιδηρομαγνητικά υλικά. Η μικροσκοπική δομή σε ένα μαγνητικό υλικό περιγράφεται από ένα διανυσματικό πεδίο το οποίο παριστάνει τη μαγνήτιση του υλικού σε κάθε σημείο του υμενίου. Ένα ενδιαφέρον ερώτημα είναι τι δομές σχηματίζει η μαγνήτιση στο υλικό και ποιά είναι η εξέλιξή τους στον χρόνο. Για παράδειγμα, αυτό το ερώτημα αποκτά ιδιαίτερο ενδιαφέρον όσον αφορά στον μαγνητικό δίσκο ενός υπολογιστή όπου η πληροφορία αποθηκεύεται σε κάποιες ειδικές δομές της μαγνήτισης, ενώ για τα γραφτεί ή να σβηστεί μία πληροφορία θα πρέπει οι δομές αυτές να μεταβληθούν με ελεγχόμενο τρόπο.
Μία αριθμητική προσομοίωση μαγνητικών δομών οι οποίες χαρακτηρίζονται ως μαγνητικές δίνες παρουσιάζονται στο σχήμα 4.2. Βλέπουμε ότι στην περίπτωση των μαγνητικών δινών δεν υπάρχει ροή πραγματικού ρευστού. Συμβαίνει όμως να μπορούμε να ορίσουμε μία ποσότητα η οποία έχει ομοιότητες με τη στροβιλότητα () στα ρευστά. Η δίνει μεταβολές της μαγνήτισης στον χώρο (χωρικές παραγώγους της ) και σχετίζεται άμεσα με κάποια τοπολογικά χαρακτηριστικά της μαγνήτισης. Η ισχύς της δίνης είναι ένας ακέραιος αριθμός, όπως συμβαίνει και με την ισχύ των δινών σε υπερρευστά.
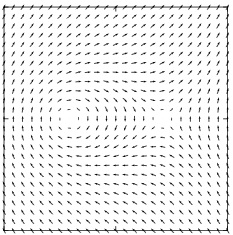
Από τη θεωρία προκύπτουν διατηρήσιμες ποσότητες της μορφής
| (4.53) |
οι οποίες είναι απολύτως ανάλογες με τις (4.52). Μπορεί να δειχθεί ότι, στην περίπτωση που θεωρήσουμε ότι οι μαγνητικές δίνες είναι σημειακές, η δυναμική τους συμπεριφορά μοντελοποιείται από εξισώσεις ανάλογες με αυτές των δινών σε ρευστά.
4.2.2 Δυναμική σημειακών δινών
Οι εξισώσεις κίνησης για αλληλεπιδρώσες δίνες, στην προσέγγιση που αυτές θεωρηθούν σημειακές, δόθηκαν από τον Helmholtz [14]. Στο μοντέλο που εισήγαγε ο Helmholtz θεωρεί ότι η στροβιλότητα περιορίζεται μέσα σε ορισμένες περιοχές που έχουν σχήμα ευθύγραμμων κυλίνδρων με ελάχιστη διάμετρο, οι οποίες λέγονται vortex filaments (νήματα δινών). Κάθε μία από αυτές τις δίνες χαρακτηρίζεται από την ισχύ της και σχετίζεται με την κυκλοφορία του ρευστού γύρω από το κέντρο της δίνης. Θα περιοριστούμε σε ροές σε δύο διαστάσεις, δηλαδή, θα θεωρήσουμε ότι η συμπεριφορά της δίνης (του vortex filament) μέσα στο υγρό ακολουθεί τη συμπεριφορά της δίνης την οποία παρατηρούμε στην επιφάνεια του υγρού. Σε αυτή την προσέγγιση λέμε ότι έχουμε σημειακές δίνες.
Κάθε σημειακή δίνη περιγράφεται πλήρως από τη θέση της στο επίπεδο , ώστε ο στόχος της μελέτης είναι η κίνηση της θέσης τους στο επίπεδο. Ξεκινάμε θεωρώντας δύο δίνες οι οποίες βρίσκονται σε κοντινή απόσταση μεταξύ τους, ώστε αλληλεπιδρούν μέσω της κίνησης του ρευστού ανάμεσά τους. Οι εξισώσεις κίνησης για δύο αλληλεπιδρώσες δίνες στο επίπεδο δίνονται από τις [19, 2]
| (4.54) |
όπου είναι οι θέσεις των δύο δινών στο επίπεδο, είναι οι ισχύες τους και
| (4.55) |
είναι η απόσταση μεταξύ των δινών.
Θα γράψουμε την παρακάτω συνάρτηση η οποία έχει ειδική σημασία σε αυτό το σύστημα:
| (4.56) |
Η εξαρτάται από τη σχετική θέση μεταξύ των δινών και έχει την ιδιότητα ότι διατηρείται κατά την κίνηση:
| (4.57) |
Λέμε ότι η δίνει το δυναμικό αλληλεπίδρασης μεταξύ ενός ζεύγους δινών και μάλιστα αποτελεί την ενέργεια του συστήματος. Θα μπορούσε κανείς να πει ότι το σύστημα αυτό έχει μόνο δυναμική ενέργεια (η ενέργειά του δεν έχει κινητικό όρο) και αυτή προέρχεται από αλληλεπιδράσεις μεταξύ δινών.
Μία απομονωμένη δίνη
Ας περιοριστούμε στην περιγραφή μίας απομονωμένης δίνης. Τις εξισώσεις κίνησης μπορούμε να τις εξαγάγουμε από τις (4.54) θέτωντας και ακολούθως (για την απλοποίηση του συμβολισμού) . Οι εξισώσεις κίνησης για τις μεταβλητές είναι
| (4.58) |
Οι παραπάνω εξισώσεις έχουν τη μορφή ιδιαίτερα απλών νόμων διατήρησης. Οι λύσεις τους είναι και οδηγούν στο συμπέρασμα ότι μία απομονωμένη δίνη (δηλαδή μία δίνη που δεν δέχεται δυνάμεις) είναι πάντα στάσιμη σε ένα ρευστό.
Οι απλοί αυτοί νόμοι διατήρησης βρίσκονται σε αντιστοιχία με τους νόμους διατήρησης για τα στις Εξ. (4.52) για τους οποίους μιλήσαμε στη γενική εισαγωγή για τις δίνες. Αυτή είναι μία πρώτη ένδειξη ότι το μοντέλο που χρησιμοποιούμε αποδίδει βασικές δυναμικές ιδιότητες των δινών.
Σύντομο πρόβλημα 4.5.
(Μη-στατικότητα ζεύγους δινών) Δείξτε ότι για οι Εξ. (4.54) δεν έχουν στατικές λύσεις, δηλαδή, δεν έχουν λύσεις της μορφής
4.2.3 Ζεύγος αλληλεπιδρουσών δινών: Διατηρήσιμες ποσότητες
Χρησιμοποιώντας τις Εξ. (4.54) βρίσκουμε ότι
δηλαδή, οι ακόλουθες είναι διατηρήσιμες ποσότητες:
| (4.59) |
Παρατηρούμε ότι αυτές οι ποσότητες είναι ανάλογες των ποσοτήτων (4.52) οι οποίες δίνουν τη θέση μίας δίνης στη μηχανική ρευστών και επίσης των (4.53) για τη θέση μίας μαγνητικής δίνης. Άρα η απλοποιημένη θεωρία μας δίνει ένα από τα βασικά αποτελέσματα της πλήρους θεωρίας (είτε στη μηχανική ρευστών είτε στη θεωρία για μαγνητικά υλικά, είτε και σε άλλες θεωρίες).
Μπορούμε να ορίσουμε τη μέση θέση για ζεύγος δινών ως
| (4.60) |
Αυτές είναι οι ποσότητες κανονικοποιημένες ως προς την ολική ισχύ :
Ο ορισμός του είναι ανάλογος του ορισμού κέντρου μάζας για ένα σύστημα υλικών σωμάτων. Το διάνυσμα μπορεί να ονομαστεί οδηγός της κίνησης (guiding center) σε αναλογία με τις αντίστοιχες ποσότητες στην περίπτωση κίνησης φορτίων σε μαγνητικό πεδίο.
Παρατήρηση 4.9.
Ο οδηγός της κίνησης για ζεύγος δινών στην Εξ. (4.60) είναι διατηρήσιμο μέγεθος. Βλέπουμε λοιπόν ότι ένα ζεύγος δινών κινείται έτσι ώστε η μέση θέση του συστήματος να παραμένει σταθερή.
Παρατήρηση 4.10.
Ο νόμος διατήρησης του οδηγού κίνησης αποκλείει την περίπτωση δύο όμοιες δίνες () να κινούνται σε ελεύθερη κίνηση προς την ίδια κατεύθυνση.
Ο ορισμός (4.60) του οδηγού της κίνησης είναι αποδεκτός μόνο όταν . Η αστοχία του ορισμού για τον οδηγό κίνησης όταν δείχνει ότι αυτή είναι μιά ειδική περίπτωση και θα πρέπει να μετεληθεί χωριστά. φυσικά, σε αυτήν την περίπτωση δεν ισχύουν τα συμπεράσματα που αναφέραμε στις παραπάνω παρατηρήσεις.
Για το μοντέλο που μελετάμε είναι επίσης γνωστό ότι η ποσότητα
| (4.61) |
είναι διατηρήσιμη και είναι γνωστό ότι αυτή αντιστοιχεί στη στροφορμή του συστήματος δινών. Ο νόμος διατήρησης αποδεικνύεται με άμεσο υπολογισμό
όπου για τις χρονικές παραγώγους χρησιμοποιήσαμε τις Εξ. (4.54).
Στα επόμενα θα μελετήσουμε δύο ειδικές περιπτώσεις χρησιμοποιώντας τις διατηρήσιμες ποσότητες τις οποίες είδαμε σε αυτήν την παράγραφο.
Ερώτηση κατανόησης 4.2.
Εάν υπάρξει εξωτερική δύναμη τότε είναι δυνατόν να μην διατηρείται ο οδηγός της κίνησης και ενδεχομένως να έχουμε συνολική μετατόπιση του συστήματος των δινών. Πώς θα μπορούσαν να γραφούν οι εξισώσεις κίνησης ώστε να περιλαμβάνουν μία εξωτερική δύναμη;
4.2.4 Ζεύγος αλληλεπιδρουσών δινών: Τροχιές
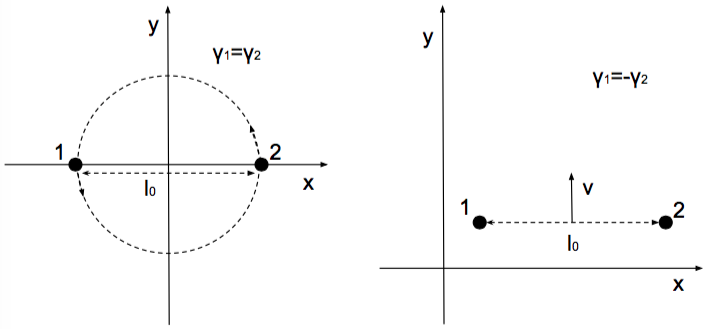
Περίπτωση
Θεωρούμε δύο δίνες οι οποίες είναι όμοιες, δηλαδή έχουν την ίδια ισχύ και για απλότητα παίρνουμε . Οι διατηρήσιμες ποσότητες όπως δίνονται στις εξισώσεις (4.56), (4.59), (4.61) είναι
| (4.62) |
Παρατήρηση 4.11.
Μπορούμε να εκμεταλλευτούμε την ύπαρξη ενός ασυνήθιστα μεγάλου αριθμού διατηρήσιμων ποσοτήτων και να μελετήσουμε το πρόβλημα της κίνησης των δινών χωρίς να χρειαστεί να λύσουμε και πάλι τις εξισώσεις κίνησης.
Οι και είναι ανεξάρτητες μεταξύ τους και επίσης η τιμή τους μπορεί να αλλάξει με απλή μετάθεση της αρχής του συστήματος συντεταγμένων. Εκλέγουμε λοιπόν την αρχή του συστήματος συντεταγμένων έτσι ώστε . Ώστε ισχύουν οι
| (4.63) |
Από τη διατήρηση της ενέργειας έχουμε
| (4.64) |
Βλέπουμε ότι η απόσταση μεταξύ των δινών παραμένει σταθερή και στη σταθερή τιμή της δώσαμε το σύμβολο . Με τη βοήθεια των (4.63) η απόσταση μεταξύ των δύο δινών γράφεται
Παράδειγμα 4.9.
Δείξτε ότι η διατήρηση της στροφορμής δεν δίνει επιπλέον αποτελέσματα από αυτά που ήδη πετύχαμε με τις .
Επίλυση.
Χρησιμοποιώντας τις Εξ. (4.63) γράφουμε τη στροφορμή ως
Άρα ο νόμος διατήρησης της μας δίνει το αποτέλεσμα που ήδη γνωρίζουμε από τον νόμο διατήρησης της .
Συμπερασματικά, η Εξ. (4.63) δείχνει ότι οι δίνες βρίσκονται (για όλους τους χρόνους) σε αντιδιαμετρικές θέσεις ως προς ένα σημείο το οποίο έχει εκλεγεί ως αρχή των αξόνων. Η Εξ. (4.64) δείχνει ότι βρίσκονται σε σταθερή μεταξύ τους απόσταση σε κάθε χρονική στιγμή. Άρα οι δίνες κινούνται σε κύκλο με κέντρο την αρχή των αξόνων και διάμετρο .
Για να βρούμε τη γωνιακή ταχύτητα περιστροφής θα πρέπει να ανατρέξουμε στις εξισώσεις κίνησης, αφού οι διατηρήσιμες ποσότητες δεν περιέχουν τον χρόνο. Θεωρούμε τις δύο από τις Εξ. (4.54) οι οποίες δίνουν τις χρονικές παραγώγους των μεταβλητών και χρησιμοποιούμε τις σχέσεις (4.63), (4.64) τις οποίες βρήκαμε από τους νόμους διατήρησης. Έτσι, βρίσκουμε για τη θέση τις διαφορικές εξισώσεις:
| (4.65) |
Παίρνοντας τη χρονική παράγωγο της πρώτης και χρησιμοποιώντας τη δεύτερη βρίσκουμε
| (4.66) |
Μία ανάλογη εξίσωση μπορούμε να εξάγουμε και για την , καθώς επίσης και για τις . Οι εξισώσεις αυτές περιγράφουν περιοδική κίνηση με γωνιακή συχνότητα
| (4.67) |
Παρατήρηση 4.12.
Δύο δίνες με κινούνται σε κυκλική τροχιά με γωνιακή συχνότητα αντιστρόφως ανάλογη του τετραγώνου της σταθερής μεταξύ τους αποστάσεως.
Σύντομο πρόβλημα 4.6.
Ποία είναι η γωνιακή ταχύτητα περιστροφής του ζεύγους για ;
Ερώτηση κατανόησης 4.3.
Το ζεύγος δινών αυτής της παραγράφου περιστρέφεται αριστερόστροφα ή δεξιόστροφα; Για ποιό ζεύγος δινών θα ήταν δυνατόν να έχουμε περιστροφή αντίθετης φοράς;
Περίπτωση
Θεωρούμε δύο δίνες οι οποίες έχουν ίση και αντίθετη ισχύ και για απλότητα παίρνουμε . Οι διατηρήσιμες ποσότητες όπως δίνονται στις εξισώσεις (4.56), (4.59), (4.61) είναι
| (4.68) |
Με κατάλληλη στροφή του συστήματος συντεταγμένων μπορούμε να εκλέξουμε τον άξονα να είναι παράλληλος στην ευθεία που περνάει από τις δύο δίνες (στην αρχική τους θέση). Επίσης, παίρνουμε τον άξονα έτσι ώστε να διχοτομεί το ευθύγραμμο τμήμα που ενώνει τις δύο δίνες. Άρα, αν είναι η απόσταση μεταξύ των δινών τότε αυτές βρίσκονται αρχικά στις θέσεις . Έτσι έχουμε επιτύχει να ισχύει
| (4.69) |
Αφού η διατηρείται, θα έχουμε ότι για κάθε χρονική στιγμή. Επίσης, παρατηρούμε ότι
άρα η απόσταση μεταξύ των δινών είναι σταθερή και θέτουμε . Η διατηρήσιμη ποσότητα είναι ισοδύναμη με την πρόταση που μόλις δείξαμε, ότι η απόσταση παραμένει σταθερή. Άρα η διατηρήσιμη ποσότητα περιέχεται στις . Ειδικότερα, αφού έχουμε εκλέξει έχουμε
Για την τελευταία διατηρήσιμη ποσότητα, τη στροφορμή , έχουμε
ώστε συμπεραίνουμε ότι το άθροισμα είναι επίσης διατηρήσιμη ποσότητα. Συγκεντρώνοντας το τελευταίο αποτέλεσμα και τη διατήρηση του έχουμε
| (4.70) |
δηλαδή, οι συντεταγμένες παραμένουν αμετάβλητες κατά τη διάρκεια της κίνησης.
Συμπερασματικά, η Εξ. (4.70) δείχνει ότι οι δίνες δεν κινούνται κατά τη διεύθυνση του άξονα (δηλαδή, κατά τη διεύθυνση της ευθείας που τις συνδέει). Είναι δυνατόν να κινούνται μόνο κατά τη διεύθυνση (δηλαδή, κάθετα στην ευθεία που τις συνδέει).
Για να βρούμε την ταχύτητα κίνησης του ζεύγους θα πρέπει να ανατρέξουμε στις εξισώσεις κίνησης. Παρατηρούμε ότι οι ταχύτητες των δύο δινών είναι ίσες (αφού για κάθε χρονική στιγμή) και θέτουμε . Οπότε από τη δεύτερη Εξ. (4.54) έχουμε
Στην περίπτωση που μελετάμε είναι , ώστε οι δίνες έχουν ταχύτητα
με φορά προς τον θετικό άξονα .
Παρατήρηση 4.13.
Δύο δίνες με κινούνται με την ίδια ταχύτητα κάθετα στο ευθύγραμμο τμήμα που τις συνδέει. Η ταχύτητά τους είναι σταθερή και αντιστρόφως ανάλογη της σταθερής απόστασης μεταξύ των δινών.
Η κατεύθυνση της ταχύτητας εξαρτάται από το πρόσημο του . Αν αντιστρέψουμε τις θέσεις των δινών αντιστρέφεται και η φορά της κίνησης.
Σύντομο πρόβλημα 4.7.
Ποία είναι η ταχύτητα του ζεύγους για ;
Γενική περίπτωση
Θεωρούμε δύο δίνες με ισχύες και . Θα θέλαμε να βρούμε την τροχιά τους χρησιμοποιώντας μόνο τις διατηρήσιμες ποσότητες. Θεωρούμε τις ως σταθερές και γράφουμε τις
| (4.71) |
Επίσης, από τη διατήρηση της ενέργειας προκύπτει ότι , όπου είναι η σταθερή απόσταση μεταξύ των δύο δινών και μπορούμε να γράψουμε
| (4.72) |
Αντικαθιστούμε τις Εξ. (4.71) στην τελευταία και βρίσκουμε
Χρησιμοποιούμε τον ορισμό του οδηγού κίνησης (4.60), θέτουμε την ολική ισχύ του συστήματος
και έχουμε την τροχιά της δίνης σε πιο συμπαγή μορφή:
| (4.73) |
Δηλαδή, έχουμε για τη δίνη κίνηση επάνω σε κύκλο με κέντρο τον οδηγό κίνησης και ακτίνα . Ομοίως, για τη δίνη βρίσκουμε
| (4.74) |
Παρατήρηση 4.14.
Δύο δίνες για τις οποίες κάνουν κυκλική κίνηση με κέντρο τον κοινό οδηγό κίνησης αλλά με διαφορετικές ακτίνες. Ο λόγος των ακτίνων των διαγραφόμενων κύκλων είναι , όπου η ισχυρότερη δίνη (αυτή με το μέγιστο ) διαγράφει κύκλο με μικρότερη ακτίνα.
Για να βρούμε τη συχνότητα περιστροφής χρησιμοποιούμε το αποτέλεσμα ότι και αντικαθιστούμε τις Εξ. (4.71) στις εξισώσεις κίνησης. Bρίσκουμε ότι το σημείο κάνει κυκλική κίνηση με κέντρο τον οδηγό κίνησης και γωνιακή συχνότητα
| (4.75) |
Ομοίως βρίσκουμε ότι το κινείται με την ίδια γωνιακή συχνότητα.
Ερώτηση κατανόησης 4.4.
Σύντομο πρόβλημα 4.8.
Σχεδιάστε τις τροχιές για δύο δίνες με .
4.2.5 Σύστημα αλληλεπιδρουσών δινών
Θα θεωρήσουμε ένα σύστημα από δίνες με ισχύες , οι οποίες αλληλεπιδρούν μεταξύ τους. Η θέση κάθε δίνης είναι , ώστε χρειαζόμαστε μεταβλητές για την πλήρη περιγραφή του συστήματος. Θεωρούμε ότι οι δίνες αλληλεπιδρούν κατά ζεύγη με δυναμικό της μορφής (4.56). Ώστε, για το πλήρες σύστημα, θα έχουμε ενέργεια αλληλεπίδρασης η οποία είναι γενίκευση της (4.56) [27]:
| (4.76) |
όπου είναι η απόσταση μεταξύ δύο τυχόντων δινών και . Στο παραπάνω διπλό άθροισμα έχουμε επιλέξει να αθροίσουμε σε όλα τα , όμως αθροίζουμε μόνο στα . Αυτό εξασφαλίζει δύο συνθήκες: κάθε ζεύγος λαμβάνεται υπόψιν μία φορά στο άθροισμα και επίσης εξαιρείται ο όρος για (δεν υπάρχει αλληλεπίδραση κάθε δίνης με τον εαυτό της).
Οι εξισώσεις κίνησης μπορούν να γραφούν σε αναλογία με το σύστημα εξισώσεων (4.54) για ζεύγος δινών. Έχουμε το σύστημα εξισώσεων
| (4.77) |
Αυτό το σύστημα εξισώσεων μας λέει ότι κάθε δίνη αλληλεπιδρά με κάθε μία από τις άλλες δίνες κατά τον τρόπο που περιγράψαμε στην περίπτωση ζεύγους δινών και οι αλληλεπιδράσεις προστίθενται.
Μπορούμε να δείξουμε ότι γενικεύσεις των διατηρήσιμων ποσοτήτων που είδαμε για την περίπτωση δύο δινών αποτελούν διατηρήσιμες ποσότητες στο σύστημα των δινών. Αυτές είναι η ενέργεια (4.76), επίσης οι
| (4.78) |
και τέλος η ποσότητα (η οποία μπορεί να δειχθεί ότι έχει την έννοια της στροφορμής)
| (4.79) |
4.2.6 Σύστημα τριών δινών
Θα μελετήσουμε ένα σύστημα τριών δινών με ισχύες [12, 2]. Μπορούμε να θεωρήσουμε ότι οι δίνες βρίσκονται στις κορυφές τριγώνου στις θέσεις . Οι εξισώσεις κίνησης είναι οι (4.77) τις οποίες θα εφαρμόσουμε για , ώστε παίρνουμε το σύστημα
| (4.80) |
Έχουμε χρησιμοποιήσει τον συμβολισμό
| (4.81) |
για το μήκος των πλευρών του τριγώνου.
Προκύπτει ότι το σύστημα (4.80) για τις τρεις δίνες είναι πλήρως ολοκληρώσιμο, δηλαδή, όλες οι λύσεις του μπορούν να δωθούν σε κλειστή μορφή [12, 3]. Δεν θα δώσουμε εδώ την πλήρη ολοκλήρωση του συστήματος, όμως θα αναφερθούμε σε κάποιες εξισώσεις και λύσεις οι οποίες έχουν ιδιαίτερα απλές μορφές.
Η πρώτη σημαντική απλοποίηση των έξι εξισώσεων (4.80) προκύπτει αν γράψουμε τις εξισώσεις κίνησης για τα μήκη των πλευρών του τριγώνου και . Παραγωγίζουμε λοιπόν τις ποσότητες στις Εξ. (4.81) και χρησιμοποιούμε τις πλήρεις εξισώσεις (4.80), ώστε τελικά βρίσκουμε
| (4.82) |
Η ποσότητα είναι η επιφάνεια του τριγώνου την οποία θεωρούμε με θετικό πρόσημο αν οι δίνες εμφανίζονται αριστερόστροφα στο επίπεδο ενώ τη θεωρούμε με αρνητικό πρόσημο αν εμφανίζονται δεξιόστροφα. Γνωρίζουμε από την Γεωμετρία ότι το μέτρο της επιφάνειας δίνεται ως
| (4.83) |
δηλαδή, εκφράζεται χρησιμοποιώντας μόνο τα μήκη των πλευρών του τριγώνου. Έχουμε το σημαντικό αποτέλεσμα για τη δυναμική των τριών δινών, ότι οι εξισώσεις (4.82) είναι ένα κλειστό σύστημα ως προς δηλαδή περιέχουν μόνο αυτές τις τρεις ποσότητες (τις αποστάσεις μεταξύ των δινών).
Το αρχικό σύστημα εξισώσεων περιέχει συνολικά έξι ποσότητες και βέβαια η θέση στον χώρο του συστήματος τριών δινών δεν μπορούν να προσδιορισθούν μόνο από τη γνώση των πλευρών του τριγώνου . Θα χρειαζόμασταν επιπλέον τη θέση του τριγώνου στον χώρο και γωνίες για να προσδιορίσουμε τον προσανατολισμό του.
Όμως, οι εξισώσεις (4.82) δείχνουν ότι μπορούμε να μελετήσουμε τη χρονική εξέλιξη του τριγώνου με τρόπο ανεξάρτητο από την κίνηση ή περιστροφή του στον χώρο. Αυτό μπορεί να μας βοηθήσει ιδιαίτερα να βρούμε ειδικές λύσεις για το σύστημα. Μία τέτοια λύση είναι η
| (4.84) |
η οποία βέβαια δείχνει ότι τρεις δίνες η οποίες βρίσκονται αρχικά () στις κορυφές ενός ισοπλεύρου τριγώνου θα συνεχίσουν να ισαπέχουν για κάθε χρόνο .
Περισσότερα αποτελέσματα θα μας βοηθήσουνε να βγάλουμε οι διατηρήσιμες ποσότητες τις οποίες ήδη γνωρίζουμε ότι έχει το σύστημα. Τέτοιες διατηρήσιμες ποσότητες είναι οι (4.78) οι οποίες τώρα γράφονται
| (4.85) |
Αν θεωρήσουμε μία συνολική μετατόπιση των δινών κατά διάνυσμα , δηλαδή θεωρήσουμε ότι οι θέσεις των δινών γίνονται τότε έχουμε ότι
| (4.86) |
όπου έχουμε χρησιμοποιήσει τον συμβολισμό για τη συνολική ισχύ του συστήματος των δινών. Στην περίπτωση είναι σαφές ότι μία συνολική μετατόπιση του συστήματος δεν μπορεί να υπάρξει, αφού τότε θα παραβιάζονταν οι νόμοι διατήρησης (4.85). Ώστε, αυτό που περιμένουμε από το τρίγωνο των δινών είναι να περιστρέφεται γύρω από μία σταθερή θέση. Στην περίπτωση όμως μία μετατόπιση του συστήματος των δινών δεν αποκλείεται. Μάλιστα, αυτό πραγματικά συμβαίνει λόγω της αλληλεπίδρασης μεταξύ τους. Η περιγραφή της δυναμικής για τις τρεις δίνες που μόλις δώσαμε βρίσκεται σε πλήρη αναλογία με την περιστροφική κίνηση δύο δινών με και τη μεταφορική κίνησή τους στην περίπτωση που είδαμε σε προηγούμενη παράγραφο. Βέβαια, για την επιβεβαίωση των παραπάνω θα πρέπει να λύσουμε το πλήρες σύστημα των εξισώσεων (4.80) είτε αναλυτικά είτε αριθμητικά.
4.2.7 Χαμιλτονιανή περιγραφή
Αν θεωρήσουμε την ενέργεια αλληλεπίδρασης των δινών (4.76) παρατηρούμε ότι οι εξισώσεις κίνησης (4.77) μπορούν να γραφούν στη μορφή
| (4.87) |
Αυτή μπορεί να θεωρηθεί ως η χαμιλτονιανή μορφή των εξισώσεων κίνησης αν θεωρήσουμε ως ζεύγη κανονικών μεταβλητών τα .
Μπορούμε να δούμε ότι, σε συμφωνία με τον χαμιλτονιανό φορμαλισμό, το σύστημα έχει ως διατηρήσιμες ποσότητες την ολική γραμμική ορμή
| (4.88) |
και την ολική στροφορμή (4.79).
4.2.8 Λαγκρανζιανή περιγραφή
Η Λαγκρανζιανή για ένα σύστημα δινών μπορεί να γραφεί ως εξής
| (4.89) |
Μπορούμε να επιβεβαιώσουμε ότι αυτή η Λαγκρανζιανή περιγράφει το σύστημα δινών αφού μπορούμε να εξαγάγουμε τις εξισώσεις κίνησης ως τις εξισώσεις Euler-Lagrange για την παραπάνω Λαγκρανζιανή:
| (4.90) |
Επίσης μπορούμε να εξαγάγουμε από τον γενικό τύπο της λαγκρανζιανής μηχανικής την ενέργεια, η οποία προκύπτει να είναι η Χαμιλτονιανή (4.76) του συστήματος.
Η Λαγκρανζιανή για την περιγραφή δινών (4.89) έχει σημαντικές ομοιότητες με τη Λαγκρανζιανή για την περιγραφή κίνησης φορτίων σε ηλεκτρικό και μαγνητικό πεδίο στην Εξ. (4.31). Ο κινητικός όρος της Εξ. (4.31) όμως λείπει στην Εξ. (4.31). Θα μπορούσε λοιπόν κανείς να πάρει τη Λαγκρανζιανή για τις δίνες από αυτή για τα φορτία θέτοντας τη μάζα να είναι μηδέν. Στη Λαγκρανζιανή (4.89) έχουμε περιλάβει έναν όρο που περιγράφει αλληλεπίδραση μεταξύ των δινών. Ένα εξωτερικό δυναμικό το οποίο θα επιδρούσε στις δίνες θα μπορούσε να προστεθεί στη Λαγκρανζιανή με τρόπο ανάλογο του δυναμικού αλληλεπίδρασης.
Παρατήρηση 4.15.
Η ισχύς της δίνης έχει τώρα τον ρόλο που είχε το γινόμενο (φορτίο επί μαγνητικό πεδίο) στην περίπτωση των φορτίων.