3 Δυναμικά συστήματα 3.1 Συστήματα διαφορικών εξισώσεων πρώτης τάξης 3.3 Μη γραμμικά συστήματα

3.2 Διαφορικές εξισώσεις δεύτερης τάξης

3.2.1 Το απλό εκκρεμές

Ένα σώμα μάζας $m$ το οποίο εξαρτάται από αβαρή ράβδο μήκους $\ell$ και κινείται υπό την επίδραση της δύναμης βαρύτητας το ονομάζουμε απλό εκκρεμές. Αν ονομάσουμε $\theta$ τη γωνία της ράβδου από την κατακόρυφο τότε η εξίσωση κίνησης για το εκκρεμές είναι [17]

m\ell^{2}\,\ddot{\theta}+mg\ell\,\sin\theta=0,

(3.46)

όπου $g$ είναι η επιτάχυνση της βαρύτητας. Πρόκειται για μία διαφορική εξίσωση δεύτερης τάξης. Αυτή είναι μάλιστα μία μη-γραμμική εξίσωση διότι περιέχει το $\sin\theta$ .

Παρατηρούμε ότι

\ddot{\theta}=\frac{d\dot{\theta}}{dt}=\frac{d\dot{\theta}}{d\theta}\,\frac{d% \theta}{dt}=\frac{d\dot{\theta}}{d\theta}\,\dot{\theta}

και γράφουμε την εξίσωση (3.46) ως

m\ell^{2}\,\dot{\theta}\,\frac{d\dot{\theta}}{d\theta}+mg\ell\,\sin\theta=0.

Έτσι, ενώ είχαμε εξίσωση για τη μεταβλητή $\theta=\theta(t)$ , τώρα έχουμε περάσει σε μιά εξίσωση για την ταχύτητα $\dot{\theta}$ ως συνάρτηση του $\theta$ . Ολοκληρώνουμε την τελευταία εξίσωση

m\ell^{2}\int{\dot{\theta}\,d\dot{\theta}}+mg\ell\int{\sin\theta\,d\theta}=0

και βρίσκουμε

\frac{1}{2}\,m\ell^{2}\,\dot{\theta}^{2}-mg\ell\,\cos\theta=C,

(3.47)

το οποίο είναι ολοκλήρωμα της κίνησης (είναι μάλιστα το ολοκλήρωμα της ενέργειας). Η τιμή της $C$ μπορεί να καθορισθεί εάν, π.χ., υποθέσουμε κάποιες αρχικές συνθήκες $\theta_{0}=\theta(t=0),\;\dot{\theta}_{0}=\dot{\theta}(t=0)$ τις οποίες θα αντικαταστήσουμε στο αριστερό μέλος της παραπάνω εξίσωσης ώστε θα υπολογίσουμε τη $C$ . Είναι προφανές ότι για κάθε ζευγάρι αρχικών συνθηκών θα βρίσκουμε, εν γένει, διαφορετική σταθερά $C$ , δηλαδή, κάθε τιμή της $C$ αντιστοιχεί σε διαφορετικές λύσεις του προβλήματος.

Για να βρούμε λύση της εξίσωσης κίνησης (3.46) χρειαζόμαστε τις τιμές της γωνίας $\theta$ και της ταχύτητας $\dot{\theta}$ ως αρχικές συνθήκες. Άρα η κατάσταση του εκκρεμούς καθορίζεται από τις τιμές του ζεύγους $\theta,\dot{\theta}$ . Θα ορίζουμε το επίπεδο των $(\theta,\dot{\theta})$ στον οποίο μπορούμε να καθορίσουμε τις καταστάσεις του εκκρεμούς και να περιγράψουμε την κίνησή του. Αυτός είναι ο χώρος φάσεων για το εκκρεμές.

Παρατηρούμε ότι το ολοκλήρωμα (3.47) δίνει εξισώσεις καμπυλών στον χώρο φάσεων. Κάθε καμπύλη σε αυτό το διάγραμμα περιγράφει μία πιθανή κίνηση του συστήματος στον χώρο των καταστάσεων του.

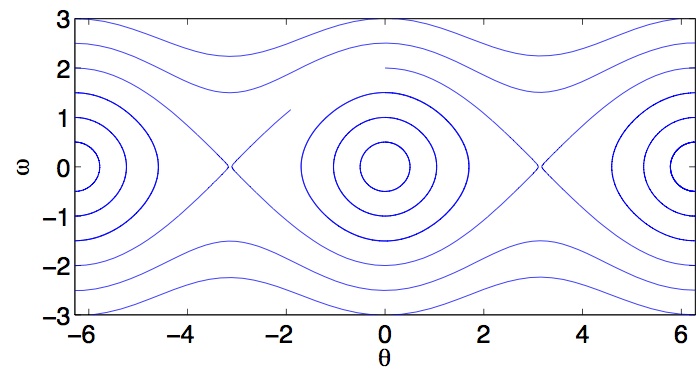
Σχήμα 3.4: Διάγραμμα φάσεων για το απλό εκκρεμές.

Ας γράψουμε την Εξ. (3.47) σε μία πιο απλή μορφή αφού διαιρέσουμε με $m\ell^{2}$ :

\frac{1}{2}\,\dot{\theta}^{2}-\omega^{2}\,\cos\theta=c,

(3.48)

όπου θέσαμε $\omega^{2}=g/\ell$ και $c$ είναι μία νέα σταθερά. Παρατηρούμε ότι η Εξ. (3.48) δίνει $c\geq-\omega^{2}\cos\theta$ . Άρα η σταθερά $c$ παίρνει τιμές $c\geq-\omega^{2}$ και η διερεύνηση του διαγράμματος φάσεων μπορεί να περιορισθεί στις αποδεκτές τιμές του $c$ .

Σημεία ισορροπίας

Θεωρούμε $c=-\omega^{2}$ , οπότε η εξίσωση (3.47) ικανοποιείται μόνο για ταχύτητα $\dot{\theta}=0$ , και για τις γωνίες $\theta=0,\pm 2\pi,\ldots$ . Αυτές οι τιμές παριστάνονται με μεμονωμένα σημεία στο διάγραμμα φάσεων, ενώ οι αντίστοιχες λύσεις των εξισώσεων (3.46) είναι οι σταθερές συναρτήσεις $\theta(t)=0,\pm 2\pi,\ldots$ . Τα αντίστοιχα σημεία ισορροπίας στο διάγραμμα φάσεων είναι $(\theta,\dot{\theta})=(0,0),(\pm 2\pi,0)$ κλπ.

Θεωρούμε επίσης την περίπτωση $c=\omega^{2}$ . Η εξίσωση (3.47) ικανοποιείται για $\dot{\theta}=0$ , και $\theta=\pm\pi,\pm 3\pi,\ldots$ . Επιπλέον η εξίσωση κίνησης (3.46) δίνει $\ddot{\theta}=0$ για αυτές τις τιμές του $\theta$ , συνεπώς έχουμε λύσεις τις σταθερές συναρτήσεις $\theta(t)=\pm\pi,\pm 3\pi,\ldots$ . Τα αντίστοιχα σημεία ισορροπίας στο διάγραμμα φάσεων είναι $(\theta,\dot{\theta})=(\pm\pi,0)$ κλπ.

Τα σημεία ισορροπίας του χώρου φάσεων αντιστοιχούν σε θέσεις για τις οποίες το εκκρεμές παραμένει ακίνητο, εφόσον η αρχική του ταχύτητα είναι $\dot{\theta}=0$ .

Σαγματικά σημεία

Στην περίπτωση κατά την οποία η σταθερά $c$ πάρει τιμή $c\approx\omega^{2}$ βρισκόμαστε κοντά σε ένα από τα σημεία ισορροπίας $(\pm\pi,0)$ . Ας επιλέξουμε την περίπτωση $\theta\approx\pi$ , οπότε μπορούμε να γράψουμε την προσέγγιση

\cos\theta\approx\cos\pi-(\cos\theta)^{\prime}_{\theta=\pi}(\theta-\pi)+(\cos% \theta)^{\prime}_{\theta=\pi}(\theta-\pi)^{2}/2=-1+(\theta-\pi)^{2}/2.

Εισάγωντας την προσέγγιση στην (3.48) παίρνουμε

\frac{1}{2}\dot{\theta}^{2}-\omega^{2}\left(-1+\frac{(\theta-\pi)^{2}}{2}% \right)=c\Rightarrow\dot{\theta}^{2}-\omega\,(\theta-\pi)^{2}=c^{\prime},

(3.49)

όπου $c^{\prime}$ είναι μία νέα σταθερά. Ας ορίσουμε νέα μεταβλητή για την απόκλιση της γωνίας από τη θέση ισορροπίας $\theta_{1}:=\theta-\pi$ . Τότε για καμπύλες κοντά στο σημείο $(\pi,0)$ έχουμε την εξίσωση

\dot{\theta}_{1}^{2}-\omega^{2}\,\theta_{1}^{2}=c^{\prime}

η οποία περιγράφει μία οικογένεια υπερβολών στο διάγραμμα φάσεων. Οι ασύμπτωτες των υπερβολών αυτών τέμνονται στο σημείο ισορροπίας $(\theta,\dot{\theta})=(\pi,0)$ . Παρόμοιο αποτέλεσμα έχουμε και για το σημείο $(\theta,\dot{\theta})=(-\pi,0)$ . Τα σημεία $(\pm\pi,0)$ τα οποία περιβάλλονται από τις υπερβολές είναι σαγματικά σημεία ισορροπίας και θα μελετηθούν αναλυτικότερα στη συνέχεια.

Περιοδική κίνηση

Στην περίπτωση κατά την οποία η σταθερά $c$ πάρει τιμή $c\approx-\omega^{2}$ με $c>-\omega^{2}$ , μπορούμε να γράψουμε $\cos\theta\approx 1-\theta^{2}/2$ ώστε η (3.48) γράφεται

\frac{1}{2}\dot{\theta}^{2}-\omega^{2}\left(1-\frac{\theta^{2}}{2}\right)=c% \Rightarrow\dot{\theta}^{2}+\omega^{2}\,\theta^{2}=c^{\prime},

(3.50)

όπου $c^{\prime}$ είναι μία νέα σταθερά. Η τελευταία εξίσωση δίνει μία οικογένεια ελλείψεων στο διάγραμμα φάσεων, οι οποίες περιβάλλουν το σημείο ισορροπίας $(\theta,\dot{\theta})=(0,0)$ . Για κάθε $c^{\prime}>0$ έχουμε μία έλλειψη, ενώ για $c^{\prime}=0$ βρίσκουμε το ίδιο το σημείο ισορροπίας. Μπορούμε να επαναλάβουμε τον παραπάνω υπολογισμό για κάθε ένα από τα σημεία $(\theta,\dot{\theta})=(\pm 2\pi,0),(\pm 4\pi,0)$ κλπ, με παρόμοια αποτελέσματα. Αυτά τα σημεία ισορροπίας είναι κέντρα.

Περιστροφική κίνηση

Ας δούμε τώρα την περίπτωση $c>\omega^{2}$ , οπότε η Εξ. (3.48) δίνει $\dot{\theta}^{2}>0$ . Αυτό σημαίνει $\dot{\theta}\neq 0$ και άρα το $\theta$ είναι μία μονότονη συνάρτηση του χρόνου. Για $\dot{\theta}>0$ παίρνουμε μη-κλειστές καμπύλες με φορά από αρνητικά $\theta$ προς θετικά, ενώ για $\dot{\theta}<0$ παίρνουμε αντίστοιχες καμπύλες με αντίθετη φορά. Οι καμπύλες αυτές αντιστοιχούν σε συνεχή περιστροφική κίνηση του εκκρεμούς.

3.2.2 Εξισώσεις δεύτερης τάξης ως σύστημα εξισώσεων πρώτης τάξης

Γενικεύουμε την περίπτωση του προηγουμένου παραδείγματος και υποθέτουμε την εξίσωση δεύτερης τάξης [17]

\ddot{x}=f(x,\dot{x})

(3.51)

η οποία περιγράφει, π.χ., την κίνηση ενός μηχανικού συστήματος. Η κατάσταση του συστήματος καθορίζεται από τις τιμές των $x,\dot{x}$ . Για να λύσουμε την εξίσωση (το πρόβλημα αρχικών τιμών) χρειαζόμαστε τις τιμές των μεταβλητών σε κάποια χρονική στιγμή $[x(t_{0}),\dot{x}(t_{0})]$ . Αυτό δίνει την αφορμή να γράψουμε την παραπάνω εξίσωση σε μία νέα μορφή όπου τα $x$ και $\dot{x}$ θα εμφανίζονται σαν ανεξάρτητες μεταβλητές. Δίνουμε ένα νέο όνομα στο $\dot{x}$ :

\dot{x}=y

(3.52)

και η αρχική εξίσωση γράφεται

\dot{y}=f(x,y).

(3.53)

Οι δύο τελευταίες αποτελούν ένα σύστημα δύο εξισώσεων πρώτης τάξης το οποίο είναι ισοδύναμο με την αρχική εξίσωση δεύτερης τάξης.

Το διάγραμμα φάσεων του συστήματος των εξισώσεων βρίσκεται στο επίπεδο $(x,y)$ . Οι καμπύλες του διαγράμματος φάσεων ικανοποιούν την εξίσωση

\frac{dy}{dx}=\frac{f(x,y)}{y}

(3.54)

όπως προκύπτει και από την Εξ. (3.9). Η εξίσωση αυτή μπορεί κατ’ αρχήν να δώσει λύσεις $y=y(x)$ οι οποίες ορίζουν τις καμπύλες του διαγράμματος φάσεων στο επίπεδο $(x,y)$ .

Παράδειγμα 3.10.

Μελετήστε και σχεδιάστε το διάγραμμα φάσεων για την εξίσωση $\ddot{x}+a\sin x=0$ .

Επίλυση.

Αυτή είναι η εξίσωση για το απλό εκκρεμές. Γράφουμε

\dot{x}=y,\qquad\dot{y}=-a\sin x.

Τα σημεία ισορροπίας βρίσκονται αν θέσουμε $\dot{x}=0,\;\dot{y}=0$ και λύσουμε το αλγεβρικό σύστημα που προκύπτει:

y=0\qquad-a\sin x=0.

Οι λύσεις είναι $y=0,\;x=0,\pm\pi,\pm 2\pi,\ldots$ . Παρατηρήστε ότι όλα τα σημεία ισορροπίας βρίσκονται επάνω στον άξονα $x$ .

Οι καμπύλες του διαγράμματος φάσεων δίνονται από την

\frac{dy}{dx}=-\frac{a\sin x}{y}\Rightarrow\int{y\,dy}=-a\int{\sin x\,dx}% \Rightarrow\frac{1}{2}\,y^{2}-a\cos x=C.

Για κάθε τιμή της παραμέτρου $C$ παίρνουμε μία καμπύλη στο διάγραμμα φάσεων (Σχήμα 3.4).

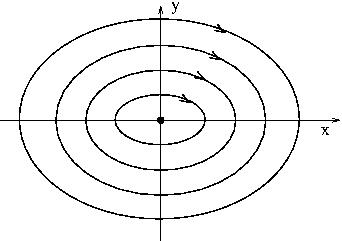
Σχήμα 3.5: Διάγραμμα φάσεων για ένα κέντρο στην αρχή των αξόνων.

Παράδειγμα 3.11.

Μελετήστε και σχεδιάστε το διάγραμμα φάσεων για την εξίσωση $\ddot{x}+\omega^{2}x=0$ .

Επίλυση.

Αυτή είναι η εξίσωση για τον αρμονικό ταλαντωτή. Γράφουμε

\dot{x}=y,\qquad\dot{y}=-\omega^{2}x.

Το σύστημα έχει ένα σημείο ισορροπίας το οποίο βρίσκεται αν θέσουμε $\dot{x}=0,\;\dot{y}=0\Rightarrow(x,y)=(0,0)$ . Οι καμπύλες του διαγράμματος φάσεων δίνονται από την

\frac{dy}{dx}=-\frac{\omega^{2}x}{y}\Rightarrow\int{y\,dy}+\int{\omega^{2}x\,% dx}=0\Rightarrow y^{2}+\omega^{2}x=C.

Για κάθε τιμή της παραμέτρου $C$ παίρνουμε μία καμπύλη, η οποία είναι έλλειψη. Οι ελλείψεις περιβάλλουν το σημείο ισορροπίας (0,0) (Σχήμα 3.5).

Παράδειγμα 3.12.

Μελετήστε το διάγραμμα φάσεων για την εξίσωση $\ddot{x}-\omega^{2}x=0$ .

Επίλυση.

Γράφουμε

\dot{x}=y,\qquad\dot{y}=\omega^{2}x.

\frac{dy}{dx}=\frac{\omega^{2}x}{y}\Rightarrow\int{y\,dy}-\int{\omega^{2}x\,dx% }=0\Rightarrow y^{2}-\omega^{2}x^{2}=C.

Για κάθε τιμή της παραμέτρου $C\neq 0$ παίρνουμε μία καμπύλη, η οποία είναι υπερβολή, στο διάγραμμα φάσεων Για $C=0$ παίρνουμε ευθείες ( $y=\pm\omega x$ ) που παριστάνουν φασικές καμπύλες οι οποίες τέμνονται στο σημείο ισορροπίας (0,0).