3 Δυναμικά συστήματα 3 Δυναμικά συστήματα 3.2 Διαφορικές εξισώσεις δεύτερης τάξης

3.1 Συστήματα διαφορικών εξισώσεων πρώτης τάξης

Παρακάτω θα δούμε μια βασική εισαγωγή σε συστήματα διαφορικών εξισώσεων και στα δυναμικά συστήματα [15, 17, 29, 13, 35, 39]

3.1.1 Χώρος φάσεων

Στη μελέτη μεταβολής του πληθυσμού για κάποιο βιολογικό είδος θεωρούμε, στην απλούστερη περίπτωση, ότι η αύξησή του είναι ανάλογη του ήδη υπάρχοντος πληθυσμού. Αν θέσουμε $x=x(t)$ τον πληθυσμό, τότε η διαφορική εξίσωση που προκύπτει είναι

\dot{x}=ax,

(3.1)

όπου $a$ είναι μία σταθερά η οποία εξαρτάται από τον ρυθμό των γεννήσεων αλλά και των θανάτων, όπως θα δούμε στο κεφάλαιο 5. Η Εξ. (3.1) είναι μία γραμμική διαφορική εξίσωση πρώτης τάξης και έχει τη λύση $x(t)=x_{0}\,e^{at}$ , όπου $x_{0}$ είναι μία σταθερά. Ισχύει $x(t=0)=x_{0}$ , άρα η $x_{0}$ δίνει τον πληθυσμό του είδους στον αρχικό χρόνο της μελέτης.

Θα προχωρήσουμε στη μελέτη διαφορικών εξισώσεων για δύο μεταβλητές $x, y$ , οι οποίες θα μπορούσαν να παριστάνουν τους πληθυσμούς δύο διαφορετικών ειδών στη Βιολογία, είτε τη συγκέντρωση δύο διαφορετικών χημικών στοιχείων, είτε οικονομικά μεγέθη κλπ. Για κάθε μεταβλητή θα έχουμε μία διαφορική εξίσωση η οποία περιγράφει τη μεταβολή της στον χρόνο, δηλαδή, τη δυναμική της. Ένα απλό σύστημα εξισώσεων είναι το ακόλουθο

\frac{dx}{dt}=by,\qquad\frac{dy}{dt}=-ax,\qquad a,b>0.

(3.2)

Πρόκειται για ένα γραμμικό σύστημα και άρα μπορούμε να πούμε ότι είναι μία γενίκευση του (3.1). Η λύσεις του συστήματος θα είναι στη μορφή $x=x(t),\;y=y(t)$ και δίνουν, π.χ., τους πληθυσμούς δύο ειδών σαν συνάρτηση του χρόνου. Παρατηρούμε ότι το σύστημα των εξισώσεων (3.2) έχει μία ιδιαίτερα απλή λύση την οποία βρίσκουμε αν ζητήσουμε $\dot{x}=0,\,\dot{y}=0$ . Για μία τέτοια λύση τα δεξιά μέλη των δύο εξισώσεων πρέπει να μηδενίζονται, άρα η λύση είναι η

x(t)=0,\qquad y(t)=0.

(3.3)

Πρόκειται για μία σταθερή λύση και γι’ αυτό το $(x,y)=(0,0)$ το ονομάζουμε σημείο ισορροπίας του συστήματος. Το όνομα εκφράζει την ιδιότητα ότι ένα σύστημα με αρχική συνθήκη στο σημείο ισορροπίας παραμένει σε αυτό το σημείο για κάθε χρόνο.

Αν δεν βρισκόμαστε στην κατάσταση εκείνη η οποία είναι σημείο ισορροπίας του συστήματος τότε βέβαια οι πληθυσμοί θα εξελίσσονται στον χρόνο και για κάθε χρονική στιγμή $t$ θα έχουμε μία κατάσταση του συστήματος η οποία περιγράφεται από τις τιμές των μεταβλητών $(x(t),y(t))$ . Κάθε τέτοια κατάσταση παριστάνεται στο επίπεδο $x y$ από ένα σημείο [15, 17].

Παρατήρηση 3.1.

Ονομάζουμε το επίπεδο $x y$ , στο οποίο μπορούν να παρασταθούν όλες οι δυνατές καταστάσεις του συστήματος, χώρο των φάσεων.

Για την περίπτωση πληθυσμιακών μοντέλων, ένα σημείο στο χώρο φάσεων περιγράφει έναν συγκεκριμένο συνδυασμό πληθυσμών. Η περιγραφή του συστήματος με σημεία στον χώρο φάσεων είναι χρήσιμη όταν ενδιαφερόμαστε για τη σχέση της μίας μεταβλητής με την άλλη αφήνοντας σε δεύτερη μοίρα την ακριβή εξέλιξη της καθεμίας με τον χρόνο. Είναι απλό να φανταστούμε ότι με την εξέλιξη του χρόνου $t$ το αντίστοιχο σημείο $(x(t),y(t))$ διαγράφει μία καμπύλη στο χώρο των φάσεων. Μάλιστα, το διάνυσμα $(x(t),y(t))$ δίνει την παραμετρική αναπαράσταση αυτής της καμπύλης.

Γενικότερα, οι λύσεις του συστήματος των εξισώσεων περιγράφονται από οικογένειες καμπυλών στον χώρο των φάσεων. Μπορούμε να εξαγάγουμε μία εξίσωση για τις καμπύλες. Ας θεωρήσουμε τα σημεία στα οποία η παράγωγος $dx/dt(t)\neq 0$ , τότε μπορούμε να αντιστρέψουμε τη συνάρτηση και να πάρουμε $t=t(x)$ σε περιοχή γύρω από αυτά τα σημεία. Ώστε θα έχουμε τις καμπύλες $y=y(t(x))$ . Ο κανόνας της αλυσίδας μας δίνει

\frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}\frac{dy/dt}{dx/dt}.

(3.4)

Κάτι ανάλογο μπορούμε να κάνουμε και στα σημεία στα οποία $\dot{y}(t)\neq 0$ .

Παράδειγμα 3.1.

Θεωρούμε το σύστημα

\frac{dx}{dt}=y,\qquad\frac{dy}{dt}=-ax,\qquad a>0.

Οι καμπύλες του διαγράμματος φάσεων βρίσκονται από την εξίσωση

\frac{dy}{dx}=-\frac{ax}{y},

η οποία λύνεται με χωρισμό μεταβλητών:

\int y\,dy=-\int ax\,dx\Rightarrow ax^{2}+y^{2}=C.

(3.5)

To $C$ μπορεί να πάρει, κατ’ αρχήν, οποιαδήποτε τιμή. Για $C=0$ η Εξ. (3.5) ικανοποιείται μόνο για το σημείο ισορροπίας $(0,0)$ . Για κάθε τιμή $C>0$ παίρνουμε ελλείψεις που περικλείουν το σημείο ισορροπίας. Άρα, λέμε ότι οι καμπύλες του διαγράμματος φάσεων είναι ελλείψεις. Τέλος, για $C<0$ η Εξ. (3.5) δεν ικανοποιείται για κανένα σημείο $(x,y)$ , ώστε δεν παίρνουμε καμπύλες στον χώρο φάσεων για αυτές τις τιμές του $C$ .

Παράδειγμα 3.2.

Θεωρούμε το σύστημα

\frac{dx}{dt}=y,\qquad\frac{dy}{dt}=ax,\qquad a>0.

Οι καμπύλες του διαγράμματος φάσεων βρίσκονται από την

\frac{dy}{dx}=-\frac{ax}{y}\Rightarrow\int y\,dy=\int ax\,dx\Rightarrow ax^{2}% -y^{2}=C.

Για κάθε τιμή $C>0$ παίρνουμε υπερβολές οι οποίες τέμνουν τον άξονα $x$ . Για κάθε τιμή $C<0$ παίρνουμε υπερβολές οι οποίες τέμνουν τον άξονα $y$ . Τέλος για $C=0$ η Εξ. (3.5) δίνει $y=\pm\sqrt{a}\,x$ , δηλαδή δύο ευθείες οι οποίες τέμνονται στο σημείο ισορροπίας $(0,0)$ .

Συστήματα δύο διαφορικών εξισώσεων πρώτης τάξης

Τα συστήματα τα οποία έχουμε μελετήσαμε στα παραπάνω παραδείγματα είναι συστήματα δύο διαφορικών εξισώσεων πρώτης τάξης. Η γενική μορφή συστήματος δύο συνήθων διαφορικών εξισώσεων πρώτης τάξης είναι [13, 39]

\begin{split}\displaystyle\dot{x}&\displaystyle=X(x,y)\\ \displaystyle\dot{y}&\displaystyle=Y(x,y).\end{split}

(3.6)

Παρατήρηση 3.2.

Ονομάζουμε λύσεις του συστήματος (3.6) τα ζεύγη συναρτήσεων

x=x(t),\qquad y=y(t).

(3.7)

για τα οποία ικανοποιούνται οι εξ. (3.6).

Παρατήρηση 3.3.

(Σημεία ισορροπίας) Τα σημεία ισορροπίας του συστήματος είναι εκείνα για τα οποία ισχύουν οι

X(x,y)=0,\qquad Y(x,y)=0.

(3.8)

Για τις λύσεις $(x,y)=(x^{*},y^{*})$ των αλγεβρικών εξισώσεων (3.8) έχουμε από το σύστημα (3.6) ότι $\dot{x}=0,\,\dot{y}=0$ , δηλαδή οι $x(t)=x^{*},\,y(t)=y^{*}$ είναι λύσεις του συστήματος οι οποίες είναι σταθερές στον χρόνο [15, 17].

Παρατήρηση 3.4.

(Διάγραμμα φάσεων) Οι λύσεις $x(t),y(t)$ του συστήματος (3.6) παριστάνονται με καμπύλες στον χώρο των μεταβλητών $(x,y)$ , δηλαδή στο επίπεδο $x y$ . Ο χώρος αυτός λέγεται χώρος φάσεων. Η εξίσωση των καμπυλών είναι

\frac{dy}{dx}=\frac{Y(x,y)}{X(x,y)}.

(3.9)

Tο σύνολο των καμπυλών λέγεται διάγραμμα φάσεων.

3.1.2 Συστήματα γραμμικών διαφορικών εξισώσεων με δύο μεταβλητές

Ένα γραμμικό σύστημα με δύο μεταβλητές έχει τη γενική μορφή [15, 17, 29, 35]

\begin{split}\displaystyle\dot{x}&\displaystyle=ax+by\\ \displaystyle\dot{y}&\displaystyle=cx+dy.\end{split}

(3.10)

Το σημείο ισορροπίας βρίσκεται από τις αλγεβρικές σχέσεις που προκύπτουν αν μηδενίσουμε τα δεξιά μέλη των εξισώσεων:

\begin{cases}ax+by&=0\\ cx+dy&=0\end{cases}\Rightarrow\begin{cases}x&=0\\ y&=0.\end{cases}

(3.11)

Η λύση που βρήκαμε είναι μοναδική εκτός εάν η ορίζουσα των συντελεστών του συστήματος εξισώσεων είναι μηδέν.

Παρατήρηση 3.5.

Για το σύστημα γραμμικών εξισώσεων (3.10) έχουμε ένα και μοναδικό σημείο ισορροπίας στην αρχή των αξόνων $(x,y)=(0,0)$ εάν $ad-bc\neq 0$ .

Βρίσκουμε λύσεις των Εξ. (3.10) θεωρώντας την εκθετική συνάρτηση

x(t)=r\,e^{\lambda t},\quad y(t)=s\,e^{\lambda t},

(3.12)

όπου $r,s,\lambda$ είναι σταθερές. Αντικατάσταση των (3.12) στις (3.10) δίνει το γραμμικό σύστημα αλγεβρικών εξισώσεων

\begin{split}&\displaystyle(a-\lambda)r+bs=0\\ &\displaystyle cr+(d-\lambda)s=0.\end{split}

(3.13)

Θεωρούμε ως αγνώστους τους $r, s$ και ζητάμε να μηδενίζεται η ορίζουσα του συστήματος, ώστε το σύστημα να έχει λύσεις πέραν της τετριμμένης $(r,s)=(0,0)$ . H συνθήκη είναι

\left|\begin{array}[]{cc}a-\lambda&b\\ c&d-\lambda\end{array}\right|\Rightarrow\lambda^{2}-(a+d)\lambda+(ad-bc)=0.

(3.14)

Η τελευταία λέγεται χαρακτηριστική εξίσωση του συστήματος και στην περίπτωση μας έχει δύο λύσεις $\lambda_{1},\lambda_{2}$ . Για κάθε τιμή του $\lambda$ οι εξισώσεις (3.13) δίνουν τη σχέση μεταξύ $r$ και $s$ . Θα θέσουμε $(r_{1},s_{1})$ τη λύση του (3.13) για $\lambda=\lambda_{1}$ και αντιστοίχως, $(r_{2},s_{2})$ για $\lambda=\lambda_{2}$ .

Η γραμμικότητα του συστήματος (3.10) μας εξασφαλίζει ότι ο γραμμικός συνδυασμός δύο λύσεων είναι επίσης λύση. Ώστε, η γενική λύση του συστήματος (3.10) είναι γραμμικός συνδυασμός των δύο λύσεων που βρήκαμε:

\begin{split}\displaystyle x(t)&\displaystyle=r_{1}\,e^{\lambda_{1}t}+r_{2}\,e% ^{\lambda_{2}t}\\ \displaystyle y(t)&\displaystyle=s_{1}\,e^{\lambda_{1}t}+s_{2}\,e^{\lambda_{2}% t}.\end{split}

(3.15)

Θα επαναλάβουμε τώρα την παραπάνω διαδικασία σε μια διαφορετική γλώσσα. Το γραμμικό σύστημα (3.10) γράφεται στη μορφή

\left[\begin{array}[]{c}\dot{x}\\ \dot{y}\end{array}\right]=\left[\begin{array}[]{cc}a&b\\ c&d\end{array}\right]\left[\begin{array}[]{c}x\\ y\end{array}\right].

(3.16)

Έχουμε το διάνυσμα των αγνώστων

\bm{x}=\left[\begin{array}[]{c}x\\ y\end{array}\right]

(3.17)

και τον πίνακα του συστήματος

\bm{A}=\left[\begin{array}[]{cc}a&b\\ c&d\end{array}\right].

(3.18)

Ώστε, το γραμμικό σύστημα γράφεται στη μορφή

\dot{\bm{x}}=\bm{A}\,\bm{x}.

(3.19)

Οι παραπάνω συμβολισμοί θα πρέπει να μας βοηθήσουν καθώς μας θυμίζουν μορφές γνωστές από τη γραμμική άλγεβρα.

Ας θεωρήσουμε τη μορφή (3.12) την οποία γράφουμε

\bm{x}(t)=e^{\lambda t}\,\bm{v},\qquad\bm{v}=\left[\begin{array}[]{c}r\\ s\end{array}\right],

(3.20)

όπου $\bm{v}$ είναι σταθερό διάνυσμα. Παρατηρούμε ότι

\dot{\bm{x}}=\frac{d}{dt}\left(e^{\lambda t}\bm{v}\right)=\lambda\,e^{\lambda t% }\bm{v}

(3.21)

και

\bm{A}\bm{x}=\bm{A}\left(e^{\lambda t}\bm{v}\right)=e^{\lambda t}\,\bm{A}\bm{v}.

(3.22)

Αντικατάσταση των δύο τελευταίων σχέσεων στην (3.19) δίνει το πρόβλημα ιδιοτιμών:

\bm{A}\bm{v}=\lambda\bm{v}\quad\hbox{ή}\quad\lambda\,\left[\begin{array}[]{c}r% \\ s\end{array}\right]=\left[\begin{array}[]{cc}a&b\\ c&d\end{array}\right]\left[\begin{array}[]{c}r\\ s\end{array}\right],

άρα, το $\lambda$ μπορεί να πάρει τις δύο τιμές οι οποίες είναι ιδιοτιμές του πίνακα $2\times 2$ του συστήματος $\bm{A}$ και τα $\bm{v}$ είναι τα αντίστοιχα ιδιοδιανύσματά του.

3.1.3 Πραγματικές ιδιοτιμές

Ας δούμε την περίπτωση που οι λύσεις της χαρακτηριστικής εξίσωσης είναι πραγματικές, δηλαδή, ο πίνακας του συστήματος έχει πραγματικές ιδιοτιμές.

Παράδειγμα 3.3.

(Σαγματικό σημείο) Έστω το γραμμικό σύστημα

\begin{split}\displaystyle\dot{x}&\displaystyle=-x-3y\\ \displaystyle\dot{y}&\displaystyle=2y.\end{split}

(3.23)

Βρείτε τα σημεία ισορροπιάς και τις λύσεις του συστήματος.

Επίλυση.

Βρίσκουμε λύσεις θεωρώντας τη μορφή

x(t)=r\,e^{\lambda t},\quad y(t)=s\,e^{\lambda t}.

Αντικαθιστούμε στο σύστημα εξισώσεων (3.23) και βρίσκουμε

(\lambda+1)\,r+3\,s=0,\qquad(\lambda-2)\,s=0.

H χαρακτηριστική εξίσωση του συστήματος είναι

(\lambda+1)(\lambda-2)=0\Rightarrow\lambda=-1,\;\lambda=2.

Για $\lambda=-1$ βρίσκουμε ιδιοδιάνυσμα $(r,s)=(1,0)$ και για $\lambda=2$ βρίσκουμε ιδιοδιάνυσμα $(r,s)=(1,-1)$ . Ας ονομάσουμε $\lambda_{1}=-1,\;\lambda_{2}=2$ και

\bm{v}_{1}=\left[\begin{array}[]{c}1\\ 0\end{array}\right],\qquad\bm{v}_{2}=\left[\begin{array}[]{c}1\\ -1\end{array}\right].

Η γενική λύση του συστήματος είναι

\bm{x}(t)=c_{1}\,e^{\lambda_{1}t}\,\bm{v}_{1}+c_{2}\,e^{\lambda_{2}t}\,\bm{v}_% {2}

και σε αναλυτικότερη μορφή:

\left[\begin{array}[]{c}x\\ y\end{array}\right]=c_{1}\,e^{\lambda_{1}t}\,\left[\begin{array}[]{c}1\\ 0\end{array}\right]+c_{2}\,e^{\lambda_{2}t}\,\left[\begin{array}[]{c}1\\ -1\end{array}\right]\Rightarrow\begin{cases}x(t)&=c_{1}\,e^{-t}+c_{2}\,e^{2t}% \\ y(t)&=-c_{2}\,e^{2t}\end{cases}

όπου $c_{1},c_{2}$ είναι σταθερές.

Μπορούμε να δούμε κάποιες ειδικές ενδιαφέρουσες λύσεις. Αν έχουμε αρχική συνθήκη $(x,y)(t=0)=(1,0)$ τότε βρίσκουμε τη λύση του συστήματος θέτοντας $c_{1}=1,c_{2}=0$ στη γενική λύση. Έχουμε ειδική λύση $(x,y)(t)=(1,0)e^{-t}$ , η οποία, πραγματικά, ικανοποιεί την αρχική συνθήκη. Με τον διανυσματικό συμβολισμό έχουμε ότι, για αρχική συνθήκη $\bm{x}(t=0)=\bm{v}_{1}$ έχουμε λύση $\bm{x}(t)=\bm{v}_{1}\,e^{-t}$ . Με παρόμοιο τρόπο βλέπουμε ότι για αρχική συνθήκη $\bm{x}(t=0)=\bm{v}_{2}$ έχουμε λύση $\bm{x}(t)=\bm{v}_{1}\,e^{-2t}$ .

Παρατήρηση 3.6.

Αν οι αρχικές συνθήκες $(x,y)(t=0)$ βρίσκονται σε μία από τις ευθείες που ορίζουν τα ιδιοδιανύσματα $\bm{v}_{1}$ ή $\bm{v}_{2}$ , τότε η λύση του συστήματος παραμένει επάνω στην ευθεία που ορίζει το αντίστοιχο ιδιοδιάνυσμα. Δηλαδή, οι ευθείες που ορίζουν τα ιδιοδιανύσματα αποτελούν κάποιες ειδικές περιοχές του χώρου φάσεων. Αυτές είναι αναλλοίωτοι υπόχωροι του χώρου φάσεων, δηλαδή, η κίνηση για όλους τους χρόνους $t$ περιορίζεται επάνω σε αυτούς του υποχώρους.

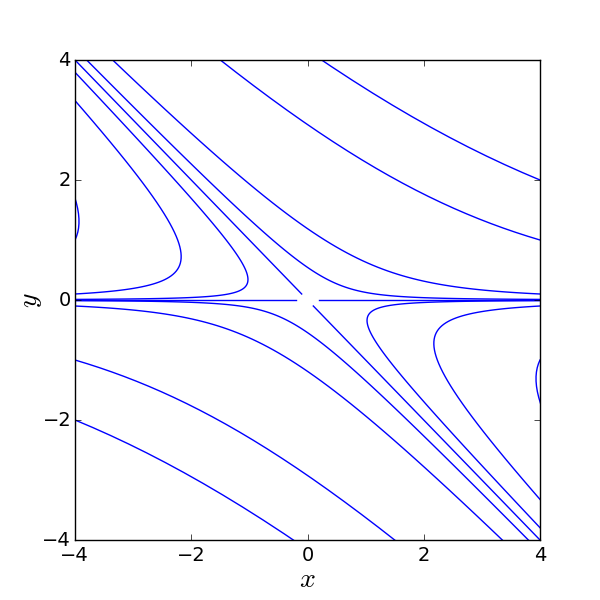
Σχήμα 3.1: Διάγραμμα φάσεων για το σύστημα (3.23). Το σημείο ισορροπίας στην αρχή των αξόνων είναι σαγματικό.

Όταν το σύστημα βρίσκεται στην ευθεία που ορίζει το $\bm{v}_{1}$ , το οποίο αντιστοιχεί σε αρνητική ιδιοτιμή $\lambda_{1}=-1$ , το σημείο $(x,y)(t)$ θα πλησιάζει την αρχή των αξόνων (το σημείο ισορροπίας) κινούμενο επάνω σε αυτή την ευθεία όταν ο χρόνος πηγαίνει στο άπειρο. Όταν το σύστημα βρίσκεται στην ευθεία του $\bm{v}_{2}$ , το οποίο αντιστοιχεί σε θετική ιδιοτιμή $\lambda_{1}=2$ , το σημείο $(x,y)(t)$ θα απομακρύνεται από την αρχή των αξόνων, κινούμενο επάνω σε αυτή την ευθεία, όταν ο χρόνος πηγαίνει προς το άπειρο.

Συμπεραίνουμε ότι οι ευθείες $c\bm{v}_{1}=c(1,0)$ και $c\bm{v}_{2}=c(1,-1)$ είναι δύο καμπύλες του χώρου φάσεων. Η φορά της κίνησης είναι προς την αρχή των αξόνων όταν κινούμαστε επάνω στην ευθεία $c(1,0)$ ενώ για την κίνηση στην ευθεία $c(-1,1)$ έχουμε απομάκρυνση από την αρχή των αξόνων.

Παρατήρηση 3.7.

Για ένα σύστημα με πραγματικές και αντίθετες ιδιοτιμές, οι ευθείες που ορίζονται από τα ιδιοδιανύσματα του πίνακα του συστήματος αποτελούν καμπύλες του χώρου φάσεων.

Μπορούμε να σχεδιάσουμε ποιοτικά όλες τις υπόλοιπες καμπύλες του διαγράμματος εάν σκεφτούμε ότι πρέπει να υπάρχει συνέχεια με τις δύο ευθείες των ιδιοδιανυσμάτων (δείτε Σχήμα 3.1).

Παρατήρηση 3.8.

Ένα σημείο ισορροπίας με δύο πραγματικές ετερόσημες ιδιοτιμές λέγεται σαγματικό σημείο (σάγμα) και είναι ένα ασταθές σημείο ισορροπίας.

Παράδειγμα 3.4.

(Κόμβος) Έστω το γραμμικό σύστημα

\begin{split}\displaystyle\dot{x}&\displaystyle=x-2y\\ \displaystyle\dot{y}&\displaystyle=3x-4y\end{split}

(3.24)

Βρείτε τα σημεία ισορροπίας και τις λύσεις του συστήματος. Σχεδιάστε το διάγραμμα φάσεων.

Επίλυση.

Η χαρακτηριστική εξίσωση είναι

\left|\begin{array}[]{cc}1-\lambda&-2\\ 3&-4-\lambda\end{array}\right|=0\Rightarrow\lambda^{2}+3\lambda+2=0,

με λύσεις $\lambda_{1}=-1,\;\lambda_{2}=-2$ και αντίστοιχα ιδιοδιανύσματα $\bm{v}_{1}=(1,1),\;\bm{v}_{2}=(2,3)$ . Η γενική λύση είναι

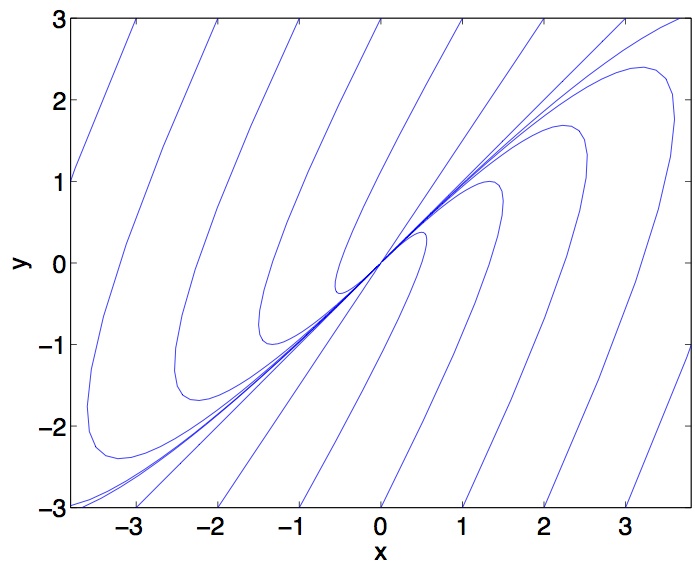
	$\displaystyle x(t)$	$\displaystyle=c_{1}\,e^{-t}+2c_{2}\,e^{-2t}$
	$\displaystyle y(t)$	$\displaystyle=c_{1}\,e^{-t}+3c_{2}\,e^{-2t}.$

Για να φθάσουμε στη σχεδίαση του διαγράμματος φάσεων ας μελετήσουμε πρώτα τα βασικά του χαρακτηριστικά. Παρατηρούμε ότι η γενική λύση δίνει, για κάθε $c_{1},c_{2}\in\mathbb{R}$ :

(x,y)\to(0,0),\qquad\hbox{όταν}\;t\to\infty

δηλαδή, η κατάσταση του συστήματος για μεγάλους χρόνους ( $t\to\infty$ ) τείνει, προς το σημείο ισορροπίας $(0,0)$ από οποιοδήποτε σημείο του χώρου φάσεων κι αν έχουμε ως αρχική συνθήκη. Βλέπουμε ότι όλες οι καμπύλες του διαγράμματος φάσεων καταλήγουν στην αρχή των αξόνων, δηλαδή, στο σημείο ισορροπίας.

Για να καταλάβουμε τα ποιοτικά χαρακτηριστικά των καμπυλών του διαγράμματος φάσεων σχηματίζουμε τον λόγο

\frac{x(t)}{y(t)}=\frac{c_{1}\,e^{-t}+2c_{2}\,e^{-2t}}{c_{1}\,e^{-t}+3c_{2}\,e% ^{-2t}}.

(3.25)

Μπορούμε να διαιρέσουμε αριθμητή και προνομαστή με $e^{-t}$ ώστε έχουμε

\frac{x(t)}{y(t)}=\frac{c_{1}+2c_{2}\,e^{-t}}{c_{1}+3c_{2}\,e^{-t}}.

(3.26)

Βλέπουμε ότι ισχύει

\frac{x(t)}{y(t)}=1,\qquad\hbox{για}\quad t\to\infty.

(3.27)

Άρα, αν σχεδιάσουμε μία οποιαδήποτε καμπύλη στο διάγραμμα φάσεων, αυτή θα πρέπει να πλησιάζει προς την αρχή των αξόνων (το σημείο ισορροπίας) κατά τη διεύθυνση της ευθείας $y=x$ . Αυτή είναι η διεύθυνση του διανύσματος $\bm{v}_{1}$ της μικρότερης (κατά απόλυτη τιμή) ιδιοτιμής. Ισοδύναμα, μπορούμε να πούμε ότι η ευθεία $y=x$ θα είναι εφαπτομένη κάθε καμπύλης του διαγράμματος φάσεων στο σημείο $(0,0)$ .

Ακολούθως, μπορούμε να διαιρέσουμε αριθμητή και προνομαστή στην Εξ. (3.25) με $e^{-2t}$ ώστε έχουμε

\frac{x(t)}{y(t)}=\frac{c_{1}\,e^{t}+2c_{2}}{c_{1}\,e^{t}+3c_{2}}.

(3.28)

Βλέπουμε ότι ισχύει

\frac{x(t)}{y(t)}=\frac{2}{3},\qquad\hbox{για}\quad t\to-\infty.

(3.29)

Άρα, η εφαπτομένη στις φασικές καμπύλες για χρόνους $t\to-\infty$ είναι παράλληλες στην ευθεία που ορίζει το ιδιοδιάνυσμα $\vec{v}_{2}=(2,3)$ της μεγαλύτερης (κατά απόλυτη τιμή) ιδιοτιμής.

Σχήμα 3.2: Διάγραμμα φάσεων για το σύστημα (3.24). Το σημείο ισορροπίας στην αρχή των αξόνων είναι κόμβος.

Το διάγραμμα φάσεων για το σύστημα (3.24) έχει σχεδιασθεί στο Σχ. 3.2 και μπορούμε να καταλάβουμε τα ποιοτικά χαρακτηριστικά των καμπυλών με βάση τις παραπάνω παρατηρήσεις.

Παρατήρηση 3.9.

Όλες οι φασικές καμπύλες για τον κόμβο του παραδείγματος είναι παράλληλες με την ευθεία που ορίζει το ιδιοδιάνυσμα $\bm{v}_{1}=(1,1)$ της μικρότερης (κατ΄ απόλυτη τιμή) ιδιοτιμής για μεγάλους χρόνους ( $t\to-\infty$ ), ενώ είναι παράλληλες με το ιδιοδιάνυσμα $\bm{v}_{2}=(2,3)$ της μεγαλύτερης (κατ΄ απόλυτη τιμή) ιδιοτιμής για χρόνους $t\to-\infty$ .

Παρατήρηση 3.10.

Ένα σημείο ισορροπίας με δύο πραγματικές ομόσημες ιδιοτιμές λέγεται κόμβος. Όταν οι ιδιοτιμές είναι αρνητικές (όπως στο προηγούμενο παράδειγμα) έχουμε έναν ευσταθή κόμβο. Στην αντίθετη περίπτωση (δύο θετικές ιδιοτιμές) ο κόμβος είναι ασταθής.

Διαγωνοποίηση πίνακα του συστήματος

Το σύστημα γραμμικών διαφορικών εξισώσεων (3.10) το οποίο μελετάμε μπορεί επίσης να γραφεί με τη βοήθεια πινάκων όπως είδαμε στην Εξ. (3.19), (την οποία επαναλαμβάνουμε εδώ για την πληρότητα της παραγράφου):

\dot{\bm{x}}=A\bm{x},

όπου o $\bm{x}$ είναι ο πίνακας των μεταβλητών ο οποίος ορίστηκε στην Εξ. (3.17) και $A$ είναι ο πίνακας $2\times 2$ του συστήματος (3.16) όπως ορίστηκε στην Εξ. (3.18). Θα προχωρήσουμε στη συνέχεια σε μελέτη του πίνακα $\bm{A}$ και για αυτό τον λόγο ανακαλούμε ένα σημαντικό θεώρημα της γραμμικής άλγεβρας [15, 29].

Θεώρημα.

Εάν οι ιδιοτιμές $\lambda_{1},\lambda_{2},\ldots,\lambda_{n}$ ενός πίνακα $\bm{A}$ διάστασεων $n\times n$ είναι πραγματικές και διάκριτες, τότε οποιoδήποτε σύνολο των αντίστοιχων ιδιοδιανυσμάτων $\{\bm{v}_{1},\bm{v}_{2},\ldots,\bm{v}_{n}\}$ είναι βάση του $\mathbb{R}^{n}$ . Ο πίνακας των ιδιοδιανυσμάτων $\bm{P}=[\bm{v}_{1},\bm{v}_{2},\ldots,\bm{v}_{n}]$ είναι αντιστρέψιμος και ισχύει

\bm{P}^{-1}\bm{A}\bm{P}={\rm diag}[\lambda_{1},\lambda_{2},\ldots,\lambda_{n}].

(3.30)

Για να βρούμε τη γενική λύση του γραμμικού συστήματος ορίζουμε ένα νέο διάνυσμα μεταβλητών

\bm{y}=\bm{P}^{-1}\bm{x},

(3.31)

για το οποίο έχουμε

\dot{\bm{y}}=\bm{P}^{-1}\dot{\bm{x}}=\bm{P}^{-1}\bm{A}\bm{x}=\bm{P}^{-1}\bm{A}% \bm{P}\bm{y}.

(3.32)

Εφαρμόζοντας το παραπάνω θεώρημα έχουμε

\dot{\bm{y}}={\rm diag}[\lambda_{1},\lambda_{2},\ldots,\lambda_{n}]\bm{y}.

(3.33)

Η γενική λύση του διαγώνιου αυτού συστήματος είναι

\bm{y}(t)={\rm diag}[e^{\lambda_{1}t},e^{\lambda_{2}t},\ldots,e^{\lambda_{n}t}% ]\,\bm{y}(0),

(3.34)

όπου $\bm{y}(0)$ είναι οι αρχικές συνθήκες εκφρασμένες στις μεταβλητές $\bm{y}$ . Τελικά, στις αρχικές μεταβλητές έχoυμε τη γενική λύση

\bm{x}(t)=\bm{P}\,{\rm diag}[e^{\lambda_{1}t},e^{\lambda_{2}t},\ldots,e^{% \lambda_{n}t}]\bm{P}^{-1}\bm{x}(0),

(3.35)

όπου $\bm{x}(0)$ είναι οι αρχικές συνθήκες.

Δεδομένου ότι συνήθως μελετάμε συστήματα δύο εξισώσεων είναι χρήσιμο να θυμηθούμε ότι για έναν $2\times 2$ πίνακα $\bm{P}$ ο αντίστροφος $\bm{P}^{-1}$ είναι

\bm{P}=\left[\begin{array}[]{cc}a&b\\ c&d\end{array}\right],\qquad\bm{P}^{-1}=\frac{1}{\Delta}\,\left[\begin{array}[% ]{cc}d&-b\\ -c&a\end{array}\right]

(3.36)

όπου $\Delta=ad-bc$ η διακρίνουσα του πίνακα $\bm{P}$ .

Παράδειγμα 3.5.

(Σαγματικό σημείο) Έστω το γραμμικό σύστημα

	$\displaystyle\dot{x}_{1}$	$\displaystyle=-x_{1}-3x_{2}$
	$\displaystyle\dot{x}_{2}$	$\displaystyle=2x_{2}$

Βρείτε τη γενική λύση του.

Επίλυση.

Ο πίνακας του συστήματος είναι

\bm{A}=\left[\begin{array}[]{cc}-1&-3\\ 0&2\end{array}\right].

Οι ιδιοτιμές του πίνακα είναι $\lambda_{1}=-1,\;\lambda_{2}=2$ άρα έχουμε ένα σαγματικό σημείο. Τα δύο αντίστοιχα ιδιοδιανύσματα είναι

\bm{v}_{1}=\left[\begin{array}[]{c}1\\ 0\end{array}\right],\qquad\bm{v}_{2}=\left[\begin{array}[]{c}-1\\ 1\end{array}\right].

Άρα έχουμε

\bm{P}=\left[\begin{array}[]{cc}1&-1\\ 0&1\end{array}\right],\qquad\bm{P}^{-1}=\left[\begin{array}[]{cc}1&1\\ 0&1\end{array}\right]

και

\bm{P}^{-1}\bm{A}\bm{P}=\left[\begin{array}[]{cc}-1&0\\ 0&2\end{array}\right].

Για τις μεταβλητές $\bm{y}=\bm{P}^{-1}\bm{x}$ έχουμε το σύστημα

	$\displaystyle\dot{y}_{1}$	$\displaystyle=-y_{1}$
	$\displaystyle\dot{y}_{2}$	$\displaystyle=2y_{2}.$

Η γενική λύση του είναι $y_{1}(t)=c_{1}e^{-t},\,y_{2}(t)=c_{2}e^{2t}$ ή, σε μορφή πινάκων

\bm{y}(t)=\left[\begin{array}[]{cc}e^{-t}&0\\ 0&e^{2t}\end{array}\right]\;\bm{y}(0),

όπου θέσαμε $\bm{y}(0)=[c_{1},c_{2}]^{T}$ . Τελικά έχουμε

\bm{x}(t)=\bm{P}\left[\begin{array}[]{cc}e^{-t}&0\\ 0&e^{2t}\end{array}\right]\bm{P}^{-1}\;\bm{x}(0)\Rightarrow\begin{cases}x_{1}(% t)=x_{1}(0)e^{-t}+x_{2}(0)(e^{-t}-e^{2t})\\ x_{2}(t)=x_{2}(0)e^{2t}\end{cases}

Σύντομο πρόβλημα 3.1.

Για το σύστημα του προηγουμένου παραδείγματος σχεδιάστε τα διαγράμματα φάσεων στα επίπεδα $(y_{1},y_{2})$ και $(x_{1},x_{2})$ .

3.1.4 Μιγαδικές ιδιοτιμές

Ας δούμε τώρα την περίπτωση που οι λύσεις της χαρακτηριστικής εξίσωσης είναι μιγαδικές, δηλαδή, ο πίνακας του συστήματος έχει μιγαδικές ιδιοτιμές.

Παράδειγμα 3.6.

(Εστία) Έστω το γραμμικό σύστημα

	$\displaystyle\dot{x}_{1}$	$\displaystyle=ax_{1}-bx_{2}$
	$\displaystyle\dot{x}_{2}$	$\displaystyle=bx_{1}+ax_{2}$		(3.37)

του οποίου η χαρακτηριστική εξίσωση είναι

\left|\begin{array}[]{cc}a-\lambda&-b\\ b&a-\lambda\end{array}\right|=0\Rightarrow(\lambda^{2}-a)^{2}+b^{2}=0,% \Rightarrow\lambda=a\pm ib.

Τα αντίστοιχα ιδιοδιανύσματα είναι $(1,\mp i)$ . Άρα

	$\displaystyle x_{1}(t)$	$\displaystyle=r_{1}e^{(a+ib)t}+r_{2}e^{(a-ib)t}=e^{at}[r_{1}e^{ibt}+r_{2}e^{-% ibt}]$
	$\displaystyle x_{2}(t)$	$\displaystyle=-ir_{1}e^{(a+ib)t}+ir_{2}e^{(a-ib)t}=e^{at}\frac{1}{i}[r_{1}e^{% ibt}-r_{2}e^{-ibt}]$

Θέτουμε $r_{2}^{*}$ τον μιγαδικός συζυγή του $r_{2}$ . Εκλέγουμε $r_{2}^{*}=r_{1}$ και $r_{1}:=c_{1}/2+ic_{2}/2$ όπου $c_{1},c_{2}\in\mathbb{R}$ , ώστε να πετύχουμε πραγματική λύση (αφού σε όλα το παρόν κεφάλαιο υποθέτουμε ότι τα $x, y$ είναι πραγματικές μεταβλητές). Αντικαθιστούμε στη γενική λύση και βρίσκουμε

	$\displaystyle x_{1}(t)$	$\displaystyle=e^{at}\,2{\rm Re}[r_{1}e^{ibt}]=e^{at}\,[c_{1}\cos bt-c_{2}\sin bt]$
	$\displaystyle x_{2}(t)$	$\displaystyle=e^{at}\,2{\rm Im}[r_{1}e^{ibt}]=e^{at}\,[c_{1}\sin bt+c_{2}\cos bt].$

Η λύση αυτή γράφεται και στη μορφή

\bm{x}(t)=e^{at}\left[\begin{array}[]{cc}\cos bt&-\sin bt\\ \sin bt&\cos bt\end{array}\right]\bm{x}(0),

(3.38)

όπου $\bm{x}=[x_{1},x_{2}]^{T}$ και $\bm{x}(0)=\bm{x}(t=0)$ είναι οι αρχικές συνθήκες.

Παρατηρούμε ότι στην Εξ. (3.38) ο πίνακας στο δεξιό μέλος δίνει στροφή το $\bm{x}_{0}$ κατά γωνία $b t$ ενώ το εκθετικό δίνει είτε αύξηση (αν $a>0$ ) είτε συρρίκνωση (αν $a<0$ ) του μέτρου του $\bm{x}(t)$ .

Εστία σε πολικές συνεταγμένες

Η τελευταία παρατήρηση υποδεικνύει ότι μία απλούστερη και παραστατικότερα μελέτη του συστήματος (3.6) και των λύσεών του μπορεί να επιτευχθεί αν χρησιμοποιήσουμε πολικές συντεταγμένες [17]. Ξεκινάμε ορίζοντας τη μιγαδική μεταβλητή $z=x_{1}+ix_{2}$ . Άμεσος υπολογισμός δείχνει ότι το σύστημα (3.6), γράφεται στη συμπαγή μορφή

\dot{z}=(a+ib)\,z.

(3.39)

Στη συνέχεια εισάγουμε τις πολικές συντεταγμένες $(r,\theta)$ και χρησιμοποιούμε την πολική μορφή για τη μιγαδική μεταβλητή $z=r(t)e^{i\theta(t)}$ , οπότε η Εξ. (3.39) γράφεται ως

\begin{cases}\dot{r}&=ar\\ \dot{\theta}&=b\end{cases}\Rightarrow\begin{cases}r=r_{0}\,e^{at}\\ \theta=bt+\theta_{0},\end{cases}

(3.40)

όπου $r_{0},\theta_{0}$ είναι σταθερές. Αυτή η μορφή της λύσης δείχνει ότι η χρονική εξέλιξη κάθε σημείου στο διάγραμμα φάσεων δίνει περιστροφή γύρω από την αρχή των αξόνων, ενώ ταυτοχρόνως πλησιάζει (για $a<0$ ) ή απομακρύνεται (για $a>0$ ) από αυτό. Λέμε ότι η αρχή των αξόνων είναι ένα σπειροειδές σημείο ισορροπίας (εστία). Αυτό είναι ευσταθές για $a<0$ και ασταθές για $a>0$ .

Παρατήρηση 3.11.

(Εστία) Ένα σημείο ισορροπίας με δύο μιγαδικές συζυγείς ιδιοτιμές λέγεται εστία ή σπειροειδές σημείο. Όταν το πραγματικό μέρος των ιδιοτιμών είναι αρνητικό τότε η κίνηση είναι προς τα μέσα (έχουμε μία ευσταθή εστία). Στην αντίθετη περίπτωση (πραγματικό μέρος των ιδιοτιμών θετικό) η κίνηση είναι προς τα έξω (έχουμε μία ασταθή εστία).

Παρατήρηση 3.12.

(Κέντρο) Στην περίπτωση $a=0$ έχουμε κλειστές τροχιές, οι οποίες είναι κύκλοι ή ελλείψεις και λέμε ότι το σημείο ισορροπίας είναι κέντρο.

Οποιοδήποτε σύστημα της μορφής

	$\displaystyle\dot{x}_{1}$	$\displaystyle=ax_{1}+bx_{2}$
	$\displaystyle\dot{x}_{2}$	$\displaystyle=cx_{1}+dx_{2}$

για τον οποίο έχουμε μιγαδικές ιδιοτιμές έχει ένα σπειροειδές σημείο ισορροπίας. Αυτό προκύπτει από το ακόλουθο θεώρημα [15, 29].

Θεώρημα.

Εάν ένας πραγματικός πίνακας $\bm{A}$ διαστάσεων $2n\times 2n$ έχει διάκριτες ιδιοτιμές $\lambda_{j}=a_{j}+ib_{j}$ και $\lambda_{j}^{*}=a_{j}-ib_{j}$ και ιδιοδιανύσματα $\bm{w}_{j}=\bm{u}_{j}+i\bm{v}_{j},\;\bm{w}_{j}^{*}=\bm{u}_{j}-i\bm{v}_{j}$ , τότε $\{\bm{u}_{1},\bm{v}_{1},\ldots,\bm{u}_{n},\bm{v}_{n}\}$ είναι βάση του $\mathbb{R}^{2n}$ . Ο πίνακας $\bm{P}=[\bm{v}_{1},\bm{u}_{1},\ldots,\bm{v}_{n},\bm{u}_{n}]$ είναι αντιστρέψιμος και

\bm{P}^{-1}\bm{A}\bm{P}={\rm diag}\left[\begin{array}[]{cc}a_{j}&-b_{j}\\ b_{j}&a_{j}\end{array}\right].

(3.41)

Ώστε, εάν ορίσουμε ένα νέο διάνυσμα μεταβλητών $\bm{y}=\bm{P}^{-1}\bm{x}$ , έχουμε

\dot{\bm{y}}=\bm{P}^{-1}\dot{\bm{x}}=\bm{P}^{-1}\bm{A}\bm{x}=\bm{P}^{-1}\bm{A}% \bm{P}\bm{y}={\rm diag}\left[\begin{array}[]{cc}a_{j}&-b_{j}\\ b_{j}&a_{j}\end{array}\right]\bm{y}.

(3.42)

Άρα ισχύει

\bm{x}(t)=\bm{P}\,{\rm diag}\left[\begin{array}[]{cc}a_{j}&-b_{j}\\ b_{j}&a_{j}\end{array}\right]\bm{P}^{-1}\bm{x}(0).

(3.43)

Παράδειγμα 3.7.

(Εστία) Έστω το γραμμικό σύστημα

	$\displaystyle\dot{x}_{1}$	$\displaystyle=x_{1}+x_{2}$
	$\displaystyle\dot{x}_{2}$	$\displaystyle=-5x_{1}-3x_{2}.$

Βρείτε τη γενική λύση του.

Επίλυση.

Η χαρακτηριστική εξίσωση του συστήματος είναι

\lambda^{2}-2\lambda+2=0\Rightarrow\lambda_{1},\;\lambda_{2}=-1\pm i

Τα αντίστοιχα ιδιοδιανύσματα είναι $(x_{1},x_{2})=(1,-2\pm i)$ . Άρα

\bm{P}=\left[\begin{array}[]{cc}0&1\\ 1&-2\end{array}\right],\qquad\bm{P}^{-1}=\left[\begin{array}[]{cc}2&1\\ 1&0\end{array}\right].

Αν κάνουμε τον μετασχηματισμό $\bm{y}=\bm{P}^{-1}\bm{x}$ τότε βρίσκουμε $\dot{\bm{y}}=\bm{P}^{-1}\dot{\bm{x}}=\bm{P}^{-1}\bm{A}\bm{x}=\bm{P}^{-1}\bm{A}% \bm{P}\bm{y}$ . Σε συμφωνία με το παραπάνω θεώρημα έχουμε

\dot{\bm{y}}=\left[\begin{array}[]{cc}-1&-1\\ 1&-1\end{array}\right]\bm{y}.

Από το Παράδειγμα 3.6 (όπου θέτουμε $a=-1,b=1$ ) συνάγουμε

\bm{y}(t)=e^{-t}\left[\begin{array}[]{cc}\cos t&-\sin t\\ \sin t&\cos t\end{array}\right]\bm{y}(0).

Τελικά

	$\displaystyle\bm{x}(t)=\bm{P}\bm{y}(t)$	$\displaystyle=\bm{P}e^{-t}\left[\begin{array}[]{cc}\cos t&-\sin t\\ \sin t&\cos t\end{array}\right]\bm{y}(0)=\bm{P}e^{-t}\left[\begin{array}[]{cc}% \cos t&-\sin t\\ \sin t&\cos t\end{array}\right]\bm{P}^{-1}\bm{x}(0)$
	$\displaystyle\Rightarrow$	$\displaystyle\begin{cases}x_{1}(t)&=e^{-t}\,[x_{1}(0)\cos t+(2x_{1}(0)+x_{2}(0% ))\sin t]\\ x_{2}(t)&=e^{-t}\,[x_{2}(0)\cos t-(5x_{1}(0)+2x_{2}(0))\sin t]\end{cases}$

Στo διάγραμμα φάσεων στo επίπεδo $(x_{1},x_{2})$ έχουμε μία ευσταθή εστία.

Παράδειγμα 3.8.

(Εστία) Βρείτε τη γενική λύση του συστήματος

	$\displaystyle\dot{x}_{1}$	$\displaystyle=x_{1}+x_{2}$
	$\displaystyle\dot{x}_{2}$	$\displaystyle=-5x_{1}-3x_{2}.$

Επίλυση.

Η χαρακτηριστική εξίσωση μας δίνει

\lambda^{2}+2\lambda+2=0\Rightarrow\lambda_{1}=-1+i,\quad\lambda_{2}=-1-i,

όπου $\lambda_{2}=\lambda_{1}^{*}$ . Για $\lambda=\lambda_{1}$ και $\lambda=\lambda_{2}$ βρίσκουμε αντιστοίχως

s_{1}=(-2+i)r_{1},\qquad s_{2}=(-2-i)r_{2}.

Άρα η γενική λύση γράφεται

	$\displaystyle x_{1}(t)$	$\displaystyle=r_{1}\,e^{(-1+i)t}+r_{2}\,e^{(-1-i)t},$
	$\displaystyle x_{2}(t)$	$\displaystyle=r_{1}(-2+i)\,e^{(-1+i)t}+r_{2}(-2-i)\,e^{(-1-i)t}.$

Αν ζητάμε πραγματικές λύσεις τότε πρέπει να θέσουμε $r_{2}=r_{1}^{*}$ και γράφοντας $r_{1}=\frac{1}{2}c_{1}+\frac{1}{2}ic_{2}$ παίρνουμε

	$\displaystyle x_{1}(t)$	$\displaystyle=e^{-t}(c_{1}\cos t-c_{2}\sin t),$
	$\displaystyle x_{2}(t)$	$\displaystyle=-e^{-t}[(2c_{1}+c_{2})\cos t+(c_{1}-2c_{2})\sin t].$

Για να σχεδιάσουμε το διάγραμμα φάσεων δουλεύουμε ως εξής. Σχεδιάζουμε μία σπείρα στην οποία τα βέλη οδηγούν προς το σημείο ισορροπίας, διότι το πραγματικό μέρος των ιδιοτιμών είναι αρνητικό. Υπάρχουν δύο τέτοιες σπείρες (αριστερόστροφη και δεξιόστροφη). Επιλέγουμε εκείνη που ικανοποιεί τις εξισώσεις, πράγμα που το ελέγχουμε με υπολογισμό των $\dot{x}_{1},\dot{x}_{2}$ σε ορισμένα σημεία του διαγράμματος φάσεων.

3.1.5 Κατάταξη σημείων ισορροπίας

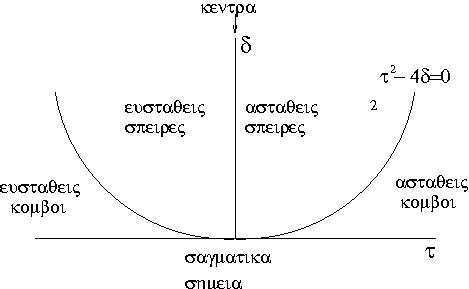
Έστω η γενική μορφή για το σύστημα δύο γραμμικών διαφορικών εξισώσεων

\begin{split}\displaystyle\dot{x}_{1}&\displaystyle=ax_{1}+bx_{2}\\ \displaystyle\dot{x}_{2}&\displaystyle=cx_{1}+dx_{2}.\end{split}

(3.44)

Θέτουμε $\delta={\rm det}\bm{A}=ad-bc$ και $\tau={\rm Tr}\,\bm{A}=a+d$ . Η χαρακτηριστική εξίσωση γράφεται ως

\lambda^{2}-\tau\lambda+\delta=0\Rightarrow\lambda_{1,2}=\frac{\tau\pm\sqrt{% \tau^{2}-4\delta}}{2}

(3.45)

Έχουμε τις παρακάτω περιπτώσεις, τις οποίες μελετήσαμε στις προηγούμενες παραγράφους.

(α)

Για $\delta<0$ έχουμε σαγματικό σημείο.
(β)

Για $\delta>0$ και $\tau^{2}-4\delta\geq 0$ έχουμε κόμβο. Είναι ευσταθής για $\tau<0$ και ασταθής για $\tau>0$ .
(γ)

Για $\delta>0$ και $\tau^{2}-4\delta<0$ έχουμε εστία (για $\tau\neq 0$ ). Είναι ευσταθής για $\tau<0$ και ασταθής για $\tau>0$ .
(δ)

Για $\delta>0$ και $\tau=0$ έχουμε κέντρο.

Σχήμα 3.3: Διάγραμμα σημείων ισορροπίας στο χώρο των παραμέτρων.

3.1.6 Ευστάθεια σημείων ισορροπίας

Είδαμε την περίπτωση του κέντρου ως σημείου ισορροπίας το οποίο περιβάλλεται από κλειστές καμπύλες. Αυτό σημαίνει ότι όταν το σύστημα βρεθεί κοντά σε αυτό το σημείο ισορροπίας θα εξελίσσεται στον χρόνο ώστε να παραμένει συνεχώς στην περιοχή του κέντρου. Στην περίπτωση του σάγματος, οι τροχιές στο διάγραμμα φάσης οι οποίες περνούν κοντά από το σάγμα εξελίσσονται στον χρόνο έτσι ώστε η κατάσταση του συστήματος να απομακρύνεται από το σάγμα. Γενικότερα, αν μία μικρή διαταραχή από το σημείο ισορροπίας δεν οδηγεί (μέσω κάποιων φασικών καμπυλών) μακριά από αυτό, τότε ονομάζουμε το σημείο ισορροπίας ευσταθές. Εάν, αντίθετα, μία μικρή διαταραχή από το σημείο ισορροπίας οδηγεί (μέσω κάποιων φασικών καμπυλών) μακριά από αυτό, τότε ονομάζουμε το σημείο ισορροπίας ασταθές. Θα δούμε στην παράγραφο αυτή μερικά αποτελέσματα σχετικά με την ευστάθεια σημείων ισορροπίας [15, 29, 35].

Θεώρημα.

Εάν όλες οι ιδιοτιμές του πίνακα $\bm{A}$ ενός γραμμικού συστήματος $n$ εξισώσεων έχουν αρνητικό πραγματικό μέρος τότε: για κάθε αρχική συνθήκη $\bm{x}_{0}\in\mathbb{R}^{n}$ ισχύει $\lim_{t\to\infty}{\bm{x}}(t)=\bm{0}$ και επίσης, αν $\bm{x}_{0}\neq\bm{0}$ , $\lim_{t\to-\infty}|\bm{x}(t)|=\infty$ .

Θεώρημα.

Εάν όλες οι ιδιοτιμές του πίνακα $\bm{A}$ έχουν θετικό πραγματικό μέρος τότε: για κάθε αρχική συνθήκη $\bm{x}_{0}\in\mathbb{R}^{n}$ ισχύει $\lim_{t\to-\infty}{\bm{x}}(t)=\bm{0}$ και επίσης, αν $\bm{x}_{0}\neq\bm{0}$ , $\lim_{t\to\infty}|\bm{x}(t)|=\infty$ .

Ορισμός.

Έστω $\lambda_{j}=a_{j}+ib_{j}$ οι ιδιοτιμές του πίνακα ενός γραμμικού συστήματος και $\bm{w}_{j}=\bm{u}_{j}+i\bm{v}_{j}$ τα αντίστοιχα ιδιοδιανύσματα. Τότε ονομάζουμε τους χώρους

	$\displaystyle E^{s}$	$\displaystyle={\rm Span}\{\bm{u}_{j},\bm{v}_{j}\,\|\,a_{j}<0\}$
	$\displaystyle E^{u}$	$\displaystyle={\rm Span}\{\bm{u}_{j},\bm{v}_{j}\,\|\,a_{j}>0\}$
	$\displaystyle E^{c}$	$\displaystyle={\rm Span}\{\bm{u}_{j},\bm{v}_{j}\,\|\,a_{j}=0\}$

ευσταθή, ασταθή και κεντρικό υπόχωρο του συστήματος αντίστοιχα.

Παρατήρηση 3.13.

Για ένα σύστημα δύο εξισώσεων με ένα σαγματικό σημείο ο ευσταθής και ο ασταθής υπόχωρος είναι ο καθένας μία ευθεία.

Παράδειγμα 3.9.

Έστω ο πίνακας

\bm{A}=\left[\begin{array}[]{ccc}-2&-1&0\\ -1&-2&0\\ 0&0&3\end{array}\right]

με ιδιοτιμές $\lambda_{1,2}=-2\pm i$ και ιδιοδιανύσματα $\bm{w}_{1,2}=[0,1,0]^{T}\pm i[1,0,0]^{T}$ και επίσης $\lambda_{3}=3$ με ιδιοδιάνυσμα $\bm{u}_{3}=[0,0,1]^{T}$ . Ο ευσταθής υπόχωρος $E^{s}$ είναι το επίπεδο $(x_{1},x_{2})$ και ο ασταθής υπόχωρος $E^{u}$ είναι ο άξονας $x_{3}$ .

Θεώρημα.

Οι υπόχωροι $E^{s},E^{u},E^{c}$ ενός πίνακα $n\times n$ μένουν αναλλοίωτοι από τις αντίστοιχες εξισώσεις. Επίσης,

\mathbb{R}^{n}=E^{s}\oplus E^{u}\oplus E^{c}.

Ορισμός.

Ένα σημείο ισορροπίας $\bm{x}_{0}$ λέγεται ευσταθές αν για κάθε $\epsilon>0$ υπάρχει $\delta>0$ τέτοιο ώστε για κάθε αρχική συνθήκη $\bm{x}(t=0)\in N_{\delta}(\bm{x}_{0})$ έχουμε $\bm{x}(t)\in N_{\epsilon}(\bm{x}_{0})$ για κάθε χρόνο $t>0$ . Το σημείo ισορροπίας λέγεται ασταθές εάν δεν είναι ευσταθές.

Για τα σημεία ισορροπίας τα οποία έχουμε δει έχουμε τις ακόλουθες ιδιότητες ευστάθειας.

•

Ένα σαγματικό σημείο είναι ασταθές.
•

Ένας κόμβος μπορεί να είναι ασταθής (για θετικές ιδιοτιμές) ή ευσταθής (για αρνητικές ιδιοτιμές).
•

Μία εστία μπορεί να είναι ασταθής (ιδιοτιμές με θετικό πραγματικό μέρος) ή ευσταθής (ιδιοτιμές με αρνητικό πραγματικό μέρος).
•

Ένα κέντρο είναι ευσταθές.

Παρατήρηση 3.14.

Ένα σημείο ισορροπίας λέγεται ασυμπτωτικά ευσταθές αν υπάρχει $\delta>0$ τέτοιο ώστε για κάθε $\bm{x}\in N_{\delta}(\bm{x}_{0})$ έχουμε

\lim_{t\to\infty}\bm{x}(t)=0.

Παρατήρηση 3.15.

Εάν μία εστία είναι ευσταθής τότε είναι ασυμπτωτικά ευσταθής. Ένα κέντρο είναι ευσταθές, αλλά όχι ασυμπτωτικά ευσταθές.