3 Δυναμικά συστήματα 3.2 Διαφορικές εξισώσεις δεύτερης τάξης 3.4 Μελέτη

3.3 Μη γραμμικά συστήματα

’Εστω το μη γραμμικό σύστημα $n$ εξισώσεων

\dot{\bm{x}}=\bm{f}(\bm{x}),

(3.55)

όπου $\bm{x}$ είναι το διάνυσμα των $n$ μεταβλητών και $\bm{f}$ είναι διάνυσμα $n$ συναρτήσεων. Για παράδειγμα, για ένα σύστημα δύο εξισώσεων έχουμε τη μορφή

	$\displaystyle\dot{x}_{1}$	$\displaystyle=f_{1}(x_{1},x_{2})$
	$\displaystyle\dot{x}_{2}$	$\displaystyle=f_{2}(x_{1},x_{2}).$

Θεωρούμε ένα σημείο ισορροπίας του συστήματος $\bm{x}_{0}$ και τον ιακωβιανό πίνακα υπολογισμένο στο σημείο ισορροπίας (υποθέτουμε σύστημα δύο εξισώσεων)

D\bm{f}(\bm{x}_{0})=\left[\begin{array}[]{cc}df_{1}/dx_{1}&df_{1}/dx_{2}\\ df_{2}/dx_{1}&df_{2}/dx_{2}\end{array}\right]_{\bm{x}_{0}}.

Θα δούμε ότι το γραμμικό σύστημα

\dot{\bm{\xi}}=D\bm{f}(\bm{x}_{0})\,\bm{\xi},\qquad\bm{\xi}:=\bm{x}-\bm{x}_{0}

(3.56)

διατηρεί (στη γενική περίπτωση), κοντά στο σημείο ισορροπίας $\bm{x}_{0}$ τη μορφή του διαγράμματος φάσεων του μη γραμμικού συστήματος [15, 17, 29, 35].

Θεώρημα.

(Το θεώρημα ευσταθούς πολλαπλότητας) Έστω $E$ ένα ανοιχτό υποσύνολο του $\mathbb{R}^{n}$ που περιέχει την αρχή των αξόνων, επίσης $\bm{f}\in C^{1}(E)$ , όπου $\dot{\bm{x}}=\bm{f}(\bm{x})$ . Υποθέτουμε ότι $\bm{f}(\bm{0})=\bm{0}$ και ότι $D\bm{f}(\bm{0})$ έχει $k$ ιδιοτιμές με αρνητικό πραγματικό μέρος και $n-k$ ιδιοτιμές με θετικό πραγματικό μέρος. Τότε υπάρχει μία διαφορίσιμη πολλαπλότητα $S$ διαστάσεως $k$ η οποία είναι εφαπτόμενη στον ευσταθή υπόχωρο $E^{s}$ του γραμμικοποιημένου συστήματος (3.56) στο σημείο $\bm{0}$ τέτοια ώστε για κάθε αρχική συνθήκη $\bm{x}_{0}\in S$

\lim_{t\to\infty}\bm{x}(t)=\bm{0}.

Επίσης, υπάρχει μία πολλαπλότητα $U$ διαστάσεως $n-k$ εφαπτόμενη στον ασταθή υπόχωρο $E^{u}$ του γραμμικοποιημένου συστήματος στο σημείο $\bm{0}$ τέτοια ώστε για κάθε αρχική συνθήκη $\bm{x}_{0}\in U$

\lim_{t\to-\infty}\bm{x}(t)=\bm{0}.

Οι πολλαπλότητες $S$ και $U$ είναι αναλλοίωτες στις εξισώσεις κίνησης.

Με βάση το παραπάνω θέωρημα μπορούμε να διατυπώσουμε την πρόταση ότι, αν ένα σημείο ισορροπίας έχει όλες τις ιδιοτιμές με μη-μηδενικό πραγματικό μέρος (οπότε λέγεται υπερβολικό σημείο ισορροπίας), τότε η συμπεριφορά του μη γραμμικού συστήματος στην περιοχή του σημείου ισορροπίας είναι τοπολογικά ισοδύναμη με τη συμπεριφορά του γραμμικοποιημένου συστήματος.

Παράδειγμα 3.13.

Βρείτε τα σημεία ισορροπίας και σχεδιάστε το διάγραμμα φάσεων του μη γραμμικού συστήματος

\dot{x}_{1}=x_{1}(1-x_{2})+2,\qquad\dot{x}_{2}=x_{1}-x_{2}.

Επίλυση.

Σχήμα 3.6: Διάγραμμα φάσεων για το μη γραμμικό πρόβλημα του παραδείγματος. Έχουμε μία ευσταθή εστία και ένα σαγματικό σημείο.

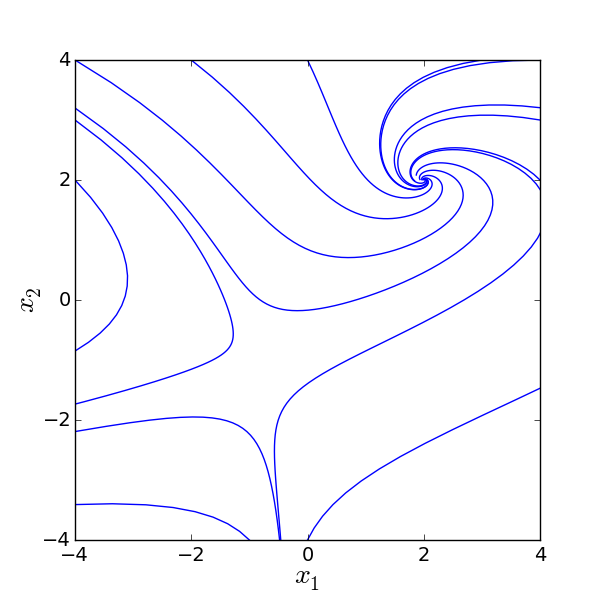
Θέτουμε $f_{1}=x_{1}(1-x_{2})+2,\;f_{2}=x_{1}-x_{2}$ . Τα σημεία ισορροπίας βρίσκονται ως

		$\displaystyle f_{2}=0\Rightarrow x_{1}-x_{2}=0\Rightarrow x_{1}=x_{2}$
		$\displaystyle f_{1}=0\Rightarrow x_{1}(1-x_{2})+2=0\Rightarrow x_{1}^{2}-x_{1}% -2=0\Rightarrow x_{1}=-1,2.$

Άρα έχουμε τα σημεία $(-1,-1)$ και $(2,2)$ .

Ο πίνακας του γραμμικοποιημένου συστήματος είναι

\left[\begin{array}[]{cc}df_{1}/dx_{1}&df_{1}/dx_{2}\\ df_{2}/dx_{1}&df_{2}/dx_{2}\end{array}\right]=\left[\begin{array}[]{cc}1-x_{2}% &-x_{1}\\ 1&-1\end{array}\right].

Για το σημείο $(-1,-1)$ ορίζουμε $\xi_{1}=x_{1}+1,\,\xi_{2}=x_{2}+1$ και έχουμε το γραμμικοποιημένο σύστημα

\left[\begin{array}[]{c}\dot{\xi}_{1}\\ \dot{\xi}_{2}\end{array}\right]=\left[\begin{array}[]{cc}2&1\\ 1&-1\end{array}\right]\;\left[\begin{array}[]{c}\xi_{1}\\ \xi_{2}\end{array}\right].

Οι ιδιοτιμές του είναι $\lambda_{1,2}=(1\pm\sqrt{13})/2$ , άρα το σημείο είναι σαγματικό. Τα αντίστοιχα ιδιοδιανύσματα είναι $(1,(\sqrt{13}-3)/2)$ και ορίζουν αντίστοιχα τον ασταθή και ευσταθή υπόχωρο του γραμμικοποιημένου συστήματος.

Για το σημείο $(2,2)$ ορίζουμε $\xi_{1}=x_{1}-2,\,\xi_{2}=x_{2}-2$ και έχουμε το γραμμικοποιημένο σύστημα

\left[\begin{array}[]{c}\dot{\xi}_{1}\\ \dot{\xi}_{2}\end{array}\right]=\left[\begin{array}[]{cc}-1&-2\\ 1&-1\end{array}\right]\;\left[\begin{array}[]{c}\xi_{1}\\ \xi_{2}\end{array}\right].

Οι ιδιοτιμές του είναι $\lambda_{1,2}=-1\pm i\sqrt{2}$ , άρα το σημείο ισορροπίας είναι μία ευσταθής εστία. Η φορά περιστροφής των σπειρών μπορεί να βρεθεί ως εξής. Στις γραμμικοποιημένες εξισώσεις θεωρούμε, π.χ., $\xi_{2}=0,\xi_{1}>0$ (δηλ., είμαστε στον θετικό άξονα $\xi_{1}$ ) και βρίσκουμε $\dot{\xi}_{1}<0,\;\dot{\xi}_{2}>0$ , άρα η κίνηση επάνω στη σπείρα είναι αντίθετη της φοράς των δεικτών του ρολογίου.