1.2 Διαστατική Ανάλυση

Έστω η παρακάτω, αρκετά γενική, χημική αντίδραση, στην οποία $\mathrm{{\rm A}}$ αντιδρώντα, μετατρέπονται σε προϊόντα:

$$A⟶\text{προϊόντα}$$

Θεωρούμε ότι η αντίδραση συμβαίνει σε έναν χημικό αντιδραστήρα, όπως στο σχήμα 1.2.

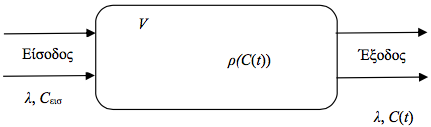
Στη γενική περίπτωση τα αντιδρώντα είναι $N$ διαφορετικές ουσίες (χημικές ενώσεις). Θα παραστήσουμε με $C_i,i=1,2,\mathrm{\dots },N$ οι συγκεντρώσεις των ουσιών δηλαδή η μάζα κάθε ουσίας ανά μονάδα όγκου. Για να διευκολύνουμε τη μελέτη του προβλήματος θεωρούμε απλοποιήσεις για τη χημική αντίδραση και κάνουμε τις παρακάτω υποθέσεις:

• •

  Θεωρούμε «απλή» χημική αντίδραση, τα αντιδρώντα είναι μόνο μία ουσία ($N=1$), την οποία θα ονομάσουμε $A$.

• •

  Θεωρούμε ισόθερμο αντιδραστήρα συνεχούς ανάδευσης. Σε αυτή την περίπτωση η θερμοκρασία μέσα στον αντιδραστήρα είναι σταθερή, $T=T_0$ και η συγκέντρωση του αντιδρώντος $C$ είναι συνάρτηση μόνο του χρόνου και όχι του χώρου, δηλαδή $C=C(t)$.

• •

  Θεωρούμε σταθερή παροχή $\lambda$ για τo αντιδρών στην είσοδο του αντιδραστήρα, όπου $\lambda$ είναι ο όγκος ουσίας $A$ ο οποίος παρέχεται ανά μονάδα χρόνου.

Επίσης, θα απλοποιήσουμε σε έναν βαθμό τις παραμέτρους του προβλήματος:

• •

  Θεωρούμε ότι η παροχή στην έξοδο είναι ίση με την παροχή στην είσοδο $\lambda$, δηλαδή ο όγκος της ουσίας που αποβάλλεται είναι συνεχώς ίσος με τον όγκο της ουσίας που εισάγεται.

• •

  Θεωρούμε ότι ο όγκος του αντιδραστήρα $V$ είναι μοναδιαίος $(V=1)$.

Παρότι θεωρήσαμε την παροχή στην έξοδο ίση με την παροχή στην είσοδο, η συγκέντρωση όμως της ουσίας $C$ στην έξοδο θα είναι διαφορετική από αυτή στην είσοδο και αυτή μπορεί να μεταβάλλεται με τον χρόνο $t$. Το πρόβλημα λοιπόν που έχουμε να μελετήσουμε είναι το πώς μεταβάλλεται στο χρόνο η συγκέντρωση $C=C(t)$ του αντιδρώντος στην έξοδο του αντιδραστήρα. Για να πετύχουμε την περιγραφή της συγκέντρωσης εξόδου χρειαζόμαστε ένα μαθηματικό μοντέλο, το οποίο θα περιγράφει πως μεταβάλλεται στο χρόνο η συγκέντρωση $C=C(t)$. Αν θεωρήσουμε τη $C$ ως συνεχή μεταβλητή, η παράγωγος της οποίας υπάρχει, χρειαζόμαστε την μεταβολή της με τον χρόνο. Χρειαζόμαστε δηλαδή μια σχέση της μορφής:

$$\frac{d}{dt}C(t)=F(t,C)$$

(1.1)

όπου $F(t,C)$ είναι μια συνάρτηση η οποία εξαρτάται από τον χρόνο και τη συγκέντρωση $C$. Το δεύτερο στάδιο λοιπόν της διαδικασίας αφορά την εύρεση της, καταρχήν άγνωστης, συνάρτησης $F(t,C)$.

Για την πλήρη περιγραφή της αντίδρασης χρειάζεται να γνωρίζουμε τις διεργασίες που συμβαίνουν στο εσωτερικό του αντιδραστήρα. Ας ορίσουμε ως:

• •

  $V\rho (C)=\rho (C)$ τον ρυθμό αντίδρασης (reaction rate), ή ρυθμό κατανάλωσης της ουσίας $A$ εντός του αντιδραστήρα. Η $\rho$ δίνει τη συγκέντρωση ουσίας ανά μονάδα χρόνου η οποία καταναλώνεται και η $V\rho =\rho$ είναι η μάζα ουσίας ανά μονάδα χρόνου (έχει μονάδες kg/sec). Η εξάρτησή της $\rho$ από την $C$ μπορεί να έχει διάφορες μορφές οι οποίες θα δώσουν διαφορετικά προβλήματα.

Για να βρούμε τη μορφή της συνάρτησης $F(t,C)$ θα θεωρήσουμε το ισοζύγιο μάζας για το αντιδρών κατά τη διαδικασία της αντίδρασης. Δεδομένων των παραπάνω ορισμών, έχουμε:

• •

  $\lambda C_{\epsilon \iota \sigma }$: μάζα ουσίας ανά μονάδα χρόνου στην είσοδο του αντιδραστήρα.

• •

  $\lambda C(t)$: μάζα ουσίας ανά μονάδα χρόνου στην έξοδο του αντιδραστήρα.

• •

  $V\rho (C(t))=\rho (C(t))$: μάζα ουσίας ανά μονάδα χρόνου που καταναλώνεται μέσα στον αντιδραστήρα (θυμηθείτε ότι ο όγκος $V$ θεωρήθηκε μοναδιαίος).

• •

  $VC(t)=C(t)$: μάζα ουσίας μέσα στον αντιδραστήρα, σε χρόνο $t$.

Στον αντιδραστήρα εισέρχεται λοιπόν μάζα $\lambda C_{\epsilon \iota \sigma }$, ενώ απορρίπτεται (εξέρχεται) και καταναλώνεται μάζα $\lambda C(t)+\rho (C(t))$. Θα θεωρήσουμε ότι δεν έχουμε μεταβολή της μάζας εντός του αντιδραστήρα ώστε το ισοζύγιο μάζας εκφράζεται από τη συνθήκη:

$$\text{μάζα στην είσοδο}=\text{μάζα στην έξοδο},$$

η οποία επιβάλλεται αν ικανοποιείται η εξίσωση

$$\lambda C_{\epsilon \iota \sigma }=\lambda C(t)+\rho (C(t)).$$

Γενικεύοντας την παραπάνω σκέψη μπορούμε να γράψουμε μία εξίσωση της μορφής (1.1) για το ισοζύγιο μάζας στη γενική περίπτωση που η μάζα των αντιδρώντων μέσα στον αντιδραστήρα μεταβάλλεται με τον χρόνο. Εφόσον η μάζα του αντιδρώντος εντός του αντιδραστήρα είναι $VC=C$, είναι:

$$\frac{d}{dt}C(t)=\lambda C_{\epsilon \iota \sigma }-\lambda C(t)-\rho (C(t)).$$

(1.2)

Η παραπάνω εξίσωση εκφράζει ότι η διαφορά του ρυθμού εισόδου μάζας με τον ρυθμό εξόδου μάζας ισούται με τη μεταβολή της μάζας του αντιδρώντος εντός του αντιδραστήρα.

Για να προχωρήσουμε στην επίλυση της Εξ. (1.2) χρειαζόμαστε μια σχέση για την εξάρτηση του ρυθμού αντίδρασης $\rho$ από τη συγκέντρωση $C$. Υποθέτοντας μία απλή γραμμική εξάρτηση (χημική αντίδραση 1ης τάξης) γράφουμε:

$$\rho (C)=kC$$

όπου $k$ είναι μια σταθερά με μονάδες αντιστρόφου χρόνου. Η σχέση αυτή υποθέτει ότι ο ρυθμός αντίδρασης αυξάνεται γραμμικά με τη συγκέντρωση του αντιδρώντος, πράγμα που μπορεί να θεωρηθεί μία λογική προσέγγιση της χημικής διαδικασίας. Σε αυτήν την περίπτωση η Εξ. (1.2) γίνεται:

$$\frac{d}{dt}C(t)=\lambda C_{\epsilon \iota \sigma }-\lambda C(t)-kC(t).$$

(1.3)

Με μια γενική αρχική συνθήκη για την αρχική συγκέντρωση, έστω $C(t=0)=C_0$, το παραπάνω γίνεται ένα κλασικό Πρόβλημα Αρχικών Τιμών (ΠΑΤ).

Στο επόμενο στάδιο εξετάζουμε πώς το ΠΑΤ (1.3) μπορεί να απλοποιηθεί επιλέγοντας κατάλληλες νέες και αδιάστατες μεταβλητές. Αυτές θα προκύψουν από την κατάλληλη κανονικοποίηση των αρχικών μεταβλητών για τη συγκέντρωση $C$ και τον χρόνο $t$ με χαρακτηριστικές σταθερές. Στο παράδειγμά μας υπάρχουν οι ακόλουθες παράμετροι:

• •

  Ο ρυθμός $k$, ο οποίος καθορίζει τον ρυθμό με τον οποίο καταναλώνεται το αντιδρών, άρα εισάγει έναν χαρακτηριστικό χρόνο $1/k$ στον οποίο συμβαίνουν οι μεταβολές της μεταβλητής $C$.

• •

  Άλλος χαρακτηριστικός χρόνος εισάγεται από τον συνδυασμό παραμέτρων $V/\lambda =1/\lambda$.

• •

  Η συγκέντρωση εισόδου $C_{\epsilon \iota \sigma }$ είτε η αρχική συγκέντρωση $C_0$ εντός του αντιδραστήρα καθορίζουν χαρακτηριστικές συγκεντρώσεις της ουσίας στο παρόν πρόβλημα.

Οι ζητούμενες νέες μεταβλητές μπορεί να προέρχονται από κανονικοποίηση του χρόνου $t$ και της συγκέντρωσης $C$ με βάση τις χαρακτηριστικές τιμές που εξηγήθηκαν παραπάνω. Θα δούμε δύο διαφορετικές δυνατότητες.

Α) Έστω ότι επιλέγουμε ως χαρακτηριστικές τιμές για τη συγκέντρωση την $C_{\epsilon \iota \sigma }$ και για τον χρόνο τον $T=1/k$. Ορίζουμε τις νέες μεταβλητές ως:

$$\tilde{C}=\frac{C}{C_{\epsilon \iota \sigma }},\tau =\frac{t}{T}=kt.$$

(1.4)

Παρατηρήστε ότι οι νέες μεταβλητές είναι αδιάστατες, δηλαδή δεν δίνουν τιμές σε φυσικές μονάδες (sec κλπ), αλλλά μετρούν τα αντίστοιχα μεγέθη σε σχέση με τις φυσιολογικές μονάδες του παρόντος προβλήματος. Με τη χρήση των νέων μεταβλητών το αρχικό ΠΑΤ γίνεται

$$\frac{d}{d\tau }\tilde{C}(\tau )=\frac{1}{\beta }\left(1-\tilde{C}(\tau )\right)-\tilde{C}(\tau )$$

(1.5)

όπου έχουμε ορίσει την παράμετρο

$$\beta =\frac{k}{\lambda }$$

(1.6)

και παρατηρούμε ότι αυτή είναι η μόνη παράμετρος η οποία εμφανίζεται στην εξίσωση.

Β) Κάνοντας μία διαφορετική επιλογή για τον χαρακτηριστικό χρόνο, $T=1/\lambda$, μπορούμε να ορίσουμε τις νέες μεταβλητές, ως:

$$\tilde{C}=\frac{C}{C_{\epsilon \iota \sigma }},\tau =\frac{t}{T}=\lambda t.$$

(1.7)

Σε αυτή την περίπτωση το αρχικό ΠΑΤ γίνεται

$$\frac{d}{d\tau }\tilde{C}(\tau )=1-\tilde{C}(\tau )-\beta \tilde{C}(\tau )$$

(1.8)

όπου εμφανίζεται η ίδια παράμετρος $\beta$ όπως και στην (1.5).

Ένα σημαντικό πλεονέκτημα του αδιάστατου προβλήματος αρχικών τιμών και στις δύο μορφές του (Α και Β), σε σχέση με το αρχικό, είναι ότι σε αυτό έχουμε μόνο μια σταθερά, ($\beta$) ενώ στο αρχικό πρόβλημα (1.3) οι σταθερές ήταν τρεις: $k,\lambda ,C_{\epsilon \iota \sigma }$. Αυτό είναι ιδιαίτερα σημαντικό αν σκεφτούμε ότι στόχος μας είναι η πρόβλεψη της εξέλιξης της συγκέντρωσης, η επίλυση δηλαδή του ΠΑΤ, για διαφορετικές τιμές των σταθερών. Με άλλα λόγια στη δεύτερη περίπτωση θα είναι πολύ πιο εύκολο να εξετάσουμε τη συμπεριφορά του μοντέλου για διαφορετικές τιμές των (σταθερών) παραμέτρων.

Ας αναρωτηθούμε τώρα ποιά από τις δύο παραπάνω μορφές του μοντέλου είναι καλύτερο να επιλέξουμε. Δηλαδή είναι καλύτερα η αδιάστατη χρονική μεταβλητή να οριστεί μέσω του $T=k^{-1}$ ή του $T={\lambda }^{-1}$. Η επιλογή αυτή μπορεί να είναι σημαντική σε προβλήματα όπου οι δύο όροι διαφέρουν σε μεγάλο βαθμό (περισσότερο της μίας τάξης μεγέθους). Ως κανόνα θα χρησιμοποιήσουμε τον εξής:

• •

  Αν $k\gg \lambda$, τότε $\beta \gg 1$ και επιλέγουμε τη μορφή (1.5).

• •

  Αν $k\ll \lambda$, τότε $\beta \ll 1$ και επιλέγουμε τη μορφή (1.8).

Ως παράδειγμα ας εξετάσουμε τη δεύτερη περίπτωση, δηλαδή $\beta \ll 1$. Σε αυτή την περίπτωση η Εξ. (1.8) είναι προσεγγιστικά ίδια με την

$$\frac{d}{d\tau }\tilde{C}(\tau )=1-\tilde{C}(\tau )$$

(1.9)

η λύση της οποίας, με την αρχική συνθήκη $\tilde{C}(0)=C_0/C_{\epsilon \iota \sigma }=\gamma$, βρίσκεται εύκολα και είναι:

$$\tilde{C}(\tau )=1+(\gamma -1)e^{-\tau }.$$

(1.10)

Για να καταλάβουμε τι αντιπροσωπεύει αυτή η λύση όσον αφορά το πρόβλημα της χημικής αντίδρασης θα πρέπει να επαναφέρουμε τις αρχικές παραμέτρους του προβλήματος στη λύση. Χρησιμοποιώντας τους ορισμούς (1.4) η λύση (1.10) γράφεται στις αρχικές μεταβλητές του προβλήματος ως

$$\frac{C(t)}{C_{\epsilon \iota \sigma }}=1+(\gamma -1)e^{-kt}\Rightarrow C(t)=C_{\epsilon \iota \sigma }+\left(C_0-C_{\epsilon \iota \sigma }\right)e^{-kt}.$$

(1.11)

Βλέπουμε ότι η αρχική συγκέντρωση είναι $C(t=0)=C_0$ (όπως έχει επιβληθεί από την αρχική συνθήκη), ενώ $C(t\to \mathrm{\infty })=C_{\epsilon \iota \sigma }$ δηλαδή η συγκέντρωση στον αντιδραστήρα εξισώνεται τελικά με τη συγκέντρωση εισόδου. Η λύση με τέτοια συμπεριφορά μπορεί να θεωρηθεί «αναμενόμενη» καθώς η αντίδραση είναι «αργή» ($k\gg \lambda$) και η παροχή (με ρυθμό $\lambda$) αναπληρώνει άμεσα την απώλεια από την αντίδραση εντός του αντιδραστήρα. Φυσικά, η απόλυτη ισότητα των συγκεντρώσεων εισόδου και εξόδου οφείλεται στην προσέγγιση που κάναμε για να γράψουμε την Εξ. (1.9). (Η περίπτωση $\beta \ne 0$ εξετάζεται στην Άσκηση 1.1.)

Προσέξτε ότι αν στην παραπάνω περίπτωση, δηλαδή όταν $\beta \ll 1$, χρησιμοποιήσουμε την Εξ. (1.8) έχουμε:

$$\beta \frac{d}{d\tau }\tilde{C}=\left(1-\tilde{C}\right)-\beta \tilde{C}.$$

Αυτή δείχνει ότι η συγκέντρωση είναι περίπου, $\tilde{C}(\tau )\simeq 1$.