1.1 Τι είναι η Μαθηματική Μοντελοποίηση;
Τα μαθηματικά χρησιμοποιούνται εδώ και πολλές χιλιάδες χρόνια για τη μελέτη, την περιγραφή αλλά και την αξιοποίηση φαινομένων του φυσικού κόσμου που μας περιβάλλει, αλλά ακόμη και δημιουργημάτων της φαντασίας. Η μεγάλη χρησιμότητα των μαθηματικών προκύπτει από τη δυνατότητα, μέσω της χρήσης τους, να κάνουμε προβλέψεις για τα παραπάνω φαινόμενα, με άλλα λόγια να δημιουργούμε μοντέλα που αναπαριστούν τα υπό μελέτη φαινόμενα. Αυτός ακριβώς είναι ο στόχος της μαθηματικής μοντελοποίησης. Τι εννοούμε όμως με τον όρο «Μαθηματική Μοντελοποίηση»;
Ορισμός.
(Mathematical Modeling) είναι η ανάπτυξη μαθηματικής περιγραφής ενός φαινομένου, ενός συστήματος ή μιας διαδικασίας και η μελέτη τους με τη χρήση μαθηματικών εργαλείων. Τα εργαλεία αυτά μπορεί να είναι ένα σύστημα εξισώσεων, ένα σύνολο αριθμών, ένας αλγόριθμος, μια στοχαστική διαδικασία κλπ.
Με άλλα λόγια θα λέγαμε ότι Μαθηματική Μοντελοποίηση είναι η διαδικασία ανάπτυξης και η μελέτη ενός Μαθηματικού Μοντέλου.
Ορισμός.
(Mathematical Model) είναι η περιγραφή ενός φαινομένου, ενός συστήματος ή μιας διαδικασίας χρησιμοποιώντας μαθηματικές έννοιες και σύμβολα.
Η έννοια του φαινομένου, στον παραπάνω ορισμό, εμπεριέχει συστήματα από τελείως διαφορετικά επιστημονικά πεδία, όπως από τις φυσικές επιστήμες, τις επιστήμες της μηχανικής, τα οικονομικά, τις κοινωνικές επιστήμες αλλά και τις ανθρωπιστικές σπουδές. Ακριβώς λόγω του τεράστιου εύρους των πιθανών εφαρμογών, αντίστοιχα μεγάλος είναι και ο αριθμός των εν δυνάμει διαφορετικών μαθηματικών μοντέλων, όπως και των πιθανών μαθηματικών εργαλείων, τα οποία χρησιμοποιούνται για τη μελέτη και την επίλυση των μοντέλων.
Ας δούμε όμως, πιο συγκεκριμένα, τους στόχους ενός μαθηματικού μοντέλου. Πολύ συνοπτικά θα λέγαμε ότι οι στόχοι της μαθηματικής μοντελοποίησης ενός συγκεκριμένου συστήματος (φαινομένου) είναι οι εξής:
-
•
Η μελέτη και κατανόηση της συμπεριφοράς πολύπλοκων συστημάτων με τη χρήση των Μαθηματικών.
-
•
Η χρήση και η ανάπτυξη νέων, μαθηματικών εργαλείων που απαιτούνται για τη επίλυση ενός μοντέλου.
-
•
Η πρόβλεψη / προσομοίωση (prediction/simulation) συμπεριφορών και ιδιοτήτων πολύπλοκων συστημάτων μέσω των μαθηματικών μοντέλων.
-
•
Ο έλεγχος των υποθέσεων ενός μοντέλου και η αντίστοιχη βελτίωσή του.
Το τελευταίο είναι ιδιαίτερα σημαντικός καθώς δεν υπάρχει το «τέλειο μοντέλο»: Όλα τα μοντέλα βασίζονται σε ορισμένες υποθέσεις και ακόμη και το ότι ένα μοντέλο μπορεί να αναπαράγει δεδομένα αποτελέσματα σε συμφωνία με πειραματικές παρατηρήσεις, αυτό δεν σημαίνει ότι οι υποθέσεις/παραδοχές του μοντέλου είναι σωστές!
Γιατί όμως χρειαζόμαστε υποθέσεις/παραδοχές για κάθε μαθηματικό μοντέλο ενός πραγματικού φαινομένου; Πρώτον, επειδή όλα τα πραγματικά συστήματα – φαινόμενα είναι ιδιαίτερα πολύπλοκα και αποτελούνται ή περιγράφονται από ένα τεράστιο εύρος (ακόμη και άπειρο πολλές φορές) διαφορετικών παραμέτρων. Δεύτερον, κανένα μαθηματικό μοντέλο δεν μπορεί να συμπεριλάβει όλες αυτές τις παραμέτρους, οι οποίες πολλές φορές είναι επιπλέον άγνωστες. Η τρίτη και σημαντικότερη παρατήρηση είναι ότι δεν απαιτείται από το μοντέλο να συμπεριλαμβάνει όλες τις πιθανές παραμέτρους που επηρεάζουν ένα σύστημα αλλά μόνο τις πιο σημαντικές.
Όπως αναφέραμε το μοντέλο διατυπώνεται με τη χρήση πολύ διαφορετικών μαθηματικών εργαλείων ενώ μπορεί να περιγράφει και τελείως διαφορετικά συστήματα. Για το λόγο αυτά όλα τα μαθηματικά μοντέλα μπορούν να περιγραφούν σε διαφορετικές κατηγορίες, όπως:
-
•
Ανάλογα με το είδος των εξισώσεων που χρησιμοποιούνται: Μοντέλα συνεχών διαφορικών εξισώσεων, ή μερικών διαφορικών εξισώσεων.
-
•
Ντετερμινιστικά / Στοχαστικά μοντέλα: ανάλογα με ύπαρξη ή μη τυχαιότητας στο μοντέλο.
-
•
Διακριτά / Συνεχή μοντέλα ανάλογα με το είδος των μεταβλητών που ορίζονται.
-
•
Γραμμικά / Μη γραμμικά μοντέλα, ανάλογα με το αν οι μαθηματικές σχέσεις είναι γραμμικές ή όχι.
-
•
Χρόνο-εξαρτώμενα / Χρόνο-ανεξάρτητα ανάλογα με το αν οι παράμετροι του προβλήματος μεταβάλλονται με το χρόνο.
-
•
Μηχανιστικά / Περιγραφικά, ανάλογα με το αν προκύπτουν από βασικούς νόμους ή είναι περισσότερο μια ποιοτική περιγραφή του υπό μελέτη συστήματος
-
•
… κλπ.
1.1.1 Ιστορικά Στοιχεία
Ο ορισμός της μαθηματικής μοντελοποίησης που αναφέραμε παραπάνω είναι αρκετά γενικός και θα μπορούσε να συμπεριλάβει τη χρήση των μαθηματικών για τη μελέτη προβλημάτων, τα οποία σχετίζονται με συγκεκριμένα φαινόμενα, από την αρχαιότητα ακόμη.
Ως ένα από τα πρώτα πιο χαρακτηριστικά παραδείγματα μαθηματικής μοντελοποίησης αναφέρουμε τους νόμους του Νεύτωνα, οι οποίοι περιγράφουν τη δυναμική (χρονική εξέλιξη) μηχανικών συστημάτων που αποτελούνται από στερεά σώματα. Πιο σύγχρονα παραδείγματα αφορούν τη μελέτη βιολογικών συστημάτων, πολύπλοκων μοριακών υλικών και οικονομικών παραγώγων. Γενικά παραδείγματα μαθηματικής μοντελοποίησης είναι τα παρακάτω:
-
•
Κλασική μηχανική.
-
•
Κβαντική μηχανική.
-
•
Εξισώσεις που περιγράφουν Κυματικά φαινόμενα.
-
•
Μοντέλα που αφορούν βιολογικά συστήματα, ειδικότερα πληθυσμιακά μοντέλα τα οποία περιγράφουν την εξέλιξη των πληθυσμών βιολογικών ειδών.
-
•
Μοντέλα χρηματοοικονομίας.
-
•
Μοντέλα πολύπλοκων μοριακών υλικών σε διαφορετικές κλίμακες χωρικές και χρονικές.
-
•
κλπ.
Η παραπάνω λίστα είναι κυριολεκτικά χωρίς τέλος, καθώς στις μέρες μας μαθηματικά μοντέλα χρησιμοποιούνται για να περιγράψουν όλο και μεγαλύτερου εύρους φαινόμενα.
Εδώ χρειάζεται μια σημαντική διευκρίνηση. Η μαθηματική μελέτη πολύπλοκων φαινομένων – συστημάτων προϋποθέτει την ύπαρξη μαθηματικών σχέσεων, π.χ. εξισώσεων, οι οποίες περιγράφουν το υπό μελέτη σύστημα. Δεν υπάρχει όμως καμία καταρχήν απόδειξη περί της ύπαρξης τέτοιων σχέσεων. Επιπλέον, ακόμη και αν ο παρατηρητής υποθέσει ότι υπάρχουν τέτοιου τύπου μαθηματικοί νόμοι που μπορούν να περιγράψουν το φαινόμενο, δεν είναι βέβαιο ότι αυτές οι σχέσεις μπορούν να περιγράψουν πλήρως το υπό μελέτη σύστημα σε κάθε έκφανσή του.
Οι παραπάνω προβληματισμοί είναι ιδιαίτερα σημαντικοί αν αναλογιστούμε τη μεγάλη πολυπλοκότητα των πραγματικών συστημάτων. Μια διαφορετική προσέγγιση, σε σχέση με την αναζήτηση των απόλυτων νόμων, είναι η δημιουργία ενός μοντέλου που περιγράφει το σύστημα, το οποίο εμπεριέχει ένα μικρό αριθμό από τα πιο απαραίτητα στοιχεία του προβλήματος. Κατόπιν θα πρέπει να εξεταστεί η «αληθοφάνεια», η ικανότητα δηλαδή έγκυρων προβλέψεων του μοντέλου.
Τέλος θα πρέπει να τονίσουμε ότι πολλά μοντέλα είναι ιδιαίτερα επιτυχή, πέρα από την οποιαδήποτε αρχική ελπίδα. Χαρακτηριστικό παράδειγμα αποτελεί ή Κβαντική Μηχανική και ιδιαίτερα η εξίσωση του Schrödinger η οποία είναι ένα μαθηματικό μοντέλο περιγραφής της δυναμικής εξέλιξης των σωματιδίων σε μικροσκοπικό επίπεδο. Είναι ενδιαφέρον ότι ως σήμερα δεν υπάρχει ούτε ένα γνωστό παράδειγμα στο οποίο το συγκεκριμένο μοντέλο να αποτυγχάνει! Δεδομένης αυτής της επιτυχίας του μοντέλου, κάποιος μπορεί να ισχυρισθεί ότι πρόκειται για βασικό νόμο της φύσης! Το ίδιο συμβαίνει και με το 2ο Θερμοδυναμικό νόμο, ο οποίος έχει χαρακτηρισθεί ως νόμος, ακριβώς λόγω της γενικότητας του και της μη ύπαρξης παραδείγματος το οποίο να τον αντιβαίνει!
1.1.2 Διαδικασία Μαθηματικής Μοντελοποίησης
Τα κοινά σημεία των παραπάνω παραδειγμάτων αφορούν, πέρα από τη χρήση των μαθηματικών εργαλείων, τη μεθοδολογία προσέγγισης του υπό μελέτη φαινομένου – συστήματος.
Πιο συγκεκριμένα, θα περιγράφαμε τη διαδικασία της μαθηματικής μοντελοποίησης, ενός οποιουδήποτε φαινομένου, μέσα από τα παρακάτω βήματα:
-
a)
Βήμα 1: Συλλογή και οργάνωση δεδομένων, από πειραματικές μετρήσεις, για ένα συγκεκριμένο σύστημα – φαινόμενο.
-
b)
Βήμα 2: Δημιουργία ενός μαθηματικού μοντέλου του συστήματος, μέσω κατάλληλων υποθέσεων/παραδοχών.
-
c)
Βήμα 3: Επίλυση του μαθηματικού προβλήματος με τη χρήση υπαρχόντων, είτε με τη δημιουργία νέων, μαθηματικών εργαλείων.
-
d)
Βήμα 4: Έλεγχος των προβλέψεων του μοντέλου μέσω πειραματικών παρατηρήσεων.
-
e)
Βήμα 5: Αν οι προβλέψεις του μοντέλου δεν είναι ικανοποιητικές απαιτείται βελτίωση του μοντέλου και των υποθέσεων στις οποίες έχει βασισθεί και επανάληψη της διαδικασίας.
Η παραπάνω διαδικασία περιγράφεται στο σχήμα 1.1.
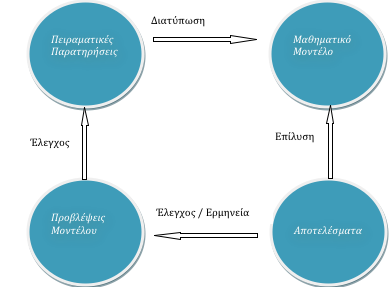
Ας δούμε πιο αναλυτικά μια περίπτωση και πιο συγκεκριμένα την ανάπτυξη της Κλασικής Μηχανικής. Κατά τη διάρκεια της ιστορίας έγιναν πολλές προσπάθειες να περιγράψουν του νόμους που διέπουν την κίνηση των σωμάτων. Αυτό ήταν ένα από τα προβλήματα για τα οποία υπήρχε πληθώρα διαθέσιμων δεδομένων από πειραματικές (κυρίως αστρονομικές) παρατηρήσεις (Βήμα 1). Το μαθηματικό μοντέλο, οι εξισώσεις δηλαδή που περιγράφουν τη δυναμική των σωμάτων, δημιουργήθηκε από την εργασία πολλών επιστημόνων, κυρίως του Νεύτωνα (Βήμα 2). Η ανάγκη επίλυσης των εξισώσεων αυτών οδήγησε στη δημιουργία νέων μαθηματικών εργαλείων και στην ανάπτυξη του απειροστικού λογισμού (Βήμα 3). Η ερμηνεία των αποτελεσμάτων του μοντέλου, ο έλεγχος των προβλέψεων του και η συμφωνία του σε σχέση με τις πειραματικές παρατηρήσεις (Βήμα 4 και 5), οδήγησε στην καθιέρωση του και στην περιγραφή του ως «νόμοι» της Κλασικής Μηχανικής, ή νόμοι του Νεύτωνα.
1.1.3 Παράμετροι / Μεταβλητές των Μοντέλων
Από τα βήματα που παρουσιάζονται παραπάνω, ιδιαίτερα σημαντικό είναι η δημιουργία του μαθηματικού μοντέλου, δηλαδή των κατάλληλων μαθηματικών μορφών – σχέσεων (εξισώσεων, αριθμών, κλπ.), οι οποίες περιγράφουν το πρόβλημα. Για να γίνει αυτό απαιτείται αρχικά να οριστούν οι μεταβλητές που περιγράφουν το φαινόμενο, δηλαδή οι παράμετροι του μοντέλου.
Χαρακτηριστικές παράμετροι σε ένα τυπικό μαθηματικό μοντέλο, μπορεί να είναι:
-
•
Οι θέσεις σωματιδίων σε μικροσκοπικό επίπεδο, ή φυσικών σωμάτων σε μακροσκοπικό (μοντέλα Φυσικών επιστημών).
-
•
Ο πληθυσμός ενός συγκεκριμένου βιολογικού είδους (σε Βιολογικά μοντέλα).
-
•
Οικονομικές μεταβλητές, όπως κόστος παραγωγής ή κέρδος (σε Οικονομικά μοντέλα).
-
•
Μεταβλητές που σχετίζονται με ανθρώπινες δραστηριότητες, παράδειγμα ποιότητα της ζωής σε μια μεγαλούπολη (σε μοντέλα Ανθρωπιστικών σπουδών).
-
•
κλπ.
Προσέξτε ότι στις περισσότερες από τις παραπάνω περιπτώσεις, οι μεταβλητές εξαρτώνται από το χρόνο και αυτό που ενδιαφέρει κυρίως είναι η πρόβλεψη της χρονικής τους εξάρτησης.
1.1.4 Μαθηματικά Εργαλεία
Όπως αναφέρθηκε και παραπάνω η επίλυση του μαθηματικού μοντέλου γίνεται με τη χρήση διάφορων μαθηματικών εργαλείων.
Χαρακτηριστικά παραδείγματα μαθηματικών εργαλείων είναι τα εξής:
-
•
Μέθοδοι επίλυσης γραμμικών εξισώσεων.
-
•
Μέθοδοι επίλυσης συνήθων και μερικών διαφορικών εξισώσεων, όπως χωρισμός μεταβλητών κλπ.
-
•
Μέθοδοι επίλυσης στοχαστικών εξισώσεων.
-
•
Αριθμητικές μέθοδοι επίλυσης ΣΔΕ, όπως Newton–Raphson, Runge–Kutta κλπ.
-
•
Αριθμητικές μέθοδοι επίλυσης ΜΔΕ, όπως πεπερασμένες διαφορές, πεπερασμένα στοιχεία, φασματικά στοιχεία, κλπ.
-
•
Μέθοδοι προσομοίωσης, όπως Μοριακή Δυναμική (Molecular Dynamics) και μέθοδοι Monte Carlo.
-
•
κλπ.