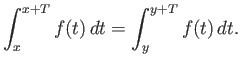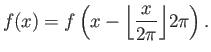Next: 2.3 Τριγωνομετρικά πολυώνυμα Up: 2. Τριγωνομετρικά πολυώνυμα Previous: 2.1 Μερικά βασικά περί Contents Index
Μια συνάρτηση
![]() ονομάζεται περιοδική με περίοδο
ονομάζεται περιοδική με περίοδο ![]() αν
αν
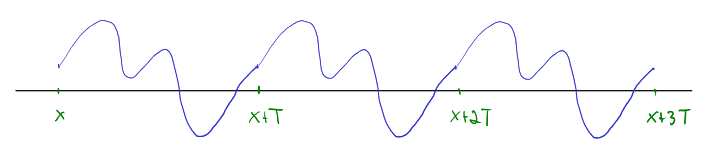
Σχήμα 2.2: Το γράφημα μιας περιοδικής συνάρτησης με περίοδο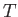
Για παράδειγμα η συνάρτηση ![]() είναι περιοδική με περίοδο
είναι περιοδική με περίοδο ![]() και η συνάρτηση
και η συνάρτηση
![]() είναι περιοδική με περίοδο 1.
είναι περιοδική με περίοδο 1.