2.1 Μερικά βασικά περί μιγαδικών αριθμών
Υποθέτουμε ως γνωστές τις βασικές έννοιες μιγαδικών αριθμών.
Οι μιγαδικοί αριθμοί είναι οι «αριθμοί» που μπορεί κανείς να γράψει στη μορφή
όπου
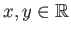 και το σύμβολο
και το σύμβολο 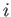 έχει την ιδιότητα
έχει την ιδιότητα 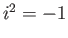
Οι ιδιότητες αυτές
αρκούν για να μας πουν πώς να επεκτείνουμε τις πράξεις της πρόσθεσης και του πολλαπλασιασμού
στους μιγαδικούς αριθμούς
έτσι ώστε να ισχύουν οι συνήθεις ιδιότητες των πράξεων.
Κάθε μιγαδικός αριθμός 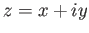 έχει ένα μέτρο
το
έχει ένα μέτρο
το
κι ένα όρισμα (εκτός το 0)
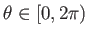 που είναι τέτοιο ώστε
που είναι τέτοιο ώστε
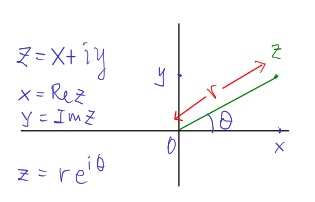
Σχήμα 2.1: Ο μιγαδικός αριθμός 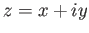 , με πραγματικό μέρος
, με πραγματικό μέρος
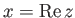 , φανταστικό μέρος
, φανταστικό μέρος
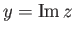 ,
μέτρο
,
μέτρο
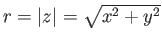 και όρισμα
και όρισμα 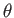 τέτοιο ώστε
τέτοιο ώστε
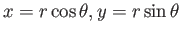
Ο μιγαδικός αριθμός
ονομάζεται συζυγής του 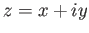 .
.
Η εκθετική συνάρτηση 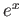 μπορεί να οριστεί και με μιγαδικό όρισμα από τη σειρά
μπορεί να οριστεί και με μιγαδικό όρισμα από τη σειρά
η οποία συγκλίνει για κάθε
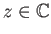 . Για τη συνάρτηση αυτή ισχύει
. Για τη συνάρτηση αυτή ισχύει
 .
Επίσης, αν
.
Επίσης, αν
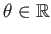 ισχύει ο τύπος
ισχύει ο τύπος
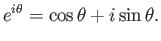 |
(2.1) |
Η πολική μορφή ενός μιγαδικού αριθμού 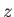 με μέτρο
με μέτρο 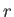 και όρισμα
και όρισμα 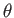 είναι
είναι
Από την (2.1) προκύπτουν εύκολα οι τύποι
οι οποίοι μας επιτρέπουν να εκφράσουμε τις τριγωνομετρικές συναρτήσεις με την εκθετική συνάρτηση, κάτι
που κάνει τους υπολογισμούς με αυτές τις συναρτήσεις πολύ ευκολότερους.
Για παράδειγμα, χρησιμοποιώντας τους άνω τύπους είναι πολύ εύκολο να υπολογίσει κανείς τα ημίτονα
και συνημίτονα για το άθροισμα δύο τόξων
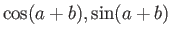 , χωρίς να χρειάζεται να θυμάται τους
τύπους.
, χωρίς να χρειάζεται να θυμάται τους
τύπους.
Άσκηση 2.1
Χρησιμοποιώντας τους τύπους (2.2) βρείτε τύπους για τα
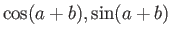 μέσω των τριγωνομετρικών αριθμών των
μέσω των τριγωνομετρικών αριθμών των 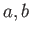 .
.
Υπόδειξη: Ποιο το πραγματικό και ποιο το φανταστικό μέρος του
 ;
;
Άσκηση 2.2
Λέμε ότι μια ακολουθία
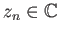 συγκλίνει στο
συγκλίνει στο
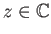 αν
αν
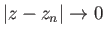 όταν
όταν
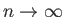 .
Δείξτε ότι
.
Δείξτε ότι 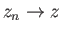 αν και μόνο αν
αν και μόνο αν
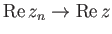 και
και
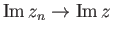 .
.
Mihalis Kolountzakis
2015-11-28
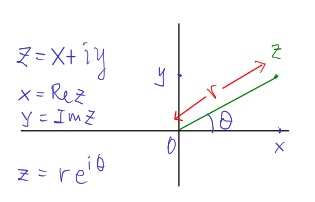
, με πραγματικό μέρος
, φανταστικό μέρος
, μέτρο
και όρισμα
τέτοιο ώστε
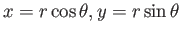
![]() μπορεί να οριστεί και με μιγαδικό όρισμα από τη σειρά
μπορεί να οριστεί και με μιγαδικό όρισμα από τη σειρά
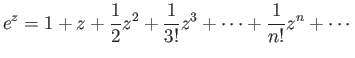
![]() ;
;