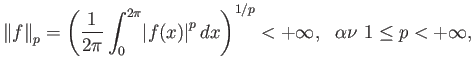3.4 Ο κύκλος
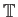 . Οι χώροι συναρτήσεων
. Οι χώροι συναρτήσεων
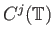 και
και
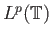
Οι συναρτήσεις
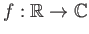 των οποίων παίρνουμε τους συντελεστές Fourier
είναι πάντα
των οποίων παίρνουμε τους συντελεστές Fourier
είναι πάντα  -περιοδικές και πρέπει επίσης να είναι ολοκληρώσιμες στο διάστημα
-περιοδικές και πρέπει επίσης να είναι ολοκληρώσιμες στο διάστημα
![$ [0,2\pi]$](img394.png) .
.
Άσκηση 3.16
Δείξτε ότι μια  -περιοδική συνάρτηση που είναι ολοκληρώσιμη στο
-περιοδική συνάρτηση που είναι ολοκληρώσιμη στο ![$ [0,2\pi]$](img394.png) δε μπορεί
να είναι ολοκληρώσιμη και στο
δε μπορεί
να είναι ολοκληρώσιμη και στο
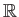 εκτός αν είναι ίση με μηδέν σχεδόν παντού.
εκτός αν είναι ίση με μηδέν σχεδόν παντού.
Σημαντική ειδική περίπτωση αυτών είναι οι συνεχείς  -περιοδικές συναρτήσεις, αφού κάθε συνεχής
συνάρτηση είναι ολοκληρώσιμη σε οποιοδήποτε φραγμένο κλειστό διάστημα αφού είναι φραγμένη σε αυτό.
-περιοδικές συναρτήσεις, αφού κάθε συνεχής
συνάρτηση είναι ολοκληρώσιμη σε οποιοδήποτε φραγμένο κλειστό διάστημα αφού είναι φραγμένη σε αυτό.
Ορισμός 3.1
Θα λέμε ότι μια συνάρτηση ανήκει στο χώρο
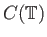 αν είναι συνεχής σε όλο το
αν είναι συνεχής σε όλο το
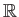 και
και  -περιοδική.
Θα λέμε γενικότερα ότι μια συνάρτηση ανήκει στο χώρο
-περιοδική.
Θα λέμε γενικότερα ότι μια συνάρτηση ανήκει στο χώρο
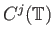 ,
,
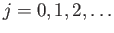 αν είναι
αν είναι
 -περιοδική και η
-περιοδική και η 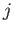 -τάξης παράγωγός της υπάρχει και είναι συνεχής παντού.
(Ως μηδενικής τάξης παράγωγος της
-τάξης παράγωγός της υπάρχει και είναι συνεχής παντού.
(Ως μηδενικής τάξης παράγωγος της  θεωρείται η ίδια η
θεωρείται η ίδια η  .)
.)
Εν γένει αν 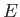 είναι ένα σύνολο πάνω στν οποίο ορίζονται συναρτήσεις (με πραγματικές ή μιγαδικές τιμές)
τότε με
είναι ένα σύνολο πάνω στν οποίο ορίζονται συναρτήσεις (με πραγματικές ή μιγαδικές τιμές)
τότε με 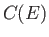 συμβολίζουμε εκείνες τις συναρτήσεις που είναι συνεχείς. Για να υπάρχει κάποια
συμβατότητα αυτού του γενικού ορισμού με τον ορισμό για το
συμβολίζουμε εκείνες τις συναρτήσεις που είναι συνεχείς. Για να υπάρχει κάποια
συμβατότητα αυτού του γενικού ορισμού με τον ορισμό για το
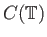 που δώσαμε παραπάνω θα πρέπει
κατ' αρχήν να δώσουμε ένα νόημα στο σύμβολο
που δώσαμε παραπάνω θα πρέπει
κατ' αρχήν να δώσουμε ένα νόημα στο σύμβολο
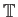 , να ορίσουμε δηλ. ένα χώρο τέτοιο ώστε
οι συνεχείς συναρτήσεις πάνω σε αυτόν να «είναι» οι
, να ορίσουμε δηλ. ένα χώρο τέτοιο ώστε
οι συνεχείς συναρτήσεις πάνω σε αυτόν να «είναι» οι  -περιοδικές συναρτήσεις πάνω στο
-περιοδικές συναρτήσεις πάνω στο
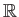 που είναι συνεχείς.
που είναι συνεχείς.
Ο χώρος
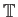 (που τον ονομάζουμε και κύκλο και μιλάμε συχνά για συνεχείς συναρτήσεις
πάνω στον κύκλο όταν θέλουμε να μιλήσουμε για συνεχείς και περιοδικές συναρτήσεις) ορίζεται
να είναι εκείνος ο τοπολογικός χώρος που προκύπτει αν ορίσουμε τη σχέση ισοδυναμίας πάνω στο
(που τον ονομάζουμε και κύκλο και μιλάμε συχνά για συνεχείς συναρτήσεις
πάνω στον κύκλο όταν θέλουμε να μιλήσουμε για συνεχείς και περιοδικές συναρτήσεις) ορίζεται
να είναι εκείνος ο τοπολογικός χώρος που προκύπτει αν ορίσουμε τη σχέση ισοδυναμίας πάνω στο
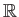
(όπου με
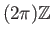 συμβολίζουμε όλα τα ακέραια πολλαπλάσια του
συμβολίζουμε όλα τα ακέραια πολλαπλάσια του  ) και κατόπιν
ταυτίσουμε μεταξύ τους όλα τα ισοδύναμα στοιχεία. Εύκολα βλέπει κανείς ότι η κλάση ισοδυναμίας
του
) και κατόπιν
ταυτίσουμε μεταξύ τους όλα τα ισοδύναμα στοιχεία. Εύκολα βλέπει κανείς ότι η κλάση ισοδυναμίας
του
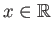 είναι οι αριθμοί
είναι οι αριθμοί 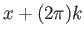 ,
,
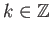 , οπότε ανά δύο τα στοιχεία του
, οπότε ανά δύο τα στοιχεία του 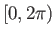 δεν
είναι μεταξύ τους ισοδύναμα και κάθε κλάση ισοδυναμίας έχει μοναδικό αντιπρόσωπο στο
δεν
είναι μεταξύ τους ισοδύναμα και κάθε κλάση ισοδυναμίας έχει μοναδικό αντιπρόσωπο στο 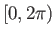 .
Οι δε αριθμοί 0 και
.
Οι δε αριθμοί 0 και  είναι μεταξύ τους ισοδύναμοι και άρα μπορούμε να βλέπουμε το χώρο
είναι μεταξύ τους ισοδύναμοι και άρα μπορούμε να βλέπουμε το χώρο
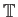 ως ένα κύκλο ή, με άλλα λόγια, να βλέπουμε το χώρο
ως ένα κύκλο ή, με άλλα λόγια, να βλέπουμε το χώρο
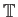 ως το
ως το ![$ [0,2\pi]$](img394.png) όπου όμως τα σημεία 0
και
όπου όμως τα σημεία 0
και  είναι ίδια και αν κινηθούμε από τα αριστερά προς το
είναι ίδια και αν κινηθούμε από τα αριστερά προς το  τότε μόλις το περάσουμε
βρισκόμαστε στα δεξιά του 0.
τότε μόλις το περάσουμε
βρισκόμαστε στα δεξιά του 0.
Είναι φανερό ότι κάθε συνεχής και  -περιοδική συνάρτηση
-περιοδική συνάρτηση
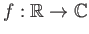 ορίζει μια συνεχή συνάρτηση
πάνω στο χώρο
ορίζει μια συνεχή συνάρτηση
πάνω στο χώρο
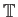 και αντίστροφα. Γι' αυτό και χρησιμοποιούμε το σύμβολο
και αντίστροφα. Γι' αυτό και χρησιμοποιούμε το σύμβολο
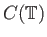 .
.
Ένας εναλλακτικός τρόπος να βλέπει κανείς τις συναρτήσεις που είναι ορισμένες πάνω στο
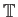 είναι να τις βλέπει ως συναρτήσεις πάνω στο μοναδιαίο κύκλο στο μιγαδικό επίπεδο
είναι να τις βλέπει ως συναρτήσεις πάνω στο μοναδιαίο κύκλο στο μιγαδικό επίπεδο
Πράγματι, εύκολα βλέπει κανείς ότι μια συνάρτηση
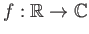 είναι μια συνάρτηση ορισμένη πάνω στο
είναι μια συνάρτηση ορισμένη πάνω στο
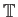 αν και μόνο αν αυτή η συνάρτηση είναι της μορφής
αν και μόνο αν αυτή η συνάρτηση είναι της μορφής
για κάποια συνάρτηση 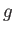 ορισμένη πάνω στο μοναδιαίο κύκλο του μιγαδικού επιπέδου.
Ειδικότερα για το χώρο
ορισμένη πάνω στο μοναδιαίο κύκλο του μιγαδικού επιπέδου.
Ειδικότερα για το χώρο
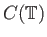 μπορεί κανείς να βλέπει τα στοιχεία του ως τις
συνεχείς συναρτήσεις πάνω στο μοναδιαίο κύκλο.
μπορεί κανείς να βλέπει τα στοιχεία του ως τις
συνεχείς συναρτήσεις πάνω στο μοναδιαίο κύκλο.
Όμως όποιος δυσκολεύται να κατανοήσει τις τοπολογικές έννοιες που αναφέρουμε πιο πάνω μπορεί
να κρατήσει τον Ορισμό 3.1 ο οποίος αρκεί για να δώσει
νόημα σε όλες τις προτάσεις που θα μας απασχολήσουν.
Εντελώς αντίστοιχα ορίζουμε το σημαίνει να ανήκει μια συνάρτηση  στο χώρο
στο χώρο
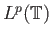 .
Μια τέτοια συνάρτηση πρέπει να είναι
.
Μια τέτοια συνάρτηση πρέπει να είναι  -περιοδική και να ισχύει
-περιοδική και να ισχύει
και
Όπως και στους συνηθισμένους χώρους 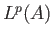 (δείτε Κεφάλαιο 1)
το εύρος του
(δείτε Κεφάλαιο 1)
το εύρος του 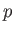 είναι το διάστημα
είναι το διάστημα
![$ [1, +\infty]$](img722.png) , αλλιώς η νόρμα
, αλλιώς η νόρμα
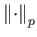 που ορίζεται παραπάνω
δεν ικανοποιεί την τριγωνική ανισότητα και άρα δε μπορεί να χρησιμεύσει ως έννοια απόστασης ανάμεσα
σε δύο συναρτήσεις
που ορίζεται παραπάνω
δεν ικανοποιεί την τριγωνική ανισότητα και άρα δε μπορεί να χρησιμεύσει ως έννοια απόστασης ανάμεσα
σε δύο συναρτήσεις
Επίσης όμοια με τους χώρους 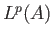 δεν ξεχωρίζουμε μεταξύ τους δύο συναρτήσεις
δεν ξεχωρίζουμε μεταξύ τους δύο συναρτήσεις  και
και 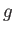 οι οποίες
είναι ίδιες σχεδόν παντού, διαφέρουν δηλ. σε ένα σύνολο
οι οποίες
είναι ίδιες σχεδόν παντού, διαφέρουν δηλ. σε ένα σύνολο 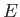 με μέτρο Lebesgue
με μέτρο Lebesgue 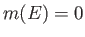 .
.
Mihalis Kolountzakis
2015-11-28
![]() των οποίων παίρνουμε τους συντελεστές Fourier
είναι πάντα
των οποίων παίρνουμε τους συντελεστές Fourier
είναι πάντα ![]() -περιοδικές και πρέπει επίσης να είναι ολοκληρώσιμες στο διάστημα
-περιοδικές και πρέπει επίσης να είναι ολοκληρώσιμες στο διάστημα
![]() .
.
![]() είναι ένα σύνολο πάνω στν οποίο ορίζονται συναρτήσεις (με πραγματικές ή μιγαδικές τιμές)
τότε με
είναι ένα σύνολο πάνω στν οποίο ορίζονται συναρτήσεις (με πραγματικές ή μιγαδικές τιμές)
τότε με ![]() συμβολίζουμε εκείνες τις συναρτήσεις που είναι συνεχείς. Για να υπάρχει κάποια
συμβατότητα αυτού του γενικού ορισμού με τον ορισμό για το
συμβολίζουμε εκείνες τις συναρτήσεις που είναι συνεχείς. Για να υπάρχει κάποια
συμβατότητα αυτού του γενικού ορισμού με τον ορισμό για το
![]() που δώσαμε παραπάνω θα πρέπει
κατ' αρχήν να δώσουμε ένα νόημα στο σύμβολο
που δώσαμε παραπάνω θα πρέπει
κατ' αρχήν να δώσουμε ένα νόημα στο σύμβολο
![]() , να ορίσουμε δηλ. ένα χώρο τέτοιο ώστε
οι συνεχείς συναρτήσεις πάνω σε αυτόν να «είναι» οι
, να ορίσουμε δηλ. ένα χώρο τέτοιο ώστε
οι συνεχείς συναρτήσεις πάνω σε αυτόν να «είναι» οι ![]() -περιοδικές συναρτήσεις πάνω στο
-περιοδικές συναρτήσεις πάνω στο
![]() που είναι συνεχείς.
που είναι συνεχείς.
![]() (που τον ονομάζουμε και κύκλο και μιλάμε συχνά για συνεχείς συναρτήσεις
πάνω στον κύκλο όταν θέλουμε να μιλήσουμε για συνεχείς και περιοδικές συναρτήσεις) ορίζεται
να είναι εκείνος ο τοπολογικός χώρος που προκύπτει αν ορίσουμε τη σχέση ισοδυναμίας πάνω στο
(που τον ονομάζουμε και κύκλο και μιλάμε συχνά για συνεχείς συναρτήσεις
πάνω στον κύκλο όταν θέλουμε να μιλήσουμε για συνεχείς και περιοδικές συναρτήσεις) ορίζεται
να είναι εκείνος ο τοπολογικός χώρος που προκύπτει αν ορίσουμε τη σχέση ισοδυναμίας πάνω στο
![]()
![]() -περιοδική συνάρτηση
-περιοδική συνάρτηση
![]() ορίζει μια συνεχή συνάρτηση
πάνω στο χώρο
ορίζει μια συνεχή συνάρτηση
πάνω στο χώρο
![]() και αντίστροφα. Γι' αυτό και χρησιμοποιούμε το σύμβολο
και αντίστροφα. Γι' αυτό και χρησιμοποιούμε το σύμβολο
![]() .
.
![]() είναι να τις βλέπει ως συναρτήσεις πάνω στο μοναδιαίο κύκλο στο μιγαδικό επίπεδο
είναι να τις βλέπει ως συναρτήσεις πάνω στο μοναδιαίο κύκλο στο μιγαδικό επίπεδο
![]() στο χώρο
στο χώρο
![]() .
Μια τέτοια συνάρτηση πρέπει να είναι
.
Μια τέτοια συνάρτηση πρέπει να είναι ![]() -περιοδική και να ισχύει
-περιοδική και να ισχύει