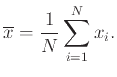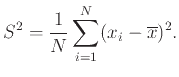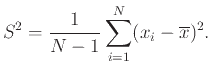12.3 Διασπορά μιας ΤΜ και ανισότητες απόκλισης
Ορισμός 12.7
(Διασπορά μιας τυχαίας μεταβλητής)
Αν  είναι μια ΤΜ με μέση τιμή
είναι μια ΤΜ με μέση τιμή
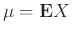 τότε η διασπορά της
τότε η διασπορά της  είναι
η ποσότητα
είναι
η ποσότητα
![$ {\mathbb{V}ar}\left[X\right] = \sigma^2(X) = {\bf E}{(X-\mu)^2}$](img2728.png) . Ορίζουμε επίσης την τυπική απόκλιση της
. Ορίζουμε επίσης την τυπική απόκλιση της  ως την ποσότητα
ως την ποσότητα
![$ \sigma(X) = \sqrt{{\mathbb{V}ar}\left[X\right]}$](img2729.png) .
.
Παρατήρηση 12.14
Από τον Ορισμό 12.7 γίνεται φανερό ότι η διασπορά και η τυπική απόκλιση μιας ΤΜ
μετρούν το πόσο πιθανό είναι να αποκλίνει η ΤΜ  από τη μέση τιμή της.
από τη μέση τιμή της.
Παρατήρηση 12.15
Επειδή η ΤΜ
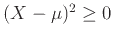 η διασπορά της
η διασπορά της  υπάρχει πάντα και είναι πεπερασμένος
μη αρνητικός αριθμός ή
υπάρχει πάντα και είναι πεπερασμένος
μη αρνητικός αριθμός ή 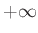 , υπό την προϋπόθεση μόνο
ότι η
, υπό την προϋπόθεση μόνο
ότι η  έχει μέση τιμή, δηλ.
έχει μέση τιμή, δηλ.
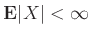 .
.
Άσκηση 12.29
Δείξτε ότι αν 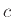 είναι σταθερά τότε
είναι σταθερά τότε
![$ {\mathbb{V}ar}\left[X-c\right] = {\mathbb{V}ar}\left[X\right] = {\mathbb{V}ar}\left[-X\right]$](img2738.png) .
.
Άσκηση 12.30
Δείξτε ότι αν
![$ {\mathbb{V}ar}\left[X\right] = 0$](img2739.png) τότε
τότε
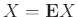 σχεδόν σίγουρα.
σχεδόν σίγουρα.
Παράδειγμα 12.20
Αν η  είναι ομοιόμορφα κατανεμημένη στο
είναι ομοιόμορφα κατανεμημένη στο
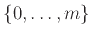 τότε
τότε
χρησιμοποιώντας το αποτέλεσμα του Προβλήματος 1.14.
Επίσης
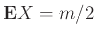 αφού η πυκνότητα της
αφού η πυκνότητα της  είναι συμμετρική γύρω από το
είναι συμμετρική γύρω από το 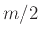 .
Οπότε, χρησιμοποιώντας τον τύπο του Προβλήματος 12.28
έχουμε
.
Οπότε, χρησιμοποιώντας τον τύπο του Προβλήματος 12.28
έχουμε
Θεώρημα 12.5
Αν οι ΤΜ
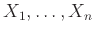 είναι ανεξάρτητες ανά δύο και έχουν μέση τιμή τότε
είναι ανεξάρτητες ανά δύο και έχουν μέση τιμή τότε
Απόδειξη.
Ας είναι
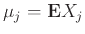
,
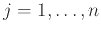
.
Η μέση τιμή της
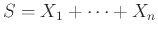
υπάρχει και ισούται με
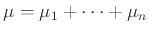
, οπότε
Η απόδειξη τελειώνει με την παρατήρηση ότι
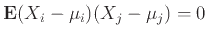
αν
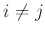
,
αφού οι ΤΜ
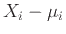
και
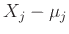
είναι ανεξάρτητες και έχουν μέση τιμή
0.

Απόδειξη.
Ορίζουμε το ενδεχόμενο
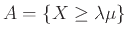
.
Αν
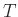
είναι το σύνολο τιμών της

τότε, από τον ορισμό της
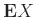
, έχουμε
Η ανισότητα προκύπτει αφού διαρέσουμε δια του
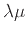
.

Πόρισμα 12.1
(Ανισότητα Chebyshev)
Αν η  έχει πεπερασμένη διασπορά
έχει πεπερασμένη διασπορά 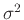 και μέση τιμή
και μέση τιμή 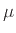 τότε
τότε
Απόδειξη.
Ορίζουμε τη μη-αρνητική ΤΜ
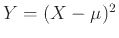
με
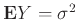
και εφαρμόζουμε σε αυτή την ανισότητα του Markov
(Θεώρημα
12.6). Παίρνουμε

Άσκηση 12.31
(Γενικευμένη ανισότητα Chebyshev)
Έστω
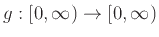 μια αυστηρά αύξουσα συνάρτηση και
μια αυστηρά αύξουσα συνάρτηση και  μια ΤΜ τέτοια
ώστε
μια ΤΜ τέτοια
ώστε
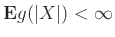 .
Δείξτε ότι
.
Δείξτε ότι
Άσκηση 12.32 (Ακολουθούμε το συμβολισμό και ορολογία του Παραδείγματος
12.19.)
Χρησιμοποιήστε την ανισότητα του Chebyshev για να βρείτε ένα άνω φράγμα
για την
![$ {{\bf {Pr}}\left[{{\left\vert{S_n}\right\vert} > n/10}\right]}$](img2777.png) .
.
Άσκηση 12.33
Έστω  μια ΤΜ που ακολουθεί τη γεωμετρική κατανομή (12.2) με παράμετρο
μια ΤΜ που ακολουθεί τη γεωμετρική κατανομή (12.2) με παράμετρο 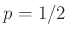 .
Βρείτε άνω φράγματα για την ποσότητα
.
Βρείτε άνω φράγματα για την ποσότητα
![$ {{\bf {Pr}}\left[{X\ge 10}\right]}$](img2779.png) χρησιμοποιώντας την ανισότητα Markov και
την ανισότητα του Chebyshev και συγκρίνετέ τα μεταξύ τους καθώς και με την ακριβή τιμή γι' αυτή
την ποσότητα.
χρησιμοποιώντας την ανισότητα Markov και
την ανισότητα του Chebyshev και συγκρίνετέ τα μεταξύ τους καθώς και με την ακριβή τιμή γι' αυτή
την ποσότητα.
Άσκηση 12.34
Ας υποθέσουμε ότι έχουμε ένα μεγάλο πληθυσμό ανθρώπων του οποίου θέλουμε να εκτιμήσουμε το μέσο ύψος
αλλά και το πόσο αυτό κυμαίνεται μέσα στον πληθυσμό. Λίγο πιο αυστηρά, θέλουμε να εκτιμήσουμε τη μέση τιμή
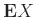 και τη διασπορά
και τη διασπορά
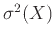 της τυχαίας μεταβλητής
της τυχαίας μεταβλητής  που προκύπτει
αν επιλέξουμε ένα τυχαίο άτομο και μετρήσουμε το ύψος του, με όλα τα άτομα εξίσου πιθανά να επιλεγούν.
που προκύπτει
αν επιλέξουμε ένα τυχαίο άτομο και μετρήσουμε το ύψος του, με όλα τα άτομα εξίσου πιθανά να επιλεγούν.
Ο τρόπος που το κάνουμε είναι να διαλέξουμε 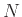 φορές τυχαία (
φορές τυχαία (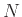 μεγάλο) ένα άτομο και να μετρήσουμε το ύψος του,
έστω
μεγάλο) ένα άτομο και να μετρήσουμε το ύψος του,
έστω
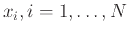 . Έπειτα εκτιμούμε το μέσο ύψος του πληθυσμού από την ποσότητα
. Έπειτα εκτιμούμε το μέσο ύψος του πληθυσμού από την ποσότητα
Θυμόμαστε τώρα το γενικό ορισμό
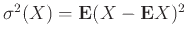 και εκτιμούμε ανάλογα τη διασπορά του ύψους από την ποσότητα
και εκτιμούμε ανάλογα τη διασπορά του ύψους από την ποσότητα
Όμως ο στατιστικός φίλος μας, στον οποίο δείχνουμε τη μέθοδό μας, ισχυρίζεται ότι δεν πρέπει να το κάνουμε έτσι αλλά ως εξής:
Η αλήθεια είναι ότι αυτές οι δύο ποσότητες ελάχιστα διαφέρουν μεταξύ τους όταν το 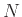 είναι μεγάλο. Όμως ποιος έχει δίκιο;
είναι μεγάλο. Όμως ποιος έχει δίκιο;
Mihalis Kolountzakis
2015-11-28
![]() , όπου
, όπου
![]() και
και ![]() .
Δείξτε ότι
.
Δείξτε ότι
![]() και
και
![]() .
.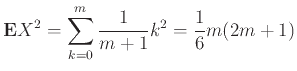
![$\displaystyle {\mathbb{V}ar}\left[X\right] = \frac{1}{6}m(2m+1) - \frac{m^2}{4} = \frac{m(m+2)}{12}.
$](img2742.png)
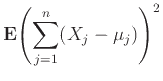
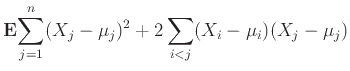
![$\displaystyle \sum_{j=1}^n {\mathbb{V}ar}\left[X_j\right] + 2 \sum_{i<j} {\bf E}{ (X_i-\mu_i)(X_j - \mu_j) }.$](img2751.png)
![$\displaystyle \sum_{t \in T} t {{\bf {Pr}}\left[{X = t}\right]}$](img2762.png)
![$\displaystyle \sum_{t \in T, t < \lambda\mu} t {{\bf {Pr}}\left[{X = t}\right]} + \sum_{t \in T, t \ge \lambda\mu} t {{\bf {Pr}}\left[{X = t}\right]}$](img2763.png)
![$\displaystyle \sum_{t \in T, t \ge \lambda\mu} t {{\bf {Pr}}\left[{X = t}\right]}$](img2764.png)
![$\displaystyle \sum_{t \in T, t \ge \lambda\mu} \lambda\mu {{\bf {Pr}}\left[{X = t}\right]}$](img2765.png)
![$\displaystyle {{\bf {Pr}}\left[{ {\left\vert{X-\mu}\right\vert} \ge \lambda \si...
...= {{\bf {Pr}}\left[{Y \ge \lambda^2 \sigma^2}\right]} \le \frac{1}{\lambda^2}.
$](img2773.png)
![$\displaystyle {{\bf {Pr}}\left[{{\left\vert{X}\right\vert} \ge \lambda}\right]} \le \frac{{\bf E}{g({\left\vert{X}\right\vert})}}{g(\lambda)}.
$](img2776.png)
![]() φορές τυχαία (
φορές τυχαία (![]() μεγάλο) ένα άτομο και να μετρήσουμε το ύψος του,
έστω
μεγάλο) ένα άτομο και να μετρήσουμε το ύψος του,
έστω
![]() . Έπειτα εκτιμούμε το μέσο ύψος του πληθυσμού από την ποσότητα
. Έπειτα εκτιμούμε το μέσο ύψος του πληθυσμού από την ποσότητα