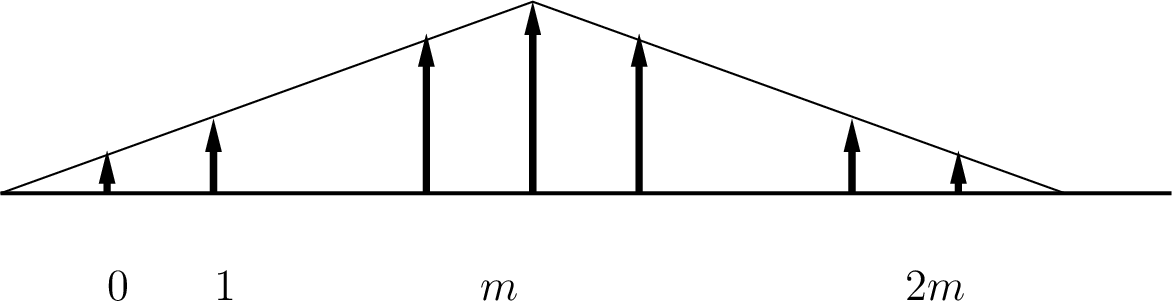
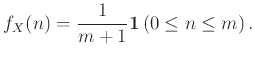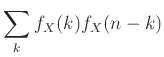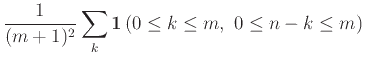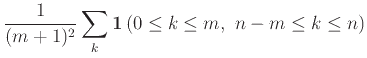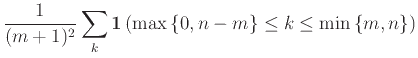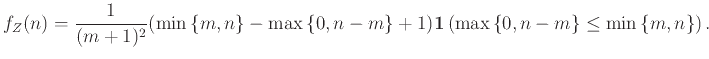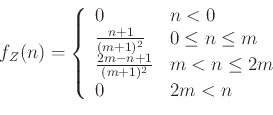12.1 Τυχαίες μεταβλητές και η κατανομή τους
Παράδειγμα 12.1
Ας υποθέσουμε ότι ρίχνουμε δύο φορές ένα συνηθισμένο ζάρι, και συμβολίζουμε με 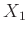 το αποτέλεσμα της 1ης ρίψης (
το αποτέλεσμα της 1ης ρίψης (
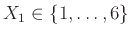 ) και
) και 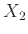 το αποτέλεσμα της
2ης ρίψης. Ορίζουμε ακόμη
το αποτέλεσμα της
2ης ρίψης. Ορίζουμε ακόμη 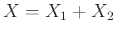 να είναι το άθροισμα των δύο ρίψεων.
Οι ποσότητες
να είναι το άθροισμα των δύο ρίψεων.
Οι ποσότητες
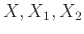 εν γένει αλλάζουν κάθε φορά που πραγματοποιείται
το πείραμα. Τέτοιες ποσότητες, των οποίων η τιμή εξαρτάται από την έκβαση κάποιου πειράματος,
τις ονομάζουμε τυχαίες μεταβλητές.
εν γένει αλλάζουν κάθε φορά που πραγματοποιείται
το πείραμα. Τέτοιες ποσότητες, των οποίων η τιμή εξαρτάται από την έκβαση κάποιου πειράματος,
τις ονομάζουμε τυχαίες μεταβλητές.
Αριθμήσιμο ονομάζεται ένα σύνολο 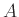 αν υπάρχει επί συνάρτηση
αν υπάρχει επί συνάρτηση
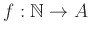 από το σύνολο
των φυσικών αριθμών επί του
από το σύνολο
των φυσικών αριθμών επί του 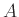 .
Με άλλα λόγια, το
.
Με άλλα λόγια, το 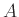 είναι αριθμήσιμο αν μπορούμε να βρούμε μια ακολουθία
είναι αριθμήσιμο αν μπορούμε να βρούμε μια ακολουθία
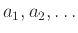 που περιέχει όλα τα στοιχεία του.
που περιέχει όλα τα στοιχεία του.
Είναι προφανές ότι κάθε πεπερασμένο σύνολο είναι αριθμήσιμο.
Επίσης αριθμήσιμα σύνολα είναι οι φυσικοί αριθμοί
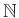 , οι ακέραιοι
, οι ακέραιοι
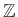 , οι ρητοί
, οι ρητοί
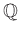 ,
καρτεσιανά γινόμενα
,
καρτεσιανά γινόμενα
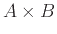 , όπου τα
, όπου τα 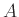 και
και 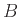 είναι αριθμήσιμα, και άπειρες ενώσεις
του τύπου
είναι αριθμήσιμα, και άπειρες ενώσεις
του τύπου
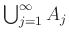 , όπου τα
, όπου τα 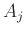 είναι αριθμήσιμα.
είναι αριθμήσιμα.
Σύνολα που δεν είναι αριθμήσιμα είναι π.χ. το
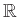 ή ένα διάστημα
ή ένα διάστημα 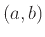 .
.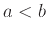 .
Αυτό το τελευταίο δεν είναι προφανές και θέλει απόδειξη, την οποία δε θα δώσουμε εδώ.
.
Αυτό το τελευταίο δεν είναι προφανές και θέλει απόδειξη, την οποία δε θα δώσουμε εδώ.
Μπορείτε επίσης να συμβουλευτείτε την §1.8 αυτών των σημειώσεων.
Παρατήρηση 12.1
Εύκολα βλέπει κανείς (χρησιμοποιώντας το γεγονός ότι καρτεσιανά γινόμενα αριθμησίμων συνόλων
με πεπερασμένους σε πλήθος παράγοντες είναι επίσης αριθμήσιμα)
ότι αν
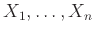 είναι διακριτές ΤΜ και
είναι διακριτές ΤΜ και
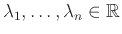 τότε
η ΤΜ
τότε
η ΤΜ
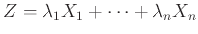 είναι επίσης διακριτή.
Έτσι μπορούμε ελεύθερα να μιλάμε για πεπερασμένους γραμμικούς συνδυασμούς διακριτών ΤΜ γνωρίζοντας
εκ των προτέρων ότι κι αυτοί είναι διακριτές ΤΜ.
είναι επίσης διακριτή.
Έτσι μπορούμε ελεύθερα να μιλάμε για πεπερασμένους γραμμικούς συνδυασμούς διακριτών ΤΜ γνωρίζοντας
εκ των προτέρων ότι κι αυτοί είναι διακριτές ΤΜ.
Κάτι τέτοιο δεν ισχύει για άπειρους γραμμικούς συνδυασμούς από ΤΜ.
Για παράδειγμα, αν 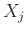 ,
,
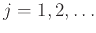 , είναι ΤΜ τέτοιες ώστε η
, είναι ΤΜ τέτοιες ώστε η 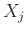 έχει σύνολο τιμών
το
έχει σύνολο τιμών
το
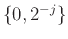 , τότε η ΤΜ
, τότε η ΤΜ
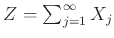 ορίζεται χωρίς πρόβλημα
αφού η σειρά πάντα συγκλίνει, ότι τιμές και να έχουν τα
ορίζεται χωρίς πρόβλημα
αφού η σειρά πάντα συγκλίνει, ότι τιμές και να έχουν τα 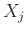 , αλλά μπορεί εν δυνάμει (για παράδειγμα
όταν όλες οι
, αλλά μπορεί εν δυνάμει (για παράδειγμα
όταν όλες οι 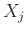 είναι ανεξάρτητες - δείτε παρακάτω τον Ορισμό 12.4
για τον ορισμό της ανεξαρτησίας ΤΜ) να πάρει
οποιονδήποτε πραγματικό αριθμό του διαστήματος
είναι ανεξάρτητες - δείτε παρακάτω τον Ορισμό 12.4
για τον ορισμό της ανεξαρτησίας ΤΜ) να πάρει
οποιονδήποτε πραγματικό αριθμό του διαστήματος 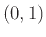 ως τιμή. Πράγματι, αν
ως τιμή. Πράγματι, αν
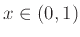 τότε,
γράφοντας τον
τότε,
γράφοντας τον 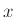 στο δυαδικό του ανάπτυγμα
στο δυαδικό του ανάπτυγμα
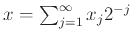 , με
, με
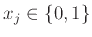 ,
βλέπουμε ότι είναι δυνατό να έχουμε
,
βλέπουμε ότι είναι δυνατό να έχουμε 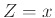 φτάνει να πάρουν οι
φτάνει να πάρουν οι 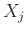 τις κατάλληλες τιμές.
τις κατάλληλες τιμές.
Παράδειγμα 12.2
Στο Παράδειγμα 12.1 οι ΤΜ που ορίσαμε είναι όλες αριθμητικές και διακριτές.
Η ΤΜ
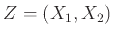 έχει σύνολο τιμών το
έχει σύνολο τιμών το
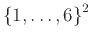 και είναι διανυσματική ΤΜ.
και είναι διανυσματική ΤΜ.
Παράδειγμα 12.3
Ας υποθέσουμε ότι παρατηρούμε μια καταιγίδα και καταγράφουμε τη χρονική στιγμή
που θα πέσει η πρώτη αστραπή. Η ΤΜ αυτή (χρόνος) είναι μια αριθμητική αλλά όχι διακριτή
ΤΜ αφού το σύνολο τιμών είναι το διάστημα
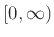 .
.
Παράδειγμα 12.4
Ρίχνουμε ένα νόμισμα (που φέρνει κορώνα με πιθανότητα
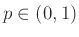 ) άπειρες φορές
και έστω
) άπειρες φορές
και έστω  η πρώτη φορά που έρχεται κορώνα.
Αυτή η ΤΜ έχει το
η πρώτη φορά που έρχεται κορώνα.
Αυτή η ΤΜ έχει το
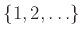 ωσ σύνολο τιμών και είναι άρα διακριτή, αριθμητική ΤΜ.
ωσ σύνολο τιμών και είναι άρα διακριτή, αριθμητική ΤΜ.
Παρατήρηση 12.2
Αν έχουμε μια ΤΜ που παίρνει τιμές σε ένα μη αριθμητικό σύνολο, π.χ. μια ΤΜ που
παίρνει τιμές Κ ή Γ (το αποτέλεσμα της ρίψης ενός νομίσματος), θα κωδικοποιούμε συνήθως
τις τιμές αυτές με φυσικούς αριθμούς, για παράδειγμα 1 αντί Κ και 0 αντί Γ, ώστε να
θεωρούμε ότι οι ΤΜ αυτές παίρνουν αριθμητικές τιμές.
Σε μερικές περιπτώσεις όμως αυτό είναι αρκετά αφύσικο. Για παράδειγμα αν έχουμε μια ΤΜ που παίρνει
ρητές τιμές, μπορούμε φυσικά να κάνουμε αυτή την κωδικοποίηση που σε κάθε ρητό αντιστοιχεί ένα ακέραιο,
όμως αυτή η διαδικασία στερείται φυσικότητας και, κατά κανόνα, δεν πρόκειται να προσφέρει τίποτα
στην ανάλυση.
Πάνω στο δειγματικό χώρο 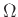 υπάρχει ορισμένη η κατανομή πιθανότητας (δείτε Ορισμό 11.2),
μια συνάρτηση δηλ.
υπάρχει ορισμένη η κατανομή πιθανότητας (δείτε Ορισμό 11.2),
μια συνάρτηση δηλ.
![$ p:\Omega\to[0,1]$](img2175.png) , τ.ώ. η τιμή
, τ.ώ. η τιμή 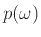 μας δηλώνει πόσο πιθανό
είναι το αποτέλεσμα
μας δηλώνει πόσο πιθανό
είναι το αποτέλεσμα 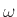 όταν εκτελεσθεί το πείραμα. Αν τώρα
όταν εκτελεσθεί το πείραμα. Αν τώρα
 .
. ένα οποιοδήποτε
σύνολο τιμών) είναι μια ΤΜ
ένα οποιοδήποτε
σύνολο τιμών) είναι μια ΤΜ  με τιμές στο
με τιμές στο 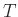 , μπορούμε τότε να θεωρήσουμε ένα νέο
πείραμα με αποτέλεσμα
, μπορούμε τότε να θεωρήσουμε ένα νέο
πείραμα με αποτέλεσμα 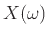 . Εκτελούμε δηλ. το προηγούμενο πείραμα (αυτό με δειγματικό χώρο
. Εκτελούμε δηλ. το προηγούμενο πείραμα (αυτό με δειγματικό χώρο 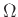 ),
μας δίνει αυτό κάποιο αποτέλεσμα
),
μας δίνει αυτό κάποιο αποτέλεσμα
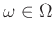 ,
και αναφέρουμε ως αποτέλεσμα του νέου μας πειράματος το
,
και αναφέρουμε ως αποτέλεσμα του νέου μας πειράματος το
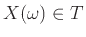 .
Το νέο αυτό πείραμα έχει το
.
Το νέο αυτό πείραμα έχει το 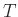 ως δειγματικό χώρο και μια νέα κατανομή πιθανότητας
ως δειγματικό χώρο και μια νέα κατανομή πιθανότητας
![$ p:T \to [0,1]$](img2450.png) που ορίζεται από
που ορίζεται από
Οι πιθανοθεωρητικές ερωτήσεις λοιπόν που αφορούν την ΤΜ  λοιπόν μπορούν να μελετηθούν
πάνω σε αυτόν τον νεό δειγματικό χώρο
λοιπόν μπορούν να μελετηθούν
πάνω σε αυτόν τον νεό δειγματικό χώρο 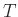 , σύνολο τιμών της
, σύνολο τιμών της  .
Έχει επικρατήσει όμως συχνά να μην αναφερόμαστε στο νέο αυτό δειγματικό χώρο και
να μελετάμε τέτοια ερωτήματα πάνω στον παλιό δειγματικό χώρο
.
Έχει επικρατήσει όμως συχνά να μην αναφερόμαστε στο νέο αυτό δειγματικό χώρο και
να μελετάμε τέτοια ερωτήματα πάνω στον παλιό δειγματικό χώρο 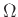 .
Ο κυριότερος λόγος γι' αυτό είναι ότι πολύ συχνά μελετάμε παραπάνω από μια ΤΜ και μάλιστα
σε συνδυασμό, οπότε αν περιοριστεί κανείς στο δειγματικό χώρο
.
Ο κυριότερος λόγος γι' αυτό είναι ότι πολύ συχνά μελετάμε παραπάνω από μια ΤΜ και μάλιστα
σε συνδυασμό, οπότε αν περιοριστεί κανείς στο δειγματικό χώρο 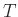 για μια από τις
ΤΜ αυτές, πράξη που πάντα συνεπάγεται «χάσιμο πληροφορίας», δε μπορεί να μελετήσει τις άλλες.
για μια από τις
ΤΜ αυτές, πράξη που πάντα συνεπάγεται «χάσιμο πληροφορίας», δε μπορεί να μελετήσει τις άλλες.
Παρατήρηση 12.4
Η συνάρτηση κατανομής της  ορίζεται για κάθε πραγματικό
ορίζεται για κάθε πραγματικό 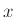 ακόμα κι αν είναι γνωστό εκ
των προτέρων ότι η
ακόμα κι αν είναι γνωστό εκ
των προτέρων ότι η  παίρνει μόνο ακέραιες τιμές. Σε αυτή βέβαια την περίπτωση ισχύει
παίρνει μόνο ακέραιες τιμές. Σε αυτή βέβαια την περίπτωση ισχύει
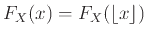 οπότε αρκεί να μελετήσει κανείς την
οπότε αρκεί να μελετήσει κανείς την 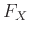 για ακέραιες μόνο τιμές της μεταβλητής.
για ακέραιες μόνο τιμές της μεταβλητής.
Ορισμός 12.3
(Ισόνομες τυχαίες μεταβλητές)
Δύο ΤΜ  και
και 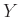 λέγονται ισόνομες αν έχουν την ίδια συνάρτηση κατανομής.
λέγονται ισόνομες αν έχουν την ίδια συνάρτηση κατανομής.
Παρατήρηση 12.5
Δύο ΤΜ  και
και 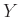 είναι ίσες αν και μόνο αν
είναι ίσες αν και μόνο αν
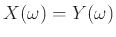 για κάθε
για κάθε
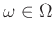 .
Δηλ. για κάθε έκβαση του πειράματος οι
.
Δηλ. για κάθε έκβαση του πειράματος οι  και
και 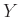 έχουν την ίδια τιμή.
Αυτή είναι πολύ ισχυρή έννοια.
Αντίθετα, δύο ΤΜ είναι ισόνομες αν έχουν απλά (αν πρόκειται για διακριτές μεταβλητές) την ίδια πυκνότητα.
Για παράδειγμα, αν κρατάμε δύο ίδια ζάρια στα χέρια μας και ονομάσουμε
έχουν την ίδια τιμή.
Αυτή είναι πολύ ισχυρή έννοια.
Αντίθετα, δύο ΤΜ είναι ισόνομες αν έχουν απλά (αν πρόκειται για διακριτές μεταβλητές) την ίδια πυκνότητα.
Για παράδειγμα, αν κρατάμε δύο ίδια ζάρια στα χέρια μας και ονομάσουμε  το αποτέλεσμα του πρώτου
και
το αποτέλεσμα του πρώτου
και 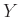 του δεύτερου, τότε οι
του δεύτερου, τότε οι  και
και 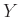 είναι φυσικά ισόνομες αλλά δεν είναι ίσες αφού σε κάποια πειράματα
θα εμφανίσουν διαφορετικές τιμές.
είναι φυσικά ισόνομες αλλά δεν είναι ίσες αφού σε κάποια πειράματα
θα εμφανίσουν διαφορετικές τιμές.
Παράδειγμα 12.5
Αν
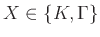 είναι το αποτέλεσμα της ρίψης ενός ζαριού που φέρνει κορώνα
με πιθανότητα
είναι το αποτέλεσμα της ρίψης ενός ζαριού που φέρνει κορώνα
με πιθανότητα
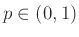 τότε η πυκνότητα πιθανότητας της
τότε η πυκνότητα πιθανότητας της  είναι η συνάρτηση
είναι η συνάρτηση
![$ f_X:{\left\{{K, \Gamma}\right\}} \to [0,1]$](img2466.png) που δίνεται από τις τιμές
που δίνεται από τις τιμές
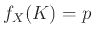 ,
,
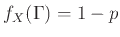 .
.
Παράδειγμα 12.8
Αν 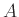 είναι ένα οποιοδήποτε ενδεχόμενο η ΤΜ
είναι ένα οποιοδήποτε ενδεχόμενο η ΤΜ
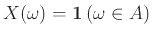 ονομάζεται δείκτρια ΤΜ
του ενδεχομένου
ονομάζεται δείκτρια ΤΜ
του ενδεχομένου 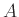 και παίρνει τιμή 1 αν ισχύει το
και παίρνει τιμή 1 αν ισχύει το 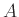 , 0 αλλιώς. Η πυκνότητα πιθανότητας
της
, 0 αλλιώς. Η πυκνότητα πιθανότητας
της 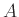 παίρνει την τιμή
παίρνει την τιμή
![$ {{\bf {Pr}}\left[{A}\right]}$](img2194.png) στον αριθμό 1,
στον αριθμό 1,
![$ 1-{{\bf {Pr}}\left[{A}\right]}$](img2484.png) στον αριθμό 0, και 0 παντού αλλού.
στον αριθμό 0, και 0 παντού αλλού.
Άσκηση 12.1
Η συνάρτηση
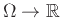 που είναι ίση με
που είναι ίση με 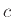 παντού ονομάζεται σταθερή ΤΜ με τιμή
παντού ονομάζεται σταθερή ΤΜ με τιμή 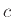 .
Ποια η πυκνότητα πιθανότητάς της και ποια η συνάρτηση κατανομής της;
.
Ποια η πυκνότητα πιθανότητάς της και ποια η συνάρτηση κατανομής της;
Παράδειγμα 12.9
Λέμε ότι η ΤΜ  είναι ομοιόμορφα κατανεμημένη στο (πεπερασμένο) σύνολο
είναι ομοιόμορφα κατανεμημένη στο (πεπερασμένο) σύνολο 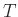 αν η ποσότητα
αν η ποσότητα
![$ {{\bf {Pr}}\left[{X = t}\right]}$](img2486.png) δεν εξαρτάται από το
δεν εξαρτάται από το 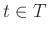 .
Αυτό σημαίνει ότι η πυκνότητα πιθανότητας είναι ίση με
.
Αυτό σημαίνει ότι η πυκνότητα πιθανότητας είναι ίση με
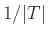 σε κάθε στοιχείο του
σε κάθε στοιχείο του 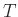 .
.
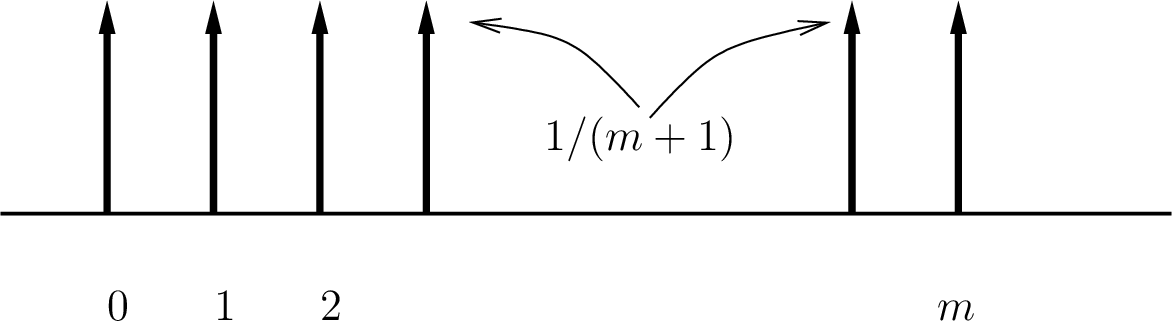
Άσκηση 12.2
Αν  είναι ομοιόμορφα κατανεμημένη στο
είναι ομοιόμορφα κατανεμημένη στο ![$ [n]$](img665.png) και
και 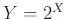 περιγράψτε τις
συναρτήσεις
περιγράψτε τις
συναρτήσεις 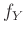 και
και 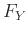 .
.
Άσκηση 12.3
Η ΤΜ
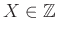 έχει πυκνότητα πιθανότητας
έχει πυκνότητα πιθανότητας 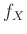 .
Γράψτε από ένα άθροισμα τιμών της
.
Γράψτε από ένα άθροισμα τιμών της 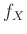 που να δίνει την πιθανότητα των παρακάτω ενδεχομένων:
που να δίνει την πιθανότητα των παρακάτω ενδεχομένων:
-
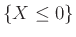
-

-
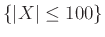 .
.
Άσκηση 12.4
Αν
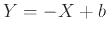 .
.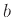 σταθερά, δώστε ένα τύπο για τις
σταθερά, δώστε ένα τύπο για τις 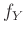 .
.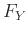 , μέσω των
, μέσω των 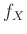 .
.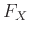 .
.
Παράδειγμα 12.10
Ένα νόμισμα φέρνει κορώνα με πιθανότητα
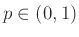 .
Το ρίχνουμε άπειρες φορές και έστω
.
Το ρίχνουμε άπειρες φορές και έστω  η ρίψη κατά την οποία εμφανίζεται η πρώτη κορώνα.
Είναι φανερό ότι
η ρίψη κατά την οποία εμφανίζεται η πρώτη κορώνα.
Είναι φανερό ότι
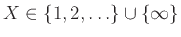 , αφού μπορεί κατά τη διάρκει του πειράματος
να μην εμφανιστεί ποτέ κορώνα.
(Το ότι χρησιμοποιήσαμε το σύμβολο
, αφού μπορεί κατά τη διάρκει του πειράματος
να μην εμφανιστεί ποτέ κορώνα.
(Το ότι χρησιμοποιήσαμε το σύμβολο 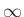 για να δηλώσουμε ότι δεν έρχεται ποτέ κορώνα
κατά κάποια εκτέλεση του πειράματος πρόκειται απλά για μια σύμβαση και δεν έχει τίποτε να κάνει
με τις ιδιότητες μεγέθους που δίδει κανείς συνήθως στο σύμβολο
για να δηλώσουμε ότι δεν έρχεται ποτέ κορώνα
κατά κάποια εκτέλεση του πειράματος πρόκειται απλά για μια σύμβαση και δεν έχει τίποτε να κάνει
με τις ιδιότητες μεγέθους που δίδει κανείς συνήθως στο σύμβολο 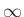 , π.χ. ότι είναι
μεγαλύτερο από κάθε φυσικό αριθμό.
Θα μπορούσαμε δηλ. εξίσου καλά να δίδαμε τιμή
, π.χ. ότι είναι
μεγαλύτερο από κάθε φυσικό αριθμό.
Θα μπορούσαμε δηλ. εξίσου καλά να δίδαμε τιμή 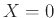 ή
ή 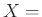 «ΠΟΤΕ» στην περίπτωση αυτή.)
Ας είναι
«ΠΟΤΕ» στην περίπτωση αυτή.)
Ας είναι 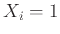 αν το νόμισμα φέρει κορώνα στην
αν το νόμισμα φέρει κορώνα στην 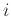 -οστή ρίψη και
-οστή ρίψη και 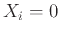 αν φέρει γράμματα.
Έχουμε, για
αν φέρει γράμματα.
Έχουμε, για
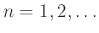 ,
,
και, λόγω της ανεξαρτησίας των ενδεχομένων
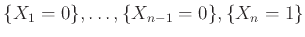 ,
,
![$\displaystyle f_X(n) = {{\bf {Pr}}\left[{X_1=0}\right]} \cdots {{\bf {Pr}}\left[{X_{n-1} = 0}\right]} \cdot {{\bf {Pr}}\left[{X_n = 1}\right]} = p (1-p)^{n-1},$](img2505.png) |
(12.2) |
και για κάθε 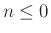 έχουμε προφανώς
έχουμε προφανώς
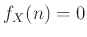 .
Τέλος επειδή
.
Τέλος επειδή
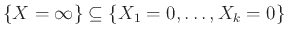 για κάθε
για κάθε 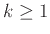 , και επειδή η πιθανότητα
του δεύτερου ενδεχομένου ισούται με
, και επειδή η πιθανότητα
του δεύτερου ενδεχομένου ισούται με 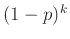 , και άρα συγκλίνει στο 0 με το
, και άρα συγκλίνει στο 0 με το  , έπεται ότι
, έπεται ότι
Έχουμε λοιπόν προσδιορίσει πλήρως την πυκνότητα της  .
.
Η  δεν είναι αριθμητική ΤΜ αφού παίρνει και την τιμή
δεν είναι αριθμητική ΤΜ αφού παίρνει και την τιμή 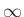 , οπότε
δεν ορίζεται η συνάρτηση κατανομής.
Όμως, μπορεί κανείς να μελετήσει την ΤΜ
, οπότε
δεν ορίζεται η συνάρτηση κατανομής.
Όμως, μπορεί κανείς να μελετήσει την ΤΜ
που είναι σχεδόν σίγουρα ίση με την  (όσον αφορά τις πιθανοθεωρητικές τους ιδιότητες δύο ΤΜ που είναι ίσες σχεδόν σίγουρα
είναι ουσιαστικά η ίδια ΤΜ και τις θεωρούμε μία)
αφού
(όσον αφορά τις πιθανοθεωρητικές τους ιδιότητες δύο ΤΜ που είναι ίσες σχεδόν σίγουρα
είναι ουσιαστικά η ίδια ΤΜ και τις θεωρούμε μία)
αφού
![$ {{\bf {Pr}}\left[{X \neq Y}\right]} = {{\bf {Pr}}\left[{X = \infty}\right]} = 0$](img2511.png) .
Γι' αυτό εφαρμόζουμε τον τύπο (12.1).
Για
.
Γι' αυτό εφαρμόζουμε τον τύπο (12.1).
Για 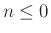 έχουμε φυσικά
έχουμε φυσικά
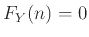 .
Για
.
Για 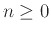 έχουμε
(
έχουμε
(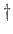 : αλλαγή μεταβλητής
: αλλαγή μεταβλητής 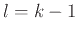 .
.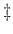 : πεπερασμένη γεωμ. σειρά).
: πεπερασμένη γεωμ. σειρά).
Η πυκνότητα (12.2) ονομάζεται γεωμετρική κατανομή με παράμετρο 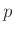 .
.
Άσκηση 12.5
Έχουμε 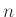 παίκτες που ρίχνουν από ένα τίμιο νόμισμα ο καθένας.
Όσοι από αυτούς φέρουν κορώνα ξαναρίχνουν το νόμισμά τους και έστω
παίκτες που ρίχνουν από ένα τίμιο νόμισμα ο καθένας.
Όσοι από αυτούς φέρουν κορώνα ξαναρίχνουν το νόμισμά τους και έστω  ο αριθμός αυτών που ξαναφέρνουν κορώνα.
Να βρεθεί η πυκνότητα πιθανότητας της ΤΜ
ο αριθμός αυτών που ξαναφέρνουν κορώνα.
Να βρεθεί η πυκνότητα πιθανότητας της ΤΜ  .
.
Παράδειγμα 12.13
Αν 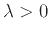 είναι μια παράμετρος, η πυκνότητα
είναι μια παράμετρος, η πυκνότητα
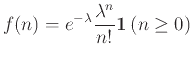 |
(12.4) |
ονομάζεται κατανομή Poisson με παράμετρο 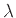 .
Για να επιβεβαιώσουμε ότι η (12.4) είναι όντως μια πυκνότητα
αρκεί να επικαλεστούμε τον τύπο
.
Για να επιβεβαιώσουμε ότι η (12.4) είναι όντως μια πυκνότητα
αρκεί να επικαλεστούμε τον τύπο
που ισχύει για κάθε
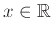 .
.
Άσκηση 12.6
Η  ακολουθεί γεωμετρική κατανομή με παράμετρο
ακολουθεί γεωμετρική κατανομή με παράμετρο 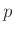 .
Βρείτε την πυκνότητα της
.
Βρείτε την πυκνότητα της 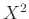 .
.
Άσκηση 12.7
Η  ακολουθεί γεωμετρική κατανομή με παράμετρο
ακολουθεί γεωμετρική κατανομή με παράμετρο 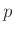 και
και 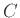 είναι σταθερά.
Ορίζουμε
είναι σταθερά.
Ορίζουμε
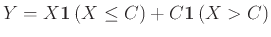 .
Να βρεθεί η πυκνότητα της
.
Να βρεθεί η πυκνότητα της 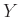 .
.
Ορισμός 12.4
Έστω
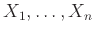 διακριτές ΤΜ πάνω σε ένα δειγματικό χώρο
διακριτές ΤΜ πάνω σε ένα δειγματικό χώρο 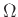 .
Αυτές λέγονται ανεξάρτητες ΤΜ αν για κάθε
.
Αυτές λέγονται ανεξάρτητες ΤΜ αν για κάθε
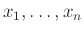 ισχύει
ισχύει
Ένα άπειρο σύνολο από ΤΜ πάνω στον ίδιο δειγματικό χώρο λέγεται ανεξάρτητο
αν κάθε πεπερασμένο υποσύνολο είναι ανεξάρτητο.
Άσκηση 12.8
Δείξτε ότι αν οι διακριτές ΤΜ  και
και 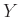 είναι ανεξάρτητες τότε για οποιαδήποτε σύνολα
είναι ανεξάρτητες τότε για οποιαδήποτε σύνολα 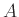 και
και 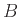 ισχύει
ισχύει
![$ {{\bf {Pr}}\left[{X \in A, Y \in B}\right]} = {{\bf {Pr}}\left[{X \in A}\right]} {{\bf {Pr}}\left[{Y \in B}\right]}$](img2558.png) .
.
Άσκηση 12.9
Δείξτε ότι αν οι  και
και 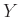 είναι ανεξάρτητες τότε και οι
είναι ανεξάρτητες τότε και οι 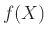 .
.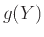 είναι ανεξάρτητες,
όπου
είναι ανεξάρτητες,
όπου 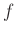 και
και 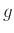 είναι τυχούσες συναρτήσεις.
είναι τυχούσες συναρτήσεις.
Άσκηση 12.10
Οι  και
και 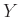 είναι ανεξάρτητες και ισόνομες και
είναι ανεξάρτητες και ισόνομες και
![$ {{\bf {Pr}}\left[{X=1}\right]}={{\bf {Pr}}\left[{X=-1}\right]}=1/2$](img2560.png) .
Ορίζουμε
.
Ορίζουμε 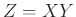 .
Δείξτε ότι οι
.
Δείξτε ότι οι 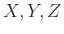 είναι ανεξάρτητες ανά δύο αλλά όχι ανεξάρτητες.
είναι ανεξάρτητες ανά δύο αλλά όχι ανεξάρτητες.
Άσκηση 12.11
Οι  και
και 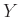 είναι ανεξάρτητες και ισόνομες και
είναι ανεξάρτητες και ισόνομες και
![$ {{\bf {Pr}}\left[{X=k}\right]} = 2^{-k}$](img2562.png) ,
,
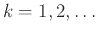 .
Υπολογίστε τις ποσότητες
.
Υπολογίστε τις ποσότητες
-
![$ {{\bf {Pr}}\left[{\min{\left\{{X,Y}\right\}} \le n}\right]}$](img2564.png) ,
,
-
![$ {{\bf {Pr}}\left[{Y>X}\right]}$](img2565.png) ,
,
-
![$ {{\bf {Pr}}\left[{X=Y}\right]}$](img2566.png) ,
,
-
![$ {{\bf {Pr}}\left[{X \ge kY}\right]}$](img2567.png) , για δοσμένο θετικό ακέραιο
, για δοσμένο θετικό ακέραιο  ,
,
-
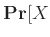 διαιρεί
διαιρεί ![$ Y]$](img2569.png) ,
,
-
![$ {{\bf {Pr}}\left[{X=rY}\right]}$](img2570.png) , για δοσμένο θετικό ρητό
, για δοσμένο θετικό ρητό 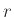 .
.
Ορισμός 12.5
(Συνέλιξη)
Έστω
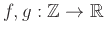 συναρτήσεις που ικανοποιούν
συναρτήσεις που ικανοποιούν
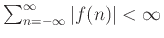 και ομοίως για την
και ομοίως για την 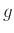 .
Η συνάρτηση
.
Η συνάρτηση 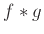 που ορίζεται στην Άσκηση 12.12
ονομάζεται συνέλιξη των
που ορίζεται στην Άσκηση 12.12
ονομάζεται συνέλιξη των 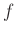 και
και 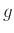 .
.
Άσκηση 12.13
Δείξτε ότι 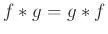 και
και
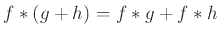 , όταν όλες οι συνελίξεις ορίζονται.
, όταν όλες οι συνελίξεις ορίζονται.
Παρατήρηση 12.7
Χρησιμοποιώντας την Άσκηση 12.12 βλέπουμε ότι
αν 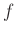 και
και 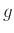 είναι πυκνότητες πιθανότητας, αν δηλ. υπάρχουν ΤΜ
είναι πυκνότητες πιθανότητας, αν δηλ. υπάρχουν ΤΜ  και
και 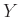 τέτοιες ώστε
τέτοιες ώστε
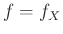 και
και 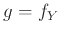 , ή, ισοδύναμα, αν
για κάθε μια από τις
, ή, ισοδύναμα, αν
για κάθε μια από τις 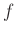 και
και 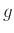 ισχύουν τα
ισχύουν τα
-
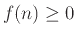 , για κάθε
, για κάθε
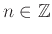 ,
,
-
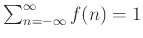 ,
,
τότε και η συνέλιξη 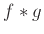 επίσης είναι πυκνότητα πιθανότητας.
επίσης είναι πυκνότητα πιθανότητας.
Θεώρημα 12.1
Αν  και
και 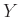 είναι ανεξάρτητες ΤΜ με ακέραιες τιμές τότε
είναι ανεξάρτητες ΤΜ με ακέραιες τιμές τότε
για κάθε
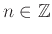 .
.
Απόδειξη.
(
: από Θεώρημα
11.3).

Άσκηση 12.14
Να βρεθεί η 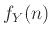 μέσω της
μέσω της 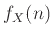 αν
αν 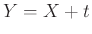 , όπου
, όπου 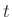 ένας σταθερός ακέραιος.
ένας σταθερός ακέραιος.
Mihalis Kolountzakis
2015-11-28
![]() και το σύνολο τιμών
και το σύνολο τιμών ![]() είναι πεπερασμένο ή αριθμήσιμο τότε η ΤΜ
είναι πεπερασμένο ή αριθμήσιμο τότε η ΤΜ ![]() ονομάζεται διακριτή.
ονομάζεται διακριτή.![]() αν υπάρχει επί συνάρτηση
αν υπάρχει επί συνάρτηση
![]() από το σύνολο
των φυσικών αριθμών επί του
από το σύνολο
των φυσικών αριθμών επί του ![]() .
Με άλλα λόγια, το
.
Με άλλα λόγια, το ![]() είναι αριθμήσιμο αν μπορούμε να βρούμε μια ακολουθία
είναι αριθμήσιμο αν μπορούμε να βρούμε μια ακολουθία
![]() που περιέχει όλα τα στοιχεία του.
που περιέχει όλα τα στοιχεία του.
![]() , οι ακέραιοι
, οι ακέραιοι
![]() , οι ρητοί
, οι ρητοί
![]() ,
καρτεσιανά γινόμενα
,
καρτεσιανά γινόμενα
![]() , όπου τα
, όπου τα ![]() και
και ![]() είναι αριθμήσιμα, και άπειρες ενώσεις
του τύπου
είναι αριθμήσιμα, και άπειρες ενώσεις
του τύπου
![]() , όπου τα
, όπου τα ![]() είναι αριθμήσιμα.
είναι αριθμήσιμα.
![]() ή ένα διάστημα
ή ένα διάστημα ![]() .
.![]() .
Αυτό το τελευταίο δεν είναι προφανές και θέλει απόδειξη, την οποία δε θα δώσουμε εδώ.
.
Αυτό το τελευταίο δεν είναι προφανές και θέλει απόδειξη, την οποία δε θα δώσουμε εδώ.
![]() ,
,
![]() , είναι ΤΜ τέτοιες ώστε η
, είναι ΤΜ τέτοιες ώστε η ![]() έχει σύνολο τιμών
το
έχει σύνολο τιμών
το
![]() , τότε η ΤΜ
, τότε η ΤΜ
![]() ορίζεται χωρίς πρόβλημα
αφού η σειρά πάντα συγκλίνει, ότι τιμές και να έχουν τα
ορίζεται χωρίς πρόβλημα
αφού η σειρά πάντα συγκλίνει, ότι τιμές και να έχουν τα ![]() , αλλά μπορεί εν δυνάμει (για παράδειγμα
όταν όλες οι
, αλλά μπορεί εν δυνάμει (για παράδειγμα
όταν όλες οι ![]() είναι ανεξάρτητες - δείτε παρακάτω τον Ορισμό 12.4
για τον ορισμό της ανεξαρτησίας ΤΜ) να πάρει
οποιονδήποτε πραγματικό αριθμό του διαστήματος
είναι ανεξάρτητες - δείτε παρακάτω τον Ορισμό 12.4
για τον ορισμό της ανεξαρτησίας ΤΜ) να πάρει
οποιονδήποτε πραγματικό αριθμό του διαστήματος ![]() ως τιμή. Πράγματι, αν
ως τιμή. Πράγματι, αν
![]() τότε,
γράφοντας τον
τότε,
γράφοντας τον ![]() στο δυαδικό του ανάπτυγμα
στο δυαδικό του ανάπτυγμα
![]() , με
, με
![]() ,
βλέπουμε ότι είναι δυνατό να έχουμε
,
βλέπουμε ότι είναι δυνατό να έχουμε ![]() φτάνει να πάρουν οι
φτάνει να πάρουν οι ![]() τις κατάλληλες τιμές.
τις κατάλληλες τιμές.![]() υπάρχει ορισμένη η κατανομή πιθανότητας (δείτε Ορισμό 11.2),
μια συνάρτηση δηλ.
υπάρχει ορισμένη η κατανομή πιθανότητας (δείτε Ορισμό 11.2),
μια συνάρτηση δηλ.
![]() , τ.ώ. η τιμή
, τ.ώ. η τιμή ![]() μας δηλώνει πόσο πιθανό
είναι το αποτέλεσμα
μας δηλώνει πόσο πιθανό
είναι το αποτέλεσμα ![]() όταν εκτελεσθεί το πείραμα. Αν τώρα
όταν εκτελεσθεί το πείραμα. Αν τώρα
![]() .
.![]() ένα οποιοδήποτε
σύνολο τιμών) είναι μια ΤΜ
ένα οποιοδήποτε
σύνολο τιμών) είναι μια ΤΜ ![]() με τιμές στο
με τιμές στο ![]() , μπορούμε τότε να θεωρήσουμε ένα νέο
πείραμα με αποτέλεσμα
, μπορούμε τότε να θεωρήσουμε ένα νέο
πείραμα με αποτέλεσμα ![]() . Εκτελούμε δηλ. το προηγούμενο πείραμα (αυτό με δειγματικό χώρο
. Εκτελούμε δηλ. το προηγούμενο πείραμα (αυτό με δειγματικό χώρο ![]() ),
μας δίνει αυτό κάποιο αποτέλεσμα
),
μας δίνει αυτό κάποιο αποτέλεσμα
![]() ,
και αναφέρουμε ως αποτέλεσμα του νέου μας πειράματος το
,
και αναφέρουμε ως αποτέλεσμα του νέου μας πειράματος το
![]() .
Το νέο αυτό πείραμα έχει το
.
Το νέο αυτό πείραμα έχει το ![]() ως δειγματικό χώρο και μια νέα κατανομή πιθανότητας
ως δειγματικό χώρο και μια νέα κατανομή πιθανότητας
![]() που ορίζεται από
που ορίζεται από
![]() με τιμές στο
με τιμές στο
![]() ορίζουμε τη συνάρτηση κατανομής
της
ορίζουμε τη συνάρτηση κατανομής
της ![]() ως τη συνάρτηση
ως τη συνάρτηση
![]() που δίδεται από τον τύπο
που δίδεται από τον τύπο
![]() τότε για κάθε
τότε για κάθε
![]() έχουμε
έχουμε
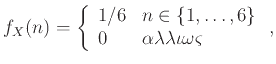
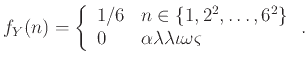
![]() δεν είναι αριθμητική ΤΜ αφού παίρνει και την τιμή
δεν είναι αριθμητική ΤΜ αφού παίρνει και την τιμή ![]() , οπότε
δεν ορίζεται η συνάρτηση κατανομής.
Όμως, μπορεί κανείς να μελετήσει την ΤΜ
, οπότε
δεν ορίζεται η συνάρτηση κατανομής.
Όμως, μπορεί κανείς να μελετήσει την ΤΜ
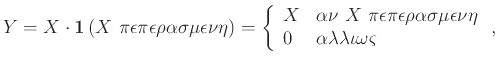
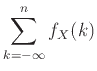
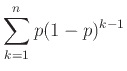
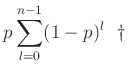
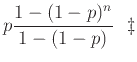
![]() .
.
![]() δεν είναι διακριτή, οπότε δεν ορίζουμε συνάρτηση πυκνότητας πιθανότητας.
Όμως η συνάρτηση κατανομής της
δεν είναι διακριτή, οπότε δεν ορίζουμε συνάρτηση πυκνότητας πιθανότητας.
Όμως η συνάρτηση κατανομής της ![]() ορίζεται και είναι πολύ εύκολο να υπολογιστεί, αφού λόγω της ομοιόμορφης
κατανομής έχουμε
ορίζεται και είναι πολύ εύκολο να υπολογιστεί, αφού λόγω της ομοιόμορφης
κατανομής έχουμε
![]() . Αν λοιπόν
. Αν λοιπόν ![]() τότε
τότε
![]() , αν
, αν ![]() τότε
τότε
![]() και αν
και αν
![]() τότε
τότε
![]() .
.
![]() και
και ![]() .
.
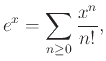
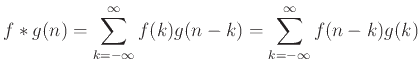
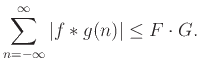
![]() ή
ή ![]() , αφού οι
, αφού οι ![]() και
και ![]() είναι ισόνομες (έχουν δηλ. την ίδια κατανομή).
Το ότι η
είναι ισόνομες (έχουν δηλ. την ίδια κατανομή).
Το ότι η ![]() είναι ομοιόμορφα κατανεμημένη στο
είναι ομοιόμορφα κατανεμημένη στο
![]() σημαίνει ακριβώς ότι
σημαίνει ακριβώς ότι