1.9 Μαθηματική Επαγωγή

1.9.1 Η μέθοδος στην απλή της μορφή

Η μέθοδος της μαθηματικής επαγωγής χρησιμοποιείται για να αποδείξουμε προτάσεις οι οποίες εξαρτώνται, στην απλούστερη περίπτωση, από μια ακέραια μεταβλητή, η οποία συνήθως, αλλά όχι πάντα, συμβολίζεται με το γράμμα $n$. Συμβολίζουμε συνήθως με $P(n)$ την πρόταση αυτή. Έτσι, $P(0)$ σημαίνει ότι η πρόταση είναι αληθής για $n=0$, $P(1)$ ότι είναι αληθής για $n=1$, κ.ο.κ. Σκοπός μας είναι να δείξουμε την αλήθεια της $P(n)$, για $n\ge n_0$, όπου $n_0$ είναι ένας ακέραιος, συνήθως μη αρνητικός, αριθμός. Θέλουμε με άλλα λόγια να δείξουμε την αλήθεια των προτάσεων

$$P(n_0), P(n_0+1), P(n_0+2), \ldots.$$

Η μέθοδος, λοιπόν, της επαγωγής για την απόδειξη της πρότασης

$$\forall n\ge n_0: P(n),$$ (1.9)

συνίσταται στην απόδειξη των εξής δύο προτάσεων:

$$P(n_0)$$ (1.10)

και

$$\forall n\ge n_0: P(n) \Rightarrow P(n+1) .$$ (1.11)

Για να δείξουμε δηλ. ότι ισχύει η πρόταση για όλες τις τιμές του $n$ που θέλουμε, δηλ. για $n\ge n_0$, δείχνουμε πρώτα ότι ισχύει για $n=n_0$ και επίσης δείχνουμε ότι αν ισχύει για μια τιμή του $n$ τότε ισχύει και για την επόμενη, δηλ. για το $n+1$. Η (1.10) ονομάζεται αρχική ή βασική περίπτωση και η (1.11) ονομάζεται επαγωγικό βήμα. Η υπόθεση $P(n)$ στο επαγωγικό βήμα ονομάζεται επαγωγική υπόθεση.

Παράδειγμα 1.22   Να δειχτεί ότι, για $n\ge 1$,

$$1+2+\cdots+n = {1 \over 2}n(n+1).$$ (1.12)

Εδώ η αρχική τιμή της παραμέτρου $n$ είναι $n=1$, οπότε ελέγχουμε πρώτα απ' όλα αν ισχύει η πρόταση για $n=1$. Προφανώς το αρισερό μέλος ισούται με $1$ ενώ, αντικαθιστώντας, βλέπουμε ότι το ίδιο ισχύει και για το δεξί. Άρα ισχύει η βασική περίπτωση και προχωρούμε να δείξουμε το επαγωγικό βήμα.

Η επαγωγική υπόθεση είναι τώρα η (1.12) (με την υπόθεση πάντα ότι $n\ge 1$) και πρέπει χρησιμοποιώντας την να δείξουμε την ίδια πρόταση όπου το $n$ έχει αντικατασταθεί με $n+1$, την ισότητα δηλαδή

$$1+2+\cdots+n+(n+1) = {1\over 2}(n+1)(n+2).$$ (1.13)

Όμως, χρησιμοποιώντας την (1.12) (αφαιρώντας την (1.12) από την (1.13) κατά μέλη) η (1.13) είναι ισοδύναμη με την ισότητα

$$n+1 = {1\over 2}(n+1)(n+2) - {1 \over 2}n(n+1)$$

που εύκολα ελέγχουμε με απλές πράξεις ότι ισχύει. Δείξαμε λοιπόν και το επαγωγικό βήμα οπότε η επαγωγική απόδειξη είναι πλήρης.

Παρατήρηση 1.2   Είναι σημαντικό να τονίσουμε ότι για να μπορεί να χρησιμοποιηθεί η μέθοδος της επαγωγής πρέπει η παράμετρος της πρότασης ($n$ στο προηγούμενο παράδειγμα) απαραίτητα να παίρνει τιμές σε ένα σύνολο (στο προηγούμενο παράδειγμα ήταν οι φυσικοί αριθμοί) που να μπορεί να εξαντληθεί αν ξεκινήσουμε από τη βασική περίπτωση και προχωράμε κάθε φορά κατά ένα.

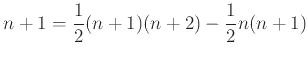
Έτσι δε μπορεί να χρησιμοποιηθεί η μέθοδος της επαγωγής όταν π.χ. η παράμετρος μπορεί να πάρει οποιαδήποτε πραγματική τιμή.

Ας δούμε, για παράδειγμα, την πρόταση

$P(x):$ ο πραγματικός αριθμός $x$ είναι ακέραιος.

Το $P(0)$ προφανώς ισχύει και το ίδιο ισχύει και η συνεπαγωγή $P(x) \Rightarrow P(x+1)$, δεν ισχύει όμως η πρόταση για όλες τις (πραγματικές) τιμές της παραμέτρου $x$, αλλά μόνο για όσες είναι προσιτές από το βασικό αριθμό 0 με διαδοχικές αυξήσεις κατά 1, είναι δηλ. αληθής για τους φυσικούς αριθμούς αλλά όχι για όλους τους πραγματικούς.

Άσκηση 1.14   Δείξτε επαγωγικά ότι για $n\ge 1$ ισχύει

$$1^2+2^2+\cdots+n^2 = {1\over6}n(n+1)(2n+1).$$ (1.14)

Παράδειγμα 1.23   Να δειχτεί ότι $2^n > n^3$ για $n \ge 10$.

Για την αρχική τιμή $n=10$ πρέπει να δείξουμε

$$2^{10} = 1024 > 10^3 = 1000,$$

που ισχύει.

Για το επαγωγικό βήμα υποθέτουμε ότι $n \ge 10$ και ότι $2^n > n^3$ και πρέπει να δείξουμε ότι $2^{n+1} > (n+1)^3$.

Πολλαπλασιάζοντας την επαγωγική μας υπόθεση με 2 παίρνουμε $2^{n+1} > 2n^3$. Αρκεί λοιπόν να δείξουμε ότι, για $n \ge 10$, ισχύει $2n^3 \ge (n+1)^3$. Αυτή γράφεται ισοδύναμα ως

$$(2^{1/3} n)^3 \ge (n+1)^3,$$

ή

$$2^{1/3} n \ge n+1,$$

ή

$$n \ge {1 \over 2^{1/3}-1},$$

που ισχύει για $n \ge 10$ αφού ισχύει για $n=10$ (απλές πράξεις).

Άσκηση 1.15   Ας δείξουμε επαγωγικά την εξής πρόταση: για κάθε σύνολο από $n$ άλογα ($n\ge 1$) όλα έχουν το ίδιο χρώμα. Για $n=1$ άλογο η πρόταση είναι προφανώς αληθινή. Ας δείξουμε και το επαγωγικό βήμα. Υποθέτουμε ότι ισχύει η πρόταση για $n$ άλογα και τη δείχνουμε για $n+1$. Έστω λοιπόν άλογα $a_1, a_2, \ldots, a_n, a_{n+1}$. Από την επαγωγική υπόθεση τα $n$ άλογα $a_1,\ldots,a_n$ έχουν όλα το ίδιο χρώμα. Επίσης από την επαγωγική υπόθεση τα $n$ άλογα $a_2,\ldots,a_{n+1}$ έχουν όλα το ίδιο χρώμα. Άρα έχουν όλα τα άλογα το ίδιο χρώμα. (Δείτε Σχήμα 1.8.)

Σχήμα 1.8: Έχουν όλα τα άλογα το ίδιο χρώμα;

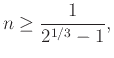
Πού είναι το λάθος;

Άσκηση 1.16   Οι αριθμοί Fibonacci $F_i$.$i\ge 1$, ορίζονται αναδρομικά από

$$F_1 = F_2 = 1, \kappa\alpha\iota F_n = F_{n-1}+F_{n-2} \gamma\iota\alpha n>2.$$

Δείξτε με επαγωγή ότι για $n\ge 1$ ο αριθμός $F_{3n}$ είναι άρτιος.

Άσκηση 1.17   Για την ακολουθία Fibonacci της Άσκησης 1.16 δείξτε ότι ισχύει για $n\ge 1$

$$F_{n+2}^2 - F_{n+1}^2 = F_n F_{n+3}.$$

Σχήμα 1.9: Τέσσερεις ευθείες που ορίζουν 11 χωρία στο επίπεδο

Άσκηση 1.18   Δίνονται $n$ ευθείες στο επίπεδο. Σε πόσα το πολύ χωρία χωρίζουν αυτές το επίπεδο; (Δείτε το Σχήμα 1.9.)

Άσκηση 1.19   Σε μία χώρα κάθε μια από τις $n\ge 2$ πόλεις της συνδέεται με κάθε άλλη με ένα μονόδρομο. Δηλ. αν $A$ και $B$ είναι δύο από τις πόλεις τότε υπάρχει είτε ο δρόμος από το $A$ στο $B$ είτε ο δρόμος από το $B$ στο $A$, αλλά δεν ξέρουμε ποιος. Δείξτε ότι υπάρχει τρόπος να ξεκινήσει κανείς από μία πόλη της χώρας αυτής και να επισκεφτεί κάθε άλλη, ακριβώς μία φορά, κινούμενος πάνω στο υπάρχον οδικό δίκτυο (και σεβόμενος τους μονόδρομους).

Άσκηση 1.20   Δείξτε ότι για κάθε $x \in {\mathbb{R}}\setminus{\left\{{1}\right\}}$ ισχύει ο τύπος για την πεπερασμένη γεωμετρική σειρά

$$1+x+x^2+\cdots+x^n = {1-x^{n+1} \over 1-x}, n\ge1.$$ (1.15)

Από αυτό δείξτε ότι, αν ${\left\vert{x}\right\vert}<1$, τότε για την άπειρη γεωμετρική σειρά ισχύει

$$\sum_{k=0}^\infty x^k = 1+x+x^2+\cdots+x^n+\cdots = {1 \over 1-x}.$$ (1.16)

Άσκηση 1.21   Αν υποθέσαμε ότι δεν γνωρίζατε τον τύπο για την πεπερασμένη γεωμετρική σειρά της Άσκησης 1.20, πώς θα βρίσκατε ένα τύπο για το αριστερό μέλος της (1.15);

Υπόδειξη: Ονομάστε $A$ το αριστερό μέλος της (1.15) και βρείτε μια εξίσωση για το $A$ προσθέτοντας $x^{n+1}$ και στα δύο μέλη και εμφανίζοντας το $A$ και στο αριστερό μέλος.

Άσκηση 1.22   Αποδείξτε ότι για $R>0, n\ge 0$ ισχύει ο τύπος

$$(R (\cos x + i \sin x))^n = R^n (\cos{nx} + i \sin{nx}).$$

Εδώ $i$ είναι ο μιγαδικός αριθμός με την ιδιότητα $i^2 = -1$. Αυτή η ιδιότητα του $i$ αρκεί για να δείξετε το ζητούμενο (θα χρειαστείτε και τους τύπους για $\cos(a+b), \sin(a+b)$ μέσω των τριγωνομετρικών αριθμών των $a, b$).

Άσκηση 1.23   Έστω $n \ge 0$ και ότι έχουμε μια σκακιέρα με $2^n \times 2^n$ τετράγωνα από την οποία κάποιος έχει αφαιρέσει ένα τετράγωνο (την έχει τρυπήσει). Έχουμε επίσης στη διάθεσή μας απεριόριστα «τριόμινα», που είναι ξύλινα κομμάτια από 3 τετράγωνα (ίδια τετράγωνα με της σκακιέρας) σε σχήμα Γ. Αποδείξτε ότι είναι δυνατό να καλύψετε ακριβώς την τρυπημένη σκακιέρα με τριόμινα, χωρίς αυτά να αλληλοεπικαλύπτονται.

Άσκηση 1.24   Αποδείξτε ότι για $n\ge 1$ ο αριθμός $7$ διαιρεί την ποσότητα $2^{n+2}+3^{2n+1}$.

Άσκηση 1.25   Έστω ένα πολυώνυμο $f(x_1, x_2, \ldots, x_n)$ σε $n$ πραγματικές μεταβλητές. Το πολυώνυμο γράφεται ως άθροισμα μονωνύμων με κάποιους συντελεστές και υποθέτουμε ότι δεν είναι όλοι οι συντελεστές 0. Δείξτε ότι το $f$ δεν είναι ταυτοτικα 0, υπάρχουν δηλ. $x_1, x_2, \ldots, x_n \in {\mathbb{R}}^n$ τέτοια ώστε $f(x_1, x_2, \ldots, x_n) \neq 0$.

1.9.1.1 Όλες οι προηγούμενες περιπτώσεις ως επαγωγική υπόθεση

Η μέθοδος της λεγόμενης ισχυρής μαθηματικής επαγωγής αποδεικνύει την αλήθεια μιας πρότασης $P(n)$, για $n\ge n_0$, δείχνοντας κατ' αρχήν την αλήθεια της πρότασης $P(n_0)$ (σε αυτό ταυτίζεται με τη συνηθισμένη επαγωγή) αλλά το επαγωγικό βήμα συνίσταται στην απόδειξη της συνεπαγωγής

$$P(n_0), P(n_0+1), \ldots, P(n-1), P(n) \Rightarrow P(n+1).$$

Με άλλα λόγια, για να δείξουμε την πρόταση $P(n+1)$ μας επιτρέπεται να χρησιμοποιήσουμε την αλήθεια όλων των προηγουμένων περιπτώσεων, και όχι μόνο της αμέσως προηγούμενης.

Παράδειγμα 1.24   Πρώτος λέγεται ένας φυσικός αριθμός μεγαλύτερος του 1 αν οι μόνοι διαιρέτες του είναι το 1 και ο εαυτός του. Δείχνουμε ότι κάθε φυσικός αριθμός $n\ge 2$ είναι γινόμενο πρώτων αριθμών (ισχύει και μοναδικότητα του αναπτύγματος αυτού αλλά δεν το αποδεικνύουμε αυτό εδώ).

Η βασική περίπτωση είναι η $n=2$. Αφού το 2 είναι πρώτος αριθμός η πρόταση ισχύει. Έστω τώρα $n>2$ και ας υποθέσουμε ότι η πρόταση ισχύει για όλες τις μικρότερες τιμές. Υποθέτουμε δηλ. ότι αν $2\le k < n$ τότε ο φυσικός αριθμός $k$ μπορεί να γραφεί σα γινόμενο πρώτων αριθμών. Οφείλουμε να δείξουμε, χρησιμοποιώντας αυτή την υπόθεση, οτι και ο $n$ γράφεται σα γινόμενο πρώτων.

Αν ο $n$ είναι πρώτος αριθμός τότε ισχύει φυσικά αυτό. Άρα μπορούμε να υποθέσουμε οτι ο $n$ δεν είναι πρώτος. Αυτό σημαίνει ότι υπάρχει κάποιος φυσικός αριθμός $k$, διαφορετικός από το 1 και από το $n$, που διαιρεί το $n$. Αυτό συνεπάγεται ότι $1<k<n$, άρα, σύμφωνα με την επαγωγική υπόθεση, οι αριθμοί $k$ και $n/k$ (για τον οποίο επίσης ισχύει $1<n/k<n$) γράφονται σα γινόμενο πρώτων. Το ίδιο ισχύει συνεπώς και για τον $n$ που ισούται με το γινόμενό τους.

Άσκηση 1.26   Δείξτε ότι κάθε φυσικός αριθμός $n \ge 0$ μπορεί να γραφτεί στη μορφή

$$n = n_k 2^k + n_{k-1} 2^{k-1} + \cdots + n_1 2 + n_0$$

για κάποιο φυσικό $k \ge 1$ και αριθμούς $n_0, n_1, \ldots, n_k \in {\left\{{0, 1}\right\}}$. (Αυτό ονομάζεται δυαδικό ανάπτυγμα του $n$ και μπορείτε εύκολα να δείξετε ότι είναι μοναδικό.)

Άσκηση 1.27   Κάθε ακέραια αξία $n \ge 12$ μπορεί να φτιαχτεί με κέρματα αξίας 4 και 5.

Άσκηση 1.28   Η ακολουθία $a_n$.$n\ge 1$, ορίζεται από τους τύπους

$$a_1 = 1, a_2 = 3, a_n = a_{n-1}+a_{n-2} (n\ge 3).$$

Δείξτε ότι $a_n < (7/4)^n$, για $n\ge 1$.

Άσκηση 1.29   Η ακολουθία $a_n$.$n\ge 1$, ορίζεται από τους τύπους

$$a_1 = 1, a_2 = 1, a_n = a_{n-1}+a_{n-2} (n\ge 3).$$

Δείξτε ότι για $n\ge 1$ έχουμε $a_n = \frac{a^n-b^n}{a-b}$ όπου $a=(1+\sqrt{5})/2, b=(1-\sqrt{5})/2$

1.9.2 Προχωρημένη χρήση της επαγωγής

1.9.2.1 «Μπρος-πίσω» επαγωγή

Μερικές φορές η μέθοδος επαγωγής για την απόδειξης μιας πρότασης $P(n)$ μπορεί να τροποποιηθεί ώστε αντί για να αποδεικνύουμε το επαγωγικό βήμα $P(n) \Rightarrow P(n+1)$, πράγμα που μπορεί να είναι δύσκολο να γίνει, αποδεικνύουμε ότι η πρόταση $P(n)$ συνεπάγεται το $P(k)$ για κάποιο $k$ πολύ μεγαλύτερο του $n+1$, αλλά ταυτόχρονα αποδεικνύουμε και ότι $P(n+1) \Rightarrow P(n)$. Μαζί αυτές οι δύο συνεπαγωγές συνεπάγονται την αλήθεια της πρότασης για όλα τα $n$, αφού η προς τα εμπρός συνεπαγωγή μας επιτρέπει να αποδείξουμε την ισχύ της πρότασης για μια άπειρη ακολουθία από τιμές του $n$ ενώ με τη δεύτερη συνεπαγωγή «γυρίζουμε προς τα πίσω και γεμίζουμε τα κενά».

Παράδειγμα 1.25   Ας αποδείξουμε την ανισότητα γεωμετρικού-αριθμητικού μέσου: αν $n\ge 1$ και $a_1, a_2, \ldots, a_n \ge 0$ τότε

$$(a_1 \cdot a_2 \cdots a_n)^{1/n} \le \frac{a_1 + a_2 + \cdots + a_n}{n}.$$ (1.17)

Το αριστερό μέλος της (1.17) λέγεται γεωμετρικός μέσος των αριθμών $a_1, a_2, \ldots, a_n$ ενώ το δεξί μέλος είναι ο αριθμητικός τους μέσος.

Κατ' αρχήν αποδεικνύουμε την πρόταση για $n=2$ οπότε και γίνεται

$$(a_1 a_2)^{1/2} \le \frac{a_1 + a_2}{2},$$

η οποία, μετά από λίγες πράξεις, ανάγεται στην ανισότητα $(a_1 - a_2)^2 \ge 0$ που προφανώς ισχύει.

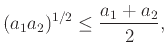
Δείχνουμε έπειτα ότι αν η (1.17) ισχύει για το $n$ τότε ισχύει και για το $2n$. Πράγματι αν $a_1, a_2, \ldots, a_{2n} \ge 0$ και θέσουμε

$$A=\frac{1}{n}(a_1+\cdots+a_n), a=(a_1 \cdot a_2 \cdots a_n)^{1/n},$$

$$B=\frac{1}{n}(a_{n+1}+\cdots+a_{2n}), b=(a_{n+1}\cdots a_{2n})^{1/n}$$

τότε από την περίπτωση $2$ και την περίπτωση $n$ έχουμε

$$\frac{a_1+\cdots+a_{2n}}{2n} =\frac{A+B}{2} \dagger$$

$$\ge \frac{a+b}{2} \ddagger$$

$$\ge (ab)^{1/2} *$$

$$= (a_1\cdots a_{2n})^{1/(2n)} \dagger$$

($\dagger$: πράξεις, $\ddagger$: περίπτωση $n$.$*$: περίπτωση 2).

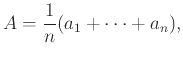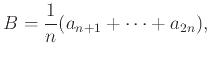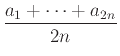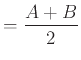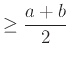Μέχρι στιγμής λοιπόν έχουμε δείξει ότι η πρόταση ισχύει για όλα τα $n$ που είναι δυνάμεις του 2. Το επόμενο βήμα είναι να αποδείξουμε ότι αν ισχύει η πρόταση για το $n$ τότε ισχύει και για το $n-1$, και αυτό συμπληρώνει την απόδειξη για όλα τα $n$.

Ας υποθέσουμε λοιπόν ότι ισχύει η ανισότητα (1.17) για κάποιο $n$ και ας είναι $a_1,\ldots,a_{n-1} \ge 0$ κάποιοι μη αρνητικοί αριθμοί. Επιλέγουμε $a_n = C := \frac{a_1+\cdots + a_{n-1}}{n-1}$, αντικαθιστούμε στην (1.17), λύνουμε ως προς $C$ και προκύπτει το ζητούμενο (εύκολες πράξεις).

1.9.2.2 Πολλαπλή επαγωγή

Πολλές φορές η πρόταση που θέλουμε να δείξουμε εξαρτάται από περισσότερες από μία παραμέτρους. Μπορεί, για παράδειγμα, να προκειται για μια πρόταση $P(m,n)$ που εξαρτάται από δύο παραμέτρους $m,n\ge 0$. Η μέθοδος της επαγωγής μπορεί μερικές φορές να εφαρμοστεί και σε τέτοιες περιπτώσεις. Στην απλούστερη περίπτωση το πρόβλημα αντιμετωπίζεται σα μια επαλληλία μονοπαραμετρικών προβλημάτων.

Σε μια τυπική τέτοια περίπτωση αποδεικνύεται πρώτα η πρόταση $P(0,0)$, και μετά δείχνουμε τη συνεπαγωγή

$$P(m,n) \Rightarrow P(m+1,n).$$ (1.18)

Με μόνα αυτά τα δύο βήματα στο «οπλοστάσιό» μας δε μπορούμε ακόμη να ξεφύγουμε από τη γραμμή $n=0$. Αν όμως αποδείξουμε και τη συνεπαγωγή

$$\left( \forall m\ge0 \forall k<n P(m, k) \right) \Rightarrow P(0,n),$$ (1.19)

τότε έχουμε μια πλήρη απόδειξη για όλα τα ζεύγη των τιμών $(m,n)$.

Σχήμα 1.10: Διπλή επαγωγή

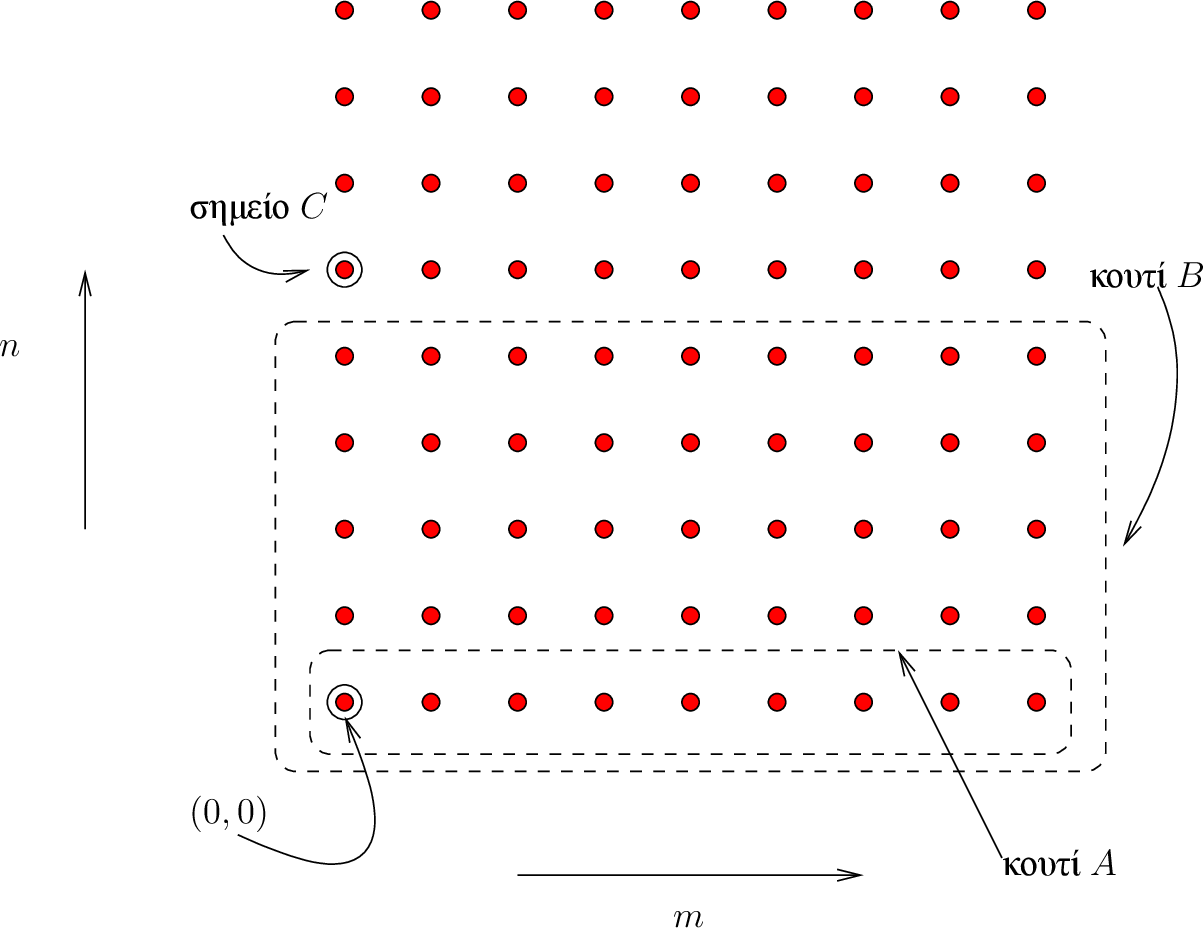
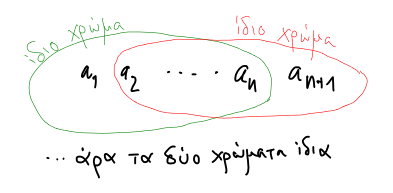
Ας περιγράψουμε λίγο το τι σημαίνουν αυτές οι συνεπαγωγές που μοιάζουν (και είναι) αρκετά αυθαίρετες. Αυτό που θέλουμε είναι να αποδείξουμε την αλήθεια της πρότασης $P(m,n)$ σε όλα τα ακέραια σημεία του τεταρτημορίου $m,n\ge 0$ του επιπέδου. Ας αναφερθούμε στο Σχήμα 1.10 όπου παριστάνεται σχηματικά το τεταρτημόριο αυτό.

Με το βασικό βήμα της επαγωγής αποδεικνύουμε την αλήθεια της $P(\cdot,\cdot)$ στο σημείο $(0,0)$. Μετά την απόδειξη της (1.18) μπορούμε επεκτείνουμε την αλήθεια της $P(\cdot,\cdot)$ σε όλο το (ημιάπειρο) «κουτί $A$», που αποτελείται από όλα τα σημεία του τύπου $(\cdot,0)$. Και αυτό γιατί το νόημα της συνεπαγωγής (1.18) είναι ότι η αλήθεια της πρότασης επεκτείνεται από κάθε σημείο στο αμέσως δεξιά του.

Για να επεκτείνουμε την αλήθεια της $P(\cdot,\cdot)$ και προς τα πάνω χρειάζεται να έχουμε και ένα «κανόνα» που να συνάγει την αλήθεια της $P(\cdot,\cdot)$ σε ένα σημείο γνωρίζοντας την αλήθεια αυτής σε σημεία που είναι αυστηρά χαμηλότερα. Αυτός είναι ακριβώς ο ρόλος της συνεπαγωγής (1.19). Αν, για παράδειγμα, γνωρίζουμε ότι η $P$ αληθεύει στο «κουτί $B$», δηλ. σε όλα τα σημεία του τύπου $(m,k)$, όπου το $m$ είναι οτιδήποτε και $k<n$, συμπεραίνουμε τότε ότι η $P(0,n)$ (στο «σημείο $C$») ισχύει. Με σημείο αφετηρίας τώρα το σημείο $C$ και χρησιμοποιώντας ξανά τη συνεπαγωγή 1.18 επεκτείνουμε την αλήθεια της $P$ στη γραμμή ακριβώς πάνω από το κουτί $B$. Συνεχίζοντας με αυτό τον τρόπο επ' άπειρον βλέπουμε ότι η πρόταση αληθεύει παντού στο τεταρτημόριο που μας ενδιαφέρει.

Πρέπει να τονίσουμε εδώ ότι υπάρχουν πολλοί τρόποι να γίνει η επαγωγή σε παραπάνω από μία μεταβλητή, και ότι αυτός που αναφέραμε παραπάνω είναι απλά ένας από αυτούς. Αυτό που χρειάζεται σε μια εφαρμογή της επαγωγής είναι ένα επαγωγικό βήμα που να μπορεί να «καλύψει» όλο το σύνολο των τιμών που παίρνουν οι παράμετροι ($m$ και $n$ στον τρόπο που περιγράψαμε παραπάνω) ξεκινώντας από μερικές απλές βασικές περιπτώσεις. Ιδού ένα άλλο παράδειγμα: ας υποθέσουμε ότι οι παράμετροι $m$ και $n$ της πρότασής μας παίρνουν όλες τους φυσικούς αριθμούς ως τιμές και ότι μπορούμε εύκολα να αποδείξουμε την πρότασή μας αν $m=0$ ή αν $n=0$ (συνοριακές συνθήκες). Επίσης, για κάθε ζεύγος τιμών $m$ και $n$ όπου και τα δύο είναι τουλάχιστον 1, η αλήθεια της πρότασης προκύπτει από την αλήθεια της πρότασης στα σημεία $(m-1,n-1)$ και $(m-1,n)$ (τα σημεία ακριβώς αριστερά και αριστερά-κάτω από το $(m,n)$ στο Σχήμα 1.10). Τότε η πρόταση αληθεύει για όλα τα $m,n\ge 0$ αφού για οποιοδήποτε τέτοιο ζεύγος μπορεί κανείς με διαδοχικές αναγωγές να οδηγηθεί να εξαρτάται από την αλήθεια της πρότασης στο σύνορο του τεταρτημορίου, όπου γνωρίζουμε ότι αυτή ισχύει. Δείτε και την Άσκηση 1.30.

Άσκηση 1.30   Η ακολουθία $a(n,k)$ ορίζεται για $n,k \ge 0$, και ικανοποιεί τα παρακάτω.

$$a(n,0) = 1, (n\ge0),$$

$$a(n,k) = 0, (n<k),$$

και

$$a(n,k) = a(n-1,k-1) + a(n-1,k), (n\ge k \ge 1).$$

Δείξτε ότι για $n\ge k \ge 1$ ισχύει

$$a(n,k) = {n(n-1)(n-2)\cdots(n-k+1) \over 1\cdot2\cdot3\cdots k}.$$

1.9.2.3 Ενισχύοντας την πρόταση που θέλουμε να δείξουμε

Πολλές φορές, και παρ' ότι εκ πρώτης όψεως μπορεί να φαίνεται παράδοξο, όταν πάμε να δείξουμε με επαγωγή μια πρόταση $P$ είναι ευκολότερο να δείξουμε μια ισχυρότερη πρόταση $Q$, μια πρόταση δηλ. για την οποία να ισχύει για κάθε $n$ η συνεπαγωγή $Q(n) \Rightarrow P(n)$.

Αυτό δεν είναι και τόσο περίεργο αν σκεφτούμε ότι στο επαγωγικό βήμα (1.11) η πρόταση $P$ εμφανίζεται στο συμπέρασμα αλλά και στην υπόθεση. Δηλ. ναι μεν δυσκολεύουμε κάπως τη ζωή μας (περνώντας από την $P$ στην $Q$) αφού έχουμε να αποδείξουμε κάτι δυσκολότερο από πριν, ενισχύουμε όμως ταυτόχρονα και την επαγωγική μας υπόθεση οπότε δεν είναι προφανές ότι χάνουμε. Σε πολλές περιπτωσεις κερδίζουμε στην ευκολία απόδειξης.

Παράδειγμα 1.26   Να δειχτεί ότι ο αριθμός $1+3+5+\cdots+2n-1$ (άθροισμα των πρώτων $n$ περιττών φυσικών αριθμών) είναι τέλειο τετράγωνο για $n\ge 1$.

Ας γράψουμε για απλότητα $S_n = 1 + 3 + \cdots + 2n-1$, οπότε $S_{n+1} = S_n + 2n+1$. Για $n=1$ προφανώς ισχύει η πρόταση αφού $S_1 = 1 = 1^2$.

Για το επαγωγικό βήμα υποθέτουμε ότι ισχύει $S_n = t^2$ για κάποιο ακέραιο $t$. Έχουμε τότε

$$S_{n+1} = S_n + 2n+1 = t^2 + 2n +1.$$

Δυστυχώς από δω και πέρα δεν υπάρχει τρόπος να δείξουμε ότι η ποσότητα $t^2 + 2n +1$ είναι τέλειο τετράγωνο.

Αν όμως αντί να δείξουμε την πρόταση

$P(n): S_n$ είναι τέλειο τετράγωνο,

δείξουμε την ισχυρότερη πρόταση

$$Q(n): S_n = n^2,$$

η οποία προφανώς συνεπάγεται την $P(n)$, τότε μας λύνονται τα χέρια, αφού παραπάνω από την επαγωγική υπόθεση $t=n$ και σε αυτή την περίπτωση η ποσότητα $t^2 + 2n +1$ είναι ίση με $(n+1)^2$, και έχουμε λοιπόν δείξει το επαγωγικό βήμα.

Άσκηση 1.31 (Ανισότητα Bernoulli)   Δείξτε με επαγωγή ως προς $n$ ότι για κάθε φυσικό αριθμό $n \ge 0$ και πραγματικό αριθμό $x\ge -1$ ισχύει

$$(1+x)^n \ge 1+nx.$$ (1.20)

Δοκιμάστε τώρα να δείξετε με επαγωγή την ασθενέστερη ανισότητα $(1+x)^n \ge nx$.

1.9.3 Εφαρμογή: Το θεώρημα του Γάμου (Hall)

Έστω $X$ ένα, πεπερασμένο ή άπειρο, σύνολο και $A_1,\ldots,A_n \subseteq X$ ένα σύστημα υποσυνόλων του $X$. Για απλότητα μπορούμε να θεωρήσουμε ότι το σύνολο $X$ είναι πεπερασμένο, αν και όλες οι αποδείξεις ισχύουν και για άπειρο $X$ (αλλά πάντα τα $A_i$ πρέπει να είναι πεπερασμένα).

Ορισμός 1.23   (Σύστημα Ξένων Αντιπροσώπων) Τα στοιχεία $x_1 \in A_1, \ldots, x_n \in A_n$ ονομάζονται ένα Σύστημα Ξένων Αντιπροσώπων (ΣΞΑ) για το σύστημα συνόλων $A_1,\ldots,A_n$ αν τα $x_1,\ldots,x_n$ είναι όλα διαφορετικά.

Το πρόβλημα που θα μας απασχολήσει είναι να βρούμε συνθήκες για την ύπαρξη ενός ΣΞΑ για ένα σύστημα συνόλων

$${\mathcal{F}} = {\left\{{A_1,\ldots,A_n}\right\}}.$$

Η ονομασία «θεώρημα του Γάμου» προέρχεται από την εξής αναλογία: υποθέτουμε ότι έχουμε $n$ γυναίκες $\Gamma_1,\ldots,\Gamma_n$ και ότι $A_i$ είναι το σύνολο των ανδρών που αποδέχεται η γυναίκα $\Gamma_i$ ως συζύγους. (Δείτε το Σχήμα 1.11.) Το ερώτημα είναι πότε μπορούμε να διαλέξουμε από ένα σύζυγο για κάθε γυναίκα, από αυτούς που αποδέχεται, και διαφορετικό για κάθε γυναίκα. Αυτό λοιπόν γίνεται αν και μόνο αν η οικογένεια υποσυνόλων $A_1,\ldots,A_n$ (του συνόλου όλων των ανδρών) έχει κάποιο σύστημα ξένων αντιπροσώπων.

Σχήμα 1.11: Πώς ορίζονται τα σύνολα $A_i$ και $A(J)$

Ορισμός 1.24   Για κάθε $J \subseteq [n] := {\left\{{1, 2, \ldots, n}\right\}}$ ορίζουμε

$$A(J) = A_{\mathcal{F}}(J) = \bigcup_{j\in J} A_j.$$

Ο δείκτης ${\mathcal{F}}$ θα παραλείπεται όταν δεν υπάρχει πρόβλημα σύγχυσης.

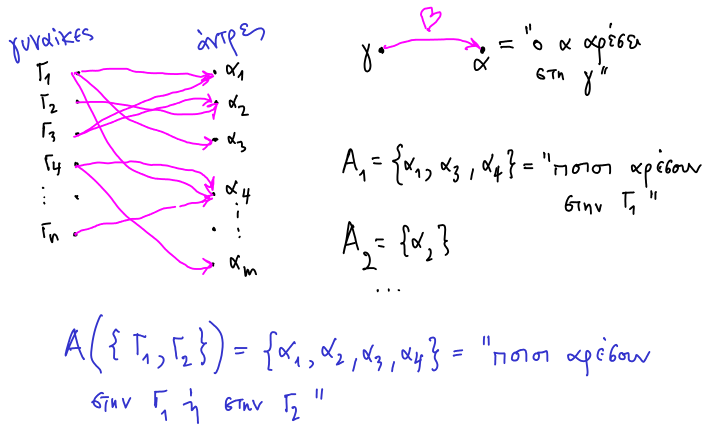
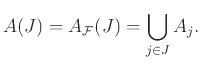
Είναι φανερό πως αν το σύστημα ${\mathcal{F}}$ έχει ένα ΣΞΑ ${\left\{{x_1,\ldots,x_n}\right\}}$ τότε έχουμε

$$\forall J \subseteq [n]: {\left\vert{A(J)}\right\vert} \ge {\left\vert{J}\right\vert}.$$ (1.21)

Αυτό γιατί το σύνολο $A(J)$ περιέχει τουλάχιστον τα $x_j, j\in J$, τα οποία εξ ορισμού είναι όλα διαφορετικά.

Η συνθήκη (1.21) λέγεται συνθήκη του Hall και το επόμενο θεώρημα μας λέει ότι εκτός από αναγκαία είναι και ικανή για την ύπαρξη ενός ΣΞΑ για το σύστημα συνόλων ${\mathcal{F}}$.

Θεώρημα 1.5   (Το θεώρημα του Γάμου)
Το σύστημα συνόλων ${\mathcal{F}}$ έχει ΣΞΑ αν και μόνο αν ισχύει η συνθήκη του Hall (1.21).

Απόδειξη. Επαγωγή ως πρός $n$. Για $n=1$ το θεώρημα είναι προφανές. Υποθέτουμε πως ισχύει μέχρι και $n-1$. Εστω ${\mathcal{F}}={\left\{{A_1,\ldots,A_n}\right\}}$ ένα σύστημα υποσυνόλων του $X$ που ικανοποιεί την (1.21). Ενα σύνολο $J\subset [n]$, $J\neq \emptyset,[n]$, λέγεται κρίσιμο αν ${\left\vert{A(J)}\right\vert} = {\left\vert{J}\right\vert}$.

Περίπτωση 1η: Δεν υπάρχει κρίσιμο σύνολο $J$.
Από την (1.21) το $A_1$ έχει τουλάχιστον ένα στοιχείο, έστω $x_1$. Θεωρούμε τώρα το σύστημα υποσυνόλων του $X\setminus{\left\{{x_1}\right\}}$

$${\mathcal{F}}' = {\left\{{A_2',\ldots,A_n'}\right\}},$$

με $A_j' = A_j \setminus {\left\{{x_1}\right\}}$, $j=2,\ldots,n$. Εστω $J \subseteq {\left\{{2,\ldots,n}\right\}}$. Αφού το $J$ δεν είναι κρίσιμο για το σύστημα ${\mathcal{F}}$ έχουμε

$${\left\vert{A_{\mathcal{F}'}(J)}\right\vert} \ge {\left\vert{A_{\mathcal{F}}(J)}\right\vert} - 1$$

$$> {\left\vert{J}\right\vert} -1$$

$$\ge {\left\vert{J}\right\vert},$$

άρα η συνθήκη του Hall (1.21) ισχύει για το σύστημα ${\mathcal{F}}'$. Από την επαγωγική υπόθεση υπάρχει ένα ΣΞΑ $x_2,\ldots,x_n$ για το ${\mathcal{F}}'$. Είναι εύκολο τότε να δεί κανείς πως τα $x_1,x_2,\ldots,x_n$ είναι ένα ΣΞΑ για το ${\mathcal{F}}$.

Περίπτωση 2η: Υπάρχει κάποιο κρίσιμο σύνολο.
Εστω $J$ ένα κρίσιμο σύνολο με το ελάχιστο δυνατό μέγεθος. Για απλούστευση μπορούμε να θεωρήσουμε ότι $J={\left\{{1,\ldots,k}\right\}}$. Εχουμε τότε ${\left\vert{A(J)}\right\vert} = {\left\vert{J}\right\vert}$. Αφού η συνθήκη του Hall ισχύει για το σύστημα ${\mathcal{F}}$ είναι φανερό ότι θα ισχύει και για το σύστημα $A_1,\ldots,A_k$ υποσυνόλων του $A(J)$. Αφού $k<n$ συμπεραίνουμε από την επαγωγική υπόθεση πως υπάρχει ΣΞΑ $x_1,\ldots,x_k \in A(J)$ για τα $A_1,\ldots,A_k$.

Θα δείξουμε ότι υπάρχει και ένα ΣΞΑ για τα σύνολα $A_{k+1},\ldots,A_n$ με όλους τους αντιπροσώπους $\notin A(J)$, και έτσι θα έχει ολοκληρωθεί η απόδειξη. Γι'αυτό θα δείξουμε ότι ισχύει η συνθήκη του Hall για το σύστημα ${\mathcal{F}}' = {\left\{{A_{k+1}',\ldots,A_n'}\right\}}$ υποσυνόλων του $X \setminus A(J)$, με

$$A_j' = A_j \setminus A(J), j=k+1,\ldots,n.$$

Εστω λοιπόν $I \subseteq {\left\{{k+1,\ldots,n}\right\}}$. Πρέπει να δείξουμε ${\left\vert{A_{{\mathcal{F}}'}(I)}\right\vert} \ge {\left\vert{I}\right\vert}$.

Από τη συνθήκη του Hall για το αρχικό σύστημα ${\mathcal{F}}$ έχουμε

$${\left\vert{A_{\mathcal{F}}(I \cup J)}\right\vert} \ge {\left\ver... ...\cup J}\right\vert} = {\left\vert{I}\right\vert} + {\left\vert{J}\right\vert}.$$

Αλλά είναι φανερό ότι επίσης έχουμε

$$A_{\mathcal{F}}(I \cup J) = A_{{\mathcal{F}}'}(I) \cup A_{\mathcal{F}}(J),$$

όπου η ένωση είναι ξένη.

Επεται ότι

$${\left\vert{A_{{\mathcal{F}}'}(I)}\right\vert} = {\left\vert{A_{\mathcal{F}}(I \cup J)}\right\vert} - {\left\vert{A_{\mathcal{F}}(J)}\right\vert}$$

$$= {\left\vert{A_{\mathcal{F}}(I \cup J)}\right\vert} - {\left\vert{J}\right\vert}$$

$$\ge {\left\vert{I \cup J}\right\vert} - {\left\vert{J}\right\vert}$$

$$= {\left\vert{I}\right\vert} + {\left\vert{J}\right\vert} - {\left\vert{J}\right\vert}$$

$$= {\left\vert{I}\right\vert},$$

που είναι αυτό που θέλαμε να δείξουμε. Αρα το σύστημα ${\mathcal{F}}'$ έχει ΣΞΑ του οποίου η ένωση με το ΣΞΑ ${\left\{{x_1,\ldots,x_k}\right\}}$ του συστήματος $A_1,\ldots,A_k$, μας δίνει ένα ΣΞΑ για το αρχικό σύστημα ${\mathcal{F}}$. $\qedsymbol$