12.2 Μέση τιμή μιας ΤΜ
Ορισμός 12.6
(Μέση τιμή μιας τυχαίας μεταβλητής)
Αν  είναι μια ΤΜ με ακέραιες τιμές τότε ορίζουμε τη μέση τιμή της
είναι μια ΤΜ με ακέραιες τιμές τότε ορίζουμε τη μέση τιμή της  μέσω του τύπου
μέσω του τύπου
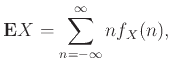 |
(12.5) |
αν η σειρά συγκλίνει απόλυτα, αν έχουμε δηλαδή
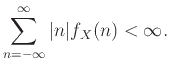 |
(12.6) |
Γενικότερα, αν
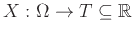 είναι οποιαδήποτε διακριτή ΤΜ, με
είναι οποιαδήποτε διακριτή ΤΜ, με 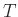 αριθμήσιμο,
τότε η μέση τιμής της ορίζεται από τον τύπο
αριθμήσιμο,
τότε η μέση τιμής της ορίζεται από τον τύπο
![$\displaystyle {\bf E}{X} = \sum_{t \in T} t\cdot {{\bf {Pr}}\left[{X = t}\right]},$](img2619.png) |
(12.7) |
και πάλι μόνο όταν
![$\displaystyle \sum_{t \in T} {\left\vert{t}\right\vert}\cdot {{\bf {Pr}}\left[{X = t}\right]}<\infty,$](img2620.png) |
(12.8) |
Παρατήρηση:
Η μέση τιμή μιας ΤΜ  , αν υπάρχει, είναι ένας κυρτός συνδυασμός
των τιμών της
, αν υπάρχει, είναι ένας κυρτός συνδυασμός
των τιμών της  . Κυρτός συνδυασμός κάποιων αριθμών (ή διανυσμάτων)
. Κυρτός συνδυασμός κάποιων αριθμών (ή διανυσμάτων)
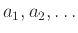 είναι μια ποσότητα της μορφής
είναι μια ποσότητα της μορφής
όπου
![$ \lambda_j \in [0,1]$](img2629.png) για κάθε
για κάθε 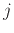 και
και
Η διαφορά δηλ. από το συνηθισμένο γραμμικό συνδυασμό είναι ο περιορισμός
στους συντελεστές ότι πρέπει να είναι μη αρνητικοί και το άθροισμά τους πρέπει να κάνει 1.
Αφού λοιπόν
![$ {\bf E}{X} = \sum_{j \in {\mathbb{Z}}} j {{\bf {Pr}}\left[{X=j}\right]}$](img2631.png) και οι συντελεστές μπροστά από
τις δυνατές τιμες
και οι συντελεστές μπροστά από
τις δυνατές τιμες 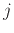 της ακέραιας ΤΜ
της ακέραιας ΤΜ  , δηλ. οι ποσότητες
, δηλ. οι ποσότητες
![$ {{\bf {Pr}}\left[{X=j}\right]}$](img2632.png) , είναι μη αρνητικοί
και έχουν άθροισμα 1, έπεται ότι όντως η μέση τιμή της
, είναι μη αρνητικοί
και έχουν άθροισμα 1, έπεται ότι όντως η μέση τιμή της  είναι κυρτός συνδυασμός των δυνατών
τιμών της
είναι κυρτός συνδυασμός των δυνατών
τιμών της  (όλων των ακεραίων δηλ.).
(όλων των ακεραίων δηλ.).
Άσκηση 12.16
Αν
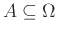 είναι ένα ενδεχόμενο και
είναι ένα ενδεχόμενο και
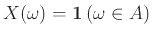 υπολογίστε
τη
υπολογίστε
τη
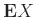 .
.
Άσκηση 12.17
Αν η  ακολουθεί κατανομή Poisson (δείτε (12.4))
με παράμετρο
ακολουθεί κατανομή Poisson (δείτε (12.4))
με παράμετρο 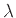 δείξτε ότι
δείξτε ότι
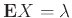 .
.
Άσκηση 12.18
Δείξτε ότι αν η σταθερά 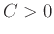 οριστεί κατάλληλα τότε η συνάρτηση
οριστεί κατάλληλα τότε η συνάρτηση
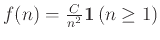 είναι πυκνότητα πιθανότητας και ότι
οποιαδήποτε ΤΜ με πυκνότητα
είναι πυκνότητα πιθανότητας και ότι
οποιαδήποτε ΤΜ με πυκνότητα
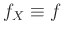 δεν έχει μέση τιμή
δεν έχει μέση τιμή
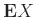 .
.
Παράδειγμα 12.15
Αν
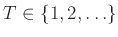 είναι ο χρόνος εμφάνισης της πρώτης κορώνας
σε μια άπειρη ακολουθία ρίψεως ενός νομίσματος που έρχεται κορώνα με πιθανότητα
είναι ο χρόνος εμφάνισης της πρώτης κορώνας
σε μια άπειρη ακολουθία ρίψεως ενός νομίσματος που έρχεται κορώνα με πιθανότητα 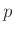 ,
η πυκνότητα της
,
η πυκνότητα της 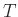 δίνεται από τον τύπο
δίνεται από τον τύπο
οπότε
Πραγωγίζοντας τη σειρά
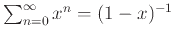 κατά όρους παίρνουμε
κατά όρους παίρνουμε
Εφαρμόζοντας αυτό τον τύπο για 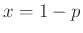 παίρνουμε
παίρνουμε
Ο μέσος χρόνος εμφάνισης δηλ. της πρώτης κορώνας είναι αντιστρόφως ανάλογος της πιθανότητας εμφάνισης
κορώνας σε μια ρίψη του νομίσματος.
Η πιο σημαντική ιδιότητα της μέσης τιμής είναι η γραμμικότητά της.
Είναι σκόπιμο να τονιστεί εδώ πως, αντίθετα με το Θεώρημα 12.4 παρακάτω,
το Θεώρημα 12.2 δεν απαιτεί ανεξαρτησία των ΤΜ. Εκεί έγκειται και η μεγάλη χρησιμότητά του.
Θεώρημα 12.2
Αν οι διακριτές ΤΜ  και
και 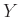 έχουν μέση τιμή και
έχουν μέση τιμή και
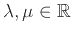 είναι σταθερές, τότε
η ΤΜ
είναι σταθερές, τότε
η ΤΜ
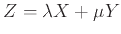 έχει μέση τιμή και
έχει μέση τιμή και
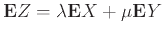 .
.
Απόδειξη.
Έστω
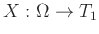
και
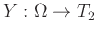
, όπου τα σύνολα
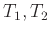
είναι αριθμήσιμα.
Ορίζουμε τα ενδεχόμενα
και
Έχουμε
και
οπότε
αφού τα ενδεχόμενα
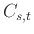
,
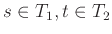
, αποτελούν διαμέριση του
στα οποία η ΤΜ
είναι σταθερή (δείτε Παρατήρηση
12.8).

Παράδειγμα 12.16
Στο Παράδειγμα 12.14 μπορούμε να υπολογίσουμε τη
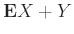 χωρίς να χρησιμοποιήσουμε καθόλου τη συνάρτηση πυκνότητας της
χωρίς να χρησιμοποιήσουμε καθόλου τη συνάρτηση πυκνότητας της 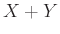 που υπολογίσαμε εκεί.
Για την
που υπολογίσαμε εκεί.
Για την  έχουμε από την Άσκηση 12.19 ότι
έχουμε από την Άσκηση 12.19 ότι
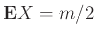 αφού η ομοιόμορφη κατανομή στο
αφού η ομοιόμορφη κατανομή στο
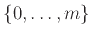 είναι συμμετρική γύρω από το σημείο
είναι συμμετρική γύρω από το σημείο 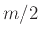 .
Τέλος
.
Τέλος
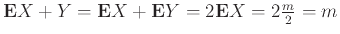 .
.
Παράδειγμα 12.18
Σ' ένα δωμάτιο μπαίνουν 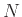 άτομα και αφήνουν τα καπέλα τους στον προθάλαμο, όπου όμως
παίζουν κάποια παιδιά και ανακατεύουν τα καπέλα. Φεύγοντας τα
άτομα και αφήνουν τα καπέλα τους στον προθάλαμο, όπου όμως
παίζουν κάποια παιδιά και ανακατεύουν τα καπέλα. Φεύγοντας τα 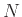 άτομα παίρνουν από ένα καπέλο
στην τύχη. Ποιος είναι ο μέσος αριθμός των ατόμων που παίρνουν το δικό τους καπέλο;
άτομα παίρνουν από ένα καπέλο
στην τύχη. Ποιος είναι ο μέσος αριθμός των ατόμων που παίρνουν το δικό τους καπέλο;
Η ΤΜ που μας ενδιαφέρει είναι η  , ο αριθμός των ατόμων, που παίρνουν το δικό τους καπέλο.
Ας είναι
, ο αριθμός των ατόμων, που παίρνουν το δικό τους καπέλο.
Ας είναι 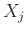 ,
,
 , οι ΤΜ
, οι ΤΜ
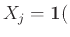 το άτομο
το άτομο 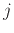 παίρνει το δικό του καπέλο).
(Οι ΤΜ
παίρνει το δικό του καπέλο).
(Οι ΤΜ 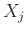 δεν είναι ανεξάρτητες. Γιατί;)
Είναι φανερό ότι
δεν είναι ανεξάρτητες. Γιατί;)
Είναι φανερό ότι
Άρα, από το Θεώρημα 12.2 έχουμε
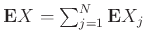 .
Επίσης, λόγω της συμμετρίας, έχουμε ότι οι
.
Επίσης, λόγω της συμμετρίας, έχουμε ότι οι 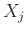 είναι ισόνομες, άρα
είναι ισόνομες, άρα
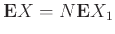 .
Τέλος
.
Τέλος
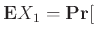 ο 1 παίρνει το καπέλο του
ο 1 παίρνει το καπέλο του ![$ ] = 1/n$](img2681.png) , επίσης λόγω της συμμετρίας.
Άρα
, επίσης λόγω της συμμετρίας.
Άρα
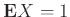 .
Είναι εντυπωσιακό ότι το
.
Είναι εντυπωσιακό ότι το
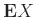 δεν εξαρτάται από το
δεν εξαρτάται από το 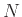 .
.
Το «σπάσιμο» της ΤΜ  σαν άθροισμα άλλων απλουστέρων, και μάλιστα δεικτριών, ΤΜ είναι ένα
πολύ χρήσιμο εργαλείο στη λύση προβλημάτων.
σαν άθροισμα άλλων απλουστέρων, και μάλιστα δεικτριών, ΤΜ είναι ένα
πολύ χρήσιμο εργαλείο στη λύση προβλημάτων.
Το παρακάτω είναι εξαιρετικά χρήσιμο σε υπολογισμούς.
Θεώρημα 12.3
Αν  είναι μια διακριτή ΤΜ (όχι αναγκαστικά αριθμητική) και
είναι μια διακριτή ΤΜ (όχι αναγκαστικά αριθμητική) και 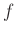 μια αριθμητική συνάρτηση ορισμένη στο πεδίο
τιμών
μια αριθμητική συνάρτηση ορισμένη στο πεδίο
τιμών 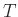 της
της  τότε η ΤΜ
τότε η ΤΜ 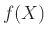 έχει μέση τιμή αν
έχει μέση τιμή αν
και αυτή τότε ισούται με
Απόδειξη.
Η απόδειξη είναι άμεση αν εφαρμόσουμε την Παρατήρηση
12.8 στη διαμέριση
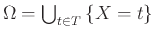
.

Παρατήρηση 12.11
Μετά το Θεώρημα 12.3 είναι φανερό πως η συνθήκες
(12.6) και (12.8)
δεν είναι τίποτε άλλο από τη συνθήκη
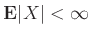 (η μέση τιμή μιας
μη αρνητικής ΤΜ υπάρχει πάντα και είναι πεπερασμένος αριθμός ή
(η μέση τιμή μιας
μη αρνητικής ΤΜ υπάρχει πάντα και είναι πεπερασμένος αριθμός ή 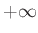 ).
).
Άσκηση 12.20
Όταν αγοράζετε ένα συγκεκριμένο προϊόν υπάρχει πάντα μέσα στη συσκευασία ένα παιχνίδι-έκπληξη.
Υπάρχουν 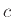 διαφορετικά τέτοια παιχνίδια που μπορεί να βρείτε μέσα στη συσκευασία και όλα
αυτά τα παιχνίδια είναι εξίσου πιθανό να εμφανιστούν.
Αγοράζετε ένα τέτοιο προϊόν κάθε μέρα.
Ποιος είναι ο μέσος αριθμός ημερών που περνάει από τότε που θα βρείτε το
διαφορετικά τέτοια παιχνίδια που μπορεί να βρείτε μέσα στη συσκευασία και όλα
αυτά τα παιχνίδια είναι εξίσου πιθανό να εμφανιστούν.
Αγοράζετε ένα τέτοιο προϊόν κάθε μέρα.
Ποιος είναι ο μέσος αριθμός ημερών που περνάει από τότε που θα βρείτε το 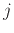 -οστό νέο παιχνίδι
μέχρι να βρείτε το
-οστό νέο παιχνίδι
μέχρι να βρείτε το 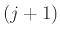 -οστό νέο παιχνίδι;
Ποιος είναι ο μέσος αριθμός ημερών που περνάει έως ότου βρείτε και τα
-οστό νέο παιχνίδι;
Ποιος είναι ο μέσος αριθμός ημερών που περνάει έως ότου βρείτε και τα 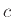 διαφορετικά παιχνίδια;
διαφορετικά παιχνίδια;
Θεώρημα 12.4
Αν οι ΤΜ  και
και 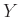 είναι ανεξάρτητες και έχουν μέσες τιμές τότε και η
είναι ανεξάρτητες και έχουν μέσες τιμές τότε και η 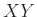 έχει μέση τιμή
και
έχει μέση τιμή
και
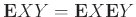 .
.
Απόδειξη.
Έστω
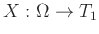
και
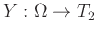
, όπου τα σύνολα
είναι αριθμήσιμα.
Όπως και στην απόδειξη του Θεωρήματος
12.2 ορίζουμε τα ενδεχόμενα
Έχουμε
(
: από ανεξαρτησία των
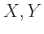
),
οπότε έχουμε δείξει ότι η
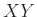
έχει μέση τιμή.
Ομοίως
(
: από ανεξαρτησία των
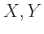
).

Παρατήρηση 12.12
Ομοίως προκύπτει ότι αν οι
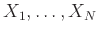 είναι ένα ανεξάρτητο σύνολο από ΤΜ τότε
είναι ένα ανεξάρτητο σύνολο από ΤΜ τότε
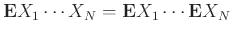 .
.
Παρατήρηση 12.13
Η συνθήκη «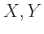 ανεξάρτητες» δε μπορεί να παραλειφθεί στο
Θεώρημα 12.4.
Ας είναι, για παράδειγμα,
ανεξάρτητες» δε μπορεί να παραλειφθεί στο
Θεώρημα 12.4.
Ας είναι, για παράδειγμα, 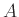 και
και 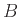 δύο ξένα μεταξύ τους ενδεχόμενα με θετική πιθανότητα
το καθένα, και
δύο ξένα μεταξύ τους ενδεχόμενα με θετική πιθανότητα
το καθένα, και
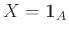 ,
,
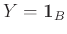 οι αντίστοιχες δείκτριες ΤΜ (δείτε το Παράδειγμα 12.8).
Έχουμε τότε
οι αντίστοιχες δείκτριες ΤΜ (δείτε το Παράδειγμα 12.8).
Έχουμε τότε
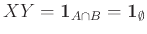 άρα
άρα
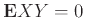 ενώ
ενώ
![$ {\bf E}{X}={{\bf {Pr}}\left[{A}\right]}>0$](img2706.png) και
και
![$ {\bf E}{Y}={{\bf {Pr}}\left[{B}\right]}>0$](img2707.png) .
.
Άσκηση 12.21
Έχουμε 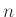 παίκτες που ρίχνουν από ένα ζάρι ο καθένας.
Αν
παίκτες που ρίχνουν από ένα ζάρι ο καθένας.
Αν  είναι το πλήθος των ζευγών που φέρνουν τον ίδιο αριθμό να βρεθεί
η
είναι το πλήθος των ζευγών που φέρνουν τον ίδιο αριθμό να βρεθεί
η
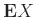 .
.
Άσκηση 12.22
Έχουμε 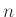 ζευγάρια και από αυτά τα
ζευγάρια και από αυτά τα 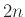 άτομα ένα τυχαίο υποσύνολο μεγέθους
άτομα ένα τυχαίο υποσύνολο μεγέθους 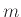 πεθαίνει. Να βρεθεί ο μέσος αριθμών των ζευγαριών που έχουν απομείνει.
πεθαίνει. Να βρεθεί ο μέσος αριθμών των ζευγαριών που έχουν απομείνει.
Άσκηση 12.24
Η ακέραια ΤΜ  έχει πυκνότητα
έχει πυκνότητα 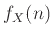 . Εκτελούμε το πείραμα που δίνει τιμή στη
. Εκτελούμε το πείραμα που δίνει τιμή στη  αλλά δε
βλέπουμε την τιμή αυτή. Πρέπει να τη μαντέψουμε. Αν η τιμή που θα πούμε, έστω ο ακέραιος
αλλά δε
βλέπουμε την τιμή αυτή. Πρέπει να τη μαντέψουμε. Αν η τιμή που θα πούμε, έστω ο ακέραιος 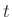 ,
είναι μικρότερη από τη
,
είναι μικρότερη από τη  τότε πληρώνουμε
τότε πληρώνουμε 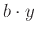 ευρώ, όπου
ευρώ, όπου
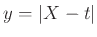 . Αν είναι μεγαλύτερη
τότε πληρώνουμε
. Αν είναι μεγαλύτερη
τότε πληρώνουμε 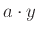 . Οι αριθμοί
. Οι αριθμοί 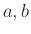 όπως και η συνάρτηση
όπως και η συνάρτηση 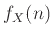 μας είναι γνωστοί.
Πώς πρέπει να επιλέξουμε το
μας είναι γνωστοί.
Πώς πρέπει να επιλέξουμε το 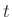 ώστε να έχουμε το μικρότερο δυνατό μέσο κόστος;
ώστε να έχουμε το μικρότερο δυνατό μέσο κόστος;

Σχήμα
12.3: Ο Paul Erdos.

Άσκηση 12.26
Έχουμε 1000 κουτιά στη σειρά (στις θέσεις 1, 2, 3, ..., 1000).
Δείξτε ότι μπορούμε να τα βάψουμε με δύο χρώματα,
π.χ. κόκκινα ή μπλε, με τέτοιο τρόπο ώστε να μην υπάρχει αριθμητική πρόοδος μήκους 20 από κουτιά που να είναι όλα το ίδιο χρώμα.
(Δείτε το Σχήμα 12.4.)
Mihalis Kolountzakis
2015-11-28
![]() είναι οποιαδήποτε διακριτή ΤΜ, με
είναι οποιαδήποτε διακριτή ΤΜ, με ![]() αριθμήσιμο,
τότε η μέση τιμής της ορίζεται από τον τύπο
αριθμήσιμο,
τότε η μέση τιμής της ορίζεται από τον τύπο
![]() .
.![]() , με αριθμήσιμο σύνολο δεικτών
, με αριθμήσιμο σύνολο δεικτών ![]() ,
αποτελούν διαμέριση του δειγματικού χώρου
,
αποτελούν διαμέριση του δειγματικού χώρου ![]() και έχουν την ιδιότητα ότι η ΤΜ
και έχουν την ιδιότητα ότι η ΤΜ ![]() είναι σταθερή
σε κάθε
είναι σταθερή
σε κάθε ![]() με τιμή
με τιμή ![]() τότε
τότε
![$\displaystyle {\bf E}{X} = \sum_{s \in S} c_s {{\bf {Pr}}\left[{A_s}\right]}.
$](img2624.png)
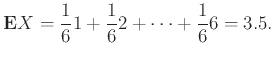
![]() , αν υπάρχει, είναι ένας κυρτός συνδυασμός
των τιμών της
, αν υπάρχει, είναι ένας κυρτός συνδυασμός
των τιμών της ![]() . Κυρτός συνδυασμός κάποιων αριθμών (ή διανυσμάτων)
. Κυρτός συνδυασμός κάποιων αριθμών (ή διανυσμάτων)
![]() είναι μια ποσότητα της μορφής
είναι μια ποσότητα της μορφής
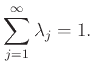
![]() είναι πάντα μη αρνητική και η σειρά
(12.6) ή (12.8)
αποκλίνουν (ισούνται με
είναι πάντα μη αρνητική και η σειρά
(12.6) ή (12.8)
αποκλίνουν (ισούνται με ![]() ), τότε θα θεωρούμε
), τότε θα θεωρούμε
![]() .
.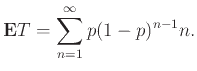
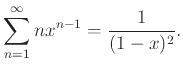
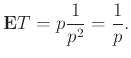
![$\displaystyle {\bf E}{X} = \sum_{s \in T_1} s {{\bf {Pr}}\left[{A_s}\right]} = \sum_{s\in T_1} s \sum_{t \in T_2} {{\bf {Pr}}\left[{C_{s,t}}\right]},
$](img2664.png)
![$\displaystyle {\bf E}{Y} = \sum_{t \in T_2} s {{\bf {Pr}}\left[{B_t}\right]} = \sum_{t\in T_2} t \sum_{s \in T_1} {{\bf {Pr}}\left[{C_{s,t}}\right]},
$](img2665.png)
![$\displaystyle \lambda {\bf E}{X} + \mu {\bf E}{Y} = \sum_{s \in T_1, t \in T_2} {{\bf {Pr}}\left[{C_{s,t}}\right]} (\lambda s+ \mu t)
= {\bf E}{Z},
$](img2666.png)
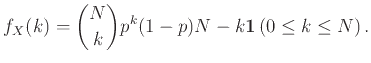
![]() , ο αριθμός των ατόμων, που παίρνουν το δικό τους καπέλο.
Ας είναι
, ο αριθμός των ατόμων, που παίρνουν το δικό τους καπέλο.
Ας είναι ![]() ,
,
![]() , οι ΤΜ
, οι ΤΜ
![]() το άτομο
το άτομο ![]() παίρνει το δικό του καπέλο).
(Οι ΤΜ
παίρνει το δικό του καπέλο).
(Οι ΤΜ ![]() δεν είναι ανεξάρτητες. Γιατί;)
Είναι φανερό ότι
δεν είναι ανεξάρτητες. Γιατί;)
Είναι φανερό ότι
![]() σαν άθροισμα άλλων απλουστέρων, και μάλιστα δεικτριών, ΤΜ είναι ένα
πολύ χρήσιμο εργαλείο στη λύση προβλημάτων.
σαν άθροισμα άλλων απλουστέρων, και μάλιστα δεικτριών, ΤΜ είναι ένα
πολύ χρήσιμο εργαλείο στη λύση προβλημάτων.![$\displaystyle \sum_{t\in T} {\left\vert{f(t)}\right\vert} {{\bf {Pr}}\left[{X=t}\right]} < \infty,
$](img2683.png)
![$\displaystyle {\bf E}{f(X)} = \sum_{t\in T} f(t) {{\bf {Pr}}\left[{X=t}\right]}.
$](img2684.png)
![$\displaystyle \sum_{s \in T_1, t \in T_2} {\left\vert{st}\right\vert} {{\bf {Pr}}\left[{C_{s,t}}\right]}$](img2691.png)
![$\displaystyle \sum_{s \in T_1, t \in T_2} {\left\vert{st}\right\vert} {{\bf {Pr}}\left[{X=s}\right]} {{\bf {Pr}}\left[{Y=t}\right]} \dagger$](img2692.png)
![$\displaystyle \sum_{s \in T_1} {\left\vert{s}\right\vert} {{\bf {Pr}}\left[{X=s...
...cdot \sum_{t \in T_2} {\left\vert{t}\right\vert} {{\bf {Pr}}\left[{Y=t}\right]}$](img2693.png)
![$\displaystyle \sum_{s \in T_1, t \in T_2} st {{\bf {Pr}}\left[{C_{s,t}}\right]}$](img2696.png)
![$\displaystyle \sum_{s \in T_1, t \in T_2} st {{\bf {Pr}}\left[{X=s}\right]} {{\bf {Pr}}\left[{Y=t}\right]} \ddagger$](img2697.png)
![$\displaystyle \sum_{s \in T_1} s {{\bf {Pr}}\left[{X=s}\right]} \cdot \sum_{t \in T_2} t {{\bf {Pr}}\left[{Y=t}\right]}$](img2698.png)
![]() .
Αυτή είναι η ποσότητα
.
Αυτή είναι η ποσότητα
![]() και έχουμε
και έχουμε
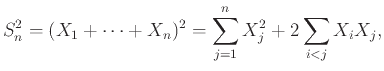
![]() βήματα αν και μόνο αν
έχει επιλεγεί για εναλλαγή ένα άρτιο αριθμό φορών.
βήματα αν και μόνο αν
έχει επιλεγεί για εναλλαγή ένα άρτιο αριθμό φορών.
![]() κορυφές (
κορυφές (![]() σημεία δηλ. που όλα ενώνονται με όλα τα άλλα, με πλήθος ακμών
σημεία δηλ. που όλα ενώνονται με όλα τα άλλα, με πλήθος ακμών
![]() )
και ότι κάθε ακμή του μπορεί να βαφεί κόκκινη ή μπλε.
Δείξτε ότι μπορείτε να επιλέξετε τα χρώματα των ακμών έτσι ώστε το πλήθος των
μονοχρωματικών τριγώνων που σχηματίζονται να είναι το πολύ
)
και ότι κάθε ακμή του μπορεί να βαφεί κόκκινη ή μπλε.
Δείξτε ότι μπορείτε να επιλέξετε τα χρώματα των ακμών έτσι ώστε το πλήθος των
μονοχρωματικών τριγώνων που σχηματίζονται να είναι το πολύ
![]() .
.