1.8 Πληθάριθμος. Αριθμήσιμα και μη άπειρα σύνολα.

Ορισμός 1.20   (Ισοδύναμα σύνολο. Πληθάριθμος.) Δύο σύνολα $A, B$ λέμε ότι είναι ισοδύναμα ή ότι έχουν τον ίδιο πληθάριθμο αν υπάρχει 1-1 και επί συνάρτηση $f:A\longrightarrow{B}$. Γράφουμε

$$A\sim{B} \eta' \char93 A=\char93 B \eta' {\left\vert{A}\right\vert}={\left\vert{B}\right\vert}.$$

Λέμε ότι το σύνολο $A$ έχει μικρότερο πληθάριθμο από το σύνολο $B$ αν υπάρχει συνάρτηση $f:A\longrightarrow{B}$ η οποία είναι 1-1 αλλά τα $A$ και $B$ δεν είναι ισοδύναμα. Γράφουμε

$${\left\vert{A}\right\vert} < {\left\vert{B}\right\vert} \eta' \char93 A<\char93 B.$$

Εύκολα μπορούμε να διαπιστώσουμε ότι η σχέση μεταξύ συνόλων $\sim$, όπως την ορίσαμε παραπάνω, είναι σχέση ισοδυναμίας, δηλαδή ικανοποιεί τις τρεις ιδιότητες:

1. $A\sim{A}$,
2. Αν $A\sim{B}$ τότε $B\sim{A}$,
3. Αν $A\sim{B}$ και $B\sim{C}$ τότε $A\sim{C}$.

Παράδειγμα 1.19   Έστω $A=\{1,2,3\}$, $B=\{a,b,c\},C=\{1,2\}$. Τότε

$$\char93 A=\char93 B, {\left\vert{C}\right\vert}<{\left\vert{B}\right\vert}.$$

Αν γράψουμε όλες τις συναρτήσεις απο το $C\longrightarrow{B}$, θα δούμε ότι καμία δέν είναι επί.

Γιά πεπερασμένα σύνολα, το αν είναι ισοδύναμα ή ίδιου πληθαρίθμου μπορούμε να το βρούμε μετρώντας τα στοιχεία τους. Τα πράγματα είναι τελείως διαφορετικά για άπειρα σύνολα, όπως θα δούμε στο επόμενο παράδειγμα και γι' αυτό τον λόγο έχουμε εισαγάγει τον προηγούμενο ορισμό για την σύγκριση των πληθαρίθμων των συνόλων και δεν είπαμε απλά ότι δύο σύνολα είναι ισοδύναμα αν έχουν τον ίδιο αριθμό στοιχείων. Αυτό το τελευταίο έχει νοήμα να το λέμε μόνο για πεπερασμένα σύνολα.

Παράδειγμα 1.20   Έστω ${{\mathbb{N}}}=\{1,2,3,\ldots\}$ και $A=\{2,4,6,\ldots\}$. Εύκολα βλέπουμε ότι η συνάρτηση $f:{{\mathbb{N}}}\longrightarrow{A}$.$f(x)=2x$ είναι 1-1 και επί. Άρα

$${{\mathbb{N}}}\sim{A}.$$

Στο Παράδειγμα 1.20 βλέπουμε ότι ένα άπειρο σύνολο μπορεί να είναι ισοδύναμο με ένα γνήσιο υποσυνολό του, πράγμα το οποίο δε συμβαίνει με τα πεπερασμένα σύνολα. Αυτή είναι χαρακτηριστική ιδιότητα των απείρων συνόλων, όπως θα δούμε.

Θεωρούμε τα αρχικά τμήματα των φυσικών αριθμών,

$$I_{1}=\{1\},I_{2}=\{1,2\}, \ldots, I_{n}=\{1,2,3,...,n\}, \ldots.$$

Ορισμός 1.21   (Πεπερασμένο σύνολο, άπειρο σύνολο) Ένα σύνολο $A$ λέγεται πεπερασμένο αν είναι ισοδύναμο με κάποιο αρχικό τμήμα των φυσικών αριθμών. Αν $A\sim{I_{n}}$ τότε λέμε ότι ο πληθάριθμος ή το πλήθος στοιχείων του $A$ ισούται με $n$ και γράφουμε $\char93 A=n$ ή $\mid{A}\mid=n$.

Αν ένα σύνολο δεν είναι πεπερασμένο τότε λέγεται άπειρο.

Γιά τα άπειρα σύνολα ισχύει το επόμενο θεώρημα.

Θεώρημα 1.3  

α)

Ένα σύνολο είναι άπειρο αν και μόνο αν είναι ισοδύναμο με κάποιο υποσυνολό του.

β)

Αν $A$ είναι ένα άπειρο σύνολο, τότε ισχύει

$$\mid{{\mathbb{N}}}\mid=\mid{A}\mid \eta' \mid{{\mathbb{N}}}\mid<\mid{A}\mid.$$

(Δηλαδή το μκρότερου πληθαρίθμου άπειρο σύνολο είναι το σύνολο των φυσικών αριθμών.)

γ)

Αν $A$ είναι ένα άπειρο σύνολο και $B \subset A$ με $\mid{B}\mid<\mid{A}\mid$, τότε

$$\mid{A \setminus B}\mid=\mid{A}\mid.$$

Η απόδειξη του παραπάνω θεωρήματος μπορεί να βρεθεί σε ένα οποιδήποτε βιβλίο Θεωρίας Συνόλων, π.χ. στο [5] και δεν περιγράφεται εδώ.

Ορισμός 1.22   (Αριθμήσιμο σύνολο) Ένα σύνολο λέγεται άπειρα αριθμήσιμο αν είναι ισοδύναμο με το σύνολο των φυσικών αριθμών ${{\mathbb{N}}}$. Ένα σύνολο λέγεται αριθμήσιμο αν είναι άπειρα αριθμήσιμο ή πεπερασμένο. Λέγεται μη αριθμήσιμο ή υπεραριθμήσιμο αν δεν είναι αριθμήσιμο.

Παρατήρηση 1.1  

1. Αποδεικνύεται ότι
   $${\left\vert{{\mathbb{N}}}\right\vert} < {\left\vert{{\mathbb{R}}}\right\vert} = {\left\vert{I}\right\vert},$$
   όπου $I$ ένα οποιοδήποτε διάστημα, π.χ. $I=[0,1]$, ή $I=(-2,7]$ ή $I=(1,\infty)$, κ.λ.π. Με άλλα λόγια το ${{\mathbb{R}}}$ είναι άπειρο μη αριθμήσιμο ή, όπως αλλιώς το λέμε, υπεραριθμήσιμο σύνολο.
2. Τα σύνολα $A$ που είναι ισοδύναμα με το ${{\mathbb{R}}}$, λέμε ότι έχουν την ισχύ του συνεχούς. Γράφουμε
   $${\left\vert{A}\right\vert} = c$$
   σε αυτή την περίπτωση.

   Επομένως όλα τα διαστήματα $I\subseteq{{\mathbb{R}}}$ έχουν την ισχύ του συνεχούς.

3. Ο Cantor, ο οποίος ήταν ένας από τους θεμελιωτές της θεωρίας συνόλων, διατύπωσε τον ισχυρισμό, ο οποίος είναι γνωστός ως υπόθεση του συνεχούς:

   «Δεν υπάρχει σύνολο $A$ ώστε να ισχύει ${\left\vert{{\mathbb{N}}}\right\vert} < {\left\vert{A}\right\vert} < {\left\vert{{\mathbb{R}}}\right\vert}$.»

   Το 1963 αποδείχθηκε ότι η υπόθεση του συνεχούς είναι ανεξάρτητη από τα άλλα αξιώματα της θεωρίας συνόλων. Θυμίζουμε ότι το ίδιο συμβαίνει στην Ευκλείδια Γεωμετρία, όπου το αξίωμα της παραλληλίας είναι ανεξάρτητο από τα υπόλοιπα αξιώματα.

Για τα αριθμήσιμα σύνολα αποδεικνύεται το επόμενο θεώρημα.

Θεώρημα 1.4  

α)

Όλα τα υποσύνολα ενός αριθμήσιμου συνόλου είναι αριθμήσιμα σύνολα.

β)

Ας είναι $\{X_{i}\}_{i\in{I}}$ μια οικογένεια συνόλων με σύνολο δεικτών $I$ αριθμήσιμο και $X_{i}$ αριθμήσιμα για κάθε $i\in{I}$. Τότε η ένωση $\bigcup_{i\in{I}}X_{i}$ είναι αριθμήσιμο σύνολο.

Άσκηση 1.13   Αποδείξτε το Θεώρημα 1.4.

Υπόδειξη: Για να δείξουμε ότι ένα σύνολο είναι αριθμήσιμο πρέπει να περιγράψουμε τα στοιχεία του ως μια ακολουθία (όχι απαραίτητα μόνο μια φορά το καθένα). Υποθέστε λοιπόν, π.χ. για το (α) ότι ένα σύνολο $E$ είναι αριθμήσιμο (και άρα έχετε μια ακολουθία που απαρτίζεται από τα στοιχεία του) και για ένα σύνολο $A \subseteq E$ περιγράψτε πώς από την ακολουθία των στοιχείων του $E$ θα πάρετε μια ακολουθία που θα απαριθμεί όλα τα στοιχεία του $A$. Για το (β) έχετε τα στοιχεία του κάθε $X_i$ ως μια ακολουθία ${\left\{{x^i_j: j\in{\mathbb{N}}}\right\}}$. Δείξτε πώς από αυτές τις (αριθμήσιμες σε πλήθος) ακολουθίες θα πάρετε μια ακολουθία που θα περιέχει τα στοιχεία όλων των $X_i$, για κάθε $i \in I$.

Παράδειγμα 1.21   Το ${{\mathbb{N}}}\times{{\mathbb{N}}}$ είναι αριθμήσιμο.

Παρατηρούμε ότι το ${{\mathbb{N}}}$ είναι η ένωση των διαδοχικών διαστημάτων (πού αποτελούν επίσης διαμέριση του ${{\mathbb{N}}}$):

$$B_{1}=\{1\}, B_{2}=\{2,3\}, B_{3}=\{4,5,6\}, B_4 = {\left\{{7, 8, 9, 10}\right\}}, \ldots.$$

Επίσης το ${{\mathbb{N}}}\times{{\mathbb{N}}}$ είναι η ένωση των παρακάτω ξένων ανα δύο συνόλων (διαγώνια αρίθμηση του ${{\mathbb{N}}}\times{{\mathbb{N}}}$):

$$Z_{1} =\{(1,1)\},$$

$$Z_{2} =\{(2,1),(1,2)\},$$

$$Z_{3} =\{(3,1),(2,2),(1,3)\},$$

$$Z_4 = {\left\{{(4,1), (3,2), (2,3), (1, 4)}\right\}},$$

$$\ldots$$

Οπότε η συνάρτηση $f$ που ορίζεται από τον παρακάτω τύπο, αφού πρώτα γράψουμε το τυχόν $k \in {\mathbb{N}}$ στη μορφή

$$k=\frac{n(n-1)}{2}+l,$$

με $l \in {\left\{{0, 1, \ldots, n-1}\right\}}$,

$$f:k \rightarrow f(k) = (n-l+1,l),$$

για $n=1,2,...$, είναι 1-1 και επί.

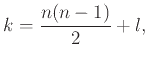
Ανάλογα μπορεί να αποδειχθεί ότι το καρτεσιανό γινόμενο πεπερασμένου πλήθους παραγόντων,

$$X_{1}\times{X_{2}}\times\cdots\times{X_{n}},$$

οποιωνδήποτε αριθμησίμων συνόλων $X_{1},X_{2},...,X_{n}$ είναι αριθμήσιμο.

Αντίθετα, το καρτεσιανό γινόμενο απείρου πλήθους συνόλων (άπειρα από τα οποία δεν είναι μονοσύνολα) δεν είναι αριθμήσιμο [5].

Επίσης εύκολα βλέπουμε ότι το ${{\mathbb{Z}}}$ είναι αριθμήσιμο και, αφού έχουμε δει ότι

$${{\mathbb{Q}}}=\{(a,b)=\frac{a}{b}:a\in{{\mathbb{Z}}},b\in{{\mathbb{N}}}\}\subset{{\mathbb{Z}}}\times{{\mathbb{Z}}},$$

έπεται από το προηγούμενο θεώρημα ότι και το ${{\mathbb{Q}}}$ είναι αριθμήσιμο.

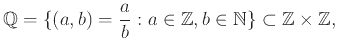
Τελικά από το Θεώρημα 1.4 παίρνουμε ότι το σύνολο των αρρήτων ${{\mathbb{R}}}\setminus {{\mathbb{Q}}}$ είναι υπεραριθμήσιμο αφού, αν δεν ήταν, το ${\mathbb{R}}= {\mathbb{Q}}\cup ({\mathbb{R}}\setminus{\mathbb{Q}})$ θα ήταν κι αυτό αριθμήσιμο.