11.2 Δειγματικοί χώροι, ενδεχόμενα, η πιθανότητά τους

Δοθέντος ενός πειράματος που θέλουμε να μελετήσουμε πιθανοθεωρητικά η πρώτη δουλειά που πρέπει να γίνει είναι να καταλάβουμε ποια ακριβώς είναι τα δυνατά αποτελέσματα αυτού του πειράματος.

Ορισμός 11.1   (Δειγματικός χώρος) Δειγματικός χώρος $\Omega$ ενός πειράματος ονομάζεται το σύνολο των δυνατών αποτελεσμάτων του.

Αν σταματήσουμε εδώ τότε φυσικά δεν έχουμε κάνει τίποτα που θα μας βοηθήσει στην πιθανοθεωρητική ανάλυση αφού έχουμε μόνο μιλήσει για τα δυνατά αποτελέσματα και όχι για τα πιθανά. Γι΄ αυτό το λόγο σε κάθε στοιχείο του δειγματικού χώρου αντιστοιχίζουμε ένα αριθμό $p$ που δηλώνει πόσο πιθανό είναι το στοιχείο αυτό να εμφανιστεί.

Ορισμός 11.2   Έστω $\Omega={\left\{{\omega_1,\omega_2,\ldots}\right\}}$ ένας πεπερασμένος ή αριθμήσιμος δειγματικός χώρος ενός πειράματος. Ονομάζουμε κατανομή πιθανότητας στον $\Omega$ μια συνάρτηση $p:\Omega\to[0,1]$ με την ιδιότητα

$$\sum_{j=1}^{{\left\vert{\Omega}\right\vert}} p(\omega_j) = 1.$$ (11.2)

Εδώ ${\left\vert{\Omega}\right\vert}$ συμβολίζει τον πληθάριθμο του συνόλου ${\left\vert{\Omega}\right\vert}$.

Ο λόγος που που περιοριζόμαστε, προς το παρόν, σε αριθμήσιμους δειγματικούς χώρους, αφήνοντας έξω από τη μελέτη μας πειράματα όπως αυτό της §11.1.5 όπου ο δειγματικός χώρος είναι αυτός των πραγματικών αριθμών (υπεραριθμήσιμος) είναι ότι το αξίωμα (11.2) πρέπει να αντικατασταθεί με κάτι άλλο και η συνάρτηση $p$ δεν είναι πια μια συνάρτηση στα στοιχεία του $\Omega$. Από δώ και στο εξής θα μιλάμε αποκλειστικά για αριθμήσιμους δειγματικούς χώρους εκτός από ορισμένες περιπτώσεις οπότε και θα το ξεκαθαρίζουμε.

Παράδειγμα 11.1   Ο δειγματικός χώρος του τιμίου (έχει δηλ. ίδια πιθανότητα να έρθει κορώνα ή γράμματα) νομίσματος (δες §11.1.1) είναι ο $\Omega = {\left\{{K, \Gamma}\right\}}$. Η κατανομή πιθανότητας στον $\Omega$ είναι η $p(K) = p(\Gamma) = 1/2$.

Παράδειγμα 11.2   Για το τίμιο ζάρι της §11.1.2 έχουμε $\Omega={\left\{{1,2,3,4,5,6}\right\}}$ και η κατανομή πιθανότητας δίδεται από τη συνάρτηση $p:\Omega\to[0,1]$ που είναι σταθερή στον $\Omega$, έχουμε δηλ. $p(1)=p(2)=p(3)=p(4)=p(5)=p(6)=1/6$. Η τιμή 1/6 προκύπτει από την (11.2) και την παραδοχή (τιμιότητα) που κάναμε ότι όλες οι τιμές είναι ισοπίθανες.

Ορισμός 11.3   (Ομοιόμορφη κατανομή) Μια κατανομή πιθανότητας $p:\Omega\to[0,1]$ σε ένα δειγματικό χώρο $\Omega$ λέγεται ομοιόμορφη αν είναι σταθερή στο $\Omega$.

Με βάση τον προηγούμενο ορισμό μπορούμε να λέμε ότι το τίμιο νόμισμα και το τίμιο ζάρι έχουν και τα δύο την ομοιόμορφη κατανομή, πάνω βέβαια σε διαφορετικούς δειγματικούς χώρους.

Παράδειγμα 11.3   Στο παράδειγμα της §11.1.4 έχουμε $\Omega = {\mathbb{N}}\cup {\left\{{\infty}\right\}} = {\left\{{1,2,3,\ldots,\infty}\right\}}$. Προσέξτε εδώ ότι η τιμή $\infty$ είναι δυνατή τιμή για το πείραμα: είναι θεωρητικά δυνατό ένα ζευγάρι να μην κάνει ποτέ αγόρι οπότε θα αποκτήσει (εις το διηνεκές) άπειρα το πλήθος κορίτσια.

Η κατανομή πιθανότητας γι'αυτό το παράδειγμα δίνεται από τη συνάρτηση $p:\Omega\to[0,1]$

$$p(\omega) = \left\{\begin{array}{ll} 0 & \alpha\nu \omega=\i... ...\\ 2^{\omega} & \alpha\lambda\lambda\iota\omega\varsigma \end{array}\right.$$

Θα το αποδείξουμε αυτό αργότερα. Πρός το παρόν το μόνο που είναι εύκολο να δούμε είναι ότι $p(1)=1/2$ αφού κάνει η οικογένεια συνολικά μόνο ένα παιδί μόνο αν το πρώτο παιδί είναι αγόρι, και αυτό συμβαίνει με πιθανότητα 1/2.

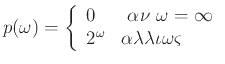
Παρ' ότι η τιμή $\omega=\infty$ είναι δυνατή, εφ' όσον έχει πιθανότητα 0 μπορούμε να την αγνοήσουμε. Με άλλα λόγια, όσον αφορά την πιθανοθεωρητική ανάλυση του πειράματος, στην οποία εν γένει αγνοούμε πράγματα που έχουν πιθανότητα ίση με 0 να συμβούν, μπορούμε να θεωρούμε ότι ο δειγματικός χώρος είναι απλά ο $\Omega' = {\mathbb{N}}$.

Ορισμός 11.4   (Ενδεχόμενα) Ενδεχόμενο ονομάζεται ένα οποιοδήποτε υποσύνολο του δειγματικού χώρου, ένα οποιοδήποτε δηλ. στοιχείο του ${\mathcal{P}}(\Omega)$.

Σε σχέση με ένα πείραμα θα λέμε ότι το ενδεχόμενο $A \subseteq \Omega$ ισχύει αν το αποτέλεσμα του πειράματος ανήκει στο $A$.

Άσκηση 11.2   Αν ${\left\vert{\Omega}\right\vert} = n<\infty$ δείξτε ότι ${\left\vert{{\mathcal{P}}(\Omega)}\right\vert} = 2^n$.

Με τη βοήθεια της κατανομής πιθανότητας $p:\Omega\to[0,1]$ ορίζουμε τώρα τη συνολοσυνάρτηση (δηλ. μια συνάρτηση που ορίζεται πάνω σε σύνολα). της πιθανότητας, που επίσης θα ονομάζουμε κατανομή πιθανότητας, ως εξής.

Ορισμός 11.5   (Συνολοσυνάρτηση πιθανότητας) Αν $\Omega$ δειγματικός χώρος με κατανομή πιθανότητας $p:\Omega\to[0,1]$ ορίζουμε τη συνάρτηση ${\mathbb{P}}:{\mathcal{P}}(\Omega) \to [0,1]$ με

$${{\bf {Pr}}\left[{A}\right]} = \sum_{a \in A} p(a).$$ (11.3)

Με άλλα λόγια η πιθανότητα ${{\bf {Pr}}\left[{A}\right]}$ ενός ενδεχομένου $A \subseteq \Omega$ προκύπτει αν προσθέσουμε τις τιμές $p(a)$ για όλα τα στοιχεία του $A$.

Παράδειγμα 11.4   Στο παράδειγμα του ζαριού (§11.1.2) το ενδεχόμενο $A = {\left\{{2,4,6}\right\}}$ ισχύει μετά την εκτέλεση του πειράματος αν το αποτέλεσμα είναι άρτιο. Έχουμε

$${{\bf {Pr}}\left[{A}\right]} = p(2)+p(4)+p(6) = \frac{1}{6}+\frac{1}{6}+\frac{1}{6} = 1/2.$$

Παράδειγμα 11.5   Στο παράδειγμα της §11.1.4 το ενδεχόμενο $A = {\left\{{1,2,3}\right\}}$ ισχύει αν η οικογένεια αποκτήσει τελικά μέχρι και τρία παιδιά. Έχουμε

$${{\bf {Pr}}\left[{A}\right]} = p(1)+p(2)+p(3) = \frac{1}{2}+\frac{1}{4}+\frac{1}{8} = 7/8.$$

Άσκηση 11.3   Στο πείραμα της §11.1.4 έστω $A = {\left\{{2k: k=1,2,3,\ldots}\right\}}$ το ενδεχόμενο η οικογένεια να αποκτήσει άρτιο αριθμό παιδιών. Υπολογίστε την ${{\bf {Pr}}\left[{A}\right]}$.

Υπόδειξη: Χρησιμοποιήστε την Άσκηση 1.20.

Παρατήρηση 11.1   Έστω $A$ και $B$ δύο ενδεχόμενα. Τότε το να ζητήσουμε να ισχύει το ενδεχόμενο $A \cup B$ είναι σα να ζητάμε να ισχύει ένα τουλάχιστον από τα $A$ και $B$ (μπορεί και τα δύο). Το να ζητήσουμε να ισχύει το ενδεχόμενο $A \cap B$ είναι σα να ζητάμε να ισχύουν και τα δύο ενδεχόμενα $A$ και $B$.

Άσκηση 11.4   Στο παράδειγμα της §11.1.4 έστω $A={\left\{{1,\ldots,10}\right\}}$ και $B = {\left\{{3k: k\in{\mathbb{N}}}\right\}}$ δύο ενδεχόμενα. Περιγράψτε τι σημαίνει το κάθε ένα από αυτά όπως και το τι σημαίνουν τα ενδεχόμενα $A \cap B$ και $A \cup B$.

Άσκηση 11.5   Στο παράδειγμα της §11.1.3 γράψτε ποια στοιχεία απαρτίζουν το ενδεχόμενο το δεύτερο νόμισμα να δείξει κάτι διαφορετικό από το πρώτο και βρείτε την πιθανότητά του.

Άσκηση 11.6   Σε ένα κουτί μέσα βρίσκονται τρείς βώλοι, ένας κόκκινος, ένας πράσινος κι ένας μπλέ. Το πείραμά μας συνίσταται στο να τραβήξουμε ένα βώλο, να σημειώσουμε το χρώμα του, να τον επανατοποθετήσουμε μέσα στο κουτί, να τραβήξουμε πάλι ένα βώλο και να σημειώσουμε και αυτού το χρώμα.

Ποιος είναι ο δειγματικός χώρος του πειράματος; Ποια η κατανομή πιθανότητας στα στοιχεία του αν όλοι οι βώλοι που είναι μέσα στο κουτί είναι εξίσου πιθανό να τραβηχτούν κάθε φορά;

Απαντήστε στο ίδιο ερώτημα αν το πείραμα τροποιηθεί ως εξής: αφού τραβήξουμε πρώτο βώλο, δεν τον επανατοποθετούμε στο κουτί, αλλά απλά τραβάμε και τον δεύτερο από τους δύο εναπομείναντες.

Ορισμός 11.6   (Επεκτεταμένοι φυσικοί αριθμοί) Το σύνολο των επεκτεταμένων φυσικών αριθμών είναι το

$$\overline{{\mathbb{N}}} = {\mathbb{N}}\cup {\left\{{\infty}\right\}} = {\left\{{1, 2, 3, \ldots, \infty}\right\}}.$$

Όταν λοιπόν λέμε $n \in \overline{{\mathbb{N}}}$ εννοούμε ότι ο αριθμός $n$ είναι είτε ένας φυσικός αριθμός είτε το $\infty$. Π.χ., αν έχουμε ένα άθροισμα

$$\sum_{n=1}^N a_n$$

όπου $N \in \overline{{\mathbb{N}}}$, εννούμε ότι είτε μιλάμε για πεπερασμένο άθροισμα είτε για άπειρο.

Θεώρημα 11.1   Η συνολοσυνάρτηση πιθανότητας έχει τις εξής ιδιότητες ( $m \in \overline{{\mathbb{N}}}$):

1. ${{\bf {Pr}}\left[{\emptyset}\right]} = 0$, ${{\bf {Pr}}\left[{\Omega}\right]} = 1$.
2. ${{\bf {Pr}}\left[{A^c}\right]} = 1-{{\bf {Pr}}\left[{A}\right]}$, για κάθε ενδεχόμενο $A$.
3. (Προσθετικότητα) Αν $A_1, A_2, \ldots, A_m$ είναι ξένα μεταξύ τους ενδεχόμενα τότε

   $${{\bf {Pr}}\left[{\bigcup_{j=1}^m A_j}\right]} = \sum_{j=1}^m {{\bf {Pr}}\left[{A_j}\right]}.$$ (11.4)

   
   

4. (Υποπροσθετικότητα) Αν $A_1, A_2, \ldots, A_m$ είναι ενδεχόμενα, όχι απαραίτητα ξένα ανά δύο, τότε

   $${{\bf {Pr}}\left[{\bigcup_{j=1}^m A_j}\right]} \le \sum_{j=1}^m {{\bf {Pr}}\left[{A_j}\right]}.$$ (11.5)

   
   

5. Αν $A$ και $B$ είναι δύο ενδεχόμενα τότε

   $${{\bf {Pr}}\left[{A \cup B}\right]} = {{\bf {Pr}}\left[{A}\right]} + {{\bf {Pr}}\left[{B}\right]} - {{\bf {Pr}}\left[{A \cap B}\right]}.$$ (11.6)

   
   

Απόδειξη. Τα τρία πρώτα είναι άμεσες συνέπειες της (11.3) και της (11.2).

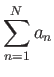
Για το 4 αν χρησιμοποιήσουμε τον ορισμό (11.3) στα δύο μέλη της ανισότητας που έχουμε να αποδείξουμε, παρατηρούμε ότι στο αριστερό μέλος έχουμε ακριβώς τις ποσότητες $p(x)$ για όλα τα $x \in \bigcup_{j=1}^m A_j$, μια φορά την κάθε μια, ενώ στο δεξί μέλος έχουμε τις ίδιες ποσότητες $p(x)$ αλλά τόσες φορές την κάθε μια όσα και τα $A_j$ στα οποία ανήκει το $x$ και πάντως τουλάχιστον μια φορά. Η ανισότητα ισχύει προφανώς μια και $p(x) \ge 0$.

Για το 5 επιχειρηματολογούμε όπως και στο προηγούμενο: στο αριστερό μέλος έχουμε το άθροισμα των $p(x)$ για $x \in A \cup B$ ενώ στο δεξί έχουμε στο άθροισμα ${{\bf {Pr}}\left[{A}\right]} + {{\bf {Pr}}\left[{B}\right]}$ το άθροισμα των ίδιων $p(x)$ με τη διαφορά ότι για τα $x \in A \cap B$ το $p(x)$ εμφανίζεται δύο φορές. Ο προσθετέος $-{{\bf {Pr}}\left[{A\cap B}\right]}$ στο δεξί μέλος διορθώνει αυτή τη διαφορά. $\qedsymbol$

Παρατήρηση 11.2   Είναι πολύ εύκολο να αποδειχθεί (κάντε το) αλλά και πάρα πολύ σημαντικό σε διάφορες αποδείξεις και εφαρμογές ότι αν $A \subseteq B$ τότε ${{\bf {Pr}}\left[{A}\right]} \le {{\bf {Pr}}\left[{B}\right]}$. Επίσης είναι πολύ σημαντική η απλή συνεπαγωγή

$${{\bf {Pr}}\left[{A}\right]} > 0 \Longrightarrow A \neq \emptyset.$$

Αυτή η τελευταία συνεπαγωγή, με την οποία αποδεικνύει κανείς ότι ένα σύνολο δεν είναι κενό αποδεικνύοντας πρώτα ότι η πιθανότητά του δεν είναι 0, αποτελεί το θεμέλιο λίθο της λεγόμενης πιθανοθεωρητικής μεθόδου, παρόμοιας με την υπαρξιακή μέθοδο, στην οποία αποδεικνύει κανείς την ύπαρξη ενός αντικειμένου με πολύ έμμεσο τρόπο, φτιάχνοντας πρώτα ένα πιθανοθεωρητικό μοντέλο γι' αυτό το αντικείμενο που «δουλεύει» με θετική πιθανότητα. Θα έχουμε αργότερα την ευκαιρία να δούμε κάποια παραδείγματα αυτής της μεθόδου.

Άσκηση 11.7   Αν $A_i$, $i=1,\ldots,m$, $m \in \overline{{\mathbb{N}}}$, είναι ενδεχόμενα με ${{\bf {Pr}}\left[{A_i \cap A_j}\right]} = 0$ για κάθε $i \neq j$ δείξτε ότι ισχύει (όπως και όταν $A_i \cap A_j = \emptyset$)

$${{\bf {Pr}}\left[{\bigcup_{i=1}^m A_i}\right]} = \sum_{i=1}^m {{\bf {Pr}}\left[{A_i}\right]}.$$

Άσκηση 11.8   Αν $A,B,C$ ενδεχόμενα δείξτε ότι

$${{\bf {Pr}}\left[{A\cup B \cup C}\right]} = {{\bf {Pr}}\left[{A}\right]}+{{\bf {Pr}}\left[{B}\right]}+{{\bf {Pr}}\left[{C}\right]}$$

$$- {{\bf {Pr}}\left[{A\cap B}\right]} - {{\bf {Pr}}\left[{B ... ...\bf {Pr}}\left[{C \cap A}\right]} + {{\bf {Pr}}\left[{A \cap B \cap C}\right]}.$$

Παράδειγμα 11.6   Έστω $A$ και $B$ δύο ενδεχόμενα, και έστω ότι ${{\bf {Pr}}\left[{A}\right]} = 3/4$ και ${{\bf {Pr}}\left[{B}\right]} = 1/3$. Μόνο με αυτή την πληροφορία τι μπορούμε να συμπεράνουμε για την ποσότητα ${{\bf {Pr}}\left[{A \cap B}\right]}$;

Σίγουρα δε μπορούμε να την υπολογίσουμε ακριβώς. Μπορούμε όμως να έχουμε μια εκτίμηση των ορίων στα οποία κινείται. Συγκεκριμένα μπορούμε να δείξουμε ότι

$$\frac{1}{12} \le {{\bf {Pr}}\left[{A \cap B}\right]} \le \frac{1}{3}.$$

Από το Θεώρημα 11.1 έχουμε

$${{\bf {Pr}}\left[{A \cap B}\right]} = {{\bf {Pr}}\left[{A}\right]... ... {Pr}}\left[{A \cup B}\right]} \le {{\bf {Pr}}\left[{B}\right]} = \frac{1}{3},$$

αφού ${{\bf {Pr}}\left[{A \cup B}\right]} \ge {{\bf {Pr}}\left[{A}\right]}$. Έχουμε δείξει το άνω φράγμα. Για το κάτω φράγμα έχουμε

$${{\bf {Pr}}\left[{A \cap B}\right]} = {{\bf {Pr}}\left[{A}\right]... ...Pr}}\left[{A \cup B}\right]} \ge \frac{3}{4} + \frac{1}{3} - 1 = \frac{1}{12}.$$

Στην τελευταία ανισότητα χρησιμοποιήσαμε απλά ότι ${{\bf {Pr}}\left[{A\cup B}\right]} \le 1$.

Άσκηση 11.9   Έστω ο δειγματικός χώρος $\Omega={\left\{{a,b,c}\right\}}$ με την κατανομή πιθανότητας $p(a) = 1/3$, $p(b) = 5/12$.$p(c)=1/4$. Δείξτε ότι αν πάρουμε τα ενδεχόμενα $A={\left\{{a,b}\right\}}$, $B={\left\{{a}\right\}}$ τότε πιάνεται το άνω όριο στην ανισότητα του Παραδείγματος 11.6.

Φτιάξτε ομοίως ένα άλλο απλό δειγματικό χώρο με την κατάλληλη κατανομή πιθανότητας που να δείχνει ότι και το κάτω όριο της ανισότητας του Παραδείγματος 11.6 μπορεί να πιάνεται σε κάποια παραδείγματα, και άρα ότι η ανισότητα που δείξαμε στο Παρ. 11.6 είναι η καλύτερη δυνατή που μπορεί κανείς να δείξει με τα δεδομένα που μας δόθηκαν.

Το θεώρημα που ακολουθεί, αν και πολύ απλό στην απόδειξή του, θα μας είναι επανειλλημένως χρήσιμο.

Θεώρημα 11.2 (Νόμοι de Morgan)   Αν $A_j$, $j=1,2,\ldots,m$, $m \in \overline{{\mathbb{N}}}$, είναι ενδεχόμενα σε ένα χώρο $\Omega$ τότε έχουμε

$$\left(\bigcup_{j=1}^m A_j\right)^c = \bigcap_{j=1}^m A_j^c$$ (11.7)

και

$$\left(\bigcap_{j=1}^m A_j\right)^c = \bigcup_{j=1}^m A_j^c$$ (11.8)

Απόδειξη. Ας δείξουμε πρώτα την (11.7). Πρόκειται για μια ισότητα συνόλων. Αρκεί λοιπόν να πάρουμε το τυχόν $x$ που ανήκει στο αριστερό μέλος και να δείξουμε ότι ανήκει και στο δεξί μέλος, και επίσης το τυχόν σημείο που ανήκει στο δεξί και να δείξουμε ότι ανήκει στο αριστερό.

Έστω λοιπόν 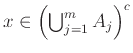$x \in \left(\bigcup_{j=1}^m A_j\right)^c$. Αυτό σημαίνει ότι $x \notin \bigcup_{j=1}^m A_j$ και αυτό με τη σειρά του ότι το $x$ δεν ανήκει σε κανένα $A_j$. Δηλαδή το $x$ ανήκει σε όλα τα $A_j^c$, άρα και στην τομή τους, που είναι και το δεξί μέλος. Ομοίως αποδεικνύεται (άσκηση για τον αναγνώστη) ότι αν το $x$ ανήκει στο δεξί μέλος τότε ανήκει και στο αριστερό.

Έχοντας δείξει την (11.7) μπορούμε να τη χρησιμοποιήσουμε για να δείξουμε την (11.8) (ή μπορούμε να επαναλάβουμε για την (11.8) μια απόδειξη όπως αυτή που δώσαμε για την (11.7)). Πράγματι, παρατηρώντας ότι για κάθε σύνολο $A$ έχουμε $(A^c)^c = A$ και χρησιμοποιώντας στη θέση των συνόλων $A_j$ της (11.7) τα σύνολα $A_j^c$ παίρνουμε ακριβώς την (11.8). $\qedsymbol$

Άσκηση 11.10   Έστω $A,B,C$ ενδεχόμενα. Βρείτε εκφράσεις, χρησιμοποιώντας τα $A,B,C$ και συνολοθεωρητικές πράξεις, για τα ενδεχόμενα:

1. Συμβαίνει μόνο το $A$.
2. Συμβαίνει το $A$ και το $B$ αλλά όχι το $C$.
3. Συμβαίνει τουλάχιστον ένα από τα $A,B,C$.
4. Συμβαίνουν όλα τα $A,B,C$.
5. Συμβαίνει το πολύ ένα από τα $A,B,C$.

Άσκηση 11.11   Δώστε μια συνολοθεωρητική συνθήκη για την πρόταση «Αν συμβαίνει το ενδεχόμενο $A$ τότε συμβαίνει το $B$ ή το $C$».

Επίσης για την πρόταση «δε γίνεται να συμβαίνουν ταυτόχρονα τα $A$ και $B$».

Άσκηση 11.12   Ρίχνουμε ζεύγος τιμίων ζαριών. Ποια τα στοιχεία του ενδεχομένου «τα δυο αποτελέσματα έχουν άθροισμα 4»; Ποια η πιθανότητα του ενδεχομένου αυτού;

Άσκηση 11.13   Οι παίκτες Α και Β παίζουν το εξής παιχνίδι. Ο Α έχει μπροστά του τρία κουτιά, το περιεχόμενο των οποίων βλέπει. Τα δύο κουτιά είναι άδεια και το ένα έχει μέσα ένα νόμισμα. Σκοπός του παίκτη Β είναι να πάρει το νόμισμα.

Οι κανόνες του παιχνιδιού είναι οι εξής: (α) ο Β διαλέγει ένα κουτί και το δείχνει στον Α, (β) ο Α υποχρεούται να επιλέξει ένα άδειο κουτί που δεν είναι αυτό που έδειξε ο Β και να το υποδείξει στον Β, και (γ) ο Β έχει τώρα την ευκαιρία να επιμείνει στην αρχική του επιλογή ή να επιλέξει το άλλο κλειστό κουτί.

Ο Β μπορεί να παίξει με τις εξής τρεις στρατηγικές:

1. Ο Β πάντα εμμένει στην αρχική του επιλογή.
2. Ο Β στρίβει ένα νόμισμα και ξαναεπιλέγει τυχαία ανάμεσα στα δύο εναπομείναντα κλειστά κουτιά.
3. Ο Β πάντα αλλάζει κουτί.

Ποια είναι η πιθανότητα να βρεί ο Β το νόμισμα αν ακολουθήσει κάθε μια από αυτές τις στρατηγικές;

11.2.1 Υπεραριθμήσιμοι δειγματικοί χώροι

Το πείραμα: Έχουμε ένα στρογγυλό στόχο ακτίνας $R$ και πετάμε σε αυτό ένα βέλος.

Το αποτέλεσμα: Το σημείο $(x,y)$ στο οποίο έπεσε το βέλος.

Και πάλι παρατηρούμε, όπως και στο παράδειγμα της §11.1.5 ότι το σύνολο $\Omega$ των δυνατών αποτελεσμάτων, που στην προκειμένη περίπτωση είναι τα σημεία του στόχου, είναι υπεραριθμήσιμο.

Η υπόθεσή μας εδώ είναι ότι δύο ενδεχόμενα $A$ και $B$, υποσύνολα δηλ. του δίσκου, με το ίδιο εμβαδό έχουν την ίδια πιθανότητα να χτυπηθούν. Από την προσθετικότητα που πρέπει να πληροί η συνολοσυνάρτηση της πιθανότητας προκύπτει λοιπόν ότι για κάθε $A \subseteq \Omega$

${{\bf {Pr}}\left[{A}\right]} =$ (εμβαδό του $A$) / $\pi R^2$.

Ποια θα μπορούσε να είναι τότε η κατανομή πιθανότητας $p:\Omega\to[0,1]$ που παράγει την άνω συνολοσυνάρτηση; Η μόνη αποδεκτή λύση συμβατή με την άνω ισότητα θα έπρεπε να είναι η $p(x) \equiv 0$, η οποία φυσικά είναι άχρηστη. Το συμπέρασμα είναι ότι δε μπορεί φυσικά να οριστεί τέτοια συνάρτηση $p$.

Η λύση σε αυτό το πρόβλημα είναι η εξής. Σε δειγματικούς χώρους που είναι υπεραριθμήσιμοι δε χρησιμοποιούμε μια συνάρτηση $p:\Omega\to[0,1]$ για να ορίσουμε τη συνολοσυνάρτηση ${{\bf {Pr}}\left[{\cdot}\right]}$ αλλά ορίζουμε τη συνολοσυνάρτηση αυτή κατ' ευθείαν ως μια συνολοσυνάρτηση που πληροί τα παρακάτω (για να είμαστε ακριβέστεροι θα πρέπει να πούμε ότι συνήθως δεν είναι όλα τα υποσύνολα του δειγματικού χώρου ενδεχόμενα):

Αξιώματα της συνολοσυνάρτησης πιθανότητας

1. $0 \le {{\bf {Pr}}\left[{A}\right]} \le 1$ για κάθε $A$.
2. ${{\bf {Pr}}\left[{\Omega}\right]} = 1$
3. Αν $A_1, A_2, \ldots$ είναι ανά δύο ξένα τότε ${{\bf {Pr}}\left[{\bigcup_j A_j}\right]} = \sum_j {{\bf {Pr}}\left[{A_j}\right]}$.

11.2.2 Ενδεχόμενα με πιθανότητα 0

Ορισμός 11.7   Ένα ενδεχόμενο $A \subseteq \Omega$ λέγεται σχεδόν σίγουρο αν ${{\bf {Pr}}\left[{A^c}\right]} = 0$. Λέγεται σχεδόν αδύνατο αν ${{\bf {Pr}}\left[{A}\right]} = 0$. Λέμε ότι κάτι (ένα ενδεχόμενο δηλ.) συμβαίνει σχεδόν σίγουρα αν συμβαίνει με πιθανότητα 1.

Παράδειγμα 11.7   Στο παράδειγμα της §11.1.4 είναι σχεδόν σίγουρο ότι η οικογένεια θα αποκτήσει πεπερασμένο αριθμό από παιδιά, αφού το συμπληρωματικό ενδεχόμενο, ο αριθμός των παιδιών να είναι $\infty$, έχει πιθανότητα 0.

Παρατήρηση 11.3   Εύκολα βλέπουμε (υποπροσθετικότητα) ότι αν $A_i$, $i=1,2,\ldots,m$, είναι σχεδόν αδύνατα τότε και η ένωσή τους επίσης είναι σχεδόν αδύνατη. Είναι σημαντικό εδώ ότι μιλάμε για μια ένωση από αριθμήσιμα σε πλήθος ενδεχόμενα. Είναι λάθος ότι οποιαδήποτε ένωση ενδεχομένων με πιθανότητα 0 έχει πιθανότητα 0. Αυτό θα φανεί καλύτερα αργότερα όταν θα δούμε μη διακριτούς (υπεραριθμήσιμους) δειγματικούς χώρους.

Άσκηση 11.14   Έστω ακολουθία ενδεχομένων $E_k$.$k \ge 1$, με ${{\bf {Pr}}\left[{E_k}\right]} \to 0$. Δείξτε ότι το ενδεχόμενο $E = \bigcap_{k\ge 1} E_k$ είναι σχεδόν αδύνατο.

Άσκηση 11.15   Έστω σχεδόν σίγουρα ενδεχόμενα $E_k$.$k \ge 1$. Δείξτε ότι σχεδόν σίγουρα ισχύουν όλα τα $E_k$.

Άσκηση 11.16   Έστω ενδεχόμενα $A_k$.$k \ge 1$. Ορίζουμε τα ενδεχόμενα

$$\limsup_k A_k = \bigcap_{k\ge 1} \bigcup_{n\ge k} A_n \kappa\alpha\iota \liminf_k A_k = \bigcup_{k\ge 1} \bigcap_{n\ge k} A_n.$$ (11.9)

Δείξτε ότι το ενδεχόμενο $\limsup_k A_k$ ισχύει ακριβώς όταν ισχύουν άπειρα από τα $A_k$ και το ενδεχόμενο $\liminf_k A_k$ ακριβώς όταν ισχύουν τελικά όλα τα $A_k$, όταν δηλ. υπάρχει κάποιο $k_0$ ώστε να ισχύουν όλα τα $A_k$.$k\ge k_0$.

Άσκηση 11.17   Αν έχουμε ενδεχόμενα $A_k$.$k \ge 1$, με $\sum_{k=1}^\infty {{\bf {Pr}}\left[{A_k}\right]}<\infty$ τότε είναι σχεδόν αδύνατο να ισχύουν άπειρα από τα $A_k$.