Next: 11.4 Ανεξαρτησία ενδεχομένων Up: 11. Εισαγωγή στη διακριτή Previous: 11.2 Δειγματικοί χώροι, ενδεχόμενα, Contents Index
Το πείραμα: Σ' ένα κουτί μέσα βρίσκονται δέκα βώλοι με ονόματα 1 έως 10. Τραβάμε ένα βώλο στην τύχη.
Το αποτέλεσμα: Υποθέτουμε ότι κάποιος μας εγγυάται ότι ![]() .
(Για παράδειγμα, αυτός που εκτελεί το πείραμα ελέγχει αν η συνθήκη
.
(Για παράδειγμα, αυτός που εκτελεί το πείραμα ελέγχει αν η συνθήκη ![]() ισχύει και, αν όχι,
ακυρώνει το πείραμα και το εκτελεί ξανά. Αντίθετα αν η συνθήκη
ισχύει και, αν όχι,
ακυρώνει το πείραμα και το εκτελεί ξανά. Αντίθετα αν η συνθήκη ![]() ισχύει τότε μας αναφέρει
ότι αυτό συμβαίνει.)
Ποιος βώλος
ισχύει τότε μας αναφέρει
ότι αυτό συμβαίνει.)
Ποιος βώλος ![]() τραβήχτηκε.
τραβήχτηκε.
Αν δε βάζαμε τη συνθήκη ![]() θα είχαμε το δειγματικό χώρο
θα είχαμε το δειγματικό χώρο
![]() και τη συνάρτηση πιθανότητας
και τη συνάρτηση πιθανότητας
![]() για
για
![]() .
Εφόσον όμως είναι εγγυημένο ότι
.
Εφόσον όμως είναι εγγυημένο ότι ![]() τα δυνατά αποτελέσματα είναι πλέον τα 5 έως 10,
και εφ' όσον εξακολουθούν να είναι ισοπίθανα έχουν όλα τώρα πιθανότητα 1/6.
τα δυνατά αποτελέσματα είναι πλέον τα 5 έως 10,
και εφ' όσον εξακολουθούν να είναι ισοπίθανα έχουν όλα τώρα πιθανότητα 1/6.
Εφαρμόζοντας τον ορισμό (11.10) και παρατηρώντας ότι
![]() παίρνουμε
παίρνουμε
![]() Έχουμε υπολογίσει την πιθανότητα να βγάλουμε ένα βώλο με αριθμό το πολύ 5 αν γνωρίζουμε ότι
αυτό που τραβήξαμε είναι άρτιο.
Έχουμε υπολογίσει την πιθανότητα να βγάλουμε ένα βώλο με αριθμό το πολύ 5 αν γνωρίζουμε ότι
αυτό που τραβήξαμε είναι άρτιο.
Ας γράψουμε ![]() για το ενδεχόμενο να έχουμε επιλέξει το πρώτο κουτί,
για το ενδεχόμενο να έχουμε επιλέξει το πρώτο κουτί, ![]() για το
δεύτερο και
για το
δεύτερο και ![]() για το τρίτο. Επίσης ας είναι
για το τρίτο. Επίσης ας είναι ![]() το ενδεχόμενο ότι στη θήκη που ανοίγουμε
έχει μαύρο βώλο. Για να έχει και η δεύτερη θήκη του ίδιου κουτιού μαύρο βώλο πρέπει
αναγκαστικά το κουτί να είναι το πρώτο. Πρέπει δηλ. να υπολογίσουμε την ποσότητα
το ενδεχόμενο ότι στη θήκη που ανοίγουμε
έχει μαύρο βώλο. Για να έχει και η δεύτερη θήκη του ίδιου κουτιού μαύρο βώλο πρέπει
αναγκαστικά το κουτί να είναι το πρώτο. Πρέπει δηλ. να υπολογίσουμε την ποσότητα
![$\displaystyle {{\bf {Pr}}\left[{A_1 { \vert }B}\right]}=\frac{{{\bf {Pr}}\left[{A_1 \cap B}\right]}}{{{\bf {Pr}}\left[{B}\right]}}.
$](img2289.png)
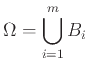
![$\displaystyle \sum_{i=1}^m {{\bf {Pr}}\left[{A \cap B_i}\right]} = {{\bf {Pr}}\...
...]} = {{\bf {Pr}}\left[{A \cap \Omega}\right]}
= {{\bf {Pr}}\left[{A}\right]}.
$](img2301.png)
Με άλλα λόγια, αν και η ποσότητα
![]() δεν έχει πάντα νόημα, η ποσότητα
δεν έχει πάντα νόημα, η ποσότητα
![]() έχει.
έχει.
Δηλ. με πιθανότητα 1 (σχεδόν σίγουρα όπως λέμε στη
Θεωρία Πιθανοτήτων) όποτε γίνει το πείραμα θα ισχύει ακριβώς ένα από τα ![]() .
.
Βρείτε πώς πρέπει να χαλαρώσουμε τη συνθήκη ότι τα ![]() είναι ανά δύο ξένα ώστε να εξακολουθεί να
ισχύει σχεδόν σίγουρα ακριβώς ένα από τα
είναι ανά δύο ξένα ώστε να εξακολουθεί να
ισχύει σχεδόν σίγουρα ακριβώς ένα από τα ![]() σε κάθε έκβαση του πειράματος.
σε κάθε έκβαση του πειράματος.
Ορίζουμε
![]() να είναι τα ενδεχόμενα επιλογής κόκκινου, πράσινου ή μπλέ βώλου.
Αυτά είναι ανά δύο ξένα με πιθανότητες που μας δίδονται:
να είναι τα ενδεχόμενα επιλογής κόκκινου, πράσινου ή μπλέ βώλου.
Αυτά είναι ανά δύο ξένα με πιθανότητες που μας δίδονται:
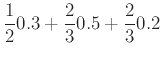 |
|||
Mihalis Kolountzakis 2015-11-28