Next: 11.5 Video Κεφαλαίου Up: 11. Εισαγωγή στη διακριτή Previous: 11.3 Υπό συνθήκη πιθανότητα Contents Index
Γενικότερα αν ![]() .
.![]() , είναι ένα σύνολο ενδεχομένων (το σύνολο
, είναι ένα σύνολο ενδεχομένων (το σύνολο ![]() μπορεί
να είναι και υπεραριθμήσιμο) αυτό θα λέγεται ανεξάρτητο σύνολο ενδεχομένων
αν για κάθε πεπερασμένο πλήθος από αυτά, έστω
μπορεί
να είναι και υπεραριθμήσιμο) αυτό θα λέγεται ανεξάρτητο σύνολο ενδεχομένων
αν για κάθε πεπερασμένο πλήθος από αυτά, έστω
![]() , η πιθανότητα
της τομής τους ισούται με το γινόμενο των πιθανοτήτων τους:
, η πιθανότητα
της τομής τους ισούται με το γινόμενο των πιθανοτήτων τους:
Ο ορισμός αυτός, αν και διαισθητικά ελκυστικότερος, έχει το μειονέκτημα ότι (α) δεν μπορούμε
να τον επικαλεστούμε εκτός αν
![]() , (β) τα
, (β) τα ![]() και
και ![]() δεν εμφανίζονται με συμμετρικό τρόπο
σε αυτόν και (γ) δε γενικεύεται εύκολα σε περισσότερα από δύο ενδεχόμενα.
δεν εμφανίζονται με συμμετρικό τρόπο
σε αυτόν και (γ) δε γενικεύεται εύκολα σε περισσότερα από δύο ενδεχόμενα.
Η ανεξαρτησία αυτών των δύο ενδεχομένων αντικατοπτρίζει το γεγονός ότι οι δύο διαφορετικές ρίψεις του νομίσματος δεν επηρεάζουν η μια την άλλη, είναι όπως λέμε ανεξάρτητες ρίψεις.
Πράγματι
Πώς γενικεύεται το Παράδειγμα 11.12;
Αν έχουμε κάποια ενδεχόμενα ![]() και κάποια
και κάποια ![]() , όλα ανεξάρτητα μεταξύ τους,
και ενδεχόμενα
, όλα ανεξάρτητα μεταξύ τους,
και ενδεχόμενα ![]() και
και ![]() που ορίζονται μέσω των
που ορίζονται μέσω των ![]() και
και ![]() αντιστοιχα, για παράδειγμα
μέσω συνολοθεωρητικών πράξεων όπως στο Παράδειγμα 11.12,
τότε τα
αντιστοιχα, για παράδειγμα
μέσω συνολοθεωρητικών πράξεων όπως στο Παράδειγμα 11.12,
τότε τα ![]() και
και ![]() είναι ανεξάρτητα. Αν και η απόδειξη δεν είναι ιδιαίτερα δύσκολη δε θα
την παρουσιάσουμε εδώ. Θα χρησιμοποιηθεί όμως κατά κόρον.
είναι ανεξάρτητα. Αν και η απόδειξη δεν είναι ιδιαίτερα δύσκολη δε θα
την παρουσιάσουμε εδώ. Θα χρησιμοποιηθεί όμως κατά κόρον.
Ένας τρόπος να εκφραστούμε με ακρίβεια είναι ο εξής. Ονομάζουμε ![]() το ενδεχόμενο να έχουμε κορώνα (Κ)
στην
το ενδεχόμενο να έχουμε κορώνα (Κ)
στην ![]() -οστή ρίψη,
-οστή ρίψη, ![]() . Η υπόθεση ότι οι ρίψεις είναι ανεξάρτητες σημαίνει ότι τα ενδεχόμενα
. Η υπόθεση ότι οι ρίψεις είναι ανεξάρτητες σημαίνει ότι τα ενδεχόμενα
![]() είναι ανεξάρτητα.
είναι ανεξάρτητα.
Τι συνέπειες έχει αυτό; Για παράδειγμα εν θέλουμε να υπολογίσουμε την πιθανότητα του να έχουμε
ΚΚΓ στις τρεις ρίψεις του νομίσματος αυτή είναι η πιθανότητα του ενδεχομένου
![]() και, λόγω της ανεξαρτησίας, έχουμε
και, λόγω της ανεξαρτησίας, έχουμε
Εδώ τα πράγματα περιπλέκονται λίγο σε σχέση με το Παράδειγμα 11.13 μια και σε εκείνο το Παράδειγμα αρκούσε να ξέρουμε το αν φέραμε κορώνα ή όχι για να ξέρουμε το αποτέλεσμα της ρίψης, πράγμα που δεν ισχύει εδώ μια και το πλήθος των δυνατών αποτελεσμάτων μιας ρίψης είναι 6 κι όχι 2.
Ένας τρόπος να θεμελιώσουμε με ακρίβεια την ανεξαρτησία των τριών ρίψεων είναι να ορίσουμε το ενδεχόμενο
![]() .
.![]() ,
,
![]() , να σημαίνει ότι στην
, να σημαίνει ότι στην ![]() -οστή ρίψη έχουμε αποτέλεσμα
-οστή ρίψη έχουμε αποτέλεσμα ![]() ,
και να πούμε ότι για κάθε επιλογή των άνω δεικτών
,
και να πούμε ότι για κάθε επιλογή των άνω δεικτών
![]() τα ενδεχόμενα
τα ενδεχόμενα
![]() είναι ανεξάρτητα.
είναι ανεξάρτητα.
Με αυτό τον τρόπο μπορούμε π.χ. να υπολογίσουμε την πιθανότητα να φέρουμε αποτελέσματα 1,2,3 ως
την πιθανότητα του ενδεχομένου
![]() , που, λόγω της ανεξαρτησίας των τριών,
ισούται με
, που, λόγω της ανεξαρτησίας των τριών,
ισούται με ![]() .
.
Πάντως ο πιο απλός τρόπος να θεμελιώσουμε σωστά την έννοια των ανεξάρτητων αυτών ρίψεων θα μας είναι προσιτός αφού μιλήσουμε για τις τυχαίες μεταβλητές.
Η σύμβαση που θα ακολουθούμε από δω και πέρα στην περιγραφή πειραμάτων κωδικοποιείται στον παρακάτω ορισμό.
Έστωσυνεπάγεται ότι στον προφανή δειγματικό χώρο αυτού του σύνθετου πειράματοςανεξάρτητες ρίψεις ενός νομίσματος.
Δείξτε ότι τα τρία αυτά ενδεχόμενα είναι ανά δύο ανεξάρτητα αλλά όχι και τα τρία μαζί.
Προφανώς τότε ισχύει για κάθε
![]()
Η ανεξαρτησία όμως των γεννήσεων συνεπάγεται ότι τα ενδεχόμενα
![]() είναι
ανεξάρτητα αφού κάθε ένα από αυτά εξαρτάται κι από διαφορετικό πείραμα.
Άρα
είναι
ανεξάρτητα αφού κάθε ένα από αυτά εξαρτάται κι από διαφορετικό πείραμα.
Άρα
Έστω ![]() το ενδεχόμενο να μας έρθει ακριβώς ένα 6, και
το ενδεχόμενο να μας έρθει ακριβώς ένα 6, και ![]() ,
,
![]() , το ενδεχόμενο
να μας έρθει ακριβώς ένα έξι και μάλιστα στη θέση
, το ενδεχόμενο
να μας έρθει ακριβώς ένα έξι και μάλιστα στη θέση ![]() .
Προφανώς τα
.
Προφανώς τα ![]() αποτελούν διαμέριση του
αποτελούν διαμέριση του ![]() , οπότε
, οπότε
![]() .
.
Ορίζουμε τα ενδεχόμενο ![]() , για
, για
![]() , να σημαίνει ότι στην
, να σημαίνει ότι στην ![]() -οστή ρίψη το αποτέλεσμα είναι
-οστή ρίψη το αποτέλεσμα είναι ![]() .
Προφανώς ισχύει
.
Προφανώς ισχύει
![$\displaystyle {{\bf {Pr}}\left[{E_i}\right]} = \left(\frac{5}{6}\right)^9 \frac{1}{6},
$](img2378.png)
Τέλος
![]() .
.
Ας ονομάσουμε ![]() ,
,
![]() , το ενδεχόμενο να μη φέρουμε 6 στην
, το ενδεχόμενο να μη φέρουμε 6 στην ![]() -οστή ρίψη.
Ισχύει φυσικά
-οστή ρίψη.
Ισχύει φυσικά
![]() για κάθε
για κάθε ![]() να μη φέρουμε ποτέ 6;
να μη φέρουμε ποτέ 6;
Ας ονομάσουμε ![]() ,
,
![]() , το ενδεχόμενο να μη φέρουμε 6 στην
, το ενδεχόμενο να μη φέρουμε 6 στην ![]() -οστή ρίψη.
Ισχύει φυσικά
-οστή ρίψη.
Ισχύει φυσικά
![]() για κάθε
για κάθε ![]() .
Επίσης η ακολουθία
.
Επίσης η ακολουθία ![]() είναι ανεξάρτητη αφού κάθε
είναι ανεξάρτητη αφού κάθε ![]() αναφέρεται σε διαφορετική ρίψη.
Τέλος
αναφέρεται σε διαφορετική ρίψη.
Τέλος
![]() , οπότε
, οπότε
![$\displaystyle {{\bf {Pr}}\left[{E}\right]} = \prod_{i=1}^\infty (5/6) = \lim_{N\to\infty} \prod_{i=1}^N (5/6)
= \lim_{N\to\infty} (5/6)^N = 0,
$](img2390.png)
Ορίζουμε πάλι ![]() να είναι το ενδεχόμενο
να είναι το ενδεχόμενο
![]() ,
το ενδεχόμενο δηλ. να μην εμφανιστεί η «απογορευμένη λέξη» αρχίζοντας από την
,
το ενδεχόμενο δηλ. να μην εμφανιστεί η «απογορευμένη λέξη» αρχίζοντας από την ![]() -οστή θέση
της ακολουθίας. Προφανώς ισχύει και πάλι
-οστή θέση
της ακολουθίας. Προφανώς ισχύει και πάλι
![]() . Η ουσιαστική διαφορά με προηγουμένως
είναι ότι τα
. Η ουσιαστική διαφορά με προηγουμένως
είναι ότι τα ![]() δεν αποτελούν πλέον ανεξάρτητη ακολουθία, τουλάχιστον όχι αν δεν το αποδείξουμε, αφού, για παράδειγμα
το
δεν αποτελούν πλέον ανεξάρτητη ακολουθία, τουλάχιστον όχι αν δεν το αποδείξουμε, αφού, για παράδειγμα
το ![]() και
και ![]() ανεφέρονται και τα δύο στη ρίψη υπ' αριθμόν
ανεφέρονται και τα δύο στη ρίψη υπ' αριθμόν ![]() .
.
Ο τρόπος να δείξουμε και πάλι ότι
![]() είναι να παρατηρήσουμε ότι τα ενδεχόμενα
είναι να παρατηρήσουμε ότι τα ενδεχόμενα
![]() ,
,
![]() , είναι ανεξάρτητα, αφού αναφέρονται σε διαφορετικά πειράματα και ότι
, είναι ανεξάρτητα, αφού αναφέρονται σε διαφορετικά πειράματα και ότι
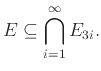
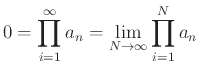
Υπόδειξη: Πάρτε λογαρίθμους και χρησιμοποιήστε την ανισότητα
Υπόδειξη: Χρησιμοποιήστε την Άσκηση 11.32
Η εταιρεία δημοσκοπήσεων έχει μεγάλο πρόβλημα να πραγματοποιήσει αυτή τη δημοσκόπηση. Αν η εταιρεία μπορούσε να μαζέψει ένα τυχαίο δείγμα του κόσμου, π.χ. 10.000 άτομα, σε ένα χώρο, θα μπορούσε εύκολα να τους μοιράσει ανώνυμα ερωτηματολόγια. Οι ερωτούμενοι τότε, καλυπτόμενοι από την ανωνυμία, δε θα είχαν λόγο να απαντήσουν ψέματα και από τις απαντήσεις τους θα προέκυπτε εύκολα η εκτίμηση της πιθανότητας απιστίας.
Όμως το να μαζέψει τόσο κόσμο είναι πολύ ακριβό και αυτή η μέθοδος είναι ανεφάρμοστη. Η εταιρεία δημοσκοπήσεων μπορεί όμως να βγάλει συνεργάτες της έξω οι οποίοι θα μπορούν να σταματάνε τυχαία κόσμο στο δρόμο (ή να επισκέπτονται κόσμο τυχαία στα σπίτια ή τις δουλειές τους) και να τους ρωτάνε. Και πάλι βέβαια, αν σας σταματήσει κάποιος στο δρόμο και σας κάνει τέτοια ερώτηση υπάρχει μεγάλη πιθανότητα ότι δε θα πείτε την αλήθεια (που ξέρετε αν αυτός που σας ρωτάει σας ξέρει ή όχι, κλπ).
Προτείνετε ένα τρόπο να συλλέξετε δεδομένα που θα σας οδηγήσουν στη σωστή εκτίμηση της πιθανότητας απιστίας. Πιο συγκεκριμένα, προτείνετε ένα τρόπο να απαντάει το τυχαίο άτομο μ' ένα ΝΑΙ ή ΟΧΙ, χρησιμοποιώντας κι ένα νόμισμα το οποίο μπορεί να ρίχνει όσες φορές θέλει και του οποίου το αποτέλεσμα μόνο αυτό το άτομο ξέρει. Από τις απαντήσεις αυτές θα πρέπει να μπορείτε να συνάγετε την εκτίμηση της πιθανότητας αλλά δε θα μπορείτε να βγάλετε συμπέρασμα για τις καλοκαιρινές δραστηριότητες κανενός ερωτούμενου. Επίσης αυτό το τελευταίο θα πρέπει να είναι προφανές στους ερωτούμενους.
Υποθέτουμε ότι οι ερωτούμενοι δρουν καλόπιστα και ακολουθούν τις οδηγίες σας.
Επιλέγουμε τους τυχαίους αριθμούς
![]() ομοιόμορφα και ανεξάρτητα από το
ομοιόμορφα και ανεξάρτητα από το ![]() . Δείξτε ότι
. Δείξτε ότι
![$\displaystyle {{\bf {Pr}}\left[{f(X_1,\ldots,X_n) = 0}\right]} \le \frac{d}{\vert S\vert}.
$](img2412.png)
Υπόδειξη: Επαγωγή ως προς ![]() . Μη ξεχνάτε ότι ένα πολυώνυμο μιας μεταβλητής δε μπορεί να έχει περισσότερες ρίζες απ' ό,τι ο βαθμός του.
. Μη ξεχνάτε ότι ένα πολυώνυμο μιας μεταβλητής δε μπορεί να έχει περισσότερες ρίζες απ' ό,τι ο βαθμός του.
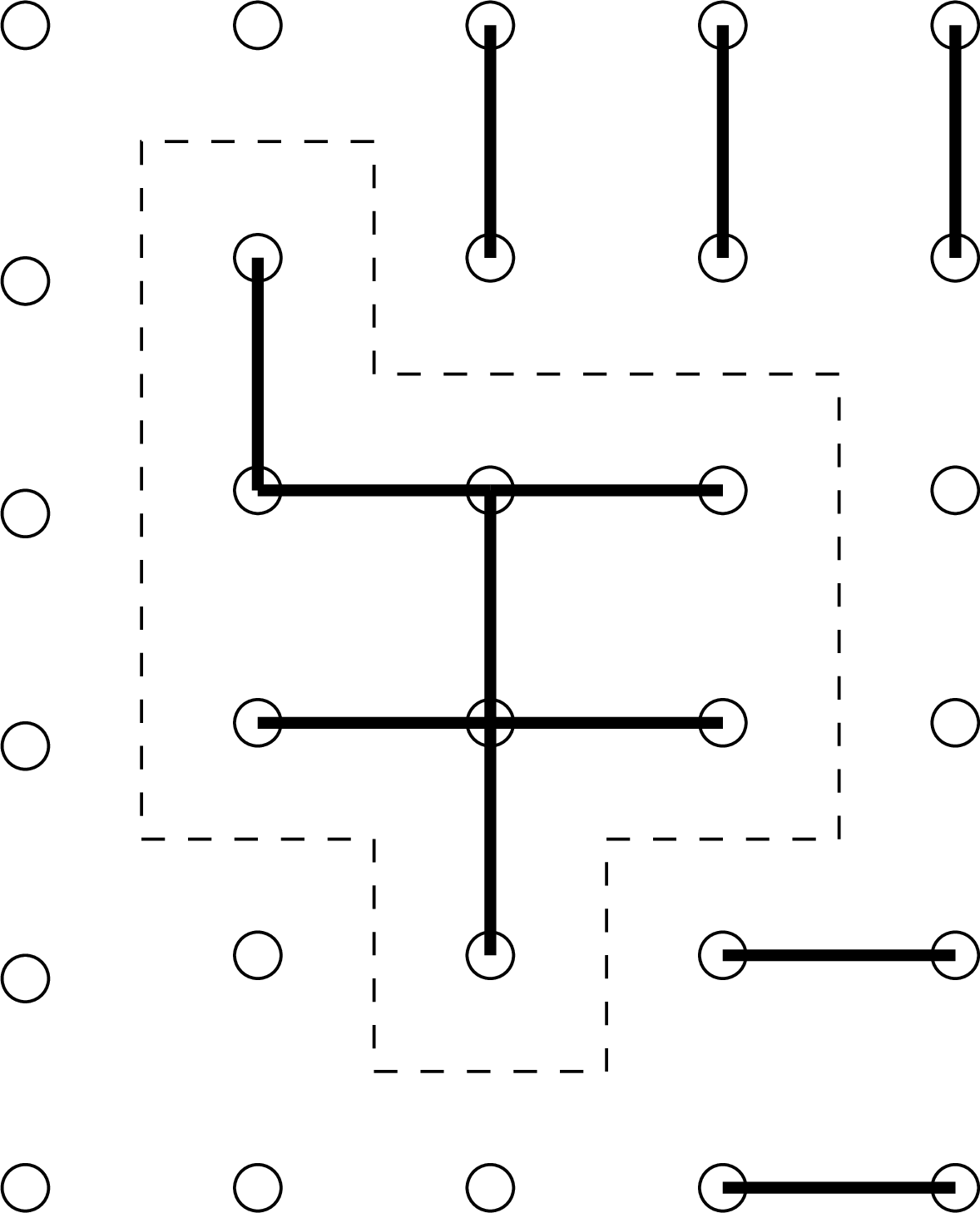
Θεωρήστε το ενδεχόμενο ![]() μετά από τις διαγραφές ακμών να υπάρχει μονοπάτι που ξεκινάει από κάποια κουκίδα
της αριστερής μεριάς και καταλήγει σε κάποια κουκίδα της δεξιάς μεριάς του πίνακα (το μονοπάτι αποτελείται από ακμές που δε σβήστηκαν).
μετά από τις διαγραφές ακμών να υπάρχει μονοπάτι που ξεκινάει από κάποια κουκίδα
της αριστερής μεριάς και καταλήγει σε κάποια κουκίδα της δεξιάς μεριάς του πίνακα (το μονοπάτι αποτελείται από ακμές που δε σβήστηκαν).
Αποδείξτε ότι η πιθανότητα του ![]() είναι αύξουσα συνάρτηση του
είναι αύξουσα συνάρτηση του ![]() .
.
Υπόδειξη: Η δυσκολία σε αυτό το πρόβλημα έγκειται στο ότι προσπαθούμε να συγκρίνουμε δύο πιθανότητες που εμφανίζονται σε δύο
διαφορετικά πειράματα (με μια τιμή του ![]() και με μια μεγαλύτερη τιμή του
και με μια μεγαλύτερη τιμή του ![]() ).
Προσπαθήστε με κάποιο τρόπο να εκφράσετε αυτά τα δύο ενδεχόμενα ως ενδεχόμενα του ίδιου πειράματος.
).
Προσπαθήστε με κάποιο τρόπο να εκφράσετε αυτά τα δύο ενδεχόμενα ως ενδεχόμενα του ίδιου πειράματος.
Mihalis Kolountzakis 2015-11-28