11.1 Πειράματα

11.1.1 Ρίψη νομίσματος

Το πείραμα: Η ρίψη ενός νομίσματος.

Το αποτέλεσμα: Κορώνα (Κ) ή γράμματα (Γ)

Αν υποθέσουμε ότι επαναλαμβάνουμε το πείραμα $N$ φορές τότε περιμένουμε τις μισές από αυτές περίπου το αποτέλεσμα να είναι Κ. Αυτή ακριβώς την έννοια κωδικοποιούμε λέγοντας ότι η πιθανότητα το πείραμα να έχει αποτέλεσμα Κ είναι ίση με 1/2. Η πιθανότητα $p$ δηλ. να φέρει ένα πείραμα ένα αποτέλεσμα Α είναι η αναμενόμενη συχνότητα με την οποία θα εμφανιστεί το αποτέλεσμα Α αν επαναλάβουμε το πείραμα πάρα πολλές φορές. Αν δηλ. το επαναλάβουμε $N$ φορές περιμένουμε το αποτέλεσμα Α να εμφανιστεί περίπου $pN$ φορές. Εύλογο είναι ότι ο αριθμός $p$ πρέπει να είναι ένας πραγματικός αριθμός στο διάστημα $[0,1]$.

11.1.2 Ρίψη ζαριού

Το πείραμα: Η ρίψη ενός ζαριού.

Το αποτέλεσμα: Ένας από τους αριθμούς 1 έως 6.

Αν υποθέσουμε ότι επαναλαμβάνουμε το πείραμα $N$ φορές τότε περιμένουμε το αποτέλεσμα να είναι ο αριθμός 2 με περίπου $N/6$ φορές. Η πιθανότητα δηλ. το αποτέλεσμα να είναι 2 ισούται με 1/6. Το ίδιο είναι και η πιθανότητα το αποτέλεσμα να είναι 1 ή 3 ή οποιοδήποτε άλλο από τα δυνατά αποτελέσματα.

Σε αυτό το παράδειγμα (ζάρι) όπως και στο προηγούμενο (νόμισμα) τα δυνατά αποτελέσματα είναι όλα ισοπίθανα.

Παρατηρήστε επίσης ότι αν αθροίσουμε (είτε στο παράδειγμα του νομίσματος είτε του ζαριού) τις πιθανότητες των δυνατών αποτελεσμάτων θα πάρουμε 1. Αυτό είναι αναμενόμενο με βάση την ερμηνεία που έχουμε προσδώσει στην πιθανότητα ως συχνότητα εμφάνισης του αποτελεσματος: αν επαναλάβουμε το πείραμα $N$ φορές τότε το άθροισμα των συχνοτήτων εμφάνισης των αποτελεσμάτων είναι 1.

11.1.3 Ζεύγος νομισμάτων

Το πείραμα: Ρίχνουμε δύο νομίσματα και παρατηρούμε τι (Κ ή Γ) έφερε το κάθε νόμισμα.

Το αποτέλεσμα: Όλα τα ζεύγη $(x,y)$ όπου τα $x$.$y$ είναι Κ ή Γ.

Ερμηνεύοντας όπως και προηγουμένως την πιθανότητα ενός δυνατού αποτελέσματος ως τη συχνότητα με την οποία εμφανίζεται εύκολα καταλήγουμε ότι οι πιθανότητες των τεσσάρων δυνατών αποτελεσμάτων (Κ,Κ), (Κ,Γ), (Γ,Κ) και (Γ,Γ) πρέπει να είναι όλες ίσες και άρα ίσες με 1/4. Ένας άλλος τρόπος να το σκεφτούμε αυτό είναι να παρατηρήσουμε ότι αν εκτελέσουμε το πείραμα $N$ φορές περιμένουμε περίπου τις μισές από αυτές το πρώτο νόμισμα να έρθει Κ, και περίπου τις μισές από αυτές να έρθει και το δεύτερο νόμισμα Κ, αφού οι ρίψεις των δύο νομισμάτων δεν αλληλοεπηρεάζονται. Άρα η πιθανότητα του αποτελέσματος (Κ,Κ) πρέπει να είναι 1/4.

11.1.4 Αριθμός παιδιών

Το πείραμα: Ένα ζευγάρι κάνει συνεχώς παιδιά μέχρι να κάνει το πρώτο αγόρι, οπότε και σταματάει. Υποθέτουμε ότι σε όλες τις γέννες γεννιέται ένα παιδί κι ότι μπορούν να κάνουν απεριόριστα μεγάλο αριθμό παιδιών.

Το αποτέλεσμα: Ο αριθμός $N$, $N=1,2,3,\ldots$, των παιδιών που κάνει τελικά το ζευγάρι.

Το σύνολο των δυνατών αποτελεσμάτων εδώ είναι άπειρο, αλλά αριθμήσιμο.

Η επίλυση του προβλήματος αυτού συνίσταται στο να υπολογιστεί η πιθανότητα να έχουμε $N=1$, η πιθανότητα να έχουμε $N=2$, κλπ. Για παράδειγμα, είναι πολύ εύκολο να δούμε ότι η πιθανότητα $N=1$ ισούται με $1/2$ (υποθέτουμε εδώ ότι η πιθανότητα γέννησης αγοριού είναι 1/2), αφού $N=1$ όταν και μόνο όταν το πρώτο παιδί που θα γεννηθεί είναι αγόρι. Θα δούμε αργότερα ότι η πιθανότητα να έχουμε $N=k$, για ένα οποιοδήποτε φυσικό αριθμό $k$, ισούται με $2^{-k}$.

Αν το δεχτούμε αυτό τότε επαληθεύουμε εύκολα και πάλι ότι το άθροισμα των πιθανοτήτων για όλα τα δυνατά αποτελέσματα του πειράματος ισούται με 1:

$$\sum_{k=1}^\infty 2^{-k} = 1.$$

Για να δείτε την παραπάνω ισότητα χρησιμοποιήστε την ταυτότητα (άθροισμα άπειρης γεωμετρικής σειράς) για $z=1/2$:

$$\sum_{k=0}^\infty z^k = 1+z+z^2+z^3+\cdots = \frac{1}{1-z},$$ (11.1)

που ισχύει για οποιοδήποτε μιγαδικό αριθμό $z$ με ${\left\vert{z}\right\vert}<1$ (Άσκηση 1.20.)

Άσκηση 11.1   Βρείτε ένα τύπο για το άθροισμα $\sum_{k=0}^{N-1} k z^k = z+2z^2+3z^3+\cdot+(N-1)z^{N-1}$.

Υπόδειξη: Χρησιμοποιήστε την Άσκηση 1.20.

11.1.5 Χρόνος αναμονής

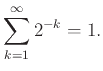
Το πείραμα: Καθόμαστε μπροστά από ένα κατάστημα και μετράμε το χρόνο που περνάει από τη στιγμή που θα μπεί ένας πελάτης μέχρι να μπεί ο επόμενος.

Το αποτέλεσμα: Ένας πραγματικός αριθμός $t\ge 0$.

Σε αντίθεση με τα παραδείγματα του ζαριού και του νομίσματος το πλήθος των δυνατών αποτελεσμάτων σε αυτό πείραμα είναι άπειρο και μάλιστα υπεραριθμήσιμο. Δεν έχει εδώ νόημα να αντιστοιχίσουμε μια πιθανότητα εμφάνισης σε κάθε δυνατό $t$. Εξάλλου είναι φανερό ότι αν επαναλάβουμε το πείραμα αυτό πολλές φορές είναι πρακτικά αδύνατο να παρατηρήσουμε τον ίδιο χρόνο δύο φορές (όχι προσεγγιστικά αλλά ακριβώς). Έχει όμως νόημα να μετρήσουμε πόσες φορές (από τις $N$) ο χρόνος αυτός πέφτει μέσα σε εάν διάστημα, π.χ. ανάμεσα σε 2 και 3 λεπτά. Έχει δηλ. νόημα να μιλήσουμε για την πιθανότητα να συμβεί $2\le t \le 3$.

11.1.6 Ύψος και βάρος

Το πείραμα: Ανοίγουμε τον τηλεφωνικό κατάλογο της πόλης μας και επιλέγουμε ένα τυχαίο άτομο. Το παίρνουμε τηλ. και ρωτάμε το ύψος και το βάρος του.

Το αποτέλεσμα: Δύο πραγματικοί αριθμοί $H$ και $W$. Υποθέτουμε ότι $0 \le H \le 2.5$ (μέτρα) και $0 \le W \le 300$ (κιλά).

Εδώ το σύνολο των δυνατών αποτελεσμάτων είναι τα ζεύγη $(H,W)$, όπου τα $H$ και $W$ πληρούν τις άνω ανισότητες. Όπως και στο Παράδειγμα της §11.1.5 το σύνολο των δυνατών αποτελεσμάτων είναι υπαραριθμήσιμο.