Next: 5.6 Γενικεύσεις της έννοιας Up: 5. Εισαγωγή στη θεωρία Previous: 5.4 Συνεκτικότητα και αποστάσεις Contents Index
Τα δέντρα είναι, κατά κάποιο τρόπο, τα συνεκτικά γραφήματα χωρίς περιττές ακμές.
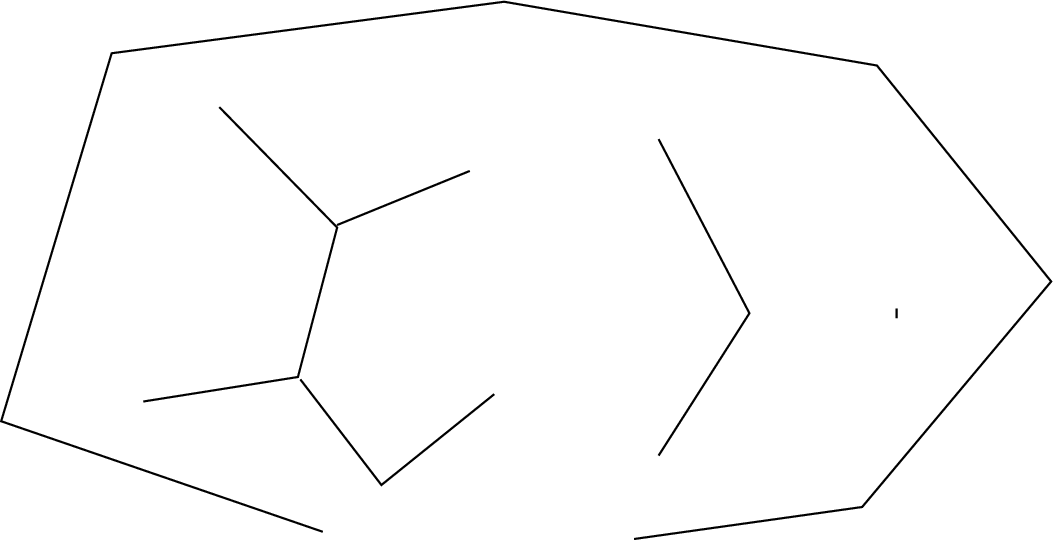
Η δεύτερη ονομασία είναι συμβατή με την πρώτη αφού κάθε τέτοιο γράφημα μπορεί να το δει κανείς σαν το σύνολο των συνεκτικών συνιστωσών του. Αλλά κάθε τέτοια συνεκτική συνιστώσα εξακολουθεί να μην περιέχει κύκλους (αφού είναι υπογράφημα του αρχικού), άρα είναι ένα δέντρο, δηλ. κάθε γράφημα χωρίς κύκλους είναι μια «ξένη» (δηλ. χωρίς μεταξύ τους συνδέσεις) ένωση από δέντρα. Με άλλα λόγια, ένα γράφημα είναι δάσος αν και μόνο είναι μια ένωση από, ασύνδετα μεταξύ τους, δέντρα.
Τα δέντρα έχουν ενδιαφέρον επειδή, κατά κάποια έννοια, είναι τα
«ελάχιστα» συνεκτικά γραφήματα: κάθε συνεκτικό γράφημα ![]() περιέχει ένα υπογράφημα με τις ίδιες κορυφές, συνεκτικό και
χωρίς κύκλους (άρα δέντρο).
(Δείτε το Θεώρημα 5.1.)
περιέχει ένα υπογράφημα με τις ίδιες κορυφές, συνεκτικό και
χωρίς κύκλους (άρα δέντρο).
(Δείτε το Θεώρημα 5.1.)
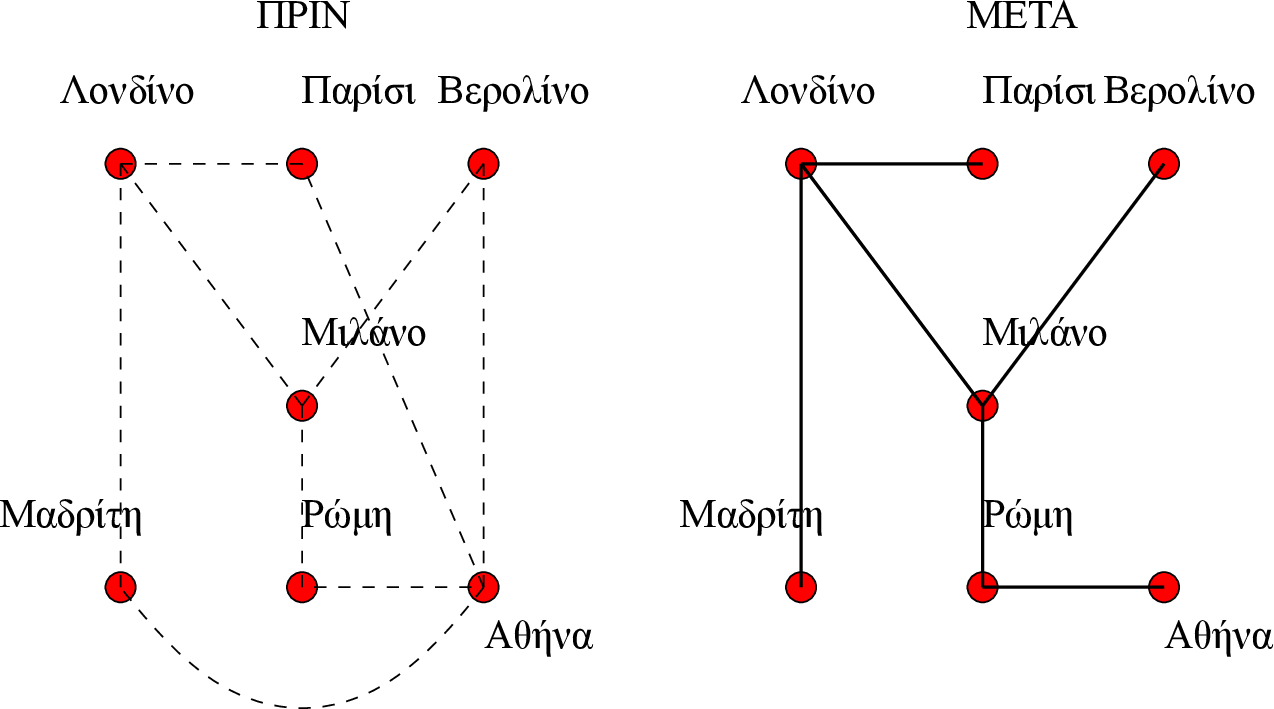
Σε κάποια άσχημη οικονομική συγκυρία η εταιρεία αποφασίζει πως δεν είναι πλέον σε
θέση να εκτελεί τόσο πολλά δρομολόγια και ότι πρέπει να καταργήσει όσο πιο πολλά
μπορεί.
Η εταιρεία δε θα εισαγάγει νέα δρομολόγια, απλώς θα καταργήσει μερικά.
Για λόγους πολιτικής όμως η εταιρεία δε μπορεί να σταματήσει να εξυπηρετεί καμία
από τις ![]() πόλεις που μέχρι τότε εξυπηρετούσε.
Επίσης, προσεγγιστικά, όλες οι πτήσεις κοστίζουν το ίδιο στην εταιρεία,
ανεξάρτητα από την απόσταση.
πόλεις που μέχρι τότε εξυπηρετούσε.
Επίσης, προσεγγιστικά, όλες οι πτήσεις κοστίζουν το ίδιο στην εταιρεία,
ανεξάρτητα από την απόσταση.
Δείχνουμε στο Σχήμα 5.21 τη λύση που επέλεξε τελικά η εταιρεία. Παρατηρήστε ότι:
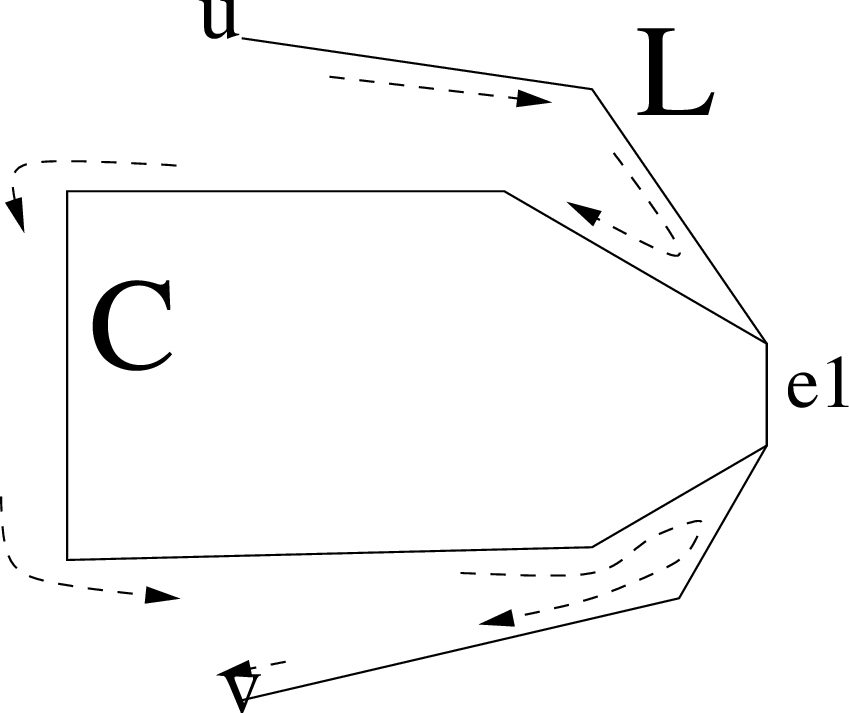
Είναι φανερό ότι, παρά το ότι τώρα πια η ακμή ![]() έχει διαγραφεί,
μπορούμε και πάλι να πάμε από το
έχει διαγραφεί,
μπορούμε και πάλι να πάμε από το ![]() στο
στο ![]() διανύοντας το μονοπάτι
όπως και πριν αλλά όταν θα χρειαστεί να περάσουμε την
διανύοντας το μονοπάτι
όπως και πριν αλλά όταν θα χρειαστεί να περάσουμε την ![]() μπορούμε
να την αντικαταστήσουμε διανύοντας το υπόλοιπο του κύκλου
μπορούμε
να την αντικαταστήσουμε διανύοντας το υπόλοιπο του κύκλου ![]() .
.
Την πράξη αυτή, που μόλις δείξαμε ότι διατηρεί τη συνεκτικότητα, την
ονομάζουμε «σπάσιμου του κύκλου ![]() στην ακμή
στην ακμή ![]() ».
Επαναλαμβάνοντας αυτή την πράξη όσο εξακολουθούν να υπάρχουν κύκλοι
στο γράφημα, και αφού μετά από κάθε τέτοια πράξη οι ακμές λιγοστεύουν
κατά μία, είναι φανερό (εφόσον μιλάμε για πεπερασμένα γραφήματα)
ότι θα φτάσουμε σε ένα ύπογράφημα του
».
Επαναλαμβάνοντας αυτή την πράξη όσο εξακολουθούν να υπάρχουν κύκλοι
στο γράφημα, και αφού μετά από κάθε τέτοια πράξη οι ακμές λιγοστεύουν
κατά μία, είναι φανερό (εφόσον μιλάμε για πεπερασμένα γραφήματα)
ότι θα φτάσουμε σε ένα ύπογράφημα του ![]() με τις ίδιες κορυφές (αυτές
δεν αλλάζουν με την πράξη της διαγραφής της ακμής), συνεκτικό και χωρίς πλέον κύκλους,
δηλ. σε ένα δέντρο.
με τις ίδιες κορυφές (αυτές
δεν αλλάζουν με την πράξη της διαγραφής της ακμής), συνεκτικό και χωρίς πλέον κύκλους,
δηλ. σε ένα δέντρο.
Αν το γράφημα ![]() δεν είναι συνεκτικό εφαρμόζουμε το πρώτο κομμάτι (που
μόλις αποδείξαμε) του Θεωρήματος 5.1 σε κάθε συνεκτική του
συνιστώσα και παίρνουμε έτσι από ένα δένδρο για κάθε συνιστώσα, που την παράγει.
δεν είναι συνεκτικό εφαρμόζουμε το πρώτο κομμάτι (που
μόλις αποδείξαμε) του Θεωρήματος 5.1 σε κάθε συνεκτική του
συνιστώσα και παίρνουμε έτσι από ένα δένδρο για κάθε συνιστώσα, που την παράγει.
![]()
Το επόμενο θεώρημα μας λέει ότι, αντίθετα με τα γενικά γραφήματα, το πλήθος των ακμών σε ένα δέντρο είναι πλήρως καθορισμένο από το πλήθος των κορυφών του.
Ισχυρισμός: Υπάρχει κορυφή τουμε βαθμό
.
Εστω ότι όλες οι κορυφές έχουν βαθμό ![]() (αφού καμία δεν
έχει βαθμό 0 λόγω συνεκτικότητας). Μπορούμε τότε να βρούμε
μονοπάτια οσουδήποτε μεγάλου μήκους στο
(αφού καμία δεν
έχει βαθμό 0 λόγω συνεκτικότητας). Μπορούμε τότε να βρούμε
μονοπάτια οσουδήποτε μεγάλου μήκους στο ![]() στα οποία ποτέ δεν
εμφανίζεται κάτι της μορφής
στα οποία ποτέ δεν
εμφανίζεται κάτι της μορφής
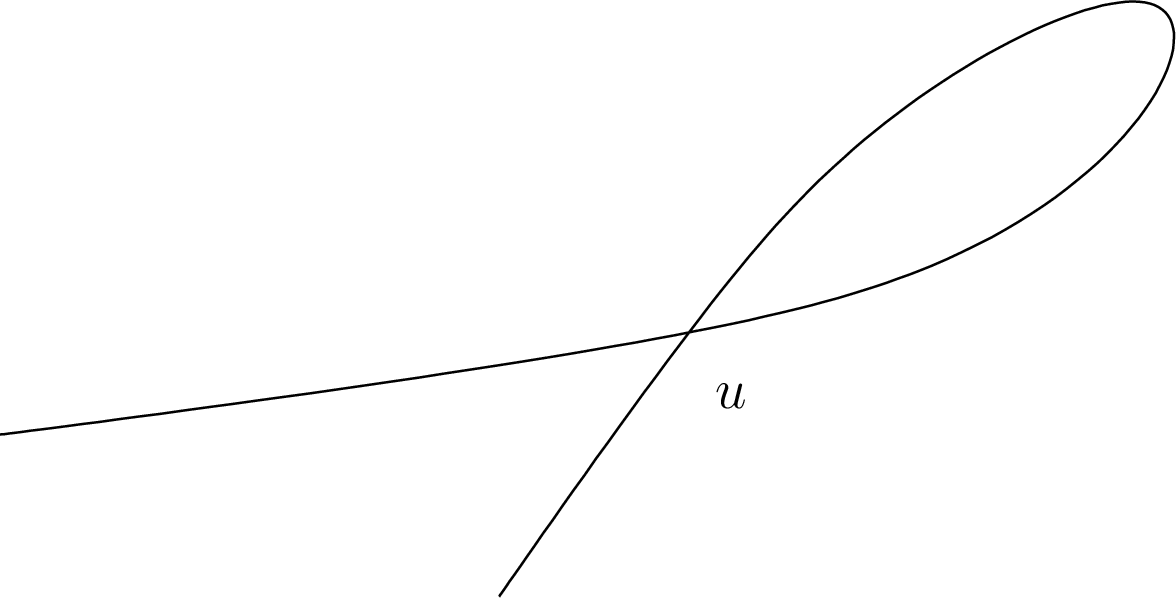
Η κατάσταση απεικονίζεται στο Σχήμα 5.23.
Η επιπλέον ιδιότητα αυτή της ![]() συνεπάγεται ότι στο κύκλωμα
που απεικονίζεται στο σχήμα πάνω από το
συνεπάγεται ότι στο κύκλωμα
που απεικονίζεται στο σχήμα πάνω από το ![]() δεν υπάρχει άλλη
επαναλαμβανόμενη κορυφή ή ακμή, άρα αυτό το κύκλωμα είναι
κύκλος, πράγμα που απαγορεύεται σε δέντρο, και έχουμε
αποδείξει τον ισχυρισμό.
(Δείτε και την Άσκηση 5.23.)
δεν υπάρχει άλλη
επαναλαμβανόμενη κορυφή ή ακμή, άρα αυτό το κύκλωμα είναι
κύκλος, πράγμα που απαγορεύεται σε δέντρο, και έχουμε
αποδείξει τον ισχυρισμό.
(Δείτε και την Άσκηση 5.23.)
Εστω λοιπόν
![]() και ορίζουμε το υπογράφημα
και ορίζουμε το υπογράφημα ![]() του
του ![]() που
επάγεται από τις υπόλοιπες κορυφές
που
επάγεται από τις υπόλοιπες κορυφές
![]() ,
σβήνουμε δηλ. την
,
σβήνουμε δηλ. την ![]() και τη μοναδική ακμή που καταλήγει στην
και τη μοναδική ακμή που καταλήγει στην ![]() .
(Δείτε Σχήμα 5.24.)
.
(Δείτε Σχήμα 5.24.)
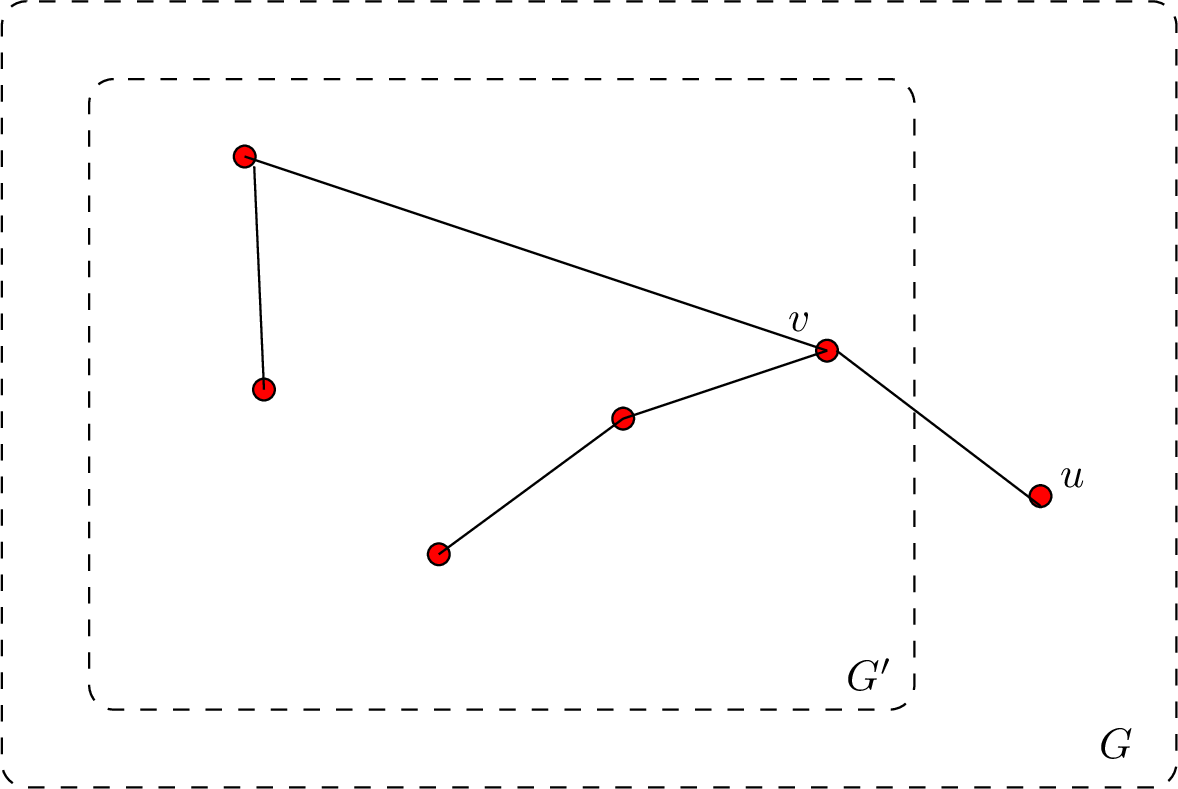
Ως υπογράφημα, το ![]() προφανώς δεν έχει κύκλους και εξακολουθεί να είναι
συνεκτικό αφού είναι φανερό ότι, επειδή η
προφανώς δεν έχει κύκλους και εξακολουθεί να είναι
συνεκτικό αφού είναι φανερό ότι, επειδή η ![]() έχει βαθμό
έχει βαθμό ![]() , δεν μπορεί
να χρησιμοποιθεί για τη σύνδεση δύο άλλων κορυφών.
Αλλά το
, δεν μπορεί
να χρησιμοποιθεί για τη σύνδεση δύο άλλων κορυφών.
Αλλά το ![]() έχει
έχει ![]() κορυφές και από την επαγωγική μας υπόθεση
έχει συνεπώς
κορυφές και από την επαγωγική μας υπόθεση
έχει συνεπώς ![]() ακμές. Αρα το
ακμές. Αρα το ![]() έχει
έχει ![]() (αυτές του
(αυτές του ![]() συν αυτή που καταλήγει στην
συν αυτή που καταλήγει στην ![]() ).
).
![]()
Υπόδειξη: Εφαρμόστε το Θεώρημα 5.2 σε κάθε δέντρο του δάσους (δηλ. σε κάθε συνεκτική συνιστώσα του γραφήματος).
Υπόδειξη: Σε κάθε συνεκτικό γράφημα και για κάθε δύο κορυφές του υπάρχει μονοπάτι μεταξύ τους χωρίς επαναλαμβανόμενες ακμές (π.χ. κάθε μονοπάτι που τις ενώνει και είναι ελάχιστου μήκους). Θα πρέπει να δείξετε ότι αν το γράφημα είναι δέντρο τότε αυτό το μονοπάτι είναι μοναδικό. Επίσης, για το αντίστροφο, ότι αν σε κάποιο συνεκτικό γράφημα ισχύει η μοναδικότητα για κάθε ζεύγος κορυφών του τότε αυτό είναι δέντρο.
Για να δείξετε τη μοναδικότητα (στην περίπτωση που το γράφημα είναι δέντρο) υποθέστε, αντίθετα με αυτό που θέλετε να αποδείξετε,
ότι οι κορυφές ![]() του δέντρου
του δέντρου ![]() συνδέονται με δύο διαφορετικά μονοπάτια
συνδέονται με δύο διαφορετικά μονοπάτια
![]() μεταξύ τους. Κάθε ένα από τα
μεταξύ τους. Κάθε ένα από τα
![]() δεν περιέχει επαναλαμβανόμενες ακμές.
δεν περιέχει επαναλαμβανόμενες ακμές.
Η εύκολη περίπτωση είναι όταν καμιά ακμή του ![]() δεν υπάρχει στο
δεν υπάρχει στο ![]() .
Σε αυτή την περίπτωση το κύκλωμα που δημιουργείται αρχίζοντας από την κορυφή
.
Σε αυτή την περίπτωση το κύκλωμα που δημιουργείται αρχίζοντας από την κορυφή ![]() , ακολουθώντας το
, ακολουθώντας το ![]() ως την κορυφή
ως την κορυφή ![]() , και
απιστρέφοντας στην κορυφή
, και
απιστρέφοντας στην κορυφή ![]() ακολουθώντας το
ακολουθώντας το ![]() ανάποδα, δεν είναι απλά ένα κύκλωμα αλλά κύκλος, δεν περιέχει δηλ.
επαναλαμβανόμενες ακμές. Αυτό αντιφάσκει με το ότι το γράφημα μας είναι δέντρο (=συνεκτικό και χωρίς κύκλους).
ανάποδα, δεν είναι απλά ένα κύκλωμα αλλά κύκλος, δεν περιέχει δηλ.
επαναλαμβανόμενες ακμές. Αυτό αντιφάσκει με το ότι το γράφημα μας είναι δέντρο (=συνεκτικό και χωρίς κύκλους).
Γενικά μπορεί όμως μια ακμή του ![]() να υπάρχει και στο
να υπάρχει και στο ![]() οπότε ο κύκλος που θα πρέπει να βρούμε για να έχουμε αντίφαση
δε μπορεί να είναι η προηγούμενος και χρειάζεται κάπως προσεκτική δουλειά.
οπότε ο κύκλος που θα πρέπει να βρούμε για να έχουμε αντίφαση
δε μπορεί να είναι η προηγούμενος και χρειάζεται κάπως προσεκτική δουλειά.
Υπόδειξη: Αν το δέντρο μας έχει ![]() κορυφές τότε έχει ακριβώς
κορυφές τότε έχει ακριβώς ![]() ακμές.
Μετά την πρόσθεση μιας ακμής θα έχει
ακμές.
Μετά την πρόσθεση μιας ακμής θα έχει ![]() ακμές και παραμένει φυσικά συνεκτικό, άρα δεν παραμένει δέντρο
και το νέο μας γράφημα θα περιέχει κάποιο κύκλο. Θα πρέπει να δείξετε ότι περιέχει μόνο ένα κύκλο.
ακμές και παραμένει φυσικά συνεκτικό, άρα δεν παραμένει δέντρο
και το νέο μας γράφημα θα περιέχει κάποιο κύκλο. Θα πρέπει να δείξετε ότι περιέχει μόνο ένα κύκλο.
Εύκολα έχουμε τώρα:
Υπόδειξη: Πόρισμα 5.1.
(α) Δείξτε ότι μια ακμή είναι γέφυρα αν και μόνο αν δεν περιέχεται σε κανένα κύκλο.
(β) Δείξτε ότι κάθε ακμή του ![]() είναι γέφυρα αν και μόνο αν το
είναι γέφυρα αν και μόνο αν το ![]() είναι δέντρο.
είναι δέντρο.
Mihalis Kolountzakis 2015-11-28