Εισαγωγή
Μια απλοποιημένη θεωρία σφαλμάτων
Γραφικές παραστάσεις

Ο άνθρωπος αρχίζει να αποκτά γνώση για τον φυσικό κόσμο γύρω του, από τη στιγμή που αρχίζει να καταγράφει τα φυσικά φαινόμενα και να τα επεξεργάζεται ανάλογα με τις ικανότητές του. Η γνώση αυτή προέρχεται από την παρατήρηση και αυξάνεται συνεχώς μέχρι σήμερα (η καύση ενός κορμού δέντρου, ο βρασμός ενός υγρού, η ηλέκτριση με τριβή, οι κινήσεις των αστέρων). Η μεγάλη στιγμή είναι όταν ο άνθρωπος, με δική του πρωτοβουλία, αποφασίζει να αναπαραστήσει ο ίδιος μια μεταβολή, δηλαδή να κάνει πείραμα. (Για το πού και πότε έγινε αυτό υπάρχουν πολλές απόψεις που δεν εμπίπτουν, όμως, στον σκοπό αυτού του βιβλίου.)

Στις μέρες μας η γνώση για τον φυσικό κόσμο έχει δύο πηγές: α) την παρατήρηση, β) το πείραμα. Γενικά, μπορούμε να πούμε ότι οι σκοποί ενός πειράματος είναι:
  • η ανάλυση δεδομένων, η εξαγωγή συμπερασμάτων και η διατύπωση μιας (ίσως προσωρινής) θεωρίας που περιλαμβάνει τους νόμους στους οποίους υπακούν τα φαινόμενα του πειράματος,

  • η σχεδίαση και διεξαγωγή πειράματος με σκοπό την επαλήθευση μιας προτεινόμενης θεωρίας η οποία ισχυρίζεται ότι μπορεί να ερμηνεύσει κάποια φαινόμενα ή παρατηρήσεις (Καραμπαρμπούνης κ.ά., 2012).
Σήμερα στα Εκπαιδευτικά Ιδρύματα υπάρχουν ερευνητικά εργαστήρια που εξυπηρετούν τους παραπάνω σκοπούς. Παράλληλα, υπάρχουν και τα εκπαιδευτικά εργαστήρια Φυσικής που απευθύνονται σε νέους και ίσως άπειρους από πειραματικές διεργασίες φοιτητές, οπότε οι στόχοι τους διαφέρουν από αυτούς των ερευνητικών εργαστηρίων. Σε γενικές γραμμές οι στόχοι ενός εκπαιδευτικού εργαστηρίου Φυσικής είναι:
  • η γνωριμία με μερικά από τα όργανα του εργαστηρίου,
  • η εξάσκηση στη μεθοδολογία εκτέλεσης ενός πειράματος και στην επαλήθευση μερικών γνωστών νόμων της Φυσικής,
  • η κατανόηση της αβεβαιότητας (σφάλμα) που υπάρχει σε κάθε μέτρηση,
  • η παρουσίαση του τελικού αποτελέσματος, ώστε να περιλαμβάνει τις αβεβαιότητες του πειράματος,
  • η σύγκριση των αποτελεσμάτων με την ήδη γνωστή αληθινή/παραδεκτή τιμή του μετρούμενου μεγέθους, όπως αυτή προκύπτει από τη σχετική βιβλιογραφία,
  • η δημιουργία γραφικών παραστάσεων και η παρουσίαση των πειραματικών αποτελεσμάτων.
Το εργαστήριο Φυσικής για το οποίο γίνεται λόγος στο συγκεκριμένο βιβλίο διαρκεί δύο διδακτικές ώρες και υλοποιείται μία φορά την εβδομάδα στη διάρκεια ενός εξαμήνου. Το εξάμηνο (ιδανικά) αποτελείται από 14 εβδομάδες. Βασική μας θέση στη λειτουργία του συγκεκριμένου εργαστηρίου είναι οι φοιτητές που το παρακολουθούν να έρχονται σε επαφή τόσο με απλά όργανα, όσο και με σύγχρονες ψηφιακές συσκευές μέτρησης. Επίσης, με την απλοποιημένη Θεωρία Σφαλμάτων που παρουσιάζουμε, ελπίζουμε να γίνει μια καλή αρχή στο σημαντικό θέμα της αμφιβολίας για κάθε πειραματικό αποτέλεσμα. Αργότερα, αξιοποιώντας πιο σύνθετες μαθηματικές γνώσεις, οι φοιτητές μπορούν, αν θέλουν, να προχωρήσουν σε επιστημονικά και ερευνητικά εργαστήρια.

Αβεβαιότητα μετρήσεων
Μια εργασία στο εργαστήριο Φυσικής είναι η μέτρηση ενός μεγέθους, δηλαδή η σύγκρισή του με ένα ομοειδές μέγεθος που γίνεται με τη βοήθεια ενός κατάλληλου οργάνου. Το αποτέλεσμα της μέτρησης δίνεται από το όργανο. Το όργανο μπορεί να είναι αναλογικό ή ψηφιακό. Εσύ βλέπεις και καταγράφεις την απάντηση η οποία είναι ένα αποτέλεσμα συνεργασίας του παρατηρητή με το χρησιμοποιούμενο όργανο. Από αυτή τη συνεργασία προκύπτουν οι αβεβαιότητες της μέτρησης, αυτό που ισοδύναμα θα ονομάζουμε σφάλμα της μέτρησης.
Ο συνδυασμός ανθρώπου ‒ οργάνου ‒ περιβάλλοντος έχει ως αποτέλεσμα να διαφέρουν μεταξύ τους οι μετρήσεις του ίδιου μεγέθους στο ίδιο πείραμα. Έτσι, σου δημιουργείται η αίσθηση του σφάλματος, δηλαδή της διαφοράς μεταξύ της μέτρησης που έκανες και της αληθινής τιμής του ίδιου μεγέθους. Στο εκπαιδευτικό εργαστήριο Φυσικής η αληθινή τιμή με το σφάλμα της υπάρχει, επειδή κάποιος άλλος την έχει υπολογίσει πριν από εσένα ή επειδή δέχεσαι ότι υπάρχει, οπότε την ονομάζεις αποδεκτή τιμή. Η πραγματική τιμή δεν είναι δυνατόν να προσδιοριστεί σε μία σειρά μετρήσεων και έτσι προσεγγίζεται με τη μέση τιμή της και με το σφάλμα της.
Παράδειγμα:
Θέλεις να μετρήσεις την περίοδο ενός μαθηματικού εκκρεμούς με ένα χρονόμετρο. Σύντομα βλέπεις ότι οι μετρήσεις διαφέρουν μεταξύ τους. Γιατί συμβαίνει αυτό; Σε αυτό το αποτέλεσμα έχουν συμβάλει πολλοί παράγοντες:
  • ο άνθρωπος: αντανακλαστικά κτλ,
  • το όργανο: είναι καλά ρυθμισμένο, έχει κάποια μικρή βλάβη, μετάθεση του μηδενός κτλ,
  • το περιβάλλον: δονήσεις, ρεύματα αέρα ή ηλεκτρικά, πάτωμα αγώγιμο ή μονωτικό κτλ.
Τους πιθανούς τύπους σφαλμάτων και τους τρόπους αντιμετώπισής τους θα τους γνωρίσεις παρακάτω.

Είδη σφαλμάτων

  • Ακούσια λάθη

Είναι τα σφάλματα που οφείλονται στον παρατηρητή ο οποίος πιθανόν:
  • Παρατηρεί άλλο και καταχωρεί άλλο.
  • Ακούει άλλο και καταχωρεί άλλο.
  • Κάνει λάθος στις πράξεις.
  • Κάνει σφάλμα παράλλαξης.
    (Σφάλμα παράλλαξης είναι αυτό που συμβαίνει όταν σε ένα αναλογικό όργανο κοιτάμε τη βελόνα υπό λάθος γωνία. Διαβάζουμε ή εκτιμούμε έτσι ένα λάθος αριθμό. Διόρθωση: κοιτάζουμε κάθετα την κλίμακα ή βάζουμε ένα καθρεφτάκι και φροντίζουμε να συμπίπτει η βελόνα με το είδωλό της.)
Στη συνέχεια, θα δούμε τις δύο κατηγορίες σφαλμάτων που συναντάμε κάθε φορά που κάνουμε μια πειραματική μέτρηση. Ειδική αναφορά θα γίνει στα συστηματικά σφάλματα κατά την ανάγνωση μιας κλίμακας οργάνου, αναλογικού και ψηφιακού.

  • Συστηματικά σφάλματα

Είναι τα σφάλματα που δημιουργούν διαφορές μεταξύ της μέτρησης που κάνουμε και της αληθινής τιμής. Επηρεάζουν την ακρίβεια (accuracy) (Johnson, 1994) της μέτρησης, έννοια που σχολιάζεται στο Παράρτημα Β΄ του παρόντος βιβλίου. Τα συστηματικά σφάλματα:
  • Μπορεί να είναι σταθερά, οπότε επηρεάζουν κατά τον ίδιο τρόπο κάθε επόμενη μέτρηση.
    π.χ. Λάθος βαθμονόμησης οργάνων, μία τσίχλα κάτω από τη ζυγαριά, μετάθεση του μηδενός στο όργανο, ηθελημένη απλούστευση θεωρίας σχετικής με το πείραμα.
  • Μπορεί να αλλάζουν κατά τη διάρκεια του πειράματος.
    π.χ. Η ειδική θερμότητα του υλικού.
Η βελτίωση των συστηματικών σφαλμάτων απαιτεί εμπειρία και καλή γνώση της λειτουργίας κάθε οργάνου. Στο εκπαιδευτικό εργαστήριο η βελτίωσή τους επαφίεται στο προσωπικό. Στα δικά μας πειράματα τα συστηματικά σφάλματα θα τα θεωρούμε αμετάβλητα.

  • Τυχαία ή στατιστικά σφάλματα

Υποθέτουμε ότι τα ακούσια λάθη και τα συστηματικά σφάλματα έχουν, κατά το δυνατόν, βελτιωθεί και αρχίζεις να κάνεις τις μετρήσεις του μεγέθους με σκοπό τον προσδιορισμό της παραδεκτής/αληθινής τιμής του. Παρατηρείς ότι οι μετρήσεις -οι περισσότερες- διαφέρουν μεταξύ τους. Τα σφάλματα αυτά δεν μπορείς να τα αποδώσεις σε κάποια συγκεκριμένη αιτία. Δεν είναι τα ίδια κάθε φορά, είναι τυχαία.
Οφείλονται σε πολλούς λόγους, όπως:
  • στην ευαισθησία που διαθέτουν τα όργανα για την παρακολούθηση των μεταβολών που συμβαίνουν στο πείραμα,
  • σε ένα φαινόμενο που λέγεται ηλεκτρονικός θόρυβος (το οποίο δεν είναι θέμα του παρόντος βιβλίου).
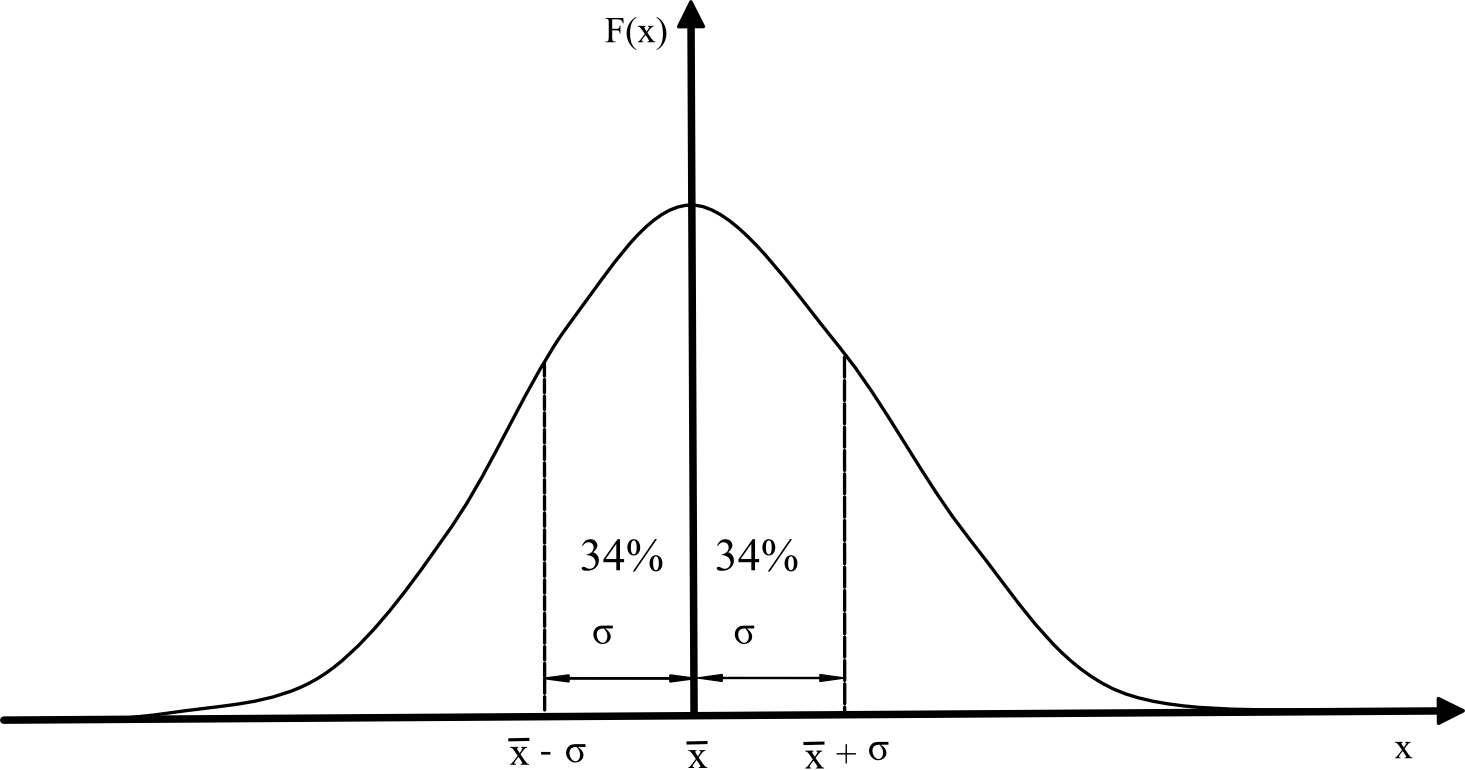
Στο σημείο αυτό θα δανειστούμε λίγες χρήσιμες γνώσεις από τη στατιστική θεωρία. Αυτή θα μας δώσει έναν τύπο που προσδιορίζει το εύρος μιας περιοχής τιμών μέσα στην οποία υπάρχει η αληθινή τιμή με συγκεκριμένη πιθανότητα. Σύμφωνα με τη συγκεκριμένη θεωρία, όταν κάνεις Ν ανεξάρτητες μετρήσεις, οι τιμές ακολουθούν μια κατανομή που περιγράφεται από μια συνάρτηση F(x) την οποία ονομάζουμε συνάρτηση κατανομής Gauss. Υποθέτουμε ότι οι μετρήσεις παρουσιάζουν μόνο τυχαία σφάλματα και ότι τα συστηματικά σφάλματα δεν καλύπτουν τα τυχαία. Αν ορίσουμε το \(\overline{x}=\frac{x_{1}+x_{2}+x_{3}+...+x_{N}}{N}\),τότε η γραφική παράσταση της F(x) είναι η Εικόνα Εισ.1.
Χωρίς απόδειξη, αναφέρουμε ότι στη γραφική παράσταση:
  1. Το γινόμενο F(x) dx δίνει την πιθανότητα να βρίσκεται η μέτρηση μέσα στο διάστημα x και x+dx.
  2. Το ολοκλήρωμα στο πεδίο τιμών του x δίνει πιθανότητα 1, δηλαδή η αληθινή τιμή υπάρχει στο πεδίο ορισμού με πιθανότητα 100%.
  3. Το ολοκλήρωμα της F(x) με όρια \(s=\pm \sqrt{\frac{\sum_{i=1}^{N}(x_{1}-\overline{x})^2}{N-1}}\)δίνει μια περιοχή στην οποία υπάρχει η αληθινή τιμή με πιθανότητα 68%. Το s λέγεται Τυπική Απόκλιση (ΤΑ). Στη διεθνή βιβλιογραφία η ΤΑ συμβολίζεται είτε με το σ (σίγμα) είτε με το αγγλικό s από τον όρο standard deviation (Taylor, 1997).
Αν, αντί για Ν μετρήσεις μία (1) φορά, κάνεις Ν μετρήσεις Ν φορές, το Μέσο Σφάλμα της Μέσης Τιμής (ΜΣΜΤ) ορίζει περιοχή με μικρότερο εύρος, αλλά με την ίδια πιθανότητα 68%, και δίνεται από τον τύπο: \[\sigma =\pm \sqrt{\frac{\sum_{i=1}^{N}(x_{1}-\overline{x})^2}{N\cdot (N-1)}}\]
(Εισ.1)
Παρατήρηση:
Στη βιβλιογραφία το ΜΣΜΤ συμβολίζεται με το \(\sigma _{\overline{x}}\)
Για λόγους γραμματοσειράς εμείς θα συμβολίζουμε το ΜΣΜΤ με το σ (σίγμα).

Εικόνα Εισ.1 Κατανομή Gauss

Στον Πίνακα Εισ.1 βλέπουμε τις πιθανότητες που αντιστοιχούν σε περιοχές της κανονικής κατανομής.
\(\overline{x}\pm \sigma \)  68%
\(\overline{x}\pm 2\sigma \)  95,5%
\(\overline{x}\pm 3\sigma \)  99,7%
\(\overline{x}\pm 5\sigma \)  99,99%

Πίνακας Εισ.1 Πιθανότητες και σ.


  • Σφάλμα ανάγνωσης κλίμακας οργάνου

Στο εργαστήριο Φυσικής υπάρχουν ψηφιακά και αναλογικά όργανα. Η ανάγνωση της κλίμακας και των δύο παρουσιάζει κάποια αβεβαιότητα που θα την ονομάζουμε σφάλμα ανάγνωσης. Η εκτίμηση αυτού του σφάλματος σε συνδυασμό με την ακρίβεια του οργάνου επηρεάζουν την ακρίβεια ενός πειράματος. Κάθε όργανο έχει τη δική του ακρίβεια η οποία εξαρτάται από την κατασκευή του, και είναι συνήθως γραμμένη σε κάποιο σημείο του οργάνου. Το σφάλμα ανάγνωσης το εκτιμά ο παρατηρητής ανάλογα με κάθε όργανο. Συνοπτικά, μπορούμε να πούμε ότι το σφάλμα ανάγνωσης του οργάνου προκύπτει από δύο παράγοντες: α) τον παρατηρητή, β) το συγκεκριμένο όργανο.

Σφάλμα ανάγνωσης σε αναλογικό όργανο

Η ακρίβεια του οργάνου είναι η μικρότερη υποδιαίρεση της κλίμακας που φέρει το όργανο. Στην Εικόνα Εισ.2 η ακρίβεια είναι 1 Ν.

Εικόνα Εισ.2 Κλίμακα αναλογικού οργάνου.

Το σφάλμα ανάγνωσης το αποφασίζει ο παρατηρητής, και εξαρτάται από την κατασκευή της κλίμακας του οργάνου και την εμπειρία του παρατηρητή. Στην παραπάνω κλίμακα το σφάλμα μπορεί να είναι \( \pm\) 0,2 N, οπότε γράφεις (5,4 \(\pm \)0,2) N με περιοχή αβεβαιότητας (5,2–5,6) Ν (όχι καλή απάντηση), ή μπορείς να γράψεις \(\pm \)0,1 Ν με περιοχή αβεβαιότητας (5,3–5,5) Ν (καλύτερη απάντηση ως προς την προηγούμενη).
Νομίζουμε ότι δεν υπάρχουν γενικοί κανόνες υπολογισμού αυτού του σφάλματος. Απαιτείται εξάσκηση και πείρα. Συμβουλευτείτε τον καθηγητή του εργαστηρίου. Για όλους τους παραπάνω λόγους, το σφάλμα ανάγνωσης θεωρείται στατιστικό σφάλμα (σε περίπτωση πολλών μετρήσεων), ενώ η ακρίβεια του οργάνου θεωρείται συστηματικό σφάλμα.

Σφάλμα ανάγνωσης σε ψηφιακό όργανο

Υποθέτουμε ότι η ένδειξη του οργάνου παραμένει σταθερή, οπότε την καταχωρείς. Ως σφάλμα ανάγνωσης αυτής της μέτρησης θεωρείς ότι είναι το μισό (1/2) της μικρότερης μεταβολής που μπορεί να κάνει το τελευταίο ψηφίο της κλίμακας.

Παράδειγμα:
Αν διαβάζεις 1,22 s, τότε υποθέτεις (ή ελέγχεις αν μπορείς) ότι η μικρότερη μεταβολή είναι \(\pm \)0,01s. Άρα, λαμβάνεις ως σφάλμα της ανάγνωσης το \(\pm \) 0,005s και γράφεις (1,220\(\pm \)0,005)s

Παρατήρηση: Ναι, έβαλες ένα ψηφίο το οποίο δε διάβασες στη μέτρηση, γιατί το σφάλμα του οργάνου υπαγορεύει την ακρίβεια. Στον ψηφιακό παλμογράφο η μικρότερη υποδιαίρεση αλλάζει ανάλογα και με την κλίμακα ανά υποδιαίρεση.

Περίπτωση: Όταν η ένδειξη του οργάνου δεν παραμένει σταθερή, αλλά αλλάζει μόνο το τελευταίο ψηφίο, τότε θεωρείς το σφάλμα στατιστικό. Παίρνεις μερικές ενδείξεις από αυτές που δείχνει το όργανο και υπολογίζεις τη μέση τιμή τους. Ως μέτρηση θεωρείς τη μέση τιμή αυτών των ενδείξεων, και την καταχωρείς.


Σημαντικά Ψηφία (ΣΨ)

Γενικά μιλώντας, όλοι οι αριθμοί έχουν τη δική τους σημασία χωρίς να υπάρχουν ανάμεσά τους σημαντικοί και ασήμαντοι. Στις Φυσικές Επιστήμες, όμως, οι αριθμοί που αναφέρονται σε μια μέτρηση προκύπτουν από τη συνεργασία οργάνου και ανθρώπου κατά τη διαδικασία αυτής της μέτρησης.
Γνωρίζουμε ότι κάθε πειραματική μέτρηση έχει μια αβεβαιότητα/σφάλμα που προκύπτει από το ίδιο το όργανο και τον άνθρωπο. Η αβεβαιότητα αυτή εκφράζεται με το πλήθος των ψηφίων τα οποία χρησιμοποιούμε στην απάντηση αυτή. Μπορούμε να συμφωνήσουμε ότι το πλήθος των ΣΨ του αριθμού της απάντησης εκφράζει το μέτρο της ακρίβειας της πειραματικής μέτρησης.

Κάθε πειραματική αβεβαιότητα/σφάλμα θα γράφεται με ένα ΣΨ, μη μηδενικό

Σημείωση:
Η ακρίβεια του οργάνου είναι δεδομένη και καθορίζεται από τον κατασκευαστή. Η ακρίβεια της μέτρησης εκφράζεται από το σχετικό σφάλμα της μέτρησης (βλ. Εισαγωγή, Σχετικό Σφάλμα μέτρησης), και είναι συνδυαστικό αποτέλεσμα οργάνου και παρατηρητή.

  • Κανόνες καθορισμού των ΣΨ μιας μέτρησης

  1. Για αριθμούς μικρότερους της μονάδας τα μηδενικά που είναι αριστερά από το πρώτο μη μηδενικό ψηφίο δεν λογαριάζονται ως ΣΨ.
    π.χ.: 0,03= 3∙10-3 → 1 ΣΨ
  2. . Για ακέραιους αριθμούς ως τελευταίο ΣΨ λαμβάνεται το δεξιότερο μη μηδενικό ψηφίο, δηλαδή δεν λαμβάνεις υπόψη σου τα μηδενικά που ακολουθούν.
    π.χ.: 1940 → 3 ΣΨ
  3. Για οποιοδήποτε αριθμό αποφασίζεις πόσα ΣΨ πρέπει να έχει, τον γράφεις ως δεκαδικό με τα ΣΨ που θέλεις, πολλαπλασιασμένο με την αντίστοιχη δύναμη του 10.
    π.χ.: 973, (1,33∙10-6), (0,000373= 3,73∙10-4), (0,955=9,55∙10-1), 7,55 → 3 ΣΨ
  4. Με καλή γνώση του φορητού υπολογιστικού μηχανήματος (scientific calculator) που όλοι διαθέτετε, ο αριθμός των ΣΨ καθορίζεται πολύ εύκολα (αρκεί να έχεις αποφασίσει πόσα ΣΨ πρέπει να έχει η μέτρηση).
    π.χ.: 49700=4,97∙104→ 3 ΣΨ
            49700= 4,970∙104 → 4 ΣΨ
Συνοψίζοντας, τα ΣΨ είναι ο αριθμός των ψηφίων μιας μέτρησης που γνωρίζουμε με απόλυτη βεβαιότητα.

  • Σημαντικά ψηφία και στρογγυλοποίηση

Όταν γράφεις το αποτέλεσμα μιας μέτρησης στο εργαστήριο Φυσικής, υπάρχουν τουλάχιστον δύο περιπτώσεις:
  • Ο αριθμός που γράφεις να εκφράζει το αποτέλεσμα μιας μέτρησης που έκανες με όργανο του εργαστηρίου.
  • Ο αριθμός αυτός να έχει προκύψει έπειτα από μαθηματικούς υπολογισμούς που έκανες χρησιμοποιώντας τα αποτελέσματα των μετρήσεων.
Είναι πιθανόν τα αποτελέσματα που προκύπτουν από μαθηματικούς υπολογισμούς να έχουν μεγαλύτερο πλήθος ΣΨ από αυτά που εκφράζουν τις πειραματικές συνθήκες (δηλαδή τα όργανα και τον παρατηρητή). Πρέπει λοιπόν να στρογγυλοποιήσεις τους αριθμούς αυτούς.

Βήμα 1ο: Στρογγυλοποιείς το σφάλμα και κρατάς ένα ΣΨ (εκτός αν αυτό είναι το 1 ή το 2, οπότε κρατάς δύο ΣΨ).

Βήμα 2ο: Παίρνεις τη μέση τιμή των μετρήσεων και την στρογγυλοποιείς, έτσι ώστε το τελευταίο ψηφίο της να είναι της ίδιας τάξης μεγέθους με το σφάλμα.

Παράδειγμα:
Αν δx=0,01 mm, τότε \(\mathrm{\overline{x}}\)=4,57 mm, οπότε γράφεις x\(\pm \) δx = (4,57\(\pm \)0,01) mm.
    Κατά τη στρογγυλοποίηση:
  • Αν θέλεις να διώξεις έναν από τους αριθμούς 1, 2, 3, 4, τότε το προηγούμενο ψηφίο παραμένει ως έχει.
  • Αν ο αριθμός που πρέπει να φύγει είναι ένας από τους 6, 7, 8, 9, τότε το προηγούμενο ψηφίο αυξάνεται κατά μία μονάδα.
  • Αν ο αριθμός αυτός είναι το 5, τότε κάνεις ή την πρώτη ή τη δεύτερη κίνηση (υπάρχει στατιστική ισορροπία).

Σχετικό σφάλμα μέτρησης
Όπως είδαμε, όταν γράφουμε την απάντηση x\(\pm \)δx, το Απόλυτο Σφάλμα δx μπορεί είτε να είναι το Μέγιστο Σφάλμα του οργάνου είτε να το υπολογίζεις με τύπο της στατιστικής (το σ). Και στις δύο περιπτώσεις το δx καθορίζει μια περιοχή, τις ιδιότητες της οποίας έχουμε ήδη αναφέρει.
Ένα άλλο σημαντικό μέγεθος είναι αυτό που ορίζεται από τη σχέση:\[\Sigma _{\sigma \chi }=\frac{\delta \mathrm{x}}{\mathrm{x}}100\%\]
(Εισ.2)

και ονομάζεται σχετικό σφάλμα της μέτρησης επί τοις % ή σχετική αβεβαιότητα της μέτρησης επί τοις %. Το μέγεθος αυτό ανάγει το σφάλμα στη μονάδα του μεγέθους και όχι στο μέτρο του μεγέθους, δηλαδή είναι ανεξάρτητο από το μέτρο του μεγέθους και γι’ αυτό το λόγο εκφράζει την ακρίβεια της μέτρησης. Το μέγεθος αυτό δεν έχει μονάδες, είναι ποσοστό.

Παράδειγμα:
Υπολογίζεις τη μάζα ενός σώματος με δύο τρόπους και βρίσκεις:
  • 1ος τρόπος: (40\(\pm \)1) kg με Σσχ= 2,5%.
  • 2ος τρόπος: (40\(\pm \)2) kg με Σσχ= 5%.
Συμπέρασμα: Ο πρώτος τρόπος είναι πιο ακριβής από τον δεύτερο.

pdf: Άμεσες μετρήσεις



Βίντεο: Άμεσες μετρήσεις


Βίντεο Εισ.1 Παρουσίαση των άμεσων μετρήσεων.



Μέτρηση ενός μεγέθους

  • Άμεση μέτρηση ενός μεγέθους

Στην άμεση μέτρηση, αφού επιλέξεις το κατάλληλο όργανο για το μέγεθος το οποίο θέλεις να μετρήσεις, κάνεις τη μέτρηση απευθείας με το όργανο και την καταχωρείς μαζί με τα αντίστοιχα σφάλματά της.

1η περίπτωση: Μία (1) μέτρηση
Αν κάνεις μία (1) μόνο μέτρηση, θα γράψεις το αποτέλεσμά σου x \(\pm \) δx, όπου:
x = το αποτέλεσμα της μέτρησης,
δx = το μέγιστο σφάλμα του οργάνου που χρησιμοποίησες.

Παράδειγμα:
Στην Εικόνα Εισ.3 το μέγιστο σφάλμα αυτού του οργάνου, σε μια πρώτη εκτίμηση, είναι δx=0,2°C.

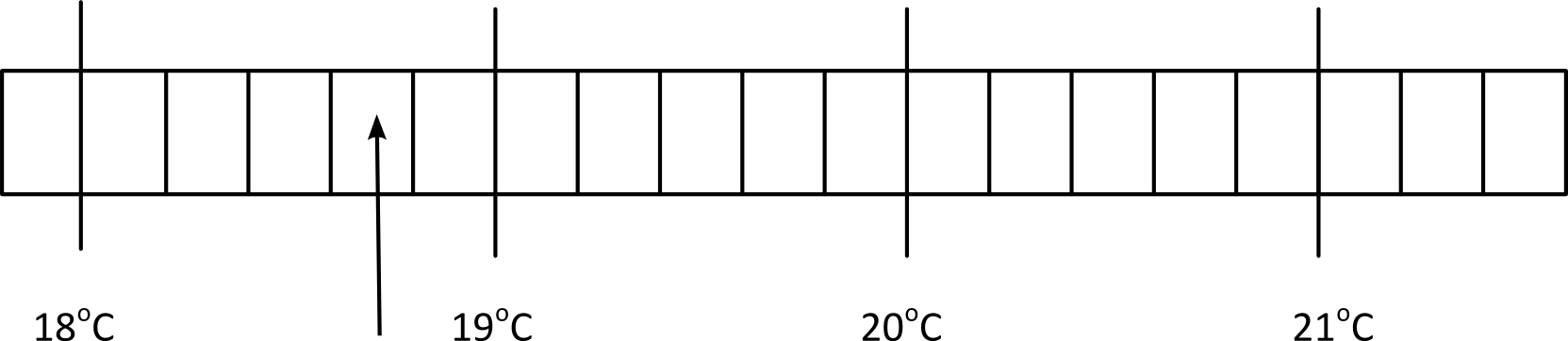
Εικόνα Εισ.3 Κλίμακα αναλογικού θερμομέτρου.

    Άρα, για τη μέτρηση που δείχνει το βέλος γράφεις (18,6 \(\pm \) 0,2) °C και δηλώνεις ότι:
  • Για σένα η θερμοκρασία είναι το x = 18,6°C.
  • Μέσα στο διάστημα 18,4–18,8°C είσαι 100% βέβαιος ότι υπάρχει και η αληθινή τιμή της θερμοκρασίας (αν δεν είναι 18,6°C).
  • Κάθε άλλη μέτρηση του ίδιου μεγέθους στις ίδιες συνθήκες πρέπει να περιέχεται μέσα στο διάστημα αυτό.
Εδώ πρέπει να πούμε ότι το μέγιστο σφάλμα του οργάνου μπορεί να εκτιμηθεί διαφορετικά από κάθε παρατηρητή. Αν εκτιμήσεις ότι το απόλυτο σφάλμα είναι δx = 0,1°C, η απάντηση θα είναι (18,6 \(\pm \) 0,1)°C. Άρα, η περιοχή αβεβαιότητας θα είναι από 18,5–18,7°C.

2η περίπτωση: Πολλές μετρήσεις
Αν μετρήσεις το ίδιο μέγεθος πολλές φορές και κάνεις Ν μετρήσεις, x1, x2, x3, ...., xN, τότε γράφεις το αποτέλεσμά σου με τη μορφή: \(\mathrm{\overline{x}}\)\(\pm \) δx, όπου το \(\mathrm{\overline{x}}\)είναι η μέση τιμή των μετρήσεων, δηλαδή \[\overline{X}=\frac{X_{1}+X_{2}+X_{3}+...+X_{N}}{N}\]
(Εισ.3)
    Αυτό για σένα σημαίνει ότι:
  • Έκανες Ν μετρήσεις, επειδή το έκρινες αναγκαίο.
  • Αυτή είναι η δική σου απάντηση για το μέγεθος.
  • Αυτή είναι για σένα η πιθανή τιμή.
  • Αυτή είναι για σένα η καλύτερη εκτίμηση για την αληθινή τιμή του μεγέθους.
  • Η αληθινή τιμή είναι μια εξιδανίκευση. Είναι αυτή που πλησιάζει την τιμή του μεγέθους μετά από πολλές μετρήσεις.
Το μέγεθος δx είναι το Απόλυτο Σφάλμα. Εμείς ως δx θα χρησιμοποιούμε το μέσο σφάλμα της μέσης τιμής (ΜΣΜΤ) των μετρήσεων που δίνεται από τη σχέση: \[\sigma_\overline{x} =\pm \sqrt{\frac{(x_{1}-\overline{x})^2+(x_{2}-\overline{x})^2+...+(x_{N}-\overline{x})^2}{N\cdot (N-1)}}\]
(Εισ.4)
Παρατήρηση: Για λόγους ευκολίας γραφής αντί για \(\sigma_\overline{x}\) θα γράφουμε σ.

Βίντεο: Μέση τιμή - Μέσο σφάλμα


Βίντεο Εισ.2 Υπολογισμός μέσης τιμής και μέσου σφάλματος με την αριθμομηχανή των Windows7.


Τι σημαίνει ο τρόπος γραφής \(\mathrm{\overline{x}}\)\(\pm \)σ ;
Απάντηση:
Σύμφωνα με τις μετρήσεις που έκανες, το \(\mathrm{\overline{x}}\) είναι η καλύτερη απάντηση για το μέγεθος που μέτρησες. Είναι η καλύτερη τιμή, σύμφωνα με τις δικές σου μετρήσεις. Με βάση την κατανομή Gauss, μέσα στην περιοχή \(\mathrm{\overline{x}-\sigma}\) έως \(\mathrm{\overline{x}+\sigma}\) βρίσκεται το 68% των μετρήσεων που έκανες. Αν κάνεις μια νέα μέτρηση, αυτή έχει πιθανότητα 68% να βρίσκεται μέσα στο συγκεκριμένο διάστημα. Παράλληλα, σημαίνει ότι υπάρχει πιθανότητα 68% η αληθινή τιμή να βρίσκεται στο ίδιο διάστημα. Στην περιοχή \(\mathrm{\overline{x}}\pm 2\sigma \) ισχύουν τα ίδια με πιθανότητα 95% (Taylor, 1997).
Παρατήρηση: Ο τύπος (Εισ.4) με τον οποίο υπολογίζουμε το ΜΣΜΤ έχει και αυτός πιθανότητα σφάλματος. Αυτή η πιθανότητα εξαρτάται από τον αριθμό Ν των μετρήσεων. Αυτό το σφάλμα του σφάλματος υπολογίζεται από τη σχέση: \[\pm\frac{\sigma_\overline{x}}{\sqrt{2\cdot (N-1)}}\]
    Παράδειγμα:
  • για Ν=10 το σφάλμα του είναι 24%
  • για Ν=50 το σφάλμα του \(\sigma_\overline{x}\) είναι 10%
  • για Ν=300 το σφάλμα του \(\sigma_\overline{x}\) είναι 4%
  • για Ν=1000 το σφάλμα του \(\sigma_\overline{x}\) είναι 2%
Στα εκπαιδευτικά εργαστήρια το Ν είναι, συνήθως, Ν \(\leq \) 10, οπότε το σφάλμα στον υπολογισμό του \(\sigma_\overline{x}\) είναι σημαντικό. Γι αυτό, οι τελικές τιμές των σφαλμάτων πρέπει να δίνονται με ένα (1) σημαντικό ψηφίο.

  • Έμμεση μέτρηση ενός μεγέθους

Στην έμμεση μέτρηση ενός μεγέθους δεν μετράμε το μέγεθος απευθείας με κάποιο όργανο, αλλά το υπολογίζουμε με τη βοήθεια κάποιου μαθηματικού τύπου ο οποίος περιέχει μεγέθη που έχουμε ήδη μετρήσει.

Πώς γράφω το αποτέλεσμα σε μια έμμεση μέτρηση;
Απάντηση:
Με τη μορφή χ\(\pm \)δχ, όπου το χ θα βρεθεί από το μαθηματικό τύπο που περιγράφει το μέγεθος.

Για τον υπολογισμό του δχ θα διακρίνουμε περιπτώσεις ανάλογα με τον μαθηματικό τύπο από τον οποίο υπολογίζεις το μέγεθος. Οι πλέον συχνές περιπτώσεις που θα συναντήσεις στα πρώτα σου εργαστήρια είναι:
  1. Γινόμενο π.χ. \(V={\alpha}\cdot{\beta}\cdot\gamma\)

  2. Διαίρεση π.χ. \(V=\frac{\alpha}{\beta}\)

  3. Δύναμη π.χ. \(V={\alpha}^3\cdot{\beta}\)

  4. Άθροισμα – Διαφορά π.χ.\(V={\alpha}+{\beta}\)  ή  \(V={\alpha}-{\beta}\)
όπου οι μετρήσεις για τα α, β, γ έχουν δώσει τα αποτελέσματα \(\alpha \pm \delta \alpha \), \(\beta \pm \delta \beta\), \(\gamma\pm \delta \gamma\).
Ας δούμε λοιπόν τις περιπτώσεις:

Γινόμενο

Αν ένα μέγεθος V υπολογίζεται από τον τύπο \(V={\alpha}\cdot{\beta}\cdot\gamma\), τότε για να βρεις το V, πολλαπλασιάζεις τα μεγέθη α, β, γ. Για να βρεις το δV, εφαρμόζεις τον τύπο: \[\frac{\delta V}{V}=\frac{\delta\alpha }{\alpha}+\frac{\delta\beta }{\beta }+\frac{\delta\gamma }{\gamma }\]
(Εισ.5)

που λέει ότι το Μέγιστο Σχετικό Σφάλμα υπολογίζεται από το άθροισμα των σχετικών σφαλμάτων των μεγεθών α, β και γ.
Παράδειγμα:
Αν α=(7\(\pm \)1) mm, β=(12\(\pm \)1) mm, γ=(15\(\pm \)1) mm,
V=α∙β∙γ ⇒ V = 7∙12∙15 = 1260 mm3
και δV = 369 mm3
V\(\pm \)δV= (1260\(\pm \)369) mm3

Διαίρεση

Η διαίρεση είναι και αυτή γινόμενο, οπότε ισχύει πάλι ο ίδιος κανόνας. Αν \(V=\frac{\alpha}{\beta}\), τότε: \[\frac{\delta V}{V}=\frac{\delta\alpha }{\alpha}+\frac{\delta\beta }{\beta }\]
(Εισ.6)

δηλαδή και πάλι το Μέγιστο Σχετικό Σφάλμα υπολογίζεται από το άθροισμα των σχετικών σφαλμάτων των μεγεθών α, β.
Παράδειγμα:
α=(80\(\pm \)1)g, β=(20\(\pm \)1) cm
\[V=\frac{80g}{20cm}=4 \frac{g}{cm}\]

\(\frac{\delta V}{4}=\frac{1}{80}+\frac{1}{20}\),  \(\delta V=0,3\frac{g}{cm}\)


Απάντηση:
(4,0\(\pm \)0,3) \(\frac{g}{cm}\)  (το μέγεθος αυτό εκφράζει τη γραμμική πυκνότητα υλικού).

Δύναμη

Η δύναμη είναι επίσης γινόμενο: V=α3∙β ⇒\(V=\alpha \cdot \alpha \cdot \alpha \cdot \beta\).  Άρα, \[\frac{\delta V}{V}=3\cdot \frac{\delta\alpha }{\alpha}+\frac{\delta\beta }{\beta }\]
(Εισ.7)

Αποδεικνύεται ότι και για αρνητικούς εκθέτες το Μέγιστο Σχετικό Σφάλμα γράφεται χωρίς το πρόσημο πλην.
Παράδειγμα:
\[V=\alpha^{-3}\cdot\beta \Rightarrow \frac{\delta V}{V}=3\cdot \frac{\delta\alpha }{\alpha}+\frac{\delta\beta }{\beta }\]

Άθροισμα-Διαφορά

Αν V=α+β, τότε δV=δα+δβ.
Αν V=α-β, τότε δV=δα+δβ (πάλι).

Εδώ η θεωρία λέει ότι το Απόλυτο Μέγιστο Σφάλμα του έμμεσου μεγέθους ισούται με το άθροισμα των απόλυτων σφαλμάτων των α και β, δηλαδή δV=δα+ δβ (πάντα)
Παράδειγμα:
  1. Αν α=(62,8\(\pm \) 0,3) g, β=(15,4\(\pm \)0,2) g, τότε
    V=62,8+15,4=78,2 g
    δV=(0,3+0,2) g, δV=0,5 g
    Απάντηση: (78,2\(\pm \)0,5) g
  2. Αν V=α-β, τότε V=62,8-15,4=47,4 g
    δV=(0,3+0,2) g, δV=0,5 g
    Απάντηση: (47,4\(\pm \)0,5) g
Θα ανακεφαλαιώσουμε τις πρώτες γνώσεις για τη σημασία της σχετικής αβεβαιότητας με μια παλιά ερώτηση: αν τεντώσουμε μια αλυσίδα, σε ποιο σημείο θα σπάσει; Η απάντηση είναι: εκεί όπου υπάρχει ο πιο αδύναμος κρίκος. Με άλλα λόγια, πρέπει να βελτιώσεις την πιο ασθενή μέτρηση της διαδικασίας, δηλαδή αυτή με το μεγαλύτερο σχετικό σφάλμα, η οποία έχει και τη μεγαλύτερη συμμετοχή στον υπολογισμό της σχετικής αβεβαιότητας στο συγκεκριμένο πείραμα. Έτσι, η παρέμβαση αυτή θα γίνει αφορμή για ουσιαστικές σκέψεις πάνω στις αιτίες που συμβάλλουν στις αβεβαιότητες του πειράματος.
Παράδειγμα:
Για την πυκνότητα \[ρ=\frac{m}{V}\] ενός ομογενούς υλικού ισχύει: \[\frac{\delta\rho}{\rho}=\frac{\delta m}{m}+\frac{\delta V }{V}\] Όταν υπολογίσεις τις τιμές των κλασμάτων, θα μπορέσεις να αποφασίσεις με τι ποσοστό συμμετέχει το καθένα στη συνολική αβεβαιότητα, και να δεις πώς μπορείς να κάνεις βελτιώσεις όπου χρειάζεται.
Με τις σκέψεις αυτές ο υπολογισμός της σχετικής αβεβαιότητας αποκτά ένα πιο ουσιαστικό νόημα και δίνει άλλο ενδιαφέρον στις αλγεβρικές πράξεις που έκανες. Για την πρώτη επαφή με τα Σφάλματα θεωρούμε ότι είναι αρκετά μέχρι εδώ.
Για περίεργους και φιλομαθείς:
Αν θέλεις περισσότερα, βλ. Παράρτημα Α. Εκεί, με τη βοήθεια των Μερικών Παραγώγων, θα δεις τα γενικά θεωρήματα για Σύνθετες Συναρτήσεις. Είναι πιο εύκολο απ’ ό,τι φαντάζεσαι!

Τρόποι ελέγχου του αποτελέσματος

Για τον έλεγχο των αποτελεσμάτων θα χρησιμοποιήσουμε τρεις (3) τρόπους:

1ος τρόπος
Ένας απλός τρόπος για να ελέγξεις το αποτέλεσμά σου είναι να βρεις την επί τοις % διαφορά μεταξύ της αληθινής τιμής ΧA και της δικής σου πειραματικής τιμής ΧΠ: \[X=\frac{\left | X_{A}-X_{\Pi } \right |}{X_{A}}100\%\]
(Εισ.8)

Όλες οι πειραματικές διατάξεις του εργαστηρίου δίνουν αποτελέσματα κάτω από το 10%. Αυτό βέβαια δεν είναι κανόνας, γιατί πολλά μπορούν να συμβούν κατά την πορεία των μετρήσεών σου. Συζητάς το αποτέλεσμα με τους διδάσκοντες του εργαστηρίου.

2ος τρόπος
Γράφεις τη δική σου απάντηση (Χ\(\pm \)δx). Η αληθινή τιμή είναι (Υ\(\pm \)δy). Αν τα δύο διαστήματα έχουν επικάλυψη, τότε λες ότι το αποτέλεσμα είναι αποδεκτό μέσα στα όρια των σφαλμάτων της μέτρησης.
Παράδειγμα:
Για κάποια πυκνότητα βρήκες (7,3\(\pm \)0,2) g/cm3 , ενώ η θεωρητική τιμή είναι (7,6\(\pm \)0,2) g/cm3.
Τα δύο διαστήματα, όπως φαίνεται στην Εικόνα Εισ.4, έχουν επικάλυψη τιμών. Άρα, η απάντησή σου είναι αποδεκτή.

Εικόνα Εισ.4 Διάστημα τιμών.


3ος τρόπος
Με το σχετικό σφάλμα της μέτρησης \(\overline{\mathrm{x}}\pm\Sigma _{\sigma \chi }\), μεταξύ δύο μετρήσεων του ιδίου μεγέθους πιο ακριβής είναι αυτή που έχει το μικρότερο σχετικό σφάλμα (με την προϋπόθεση ότι γίνονται κάτω από τις ίδιες συνθήκες).

pdf: Έμμεσες μετρήσεις



Βίντεο: Έμμεσες μετρήσεις


Βίντεο Εισ.3 Παρουσίαση των έμμεσων μετρήσεων.



Γραφικές Παραστάσεις (ΓΠ)

Σήμερα υπάρχουν δύο τρόποι για τη γραφική αναπαράσταση ενός συνόλου δεδομένων:

1ος τρόπος
Με χάρακα, χαρτί, μολύβι, γνώση και προσπάθεια

2ος τρόπος
Με τον Η/Υ στον οποίο δίνεις μια φορά το σύνολο των δεδομένων και στη συνέχεια με ένα κλικ έχεις τη γραφική παράσταση. Προσοχή, διότι για τον τρόπο αυτό χρειάζονται οι γνώσεις που αποκτάς από την προηγούμενη περίπτωση, καθώς και επιπλέον γνώσεις σχετικές με το πρόγραμμα που χρησιμοποιείς.
Εμείς εδώ θα ασχοληθούμε με τον πρώτο τρόπο χάραξης ΓΠ. Συγκεκριμένα, θα μιλήσουμε για ΓΠ που παριστάνουν καμπύλες/ευθείες σε δύο διαστάσεις και καρτεσιανό επίπεδο (Εργαστηριακές Ασκήσεις Φυσικής, 2013). Δεν θα ασχοληθούμε με ιστογράμματα και πίτες (pies).
Ας δούμε τους λόγους για τους οποίους κάνουμε μια γραφική παράσταση:
  • 1ος λόγος
    Για να απεικονίσουμε δεδομένα με έναν τρόπο που μας δίνει πολλές πληροφορίες, εύκολα και με μια ματιά.
    π.χ. Το ποσοστό αύξησης των κερδών μιας τράπεζας κατά τους τελευταίους 12 μήνες. Εύκολα μπορείς να βγάλεις συμπεράσματα για την πορεία της επιχείρησης.
  • 2ος λόγος
    Κάνουμε τη γραφική παράσταση με σκοπό να αναλύσουμε ένα σύνολο πειραματικών δεδομένων και να βγάλουμε συμπεράσματα. Γι’ αυτό, στην περίπτωση αυτή η χάραξη πρέπει να γίνει με μεγαλύτερη αυστηρότητα. Βέβαια, τίποτα δεν αποκλείει να κάνεις τα ίδια και στην προηγούμενη περίπτωση, αλλά δεν είναι τόσο απαραίτητο.
Μια διαφορά:
  • Ο Μαθηματικός:
    • Γνωρίζει τη συνάρτηση που συνδέει την ανεξάρτητη μεταβλητή Χ με την εξαρτημένη Υ.
      π.χ.: Υ=αΧ+β, οπότε δίνει τυχαίες τιμές στο Χ, κάνει πράξεις και υπολογίζει το Υ
    • Γράφει το αποτέλεσμά του με όσα δεκαδικά νομίζει ότι του χρειάζονται και, τέλος, βάζει τα ζεύγη (Χ,Υ) σε άξονες.
    • Οπότε, όλα τα σημεία σχηματίζουν μια γνωστή καμπύλη (που ξέρει από τα μαθηματικά).

  • Ο Τεχνολόγος:
    • Έχει τα ζεύγη (Χ,Υ) που είναι αποτελέσματα μετρήσεων και περιέχουν τις γνωστές αβεβαιότητες (σφάλματα).
    • Ξέρει ότι κάθε ζεύγος δίνει και ένα σημείο στο επίπεδο.
    • Τι θέλει να κάνει με τα σημεία αυτά; Υπάρχουν δύο περιπτώσεις:
      • 1η περίπτωση:

        Να ερευνήσει αν οι τιμές των (Χ,Υ) ικανοποιούν κάποια σχέση που περιγράφει το πείραμα από το οποίο προέκυψαν αυτές οι τιμές. Με άλλα λόγια, κάνει επαλήθευση κάποιου Νόμου ή ψάχνει για το Νόμο.
      • 2η περίπτωση:

        Ξέρει από πριν την εξίσωση που περιγράφει το φαινόμενο. Άρα, ξέρει και τη μορφή της μαθηματικής καμπύλης που αντιστοιχεί στην εξίσωση.
    • Οπότε, με βάση τα πειραματικά σημεία που διαθέτει, θέλει να χαράξει την καλύτερη καμπύλη που πλησιάζει στη θεωρητική μαθηματική καμπύλη. Αυτή η καλύτερη καμπύλη (best fit) δίνει τώρα τις πληροφορίες για το πείραμα. Τα πειραματικά σημεία δεν παίζουν κανένα ρόλο πλέον. Δεν θα τα χρησιμοποιήσει για κανέναν υπολογισμό.

Τώρα μπαίνουν δύο ερωτήματα:
Ερώτημα 1ο: Πώς χαράζω την καλύτερη πειραματική καμπύλη;
Απάντηση:
Για να χαράξεις την καλύτερη πειραματική καμπύλη, πρέπει να βάλεις τα σημεία (Χ,Υ) σε ένα επίπεδο με άξονες Χ και Υ. Για να το κάνεις αυτό, πρέπει να βαθμονομήσεις τους άξονες. Σύμφωνα με το πεδίο τιμών των Χ και Υ, αποφασίζεις πόσες γραμμές θέλεις να αντιστοιχίσεις, έτσι ώστε να καλύψεις το μεγαλύτερο δυνατό χώρο σε όλο το επίπεδο. Υπάρχει λόγος γι αυτό τον οποίο θα δούμε παρακάτω. (Ούτε γραφική παράσταση σαν κυπαρισσάκι ούτε πατημένη από τρένο, όπως φαίνεται στην Εικόνα Εισ.5.)

  

Εικόνα Εισ.5 Λανθασμένες γραφικές παραστάσεις.

Παράδειγμα:
Σε 10 μικρές γραμμές του μιλιμετρέ δεν αντιστοιχείς 12 cm, αλλά 5 cm, 10 cm ή 20 cm, έτσι ώστε να ξέρεις εύκολα σε τι αντιστοιχεί μία γραμμή του άξονα.
Περίπτωση 1η:
Μία (1) γραμμή του άξονα Χ αντιστοιχεί σε 2 cm.
Στο κάτω μέρος του μιλιμετρέ γράψε την αντιστοίχιση που αποφάσισες.
Περίπτωση 2η:
Στον Χ άξονα: μία (1) γραμμή 2 cm.
Στον Υ άξονα: μία (1) γραμμή 0,1 Ν.

Πάνω στους άξονες γράφεις μόνο τις τιμές της βαθμονόμησης και τις μονάδες. Δεν γράφεις πειραματικές τιμές. Μετά τη βαθμονόμηση βάζεις τα σημεία που αντιστοιχούν στα πειραματικά ζεύγη (Χ,Υ) με ή χωρίς τα διαστήματα εμπιστοσύνης (error bars). Αν y\(\pm \)σ, τότε το διάστημα εμπιστοσύνης είναι ένα ευθύγραμμο τμήμα μήκους 2σ, κάθετο στον άξονα Χ, με κέντρο το σημείο (Χ,Υ).
Τώρα έχεις βάλει τα πειραματικά σημεία και πρέπει να χαράξεις την πειραματική καμπύλη. Αυτό μπορεί να γίνει με τρεις (3) τρόπους:

1ος τρόπος
Χαράζεις την καμπύλη/ευθεία έτσι, ώστε όσα σημεία αφήνει έξω από τη μία μεριά, τόσα να αφήνει και από την άλλη σε ισαπέχουσες θέσεις. Η χάραξη γίνεται με χάρακα για ευθεία ή καμπυλόγραμμο για υπερβολές, παραβολές κτλ.
2ος τρόπος
Χαράζεις την καμπύλη έτσι, ώστε να περνάει μέσα από όλα τα διαστήματα εμπιστοσύνης (error bars). Αυτός ο τρόπος θεωρείται καλύτερος από τον πρώτο.
3ος τρόπος
Δίνεις τα ζεύγη (Χ,Υ) στον Η/Υ. Αυτός βάζει τα σημεία και σχεδιάζει την καλύτερη δυνατή καμπύλη. Επιπλέον, σου δίνει και την μαθηματική εξίσωση της καλύτερης καμπύλης που αντιστοιχεί στα πειραματικά σημεία.

Ερώτημα 2ο: Τι πληροφορίες μπορώ να πάρω από την καλύτερη πειραματική καμπύλη;
Απάντηση:
Ανάλυση δεδομένων:
  • Βρίσκεις για κάθε τιμή xν την αντίστοιχη τιμή yν, και αντίστροφα
  • Βρίσκεις την τιμή ενός τρίτου μεγέθους (εκτός των xν, yν) που ονομάζουμε κλίση λ και ορίζεται από τη σχέση:
\[\lambda =\frac{dy}{dx}\]
(Εισ.9)

Πώς βρίσκω την κλίση λ από τη γραφική παράσταση;

pdf: ΓΠ στο μιλιμετρέ



Βίντεο: ΓΠ στο μιλιμετρέ


Βίντεο Εισ.4 Γραφικές παραστάσεις στο μιλιμετρέ.

1η περίπτωση
Αν η γραφική παράσταση είναι ευθεία, σχηματίζεις ένα τυχαίο, μεγάλο τρίγωνο με υποτείνουσα πάνω στην ευθεία. Διαιρείς την κατακόρυφη πλευρά του τριγώνου Δy με την οριζόντια πλευρά Δx. \[\lambda =\frac{\Delta y}{\Delta x}\] Δεν χρησιμοποιείς πειραματικά σημεία για να βρεις την κλίση.

2η περίπτωση
Αν η γραφική παράσταση είναι καμπύλη, τότε φέρνεις την εφαπτομένη στο σημείο M1 που σε ενδιαφέρει, σχηματίζεις πάλι ένα μεγάλο τρίγωνο και υπολογίζεις την κλίση (Εικόνα Εισ.6).
π.χ. \[\lambda =\frac{\Delta y}{\Delta x}=\frac{\mathrm{AB}}{\Gamma {\mathrm{B}}}\]

Εικόνα Εισ.6 Κλίση σε ένα σημείο της καμπύλης.

Προσοχή: Η κλίση έχει μονάδες, τις μονάδες των αξόνων

Θεώρημα:
Έστω, y=f(x) η εξίσωση μιας καμπύλης και έστω, Μ1(x1,y1) ένα σημείο πάνω στην καμπύλη αυτή. Η κλίση στο σημείο αυτό είναι ίση με την τιμή της πρώτης παραγώγου. \[{f}'(x)=\frac{dy}{dx}\]
(Εισ.10)


Πώς βρίσκω την κλίση λ γνωρίζοντας την εξίσωση της γραφικής παράστασης;

Βίντεο: ΓΠ στο Excel


Βίντεο Εισ.5 Γραφικές παραστάσεις στο Excel.

Eσύ vs Η/Υ
Έχεις δώσει τα ζεύγη (x,y) στον Η/Υ και έχεις πάρει την καλύτερη καμπύλη και την εξίσωση που της αντιστοιχεί. Βρίσκεις την παράγωγο και, στη συνέχεια, την αριθμητική τιμή της παραγώγου για το x που σε ενδιαφέρει. Από το θεώρημα ξέρεις ότι η τιμή της παραγώγου είναι η ζητούμενη κλίση. Κάνεις σύγκριση. Γιατί μεγάλο τρίγωνο;

y1\(\pm \)δy1, y2\(\pm \)δy2, x1\(\pm \)δx1, x2\(\pm \)δx2
Δy= y2 - y1, δ(Δy)= δy1+ δy2
Δx= x2 - x1, δ(Δx)= δx2+ δx1 \[\lambda =\frac{\Delta y}{\Delta x}\] άρα   \[\frac{\delta \lambda }{\lambda }=\frac{\delta (\Delta y)}{\Delta y}+\frac{\delta (\Delta x)}{\Delta x}\]

Συμπέρασμα: μεγάλα Δx, Δy, μικρό δλ!


Μέθοδος Ελαχίστων Τετραγώνων
1ος τρόπος
Αν έχεις κάνει Ν μετρήσεις και έχεις τοποθετήσει τα σημεία στο Χ,Υ επίπεδο, τότε ένας πολύ σωστός τρόπος για να φέρεις την καλύτερη ευθεία που αντιστοιχεί στα σημεία αυτά είναι να υπολογίσεις την κλίση της ευθείας και το σημείο που τέμνει τον άξονα Υ. Δηλαδή, αν Υ=ΑΧ+Β, αποδεικνύεται ότι το Α και το Β υπολογίζονται ως εξής: \[A=\frac{N\sum X_{i}\cdot Y_{i}-\sum X_{i}\cdot \sum Y_{i} }{\Gamma }\]
(Εισ.11)

\[B=\frac{\sum X_{i}^2\cdot \sum Y_{i}-\sum X_{i}\cdot\sum X_{i}\cdot Y_{i} }{\Gamma }\]
(Εισ.12)

\[\Gamma =N\sum X_{i}^2-(\sum X_{i})^2\]
(Εισ.13)

Σημείωση:
Δε νομίζουμε ότι κάποιος θα κάνει ποτέ αυτές τις πράξεις στο εργαστήριο. Είναι χρήσιμο, όμως, να ξέρεις ότι υπάρχει αυτή η μέθοδος.


2ος τρόπος
Δίνεις τα Ν ζεύγη (Χ,Υ) στον Η/Υ ή στο φορητό υπολογιστικό μηχάνημά σου (scientific calculator), και σε απειροστό χρόνο σου δίνουν τα Α και Β! Η ίδια μέθοδος για τα μεγέθη Α και Β υπολογίζει και τις αβεβαιότητες δΑ και δΒ, αλλά δε θα χρειαστούν στο εισαγωγικό εργαστήριο. Τώρα που ξέρεις τα Α και Β, γνωρίζεις την εξίσωση.
Παράδειγμα:

y=2,6x +3,2

(Εισ.14)

Για να χαράξεις την ευθεία, χρειάζονται δύο σημεία (το είπε και ο Ευκλείδης), όχι βέβαια τα πειραματικά. Δίνεις δύο τιμές στον Χ και από την εξίσωση (Εισ.14) έχεις δύο τιμές του Υ. Με τα δύο σημεία (Χ1,Υ1) και (Χ2, Υ2) χαράζεις την καλύτερη ευθεία. Τέλος!
Παράδειγμα υπολογισμού των Α και Β

Πίνακας Εισ.2 Παράδειγμα υπολογισμού των Α και Β.

\[A=\frac{5\cdot 180,14-16,0\cdot 48,5 }{52,1}=2,39\] \[B=\frac{61,62\cdot 48,5-16,0\cdot 180,14 }{52,1}=2,04\]

Γ=5∙61,62-(16,0)2 =52,1
y=2,39x+2,04



ΚΡΙΤΗΡΙA ΑΞΙΟΛΟΓΗΣΗΣ

  • Κριτήριο αξιολόγησης 1 - Άμεσες Μετρήσεις

    Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος
    1. Το σχετικό σφάλμα εκφράζει την ακρίβεια της μέτρησης.
      2. Σωστό Σωστή επιλογή. Λάθος Λάθος επιλογή.
    2. Ο τρόπος γραφής των αποτελεσμάτων των μετρήσεων (σύμφωνα με τη Θεωρία Σφαλμάτων) είναι: x – δx
      3. Σωστό Λάθος επιλογή. Το σωστό είναι x\(\pm \)δx. Λάθος Σωστή επιλογή. Το σωστό είναι x\(\pm \)δx.
    3. Το απόλυτο σφάλμα δεν έχει μονάδες, είναι καθαρός αριθμός.
      4. Σωστό Λάθος επιλογή. Έχει μονάδες, αυτές του μεγέθους που μετρώ. Λάθος Σωστή επιλογή. Έχει μονάδες, αυτές του μεγέθους που μετρώ.
    4. Το Μέσο Σφάλμα της Μέσης Τιμής (ΜΣΜΤ) δεν έχει μονάδες, είναι καθαρός αριθμός.
      5. Σωστό Λάθος επιλογή. Έχει μονάδες, αυτές του μεγέθους που μετρώ. Λάθος Σωστή επιλογή. Έχει μονάδες, αυτές του μεγέθους που μετρώ.
    5. Η μέτρηση Ι=2,3\(\pm \)0,1 Α είναι σωστή.
      6. Σωστό Λάθος επιλογή. Το σωστό είναι: Ι=(2,3\(\pm \)0,1)Α. Λάθος Σωστή επιλογή. Το σωστό είναι: Ι=(2,3\(\pm \)0,1)Α.
    6. Στις πολλές μετρήσεις το σφάλμα είναι η μέση τιμή των σφαλμάτων των μετρήσεων.
      7. Σωστό Λάθος επιλογή. Είναι το Μέσο Σφάλμα της Μέσης Τιμής. Λάθος Σωστή επιλογή. Είναι το Μέσο Σφάλμα της Μέσης Τιμής.
    7. Το σχετικό σφάλμα έχει τις ίδιες μονάδες με το μέγεθος που μετρώ.
      8. Σωστό Λάθος επιλογή. Δεν έχει μονάδες. Λάθος Σωστή επιλογή. Δεν έχει μονάδες.
    8. Μεταξύ δύο μετρήσεων πιο ακριβής είναι αυτή που έχει το μικρότερο απόλυτο σφάλμα.
      9. Σωστό Λάθος επιλογή. Είναι αυτή που έχει το μικρότερο σχετικό σφάλμα. Λάθος Σωστή επιλογή. Είναι αυτή που έχει το μικρότερο σχετικό σφάλμα.
    9. Το σχετικό σφάλμα της μέτρησης (20\(\pm \)2) mm είναι 0,1 mm
      10. Σωστό Λάθος επιλογή. Το σχετικό σφάλμα δεν έχει μονάδες. Λάθος Σωστή επιλογή. Το σωστό είναι 0,1. Το σχετικό σφάλμα δεν έχει μονάδες.
    10. Το επί τοις % σχετικό σφάλμα της μέτρησης (20\(\pm \)2) mm είναι 10%.
      11. Σωστό Σωστή επιλογή. Λάθος Λάθος επιλογή.
    11. Η μέτρηση της θερμοκρασίας με ένα θερμόμετρο είναι άμεση μέτρηση.
      12. Σωστό Σωστή επιλογή. Λάθος Λάθος επιλογή.
    12. Μετράς ένα μέγεθος τρεις (3) φορές και βρίσκεις 2,3 cm την πρώτη φορά, 2,4 cm τη δεύτερη και 2,5 cm την τρίτη. Το αποτέλεσμα της μέτρησης είναι 2,4 cm.
      13. Σωστό Σωστή επιλογή. Λάθος Λάθος επιλογή.
    13. Μετράς ένα μέγεθος μία (1) φορά. Το σφάλμα είναι το μέγιστο σφάλμα του οργάνου.
      14. Σωστό Σωστή επιλογή. Λάθος Λάθος επιλογή.
    14. Μετράς ένα μέγεθος 5 φορές. Το αποτέλεσμα της μέτρησης είναι η μέση τιμή των 5 μετρήσεων.
      15. Σωστό Σωστή επιλογή. Λάθος Λάθος επιλογή.
    15. Μετράς ένα μέγεθος πολλές φορές. Το σφάλμα της μέτρησης είναι το Μέσο Σφάλμα της Μέσης Τιμής (ΜΣΜΤ).
      16. Σωστό Σωστή επιλογή. Λάθος Λάθος επιλογή.

  • Κριτήριο αξιολόγησης 2 - Έμμεσες μετρήσεις

  1. Γνωρίζοντας ότι:
    a=2S/t2

    (S\(\pm \)δS): (100\(\pm \)1) cm

    (t\(\pm \)δt):(10,5\(\pm \)0,1) s

    να βρείτε το (a\(\pm \)δa).

    2. Απάντηση

    \[a=\frac{2S}{t^{2}}=\frac{2\cdot 100cm}{(10,5s)^{2}}=1,814059\frac{cm}{s^2}\]

    Άρα, (a\(\pm \) δa): (1,81\(\pm \)0,05) cm/s2


  2. Γνωρίζοντας ότι:
    Δθ=θ2 - θ1

    (θ2 \(\pm \)δθ2): (100 \(\pm \)1)°C

    (θ1 \(\pm \)δθ1): (90\(\pm \)1)°C

    να βρείτε το (Δθ\(\pm \)δΔθ).

    3. Απάντηση

    Δθ=θ2 – θ1 =100 °C - 90 °C=10 °C
    δΔθ=δθ1+δθ2=1 °C +1 °C=2 °C
    Άρα, (Δθ\(\pm \)δΔθ): (10\(\pm \)2) °C.


  3. Αν η πειραματική τιμή ενός μεγέθους είναι 51,0 cm και η αληθινή 50,0 cm, βρείτε τη διαφορά επί τοις % ως προς την αληθινή τιμή.

    4. Απάντηση



  • Κριτήριο αξιολόγησης 3 - Γραφικές Παραστάσεις

    Ερωτήσεις:
  1. Στην 1η γραφική παράσταση φαίνεται το διάστημα που διανύει ένα σώμα σε σχέση με το χρόνο.
    1. Να βρεθεί η κλίση της ευθείας.
    2. Πόσο διάστημα έχει διανύσει το σώμα σε 20 s;
    3. Πόσο χρόνο χρειάζεται για να διανύσει 130 m;

    Απάντηση

    1. Παίρνω δύο σημεία Α,Β πάνω στην ευθεία, όπως φαίνεται στην (α). Φτιάχνω το ορθογώνιο τρίγωνο ΑΒΓ και διαιρώ την κατακόρυφη πλευρά ΑΓ προς την οριζόντια ΒΓ.

    2. Όπως βλέπω στην (β), στα 20 s το σώμα έχει διανύσει 52 m.
    3. Το σώμα για να διανύσει 130 m χρειάζεται 50 s.


  2. Στη 2η γραφική παράσταση να βρεθεί η κλίση της καμπύλης στη θέση V=1V με τη βοήθεια της εφαπτομένης που έχει χαραχθεί στη θέση αυτή.

    3. Απάντηση

    Παίρνω δύο σημεία Α,Β πάνω στην εφαπτομένη. Φτιάχνω το ορθογώνιο τρίγωνο ΑΒΓ και διαιρώ την κατακόρυφη πλευρά ΑΓ προς την οριζόντια ΒΓ.


  3. Στην 3η γραφική παράσταση να βρεθεί η κλίση της καμπύλης στη θέση t= 10 h με τη βοήθεια της εξίσωσής της.

    4. Απάντηση

    Παραγωγίζω την εξίσωση 26x2+13x+4 και έχω 52x+13. Αντικαθιστώ όπου x το 10, και έχω 533.
    Άρα, η κλίση είναι 533 m/h.

    Εικόνα Εισ.7 Ερώτηση Κριτηρίου Αξιολόγησης 3 – Γραφικές παραστάσεις.


    Βιβλιογραφία
    • Johnson, R. (1994). Miller and Freud’s Probability and Statistics for Engineers (σ. 25, 109, 143, 202 και 205). New Jersey: Prentice Hall.

    • Taylor, J. R. (1997). Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. (κεφάλαια 2, 3.3, 3.5, 4.1, 4.2, 4.3, 4.4, 5.3, 5.4 και 8). University Science Books.

    • Εργαστηριακές Ασκήσεις Φυσικής. τόμ.Ι. (2013). [Εργαστηριακός Οδηγός - Πανεπιστημιακές Σημειώσεις] Εθνικό Μετσόβιο Πολυτεχνείο, Τομέας Φυσικής, Σχολή Εφαρμοσμένων Μαθηματικών και Θετικών Επιστημών, Εκπαιδευτικά Εργαστήρια [online] διαθέσιμο από:
      <http://www.physics.ntua.gr/ergasthria/askhseis_ergasthrion/eo_tomos1_2013.pdf>

    • Καραμπαρμπούνης, Α. κ.ά. (2012). Εισαγωγή στην Πειραματική Μεθοδολογία. Στο Εισαγωγικές Διαλέξεις Εργαστηρίου Φυσικής 2014-2015 [Φυλλάδιο Εισαγωγικών Διαλέξεων - Πανεπιστημιακές Σημειώσεις], Εθνικό & Καποδιστριακό Παν/μιο Αθηνών, Τμήμα Φυσικής, Εργαστήριο Φυσικής [online] διαθέσιμο από:
      <http://physlab.phys.uoa.gr/f1/intro_lectures2012.pdf>