7.2 Αλγόριθμοι Monte Carlo

Ας δούμε ένα πολύ απλό παράδειγμα. Στόχος μας είναι ο υπολογισμός του αριθμού $\pi$ μέσω του παρακάτω μοντέλου – αλγορίθμου.

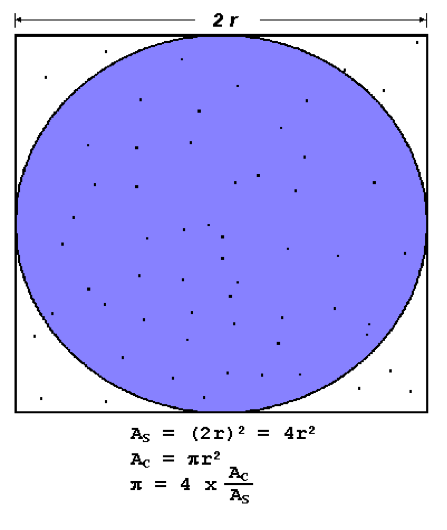
Το πείραμα σταγόνων βροχής (raindrop experiment): Έστω τετράγωνο το οποίο περικλείει ένα κύκλο. Η ακτίνα του κύκλου είναι r ενώ το μήκος κάθε πλευράς του τετραγώνου είναι ίσο με τη διάμετρο του κύκλου, $2r$ (Σχήμα 7.1). Το εμβαδόν του κύκλου είναι:

$$A_c=\pi r^2$$

(7.1)

ενώ το εμβαδόν του τετραγώνου με το οποίο τον περικλείουμε

$$A_s={(2r)}^2=4r^2.$$

(7.2)

Εύκολα βλέπουμε ότι ο αριθμός $\pi$ μπορεί να υπολογισθεί ως:

$$\pi =4\frac{A_c}{A_s}.$$

(7.3)

Για τον υπολογισμό λοιπόν του $\pi$ χρειαζόμαστε τον υπολογισμό του λόγου των δύο εμβαδών, $A_c/A_s$. Ο υπολογισμός αυτός περιμένουμε ότι δεν μπορεί να γίνει «ακριβώς» δεδομένου ότι το $\pi$ είναι άρρητος αριθμός. Αυτό όμως που μπορεί να γίνει είναι να προσεγγίσουμε τον λόγο $A_c/A_s$, και μέσω αυτού τον αριθμό $\pi$, με μια συγκεκριμένη ακρίβεια. Ο υπολογισμός κάθε εμβαδού απαιτεί τον υπολογισμό του αντίστοιχου ολοκληρώματος. Μια επιλογή για να επιτευχθεί αυτό θα ήταν η αριθμητική ολοκλήρωση. Αυτό θα μπορούσε να γίνει με διάφορες αριθμητικές μεθόδους, όπως ο κανόνας του τραπεζίου και οι εξισώσεις τύπου Newton – Cotes (π.χ.. Simpson’s rule). Μια εναλλακτική επιλογή αριθμητικής ολοκλήρωσης για τον υπολογισμό θα ήταν η ακόλουθη διαδικασία (ολοκλήρωση Monte Carlo):

• •

  Δημιουργία $N$ τυχαίων σημείων μέσα στο τετράγωνο.

• •

  Εύρεση του αριθμού των σημείων, εκ των $N$ τυχαίων σημείων που βρίσκονται στο τετράγωνο, τα οποία βρίσκονται επίσης μέσα στον κύκλο. Έστω Μ αυτά τα σημεία.

• •

  Συνεπώς ο αριθμός $\pi$ προσεγγίζεται ως

  $$\pi (N)=4\frac{M}{N}.$$

Η παραπάνω διαδικασία προσέγγισης ενός ολοκληρώματος (εδώ εμβαδού ενός γεωμετρικού σχήματος) με τη χρήση τυχαίων αριθμών, είναι ένας πολύ απλός αλγόριθμος Monte Carlo, ο οποίος μπορεί εύκολα να υλοποιηθεί μέσα σε λίγες γραμμές κώδικα από κάθε φοιτητή (ή μαθητή) ο οποίος γνωρίζει μια οποιοδήποτε γλώσσα προγραμματισμού. Η υλοποίηση του παραπάνω αλγορίθμου προτείνεται ως άσκηση για τον αναγνώστη.

Η γραφική αναπαράσταση του παραπάνω αλγορίθμου φαίνεται στο παρακάτω διάγραμμα (Σχήμα 7.1), για ένα συγκεκριμένο υπολογιστικό «πείραμα».

Προσέξτε ότι ο λόγος $M/N$ προσεγγίζει τον λόγο των δύο εμβαδών για μεγάλα $N$, δηλαδή

$$\frac{A_c}{A_s}=\underset{N\to \mathrm{\infty }}{lim}\mathrm{}\frac{M}{N}.$$

Συνεπώς η προσέγγιση του λόγου των δύο εμβαδών και κατ’ επέκταση του αριθμού $\pi$ βελτιώνεται όσο μεγαλύτερος είναι ο αριθμός των «τυχαίων σημείων» $N$.

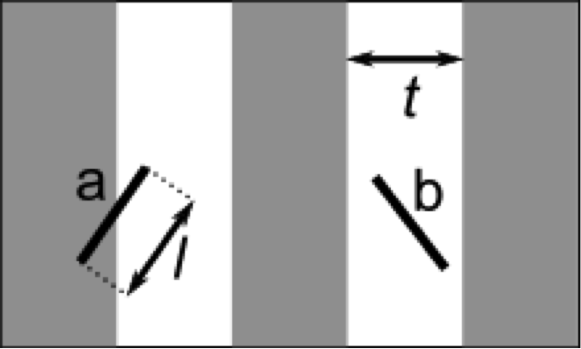
Ο πρώτος (;) αλγόριθμος τύπου Monte Carlo αναπτύχθηκε από τον Buffon το 1777. Στην πραγματικότητα είναι ένας ακόμη αλγόριθμος υπολογισμού του αριθμού π, λίγο πιο περίπλοκος από τον αλγόριθμο που είδαμε παραπάνω. Έστω το παρακάτω πρόβλημα. Υποθέστε ότι έχουμε ένα χώρο με παράλληλες ξύλινες πλάκες, με ακριβώς το ίδιο πάχος, και πετάμε σε αυτόν μια βελόνα. Το πάχος κάθε πλάκας είναι t και το μήκος κάθε βελόνας l.

Ερώτηση: Ποια είναι η πιθανότητα, P, η βελόνα να διασταυρώνει μια γραμμή (την ένωση) μεταξύ δύο πλακών; (Δες Σχήμα 7.2)

Απάντηση: Θεωρούμε ότι ρίχνουμε τυχαία βελόνες μέσα στο χώρο. Αν υποθέσουμε ότι το μήκος κάθε βελόνας είναι μικρότερο του πάχους των πλακών, δηλαδή l ¡ t , τότε η ζητούμενη πιθανότητα είναι:

$$P=\frac{2l}{\pi t}.$$

(7.4)

Η απόδειξη της παραπάνω σχέσης αφήνεται ως άσκηση στον αναγνώστη.

Όπως βλέπουμε η παραπάνω σχέση μπορεί να χρησιμοποιηθεί για τον υπολογισμό του αριθμού $\pi$. Πιο συγκεκριμένα, ο αλγόριθμος υπολογισμού του $\pi$ με βάση το παραπάνω πείραμα θα ήταν ο εξής:

• •

  Πρώτα δημιουργούμε «τυχαία» $N$ βελόνες μέσα στο χωρίο μας. Αυτό επιτυγχάνεται με τη χρήση τυχαίων μεταβλητών μέσα σε ένα συγκεκριμένο χωρίο. Κάθε βελόνα περιγράφεται από 2 τ.μ., τη θέση του κέντρου της και τη γωνία ως προς τη κάθετη γραμμή (ένωση) μεταξύ δύο πλακών.

• •

  Κατόπιν μετράμε πόσες από αυτές διασταυρώνονται με τις γραμμές (ενώσεις) μεταξύ των πλακών. Έστω ότι αυτές είναι $M$.

• •

  Η πιθανότητα διασταύρωσης είναι $P=M/N$. Άρα τελικά: $\pi \simeq \frac{2l}{Pt}=\frac{N}{M}\frac{2l}{t}$.