7 Στοχαστικά Συστήματα – Μέθοδοι Monte Carlo 7.2 Αλγόριθμοι Monte Carlo 7.4 Αλγόριθμοι Monte Carlo Μαρκοβιανών Αλυσίδων

7.3 Γεννήτριες Τυχαίων Αριθμών

Από τα παραπάνω απλά παραδείγματα ολοκλήρωσης Monte Carlo παρατηρούμε ότι το κοινό στοιχείο των μεθόδων επίλυσής τους είναι η δημιουργία «τυχαίων αριθμών» από μια κατανομή, ή αλλιώς η δειγματοληψία της συγκεκριμένης κατανομής. Η σωστή δειγματοληψία, την οποία συχνά περιγράφουμε και ως προσομοίωση, είναι το πρώτο και σημαντικότερο βήμα σε κάθε αλγόριθμο Monte Carlo, καθώς το στοχαστικό μοντέλο θα επιλυθεί χρησιμοποιώντας τους τυχαίους αριθμούς, οι οποίοι έχουν προκύψει από την συγκεκριμένη δειγματοληψία. Οι τυχαίοι αριθμοί είναι μια πολύ σημαντική έννοια στη θεωρία πιθανοτήτων και γενικότερα στην στατιστική ανάλυση. Τι είναι όμως οι «τυχαίοι αριθμοί» και πως δημιουργούνται; Όπως είδαμε και στην εισαγωγή τυχαίοι αριθμοί είναι μια ακολουθία αριθμών, η οποία έχει τις παρακάτω ιδιότητες:

(α)

Οι τιμές των αριθμών κατανέμονται μέσα σε ένα διάστημα, ακολουθώντας κάποια συγκεκριμένη κατανομή (συνήθως την ομοιόμορφη), και
(β)

Δεν υπάρχει καμία συσχέτιση μεταξύ των αριθμών. Δηλαδή δεν μπορούμε να προβλέψουμε τις επόμενες (μελλοντικές) τιμές των αριθμών δεδομένων των προηγούμενων τιμών τους.

Οι τυχαίοι αριθμοί είναι μια πρωταρχική έννοια σε κάθε αλγόριθμο Monte Carlo και γενικότερα στοχαστικής μοντελοποίησης – προσομοίωσης. Συνδέονται δε άμεσα με την έννοια των τυχαίων μεταβλητών, που είδαμε παραπάνω.

Ορισμός.

Γεννήτρια Τυχαίων Αριθμών: Γεννήτρια τυχαίων αριθμών ονομάζουμε τον αλγόριθμο δημιουργίας τυχαίων αριθμών σε κάποιο διάστημα, ακολουθώντας κάποια συγκεκριμένη κατανομή. Συνήθως το διάστημα είναι το $[0,1]$ και οι αριθμοί δημιουργούνται έτσι ώστε να υπακούουν την Ομοιόμορφη Κατανομή (uniform distribution). Πιο συγκεκριμένα αν $u=\{u_{1},u_{2},\ldots,u_{n}\}$ είναι μια σειρά $n$ τυχαίων αριθμών, η γεννήτρια:

•

Ξεκινώντας από μια αρχική τιμή u0 δημιουργεί, μέσω μιας σχέσης Di(u0), την σειρά (ui) στο διάστημα [0, 1].
•

Οι τιμές $\{u_{1},u_{2},\ldots,u_{n}\}$ πρέπει να αναπαράγουν τη συμπεριφορά ομοιόμορφων τυχαίων μεταβλητών, δηλαδή να υπακούουν την κατανομή $U[0,1]$ .

Παρατήρηση 7.2.

«Φιλοσοφικό Παράδοξο»: Προσέξτε ότι οι «τυχαίοι αριθμοί» δημιουργούνται από ένα ντετερμινιστικό αλγόριθμο. Για το λόγο αυτό ονομάζονται και ψεύδο-τυχαίοι. Λόγω ακριβώς της ντετερμινιστικής τους φύσης οι παραπάνω αλγόριθμοι επαναλαμβάνουν περιοδικά την ίδια ακολουθία τυχαίων αριθμώ, αν ξεκινήσουν από ακριβώς τις ίδιες αρχικές συνθήκες.

Ορισμός.

Περίοδος Γεννήτριας Τυχαίων Αριθμών: Περίοδος ενός αλγορίθμου δημιουργίας τυχαίων αριθμών είναι ο ακέραιος αριθμός $m$ για τον οποίο ισχύει:

u_{i+m}=u_{i}.

Η επαναλαμβανόμενη σειρά τυχαίων αριθμών δεν είναι σημαντικό πρόβλημα όσο το μέγεθός της δεν ξεπερνά την περίοδο του αλγορίθμου. Αν όμως την ξεπεράσει μπορεί να δημιουργήσει πρόβλημα λόγω της ισχυρής συσχέτισης μεταξύ των δημιουργούμενων αριθμών. Παρακάτω θα δούμε αναλυτικά τρόπους – αλγορίθμους δημιουργίας «τυχαίων», ή καλύτερα ψευδό-τυχαίων αριθμών.

7.3.1 Ομοιόμορφη Κατανομή

Όπως είδαμε και παραπάνω, η πιο συνηθισμένη σειρά τυχαίων αριθμών αφορά μια ακολουθία αριθμών στο διάστημα $[0,1]$ , η οποία ακολουθεί την ομοιόμορφη κατανομή, δηλαδή την $U[0,1]$ . Στο κεφάλαιο αυτό θα εξετάσουμε δύο διαφορετικούς αλγόριθμους δημιουργίας τυχαίων αριθμών από την ομοιόμορφη κατανομή.

Αλγόριθμος «Συμβατική Γεννήτρια»

Ο πρώτος αλγόριθμος που θα δούμε είναι η συμβατική γεννήτρια (congruential generator) τυχαίων αριθμών. Έστω $X=[X_{i}]\;(i=1,2,\ldots,n)$ μία σειρά n τυχαίων αριθμών. Η σειρά αναπαράγεται μέσω της σχέσης:

Y_{i}=D(x)=(aY_{i-1}+b)\mod(M),\qquad X_{i}=\frac{Y_{i}}{M}

(7.5)

όπου $a, b, M$ είναι σταθερές (ακέραιοι φυσικοί αριθμοί). Το δεξί μέλος της παραπάνω σχέσης υποδηλώνει το υπόλοιπο της διαίρεσης των ακεραίων αριθμών $M$ και $(aY_{i}-1+b)$ .

Πιο συγκεκριμένα, ο αλγόριθμος αποτελείται από τα παρακάτω βήματα:

(α)

Αρχικά επιλέγουμε τις τιμές των ακεραίων $a, b, M$ καθώς και μία αρχική τιμή (“seed”) $Y_{0}\in\{1,2,\ldots,M-1\}$ .
(β)

Για $i=1,2,\ldots$ υπολογίζουμε μέσω των παραπάνω σχέσεων την ακέραια μεταβλητή $Y_{i}$ και την πραγματική $X_{i}$ .

Ο αλγόριθμος αυτός είναι αρκετά απλός και μια υλοποίηση του παρουσιάζεται στο Παράρτημα του κεφαλαίου σε γλώσσα MATLAB. Πώς ξέρουμε όμως ότι ο παραπάνω αλγόριθμος είναι μια «καλή» γεννήτρια τυχαίων αριθμών; Όπως αναφέραμε θα πρέπει να ελέγξουμε:

(α)

Αν αναπαράγει την ομοιόμορφη κατανομή στο διάστημα $[0,1]$ , και
(β)

Αν υπάρχει συσχέτιση μεταξύ των τυχαίων αριθμών που δημιουργεί.

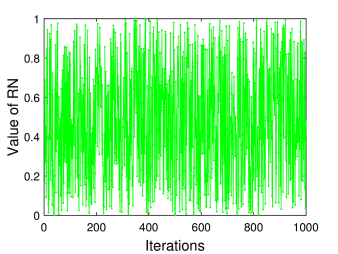
Κατόπιν υλοποιούμε τον παραπάνω αλγόριθμο για συγκεκριμένες τιμές των σταθερών. Αποτελέσματα φαίνονται στο παρακάτω διάγραμμα (Σχήμα 7.3). Πρώτα, στο Σχήμα 7.3α βλέπουμε ενδεικτικά μια σειρά $n_{1}(=1000)$ τυχαίων αριθμών. Όπως παρατηρούμε όλοι οι αριθμοί βρίσκονται, όπως θα περιμέναμε, μέσα στο επιθυμητό διάστημα $[0,1]$ ενώ ακολουθούν μια αρκετά «ακανόνιστη» τροχιά.

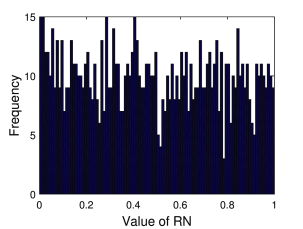
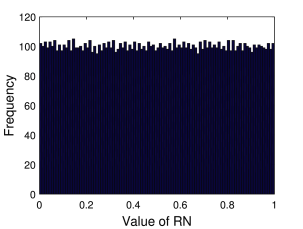
Στο Σχήμα 7.3β βλέπουμε την κατανομή αυτών, η οποία όπως βλέπουμε προσεγγίζει την ομοιόμορφη κατανομή. Ο συγκεκριμένος αριθμός όμως δεν είναι ακόμη αρκετά μεγάλος για να αναπαράγει με ακρίβεια την ομοιόμορφη κατανομή. Στο Σχήμα 7.3γ βλέπουμε την κατανομή ενός μεγαλύτερου αριθμού τυχαίων αριθμών $n_{2}(=10000)$ . Όπως βλέπουμε η κατανομή αυτών είναι πολύ πιο «κοντά» στην ομοιόμορφη. Αυτό είναι κάτι που περιμένουμε καθώς όσο αυξάνει η δειγματοληψία από μια συγκεκριμένη κατανομή, τόσο περισσότερο θα πρέπει η κατανομή των δειγματοληπτούμενων Τ.Μ. θα πρέπει να προσεγγίζει τη κατανομή αυτή. Στο όριο που ο αριθμός αυτός φτάνει στο άπειρο θα πρέπει να αναπαράγεται ακριβώς η συγκεκριμένη κατανομή.

Σχήμα 7.3: Τυχαίοι αριθμοί που ακολουθούν την ομοιόμορφη κατανομή από τον αλγόριθμο «συμβατική γεννήτρια»: (α) Μια «Χρονό-σειρά» $n=1000$ τυχαίων αριθμών. (β) Κατανομή συχνοτήτων $n=1000$ τυχαίων αριθμών. (γ) Κατανομή συχνοτήτων $n=10000$ τυχαίων αριθμών.

Ερώτηση κατανόησης 7.3.

Για ποιο λόγο η κατανομή συχνοτήτων στο Σχήμα 7.3γ για $n=10000$ έχει τιμές περίπου ίσες με 100; Θα άλλαζε αυτός ο αριθμός αν άλλαζε ο αριθμός των τυχαίων αριθμών $n$ ;

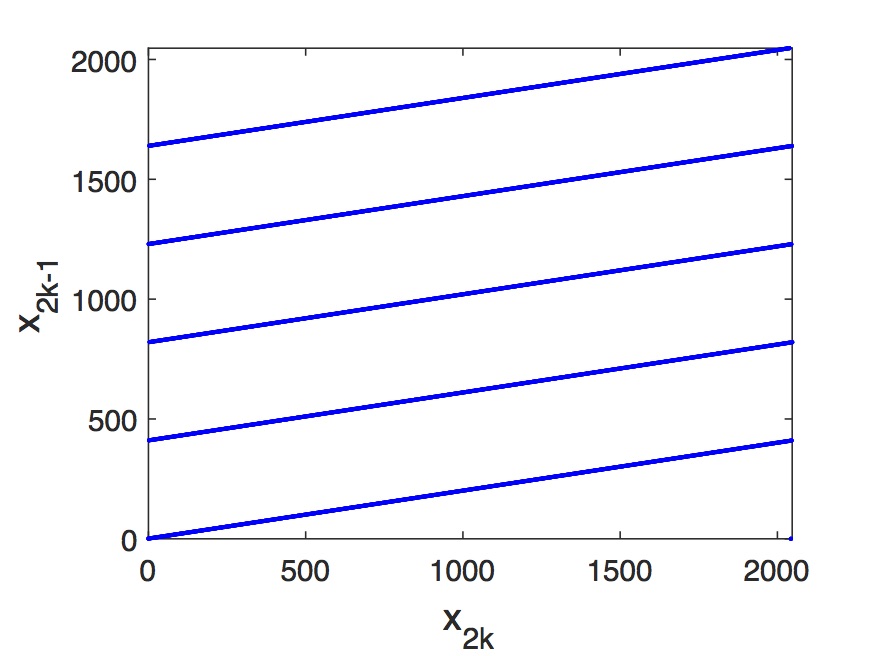
Σε δεύτερο στάδιο ελέγχουμε το αν υπάρχει συσχέτιση μεταξύ των διαφορετικών τυχαίων αριθμών. Αν υπάρχει θα περιμέναμε να είναι πιο ισχυρή μεταξύ διαδοχικών τυχαίων αριθμών. Για το λόγο αυτό ελέγχουμε τη συσχέτιση με διαγράμματα διαδοχικών αριθμών τύπου $X_{2k}$ vs. $X_{2k+1}$ όπου $k=1,2,\ldots$ , δηλαδή άρτιων-περιττών. Αν δεν υπάρχει συσχέτιση τα ζευγάρια $(X_{2k},X_{2k+1})$ μπορούν να πάρουν κάθε τιμή στο [0-1, 0-1], ενώ αν υπάρχει συσχέτιση δεν είναι όλα τα ζευγάρια δυνατά και δημιουργούνται συγκεκριμένα «μοτίβα». Στο Σχήμα 7.4 παρουσιάζουμε τα ζευγάρια $(X_{2k},X_{2k+1})$ από την παραπάνω υλοποίηση. Βλέπουμε ότι, τουλάχιστον για τις συγκεκριμένες τιμές των σταθερών του αλγορίθμου, υπάρχει ισχυρή συσχέτιση μεταξύ διαδοχικών τυχαίων αριθμών. Συνεπώς ο συγκεκριμένος αλγόριθμος δεν είναι η καλύτερη δυνατή λύση.

Σχήμα 7.4: Συσχέτιση μεταξύ διαδοχικών τυχαίων αριθμών που ακολουθούν την ομοιόμορφη κατανομή από τον αλγόριθμο συμβατική γεννήτρια.

Αλγόριθμος «Mersenne Twister»

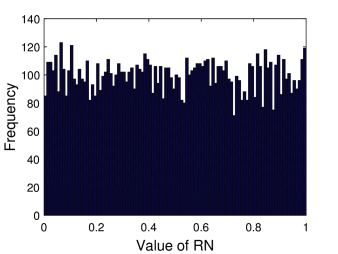
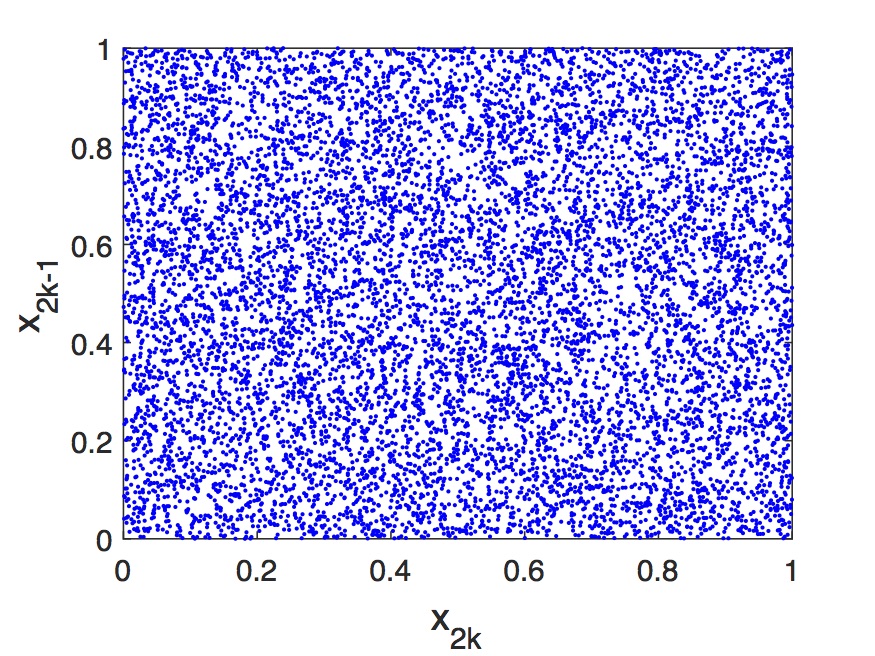
Ο δεύτερος αλγόριθμος που θα δούμε είναι ο αλγόριθμος Mersenne Twister. Αυτός είναι ένας ιδιαίτερα πολύπλοκος αλγόριθμος που χρησιμοποιείται σε πολλά πακέτα μοντελοποίησης για την ακριβή δημιουργία τυχαίων αριθμών. Επίσης είναι ενσωματωμένη συνάρτηση και προεπιλεγμένη γεννήτρια τυχαίων αριθμών σε διάφορες γλώσσες προγραμματισμού, όπως η γλώσσα MATLAB (συνάρτηση rand). Τα αποτελέσματα από την εφαρμογή του αλγορίθμου Mersenne Twister φαίνονται παρακάτω στο Σχήμα 7.5. Αρχικά στο Σχήμα 7.5α βλέπουμε την κατανομή $n(n=1000)$ τυχαίων αριθμών η οποία όπως θα περιμέναμε προσεγγίζει πολύ καλά την ομοιόμορφη κατανομή. Κατόπιν στο Σχήμα 7.5β εξετάζουμε συσχέτιση μεταξύ διαδοχικών αριθμών μέσω γραφημάτων $X_{2k}$ vs. $X_{2k+1}$ όπως και παραπάνω. Είναι ξεκάθαρο ότι δεν υπάρχει καμία συσχέτιση μεταξύ διαδοχικών τυχαίων αριθμών.

Σχήμα 7.5: Δημιουργία $n$ τυχαίων αριθμών που ακολουθούν την ομοιόμορφη κατανομή από τον αλγόριθμο Mersenne Twister $(n=10000)$ . (α) Κατανομή συχνοτήτων (β) Συσχέτιση μεταξύ διαδοχικών τυχαίων αριθμών.

Ερώτηση κατανόησης 7.4.

Πώς μπορούν οι κατανομές συχνοτήτων (Σχήματα 7.3β, 7.3γ και 7.5α) να γίνουν κατανομές πιθανοτήτων;

Συμπερασματικά μια καλή γεννήτρια τυχαίων αριθμών είναι ένας ντετερμινιστικός αλγόριθμος ο οποίος θα πρέπει:

(α)

να αναπαράγει την συγκεκριμένη κατανομή,
(β)

να μην υπάρχει συσχέτιση μεταξύ των τ.μ., και
(γ)

να έχει αρκετά μεγάλη περίοδο.

Σήμερα υπάρχουν πλέον αρκετά καλοί τέτοιοι αλγόριθμοι, οι οποίοι είναι ενσωματωμένοι ως εσωτερικές συναρτήσεις σε κάθε γλώσσα προγραμματισμού.

7.3.2 Αντίστροφη Μέθοδος

Όπως είδαμε παραπάνω η δειγματοληψία τυχαίων μεταβλητών από την ομοιόμορφη κατανομή μπορεί να γίνει με μεγάλη επιτυχία. Τι γίνεται όμως αν επιθυμούμε δειγματοληψία από μια διαφορετική κατανομή; Αυτό είναι ένα αρκετά δύσκολο πρόβλημα το οποίο δεν έχει λύση για οποιαδήποτε κατανομή.

Στην πραγματικότητα μπορούμε να πάρουμε απ’ευθειας δειγματοληψία, μόνο από ένα μικρό αριθμό κατανομών. Υπάρχει όμως ένα θεώρημα που μας επιτρέπει να πάρουμε από μία κατανομή αν ξέρουμε την αντίστροφη συνάρτηση κατανομής. Παρακάτω, πρώτα ορίζουμε την αντίστροφη συνάρτηση και μετά δίνουμε ένα παράδειγμα δειγματοληψίας από μια κατανομή, χρησιμοποιώντας την αντίστροφή της.

Ορισμός.

Αντίστροφη Συνάρτηση (Inverse Function): Για μια συνάρτηση $F\to R$ η αντίστροφή της $F^{-}$ είναι η:

F^{-}(u)=\inf\{x:\;F(x)\geq u\}.

(7.6)

Λήμμα.

Έστω $U$ μια τυχαία μεταβλητή με $u\sim{\rm Uniform}(0,1)$ και $F$ η προσθετική συνάρτηση κατανομής. Τότε η τ.μ. $X=F^{-}(u)$ έχει κατανομή $f(.)$ όπου $F^{-}(u)=\inf\{x:\,F(x)\geq u\}$ .

Σύντομο πρόβλημα 7.1.

Αποδείξτε το παραπάνω Λήμμα.

Υπενθυμίζουμε εδώ τον ορισμό της προσθετικής συνάρτησης κατανομής.

Ορισμός.

Προσθετική Συνάρτηση Κατανομής (Cumulative Distribution Function) Έστω μια τυχαία μεταβλητή $X$ . Η συνάρτηση:

F(x)=P(X\leq x)

(7.7)

ονομάζεται προσθετική συνάρτηση κατανομής.

Παράδειγμα 7.1.

Εκθετική κατανομή. Η εκθετική κατανομή είναι μια οικογένεια κατανομών η οποία ορίζεται, για ένα δεδομένο φυσικό αριθμό $\lambda$ , ως:

{\rm Exp}(\lambda)=\begin{cases}\lambda\exp⁡(-\lambda x),\qquad x\geq 0\\ 0,\qquad\qquad\qquad x<0\end{cases}.

(7.8)

Έστω μια τυχαία μεταβλητή, $X$ , η οποία υπακούει την εκθετική κατανομή με $\lambda=1$ , δηλαδή: $X\sim{\rm Exp}(1)$ . Η προσθετική συνάρτηση κατανομής είναι: $F(x)=1-\exp⁡(-x)$ . Υπολογίζοντας την αντίστροφη συνάρτηση, δηλαδή λύνοντας ως προς $x$ , έχουμε την: $u=1-\exp⁡(-x)\Rightarrow x=-\log⁡(1-u)$ . Άρα, για $u\sim U(0,1)$ η $x=-\log⁡(u)$ ακολουθεί την εκθετική κατανομή.

Παρατήρηση 7.3.

Προσέξτε ότι σε αυτό το παράδειγμα χρησιμοποιήσαμε την ιδιότητα ότι αν η $u$ είναι τ.μ. που ακολουθεί την ομοιόμορφη κατανομή στο $(0,1)$ τότε το ίδιο ισχύει και για την $(1-u)$ , δηλαδή αν $u\sim U(0,1)$ και η $(1-u)\sim U(0,1)$ .

Παρατήρηση 7.4.

Η εφαρμογή της παραπάνω μεθόδου απαιτεί ακριβής γνώση (υπολογισμό) της προσθετικής συνάρτησης κατανομής. Σε πολλές περιπτώσεις (κατανομές) αυτό δεν είναι εφικτό.

Ερώτηση κατανόησης 7.5.

Ποια είναι η προσθετική συνάρτησης κατανομής της κανονικής κατανομής;

7.3.3 Κανονική Κατανομή

Στην πραγματικότητα μπορούμε να πάρουμε απευθείας δειγματοληψία, μόνο από ένα μικρό αριθμό κατανομών. Από τις κατανομές αυτές πιο σημαντική είναι η κανονική κατανομή καθώς σε πολλά προβλήματα εμφανίζονται τυχαίες μεταβλητές οι οποίες υπακούουν την κανονική κατανομή. Παρακάτω περιγράφουμε ένα αλγόριθμο δημιουργίας τ.μ. από την κανονική κατανομή.

Αλγόριθμος Box – Muller

Θεωρήστε ζευγάρι τ.μ. $(X_{1},X_{2})$ και τις αντίστοιχες πολικές συντεταγμένες $(R,\theta)$ , όπου:

X_{1}=R\cos\theta,\quad X_{2}=R\sin\theta.

(7.9)

Αν οι $X_{1},X_{2}$ έρχονται από την κανονική κατανομή με μέση τιμή 0 και διασπορά 1, $N(0,1)$ τότε , η τ.μ. $\theta$ έρχεται από την ομοιόμορφη κατανομή στο $0-2\pi$ , $U(0,2\pi)$ και η $R_{2}$ από την εκθετική κατανομή με $\lambda=1/2,{\rm Exp}(1/2)$ .

Σύντομο πρόβλημα 7.2.

Αποδείξτε την παραπάνω ιδιότητα.

Συνεπώς ένας αλγόριθμος δημιουργίας τ.α. από την κανονική κατανομή είναι ο ακόλουθος:

(α)

Δημιουργία μιας τ.μ. («γωνίας») $\theta\sim U(0,2\pi)$ και μιας δεύτερης τ.μ. («ακτίνας») $R_{2}\sim{\rm Exp}(1/2)$ . Υπενθυμίζουμε ότι στα προηγούμενα υπο-κεφάλαια είδαμε τρόπους δημιουργίας τ.μ. τόσο από την ομοιόμορφη όσο και από την εκθετική κατανομή.
(β)

Μετατροπή των τ.μ. $\theta$ και $R$ στις καρτεσιανές συντεταγμένες από τις παραπάνω σχέσεις (7.9).
(γ)

Επιστροφή στο βήμα (α).

Στο Σχήμα 7.6 παρουσιάζεται η κατανομή που ακολουθούν $n(n=10000)$ τυχαίοι αριθμού που έχουν δημιουργηθεί από τον παραπάνω αλγόριθμο. Όπως βλέπουμε ότι προσεγγίζουν με μεγάλη ακρίβεια την κανονικά κατανομή.

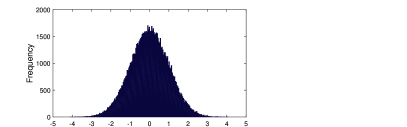
Σχήμα 7.6: Κατανομή $n\,(n=100000)$ τυχαίων αριθμών που ακολουθούν την κανονική κατανομή από τον αλγόριθμο Box-Muller.

7.3.4 Μέθοδοι Αποδοχής – Απόρριψης

Όπως αναφέραμε και παραπάνω στη γενική περίπτωση δεν μπορούμε να πάρουμε δειγματοληψία, για μια τ.μ. $X$ , από οποιαδήποτε πυκνότητα πιθανότητας $f(.)$ . Μια εναλλακτική μέθοδο σε αυτή την περίπτωση είναι οι εφαρμογή μεθόδων αποδοχής-απόρριψης (accept-reject).

Βασική ιδέα των μεθόδων αποδοχής – απόρριψης: Δειγματοληπτούμε την τ.μ. $X$ από μια άλλη πυκνότητα $g(.)$ η οποία είναι σχετικά παρόμοια της $f(.)$ , και από την οποία μπορούμε να πάρουμε δειγματοληψία.

Η παραπάνω ιδέα βασίζεται στο παρακάτω θεώρημα:

Θεώρημα.

Πρωταρχικό Θεώρημα προσομοίωσης (Fundamental Theorem of Simulation). Η προσομοίωση της τ.μ. $X\sim F(x)$ είναι ισοδύναμη με την προσομοίωση του ζευγαριού τ.μ. $(X,U)\sim U\{(x,u):\;0<u<F(x)\}$ .

Το παραπάνω θεώρημα δεν μας βοηθά άμεσα καθώς η προσομοίωση του ζευγαριού $(X,U)$ είναι εξίσου δύσκολη με αυτή της αρχικής μεταβλητής. Αυτό όμως που μπορεί να γίνει είναι η προσομοίωση του ζευγαριού $(X,U)$ σε ένα μεγαλύτερο σύνολο και κατόπιν η τελική επιλογή του ζευγαριού που ικανοποιεί τον παραπάνω περιορισμό.

Αλγόριθμος Αποδοχής – Απόρριψης (Accept – Reject or Rejection Sampling Algorithm)

Έστω δύο πυκνότητες $f(.),g(.)$ με $f(x)<Mg(x)$ για κάθε $x$ . Μπορούμε να δημιουργήσουμε δείγμα από την $f(.)$ μέσω του παρακάτω αλγορίθμου:

(α)

Δημιουργία $X\sim g,\,U\sim U[0,1]$
(β)

Αποδοχή $Y=X$ με πιθανότητα $f(x)/Mg(x)$
(γ)

Επιστροφή στο βήμα (α).

Τελικά εύκολα δείχνουμε ότι για κάθε μετρήσιμο σύνολο $Α$ οι τιμές της $X$ είναι από την κατανομή $f(.)$ :

P(X\leq x)=P(Y\leq x\,|\,U<F(y))=\frac{\int_{a}^{x}\int_{0}^{F(y)}dudy}{\int_{% a}^{b}\int_{0}^{F(y)}dudy}=\int_{a}^{x}F(y)dy.

(7.10)

Με άλλα λόγια αν θεωρήσουμε ότι οι τ.μ. που θέλουμε να δημιουργήσουμε βρίσκονται μέσα σε ένα σύνολο τιμών $Α$ και δημιουργήσουμε ομοιόμορφο δείγμα τ.μ. από ένα υπερσύνολό του $Β$ , τότε κρατώντας μόνο τους όρους που είναι και μέσα στο $Α$ μπορούμε τελικά να έχουμε ένα ομοιόμορφο δείγμα στο $Α$ .