5 Μαθηματική Βιολογία – Πληθυσμιακά Μοντέλα Ενός Είδους 5.2 Συνεχή Πληθυσμιακά Μοντέλα Ενός Είδους 5.4 Μελέτη

5.3 Διακριτά Πληθυσμιακά Μοντέλα Ενός Είδους

Όπως αναφέραμε στην αρχή του κεφαλαίου η θεώρηση του πληθυσμού ως συνεχή μεταβλητή ως προς το χρόνο (συνεχή μοντέλα) είναι καλή προσέγγιση για:

(α)

περιπτώσεις που οι χρονικές περίοδοι που μελετάμε είναι μεγάλες σε σχέση με την περίοδο αναπαραγωγής του είδους, ή/και
(β)

οι διαφορετικές γενεές αλληλεπικαλύπτονται (π.χ. άνθρωποι).

Όπως όμως είδαμε στην αρχή του κεφαλαίου για πολλά βιολογικά είδη οι παραπάνω υποθέσεις δεν είναι καλές (π.χ. έντομα, βακτήρια, ιοί, κλπ.). Επιπλέον, περιμένουμε η περιγραφή του πληθυσμού ως διακριτή μεταβλητή ως προς το χρόνο, να είναι καλύτερη προσέγγιση, εφόσον και στην πραγματικότητα η αναπαραγωγή γίνεται σε διακριτά διαστήματα. Στις περιπτώσεις αυτές οι πληθυσμοί μεταβάλλονται σε διακριτά βήματα και αντίστοιχα πρέπει η μελέτη τους να γίνει χρησιμοποιώντας εξισώσεις διαφορών (difference equations).

Στα διακριτά μοντέλα η τιμή μιας ποσότητας $P$ εκφράζεται ως συνάρτηση της προηγούμενης τιμής της. Για μια χρονική μεταβλητή αυτό εκφράζεται ως: $P_{t+1}=F(P_{t})$ .

Ακολουθούν χαρακτηριστικά παραδείγματα διακριτών μοντέλων, ξεκινώντας από υποθέσεις παρόμοιες με αυτές των συνεχών μοντέλων που είδαμε παραπάνω. Γιατί όμως να μελετήσουμε «παρόμοια» μοντέλα; Όπως θα δούμε τα διακριτά μοντέλα μπορεί να έχουν σημαντικές ποιοτικές διαφορές σε σχέση με τα συνεχή, ακόμη και αν έχουν προκύψει από τις ίδιες αρχικές υποθέσεις!

5.3.1 Διακριτό Μαλθουσιανό Μοντέλο

Πρώτα θα εξετάσουμε το Μαλθουσιανό μοντέλο σε διακριτή μορφή.

Ερώτηση κατανόησης 5.5.

Περιμένουμε διαφορετική συμπεριφορά από την εκθετική που είδαμε στη συνεχή του μορφή;

Έστω ένα είδος σε ελεγχόμενες συνθήκες εργαστηρίου, το οποίο μελετάται σε διαδοχικές διακριτές χρονικές περιόδους. Ο πληθυσμός του είδους σε χρόνο t συμβολίζεται ως $P_{t}$ . Αν αντίστοιχα με το συνεχές μοντέλο περιγράφουμε τις:

•

Γεννήσεις (birth) ως $(bP)$ , όπου b είναι το ποσοστό γεννήσεων
•

Θάνατοι (death) ως $(dP)$ , όπου d είναι το ποσοστό θανάτων
•

Υποθέτουμε ότι η μετανάστευση δεν συνεισφέρει στη μεταβολή του πληθυσμού.

Ερώτηση κατανόησης 5.6.

Γενικά πρέπει να ισχύει $b>0$ και $0<d<1$ . Γιατί;

Η αλλαγή του πληθυσμού σε μία χρονική περίοδο, ή μονάδα χρόνου, είναι:

\Delta P=bP-dP=(b-d)P

και το μοντέλο γίνεται:

P_{t+1}=P_{t+1}+(b-d)P_{t}=(1+b-d)P_{t}=rP_{t}(5.13)

(5.15)

όπου $r$ είναι ο (διακριτός) ρυθμός μεταβολής του πληθυσμού. Προσέξτε ότι για να μην υπάρχει μείωση του πληθυσμού πρέπει $r>1$ .

Έστω επίσης ότι η αρχική κατάσταση του πληθυσμού είναι $P(t=0)=P_{0}$ .

Ερώτηση κατανόησης 5.7.

Πως συγκρίνεται αυτή η συνθήκη με την αντίστοιχη για το συνεχές εκθετικό μοντέλο; Είναι κάτι που το περιμένετε;

Προσέξτε επίσης ότι το χρονικό διάστημα (μονάδα χρόνου) μεταξύ των διαφορετικών τιμών, εξαρτάται από το είδος το οποίο μελετάμε.

Ερώτηση κατανόησης 5.8.

Ποια είναι η κατάλληλη μονάδα χρόνου για τα παρακάτω συστήματα: άνθρωποι, ελέφαντες, ψάρια, βακτήρια;

Από μαθηματικής πλευράς εύκολα βλέπουμε ότι το παραπάνω πρόβλημα έχει «ακριβής» λύση: Έστω ότι η αρχική τιμή $(t=0)$ του πληθυσμού είναι $P_{0}$ . Τότε, η μεταβολή του πληθυσμού είναι:

1η χρονική περίοδος: $P_{1}=rP_{0}$
2η χρονική περίοδος: $P_{2}=rP_{1}=r^{2}P_{0}$
…
$n$ -οστη χρονική περίοδος: $P_{n}=r^{n}P_{0}$

δηλαδή ο πληθυσμός μπορεί να προβλεφθεί σε κάθε χρονική στιγμή, μόνο από τις σταθερές $\lambda$ και $P_{0}$ .

Παράδειγμα 5.1.

Έστω οργανισμός με πολύ συγκεκριμένο κύκλο ζωής (π.χ. έντομα) στον οποίο κάθε θηλυκό γεννάει 100 αυγά. Κατόπιν όλοι οι ενήλικες πεθαίνουν. Μετά από τα αυγά ένα ποσοστό (π.χ. το 10%) γίνεται ενήλικα θηλυκά, τα υπόλοιπα δεν προλαβαίνουν να ενηλικιωθούν (πεθαίνουν) ή γίνονται αρσενικά. Βρείτε τη μεταβολή του πληθυσμού.

Επίλυση.

Θεωρούμε το διακριτό μοντέλο που περιγράψαμε παραπάνω. Οι παράμετροι του μοντέλου είναι:

•

$d=1$ , καθώς σε μια χρονική περίοδο πεθαίνουν όλοι οι ενήλικες, και
•

$b=0.10\times 100=10$ , καθώς σε μια χρονική περίοδο γεννάει 100 αυγά κάθε θηλυκό, και τα θηλυκά είναι το 10% των αυγών.
•

Περιγράφουμε μόνο το θηλυκό πληθυσμό.

Τελικά το μοντέλο για το συγκεκριμένο παράδειγμα είναι:

P_{t+1}=(1+10-1)P_{t}=10P_{t}.

Σύντομο πρόβλημα 5.4.

Ποιά πρέπει να είναι η σταθερά $b$ ώστε ο πληθυσμός $P_{t}$ να είναι σταθερός;

Ερώτηση κατανόησης 5.9.

Στην ανάπτυξη του παραπάνω μοντέλου αμελήσαμε τον αρσενικό πληθυσμό. Γιατί; Μπορείτε να σκεφτείτε περιπτώσεις όπου το να αμελούμε τον αρσενικό πληθυσμό δεν είναι καλή υπόθεση;

Προσέξτε ότι το παραπάνω μοντέλο είναι γραμμικό και προβλέπει συνεχή αύξηση του πληθυσμού. Μας «θυμίζει» συνεπώς το συνεχές Μαλθουσιανό μοντέλο, καθώς παρουσιάζει παρόμοια με την εκθετική μεταβολή. Επίσης βασική υπόθεση στο μοντέλο είναι ότι τόσο οι γεννήσεις όσο και οι θάνατοι είναι ανεξάρτητοι του μεγέθους του πληθυσμού. Αυτό, όπως και στο συνεχές μοντέλο, είναι προβληματικό καθώς ο πληθυσμός δεν μπορεί να αυξάνει επ’ άπειρον!

5.3.2 Διακριτό Λογιστικό Μοντέλο

Για την «βελτίωση» του παραπάνω μοντέλου, αντίστοιχη με αυτή του συνεχούς μοντέλου, χρειαζόμαστε ένα κατά κεφαλή ρυθμό μεταβολής, ο οποίος να είναι ανάλογος του πληθυσμού, δηλαδή:

\frac{\Delta P}{P}=F(P),

όπου $F(P)$ είναι μια δεδομένη συνάρτηση. Μια πρώτη επέκταση του διακριτού γραμμικού (Μαλθουσιανού) μοντέλου είναι το διακριτό λογιστικό μοντέλο. Η μορφή του είναι:

\frac{\Delta P}{P}=r\left(1-\frac{P}{K}\right)\Rightarrow P_{t+1}=P_{t}\left[1% +r\left(1-\frac{P_{t}}{K}\right)\right]

(5.16)

όπου $K$ και $r$ είναι, όπως και στο συνεχές Λογιστικό μοντέλο, αντίστοιχα η χωρητικότητα του περιβάλλοντος και ο (διακριτός) ρυθμός μεταβολής του πληθυσμού. Όπως βλέπουμε από την παραπάνω εξίσωση περιμένουμε σε μεγάλους χρόνους ο πληθυσμός να πλησιάζει την τιμή $K$ καθώς το δεξί μέλος της εξίσωσης γίνεται μονάδα.

Αν και αρκετά απλό το διακριτό λογιστικό μοντέλο δεν έχει γενική λύση για το $P_{t}$ συναρτήσει της αρχικής τιμής $P_{0}$ και των σταθερών $r$ και $K$ . Αυτό σημαίνει ότι ο μόνος τρόπος επίλυσης είναι ο επαναληπτικός υπολογισμός, δηλαδή για να βρούμε το $P_{100}$ πρέπει να κάνουμε 100 επαναλήψεις! Για το λόγο αυτό η «επίλυση» αυτού, αλλά και των περισσότερων διακριτών μοντέλων, γίνεται με χρήση υπολογιστή. Στη περίπτωσή μας η επίλυση του μοντέλου έχει γίνει με κώδικα σε γλώσσα MATLAB, ο οποίος βρίσκεται στο τέλος του κεφαλαίου.

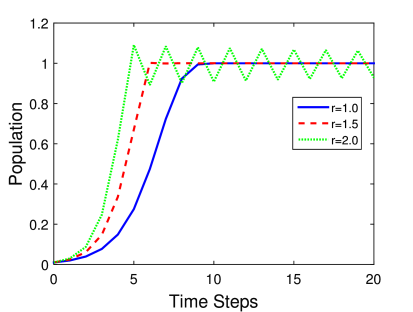
Η γραφική παράσταση του παραπάνω μοντέλου για ένα συγκεκριμένο παράδειγμα φαίνεται στο Σχήμα 5.4. Πιο συγκεκριμένα βλέπουμε την χρονική εξέλιξη του πληθυσμού για τρεις διαφορετικούς ρυθμούς ανάπτυξης. Σε κάθε περίπτωση θεωρούμε χωρητικότητα $K=1$ (ο πληθυσμός έχει κανονικοποιηθεί με την χωρητικότητα) και ο αρχικός πληθυσμός είναι $P_{0}=0.01$ . Προσέξτε ότι αν ο αρχικός πληθυσμός είναι μηδέν δεν υπάρχει εξέλιξη του πληθυσμού, παραμένει δηλαδή πάντα μηδέν!

Επίσης βλέπουμε ότι η συμπεριφορά του μοντέλου για μεγάλους ρυθμούς ανάπτυξης σε μεγάλους χρόνους γίνεται περιοδική. Αυτό είναι μια «εγγενής» ιδιαιτερότητα η οποία προκύπτει λόγω της ασυνέχειας του πληθυσμού, καθώς όπως είδαμε δεν εμφανίζεται σε καμία περίπτωση στο συνεχές λογιστικό μοντέλο. Σε ακόμη μεγαλύτερους ρυθμούς ανάπτυξης η συμπεριφορά του μοντέλου γίνεται χαοτική όπως θα δούμε παρακάτω.

Ερώτηση κατανόησης 5.10.

Τι συμβαίνει αν αλλάξουμε τον αρχικό πληθυσμό; Τι συμβαίνει αν αυξήσουμε παραπάνω τον ρυθμό αύξησης; Δοκιμάστε μόνοι σας.

Σχήμα 5.4: Χρονική εξέλιξη ενός πληθυσμού που ακολουθεί το διακριτό Λογιστικό μοντέλο για διαφορετικούς ρυθμούς ανάπτυξης. Σε κάθε περίπτωση ο αρχικός πληθυσμός είναι και $P_{0}=0.01$ και η χωρητικότητα $K=1$ .

Παρακάτω εξετάζουμε με μεγαλύτερη λεπτομέρεια την συμπεριφορά του πληθυσμού σε μεγάλους χρόνους, δηλαδή την κατάσταση ισορροπίας (αν υπάρχει) όπως περιγράφεται από το διακριτό λογιστικού μοντέλου.

Ανάλυση Μη-γραμμικών Διακριτών Μοντέλων: Χαοτική Συμπεριφορά

Έστω $P^{*}$ το σημείο ισορροπίας, ή καλύτερα για διακριτή μεταβλητή η τιμή ισορροπίας, Τ.Ι., (equilibrium value), για ένα μη-γραμμικό διακριτό μοντέλο, της μορφής: $P_{t+1}=F(P_{t})$ . Η ανάλυση ευστάθειας γίνεται όπως και στα συνεχή μοντέλα (δες παραπάνω και Κεφάλαιο 3).

Αρχικά θα δώσουμε μια γενική περιγραφή σε αναλογία με την περίπτωση των συνεχών μοντέλων. Η Τ.Ι. ορίζεται ως η τιμή του πληθυσμού $P^{*}$ για την οποία: $P^{*}=F(P^{*})$ . Έστω μια διαταραχή $\epsilon$ γύρω από την Τ.Ι., τότε θεωρώντας γραμμική μεταβολή (γραμμικοποίηση) για την τιμή του πληθυσμού, αυτή σε γίνεται

P_{t}=P^{*}+\epsilon_{t}

στο βήμα $t$ , και

P_{t+1}=P^{*}+\epsilon_{t+1}

στο βήμα $t+1$ . Από τις δύο παραπάνω σχέσεις, εύκολα βλέπουμε ότι

\frac{\epsilon_{t+1}}{\epsilon_{t}}=\frac{P_{t+1}-P^{*}}{P_{t}-P^{*}}=\frac{F(% P_{t})-F(P^{*})}{P_{t}-P^{*}}

από τον ορισμό της Τ.Ι. Στο όριο που το $P_{t}\to P^{*}$ μπορούμε να ορίσουμε μια προσεγγιστική «παράγωγος» τη μορφής:

F^{\prime}(P^{*}):=\lim_{P_{t}\to P^{*}}⁡\frac{F(P_{t})-F(P^{*})}{P_{t}-P^{*}}

Για την μελέτη ευστάθειας, και με βάση τους παραπάνω ορισμούς, χρησιμοποιούμε το παρακάτω θεώρημα.

Θεώρημα.

Αν ένα διακριτό μοντέλο της μορφής $P_{t+1}=F(P_{t})$ έχει Τ.Ι. $P^{*}$ τότε

•

Αν $|F^{\prime}(P^{*})|<1$ : το σημείο είναι ευσταθές.
•

Αν $|F^{\prime}(P^{*})|>1$ : το σημείο είναι ασταθές.
•

Αν $|F^{\prime}(P^{*})|=1$ : δεν μπορούμε να προσδιορίσουμε την ευστάθεια.

Επιστρέφοντας στο διακριτό λογιστικό μοντέλο που είδαμε παραπάνω, οι τιμές ισορροπίας του μοντέλου είναι: $P^{*}=0$ ή $P^{*}=K$ .

Κατόπιν, γραμμικοποίηση του μοντέλου αυτού θα μας δώσει:

F^{\prime}(P)=\left(1+r-\frac{2rP_{t}}{K}\right)\,.

(5.17)

Συνεπώς έχουμε:

•

$P^{*}=0$ . Το σημείο είναι πάντα ασταθές (εφόσον $r>0$ ).
•

$P^{*}=K$ . Αν $|1-r|<1$ : το σημείο είναι ευσταθές. Αν $|1-r|>1$ : το σημείο είναι ασταθές.

Βλέπουμε ότι το σημείο $P^{*}=K$ έχει ιδιαίτερο ενδιαφέρον, καθώς

•

Αν $0<1–r<1$ : το σημείο είναι ευσταθές.
•

Αν $1<r<2$ : το σημείο είναι ευσταθές αλλά το πρόσημο της διαταραχής εναλλάσσεται όσο ο χρόνος αυξάνει. Δηλαδή ο πληθυσμός φτάνει στην Τ.Ι. με ταλάντωση.
•

Αν $r>2$ : Ο πληθυσμός δεν έχει Τ.Ι. Το σημείο είναι ασταθές.
•

Αν το $r$ είναι αρκετά μεγάλο ο πληθυσμός δεν φτάνει σε ισορροπία, και ταυτόχρονα δεν μεταβάλλεται μονότονα. Εμφανίζει δηλαδή μη προβλέψιμη (χαοτική) συμπεριφορά.

Ερώτηση κατανόησης 5.11.

Πως συγκρίνεται η παραπάνω συμπεριφορά με το συνεχές λογιστικό μοντέλο;

Η γραφική παράσταση της χαοτικής συμπεριφοράς φαίνεται στα Σχήματα 5.5 και 5.6. Αρχικά στο Σχήμα 5.5 εμφανίζεται η συμπεριφορά του μοντέλου για ρυθμούς ανάπτυξης μεγαλύτερους από αυτούς που είδαμε στο προηγούμενο κεφάλαιο. Η συμπεριφορά στους μεγάλους χρόνους είναι περιοδική, ωστόσο όσο μεγαλώνει ο ρυθμός αύξησης r γίνεται μη προβλέψιμος. Αυτή είναι μια τυπική συμπεριφορά χαοτικού δυναμικού συστήματος (ντετερμινιστικό χάος, deterministic chaos) όπως είδαμε και στα Δυναμικά συστήματα (Κεφάλαιο 3).

Σχήμα 5.5: Χρονική εξέλιξη ενός πληθυσμού που ακολουθεί το διακριτό Λογιστικό μοντέλο για σχετικά μεγάλους ρυθμούς ανάπτυξης. Σε κάθε περίπτωση ο αρχικός πληθυσμός είναι και $P_{0}=0.01$ και η χωρητικότητα $K=1$ .

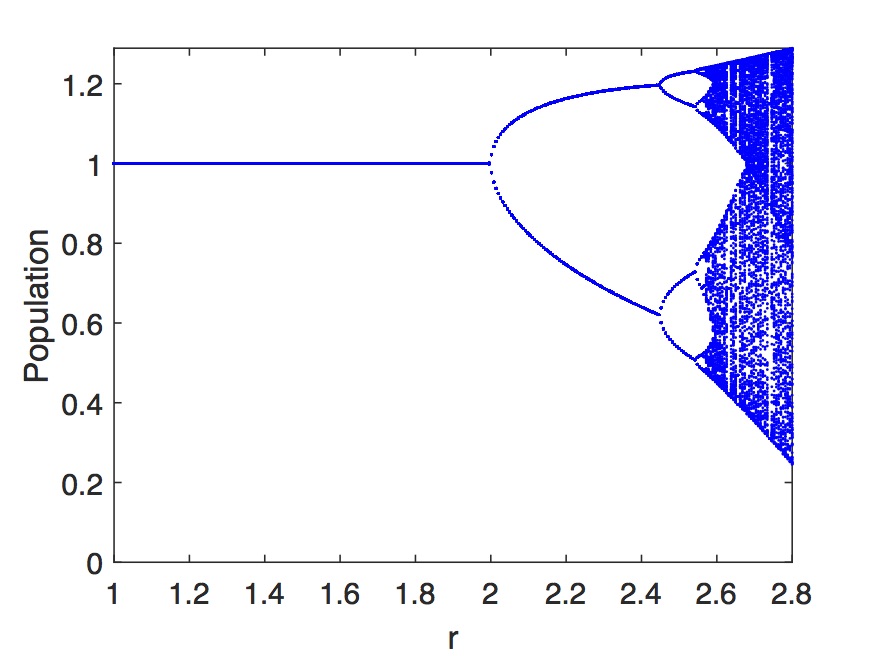
Κατόπιν στο Σχήμα 5.6 εμφανίζεται το διάγραμμα διακλάδωσης (bifurcation diagram) για έναν πληθυσμό που περιγράφεται με το διακριτό λογιστικό μοντέλο. Το διάγραμμα διακλάδωσης είναι μια γραφική παράσταση με όλες τις τιμές ισορροπίας $P_{t}$ για δεδομένο $r$ . Πρακτικά προκύπτει κρατώντας όλες τις τιμές του πληθυσμού $P_{t}$ για μεγάλους χρόνους $t$ , εξαιρώντας δηλαδή τις αρχικές τιμές. Συνήθως το δείχνουμε ως πυκνότητα πληθυσμού (population density), $P_{t}/K$ vs. $r$ . Όπως βλέπουμε για μικρούς ρυθμούς αύξησης $r$ υπάρχει μόνο μια σταθερή τιμή του πληθυσμού. Για μεγαλύτερες τιμες του $r$ αρχίζουν να εμφανίζονται δυο σταθερές τιμές (κύκλος δύο τιμών). Για ακόμη μεγαλύτερες τιμές του ρυθμού $r$ οι τιμές γίνονται 4 (κύκλος τεσσάρων τιμών) κ.ο.κ. Σε κάθε πρίπτωση ο κύκλος $2n+1$ είναι μικρότερος σε εύρος των $r$ από τον $2n$ . Για μια δεδομένη τιμή του $r(r\eqsim 2.692\ldots)$ όλοι οι πιθανοί κύκλοι έχουν ενεργοποιηθεί και η τιμή του $P_{t}$ (ή $P_{t}/K$ ) γίνεται τυχαία – χαοτική («ντετερμινιστικό χάος»).

Σχήμα 5.6: Διάγραμμα διακλάδωσης ενός πληθυσμού που ακολουθεί το διακριτό Λογιστικό μοντέλο.

Η παραπάνω συμπεριφορά έχει, πέρα από το μαθηματικό και τεράστιο βιολογικό ενδιαφέρον, καθώς αποδεικνύει ότι πολύπλοκη δυναμική εξέλιξη ενός απομονωμένου πληθυσμού, μπορεί να προέλθει ακόμη και χωρίς καμία αλλαγή στο περιβάλλον! Επίσης εξηγεί την περιοδική συμπεριφορά που εμφανίζουν βιολογικά είδη (π.χ. πληθυσμοί ψαριών) ακόμη και σε απομονωμένα ή ελεγχόμενα οικοσυστήματα. Περισσότερες πληροφορίες για μελέτη συστημάτων που εμφανίζουν χαοτική συμπεριφορά μπορούν να βρεθούν σε πιο εξειδικευμένα συγγράμματα. [35]

5.3.3 Παράδειγμα: Διακριτό Μοντέλο Ανάπτυξης Καρκινικών Κυττάρων

Ώ παράδειγμα, εδώ θα δούμε ένα διακριτό μοντέλο για την μελέτη του πληθυσμού (ανάπτυξη) καρκινικών κυττάρων το οποίο έχει προταθεί από τους S. Cross and D. Cotton το 1994 [S.S. Cross and D.W.K. Cotton. Chaos and antichaos in pathology. Human Pathol., 25:630–637, 1994].

Στο μοντέλο αυτό θεωρούμε το ποσοστό καρκινικών κυττάρων $P_{t}$ , ως προς το σύνολο όλων των κυττάρων, το οποίο στη διακριτή χρονική στιγμή t δίνεται από την εξίσωσή:

P_{t+1}=rP_{t}[1-P_{t}]=F(P)

(5.18)

όπου $r$ είναι ο ρυθμός αύξησης των καρκινικών κυττάρων. Προσέξτε ότι η μορφή του μοντέλου είναι αρκετά παρόμοια, αλλά όχι ακριβώς ίδια, με αυτή του διακριτού Λογιστικού μοντέλου.

Προσέξτε ότι για να μην υπάρχει μείωση του πληθυσμού πρέπει και πάλι $r>1$ . Επίσης ως ποσοστό πληθυσμού, πρέπει: $0.0\leq P_{t}\leq 1.0$ .

Παρακάτω μελετούμε την ευστάθεια του μοντέλου. Αρχικά υπολογίζουμε την τιμή ισορροπίας, $P^{*}$ , η οποία είναι:

P_{t+1}=F(P_{t})|_{P_{t}=P^{*}}=P_{t}\Rightarrow r(1-P^{*})=1\Rightarrow P^{*}% =\frac{r-1}{r}\,.

Όπως βλέπουμε η T.I. εξαρτάται από το ρυθμό $r$ . Η ανάλυση ευστάθειας για την τιμή ισορροπίας στο συγκεκριμένο μοντέλο δίνει:

f^{\prime}(P)=r-2rP(t)\Rightarrow f^{\prime}(P_{t})|_{P_{t}=P^{*}}=r-2(r-1)=2-r.

Συνεπώς:

•

Αν $|F^{\prime}(P)|<1$ ή $r<3$ : το σημείο είναι ευσταθές.
•

Αν $|F^{\prime}(P)|>1$ ή $r>3$ : το σημείο είναι ασταθές.

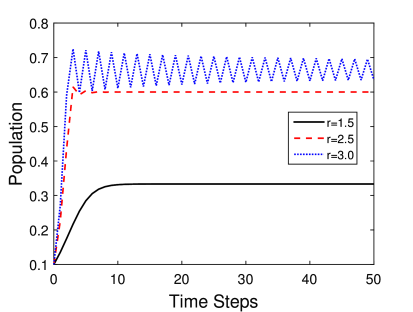
Σχήμα 5.7: Χρονική εξέλιξη ενός πληθυσμού που ακολουθεί το διακριτό μοντέλο για την ανάπτυξη των καρκινικών κυττάρων για διαφορετικούς ρυθμούς ανάπτυξης. Ο αρχικός πληθυσμός είναι σε κάθε περίπτωση $P_{0}=0.1$ .

Παράδειγμα χρονικής εξέλιξης ενός πληθυσμού ανάπτυξης καρκινικών κυττάρων που ακολουθεί το παραπάνω διακριτό μοντέλο φαίνεται στα Σχήματα 5.7α και 5.7β. Πιο συγκεκριμένα στο Σχήμα 5.7α βλέπουμε την μεταβολή του πληθυσμού για μικρές και στο Σχήμα 5.7β για μεγαλύτερες τιμές του ρυθμού ανάπτυξης. Παρατηρήστε τις διαφορές.