5.2 Συνεχή Πληθυσμιακά Μοντέλα Ενός Είδους
Όπως αναφέραμε και παραπάνω ένα βιολογικό πρόβλημα, με ιδιαίτερο πρακτικό ενδιαφέρον, αφορά τη χρονική εξέλιξη του πληθυσμού ενός ή περισσοτέρων βιολογικών ειδών, π.χ. πουλιών, ψαριών κλπ, σε κάποιο δεδομένο, ελεγχόμενο ή μη, περιβάλλον. Τα πληθυσμιακά μοντέλα μελετούν ακριβώς τέτοιου τύπου προβλήματα. Ειδικότερα τα πληθυσμιακά μοντέλα ενός είδους περιγράφουν την χρονική εξέλιξη του συγκεκριμένου είδους, χωρίς να θεωρούν ότι υπάρχει κάποιο άλλο είδος στο συγκεκριμένο οικοσύστημα το οποίο να επηρεάζει τον πληθυσμού του είδους που μας ενδιαφέρει.
Ερώτηση κατανόησης 5.2.
Δώστε παραδείγματα βιολογικών συστημάτων τα οποία περιγράφονται με μοντέλα πληθυσμού ενός είδους; Δικαιολογήστε την απάντησή σας.
Τα μοντέλα πληθυσμών ενός είδους σχετίζονται, δηλαδή μπορούν να περιγράψουν με σχετικά καλή ακρίβεια, με περιβάλλοντα (βιολογικές συνθήκες) τα οποία είτε είναι αρκετά ελεγχόμενα (π.χ. στο εργαστήριο ή σε μονάδες καλλιέργειας), είτε είναι απομονωμένα (π.χ. νησιά) στα οποία δεν υπάρχουν φυσικοί εχθροί για το υπό μελέτη είδος. Επιπλέον όμως τα μοντέλα πληθυσμών ενός είδους μπορούν να δώσουν μια πρώτη προσέγγιση πραγματικών πολύπλοκων οικοσυστημάτων.
Όπως είδαμε και παραπάνω τα μοντέλα πληθυσμών ενός είδους, αλλά και γενικότερα τα μαθηματικά μοντέλα στη βιολογία μπορούν να χωριστούν σε συνεχή και διακριτά ανάλογα με το είδος των μαθηματικών αναπαραστάσεων που χρησιμοποιούν. Θα πρέπει εδώ να σημειώσουμε:
-
1.
Στη μελέτη των συνεχών μοντέλων (συνήθεις διαφορικές εξισώσεις) έχουμε το πλεονέκτημα της χρήσης αναλυτικών εργαλείων (βλέπε τη γενικότερη συζήτηση που αφορά τα Δυναμικά Συστήματα, Κεφάλαιο 3).
-
2.
Με βάση τις πραγματικές συνθήκες θα περιμέναμε τα διακριτά μοντέλα να είναι πιο κοντά στη πραγματικότητα, καθώς: (α) ο πληθυσμός ενός είδους είναι διακριτή (ακέραια) μεταβλητή, και (β) η αναπαραγωγή των ειδών γίνεται σε διακριτές χρονικές περιόδους (π.χ. διάρκεια εγκυμοσύνης θηλυκών ενός είδους). Αν όμως θεωρήσουμε: (α) μεγάλους αριθμούς ατόμων του είδους και (β) ότι η χρονική περίοδος την οποία μελετάμε είναι αρκετά μεγαλύτερη από την αντίστοιχη περίοδο αναπαραγωγής μπορούμε να θεωρήσουμε ότι η συνεχής περιγραφή είναι μια καλή προσέγγιση. Σε αυτή την περίπτωση μπορούμε να χρησιμοποιήσουμε βασικά εργαλεία συνεχών συναρτήσεων και διαφορικών εξισώσεων. Αντίθετα η επίλυση των διακριτών μοντέλων γίνεται συνήθως με αριθμητικούς τρόπους.
Λόγω της παραπάνω «ευκολίας» των συνεχών μοντέλων, περιγράφουμε πρώτα αυτά, ενώ κατόπιν βλέπουμε τα αντίστοιχα διακριτά μοντέλα.
5.2.1 Μαλθουσιανό – Εκθετικό Μοντέλο
Στην αρχή αυτού του κεφαλαίου είδαμε ήδη, ως ένα πρώτο παράδειγμα, το απλούστερο δυνατό συνεχές μαθηματικό μοντέλο πληθυσμού ενός είδους, το οποίο ονομάζεται εκθετικό ή Μαλθουσιανό, καθώς όπως είδαμε καταλήγει σε εκθετική εξέλιξη του πληθυσμού. Το μοντέλο αυτό αναπτύχθηκε από τον Malthus το 1798, ο οποίος μελετούσε την αύξηση του ανθρώπινου πληθυσμού, είναι δηλαδή το πρώτο δημογραφικό μοντέλο. Η γενική του μορφή είναι η παρακάτω.
Θεωρούμε ένα συγκεκριμένο οικοσύστημα (π.χ. λίμνη, δάσος, νησί, χώρα κλπ.). Έστω ο πληθυσμός ενός είδους (π.χ. ψάρι, πουλί, ζώο, άνθρωπος, κλπ.) σε χρόνο . Θεωρώντας ότι δεν υπάρχουν φυσικοί εχθροί για το είδος και υπάρχει «άπειρο» διαθέσιμο φαγητό ο ρυθμός μεταβολής του πληθυσμού εξαρτάται από το ρυθμό γεννήσεων και θανάτων, δηλαδή γίνεται:
| (5.4) |
Ο τελευταίος όρος περιγράφει τις αλλαγές (αύξηση ή μείωση) του πληθυσμού λόγω μετακίνησης κάποιων ατόμων του πληθυσμού σε άλλα μέρη. Κάνουμε τις παρακάτω υποθέσεις:
-
•
Οι γεννήσεις (καλύτερα ο ρυθμός γεννήσεων) περιγράφονται με ένα γραμμικό όρο, ως προς τον αριθμό του πληθυσμού , δηλαδή με ένα όρο , όπου (birth) είναι μια θετική σταθερά,
-
•
Ο ρυθμός θανάτων περιγράφεται επίσης με ένα γραμμικό όρο, ως προς τον αριθμό του πληθυσμού , δηλαδή με ένα όρο , όπου (death) είναι μια θετική σταθερά, .
-
•
Η μετανάστευση δεν συνεισφέρει στην εξέλιξη του πληθυσμού, δηλαδή ο ρυθμός εισαγωγής ατόμων του είδους στο οικοσύστημα είναι ίσος με τον ρυθμό εξαγωγής.
Τότε, ορίζοντας τον ρυθμό αύξησης (rate), ως η μορφή του μοντέλου, εξίσωση (5.4), γίνεται:
| (5.5) |
Η παραπάνω διαφορική εξίσωση μαζί με μια αρχική συνθήκη (τιμή του πληθυσμού σε μια αρχική χρονική στιγμή) αποτελεί ένα πρόβλημα αρχικών τιμών, Π.Α.Τ., το οποίο περιγράφει το Μαλθουσιανό ή εκθετικό μοντέλο. Η λύση αυτού του Π.Α.Τ. είναι, όπως είδαμε και παραπάνω:
| (5.6) |
όπου είναι η αρχική τιμή του πληθυσμού.
Παρατήρηση 5.3.
Προσέξτε ότι στην παραπάνω εξίσωση οι μονάδες των σταθερών και είναι [].
Ορισμός.
Ο κατά κεφαλήν ρυθμός μεταβολής r ορίζεται ως: .
Ο κατά κεφαλήν ρυθμός μεταβολής είναι ένα μέτρο δυναμικής-κινητικής του πληθυσμού. Αν υπάρχει εκθετική αύξηση του πληθυσμού, ενώ αν , υπάρχει εκθετική μείωση του πληθυσμού.
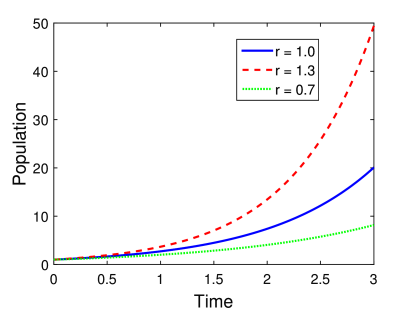
Η γραφική αναπαράσταση της εξίσωσης (5.6) φαίνεται στο Σχήμα 5.1 για διαφορετικές τιμές των παραμέτρων, και πιο συγκεκριμένα του ρυθμού αύξησης . Σε όλες τις περιπτώσεις η αρχική τιμή του πληθυσμού είναι 1.0.
Όπως βλέπουμε στο γράφημα 5.1, κάτω από τις αρχικές υποθέσεις που έχουμε κάνει, το Μαλθουσιανό μοντέλο προβλέπει συνεχή – εκθετική αύξηση του πληθυσμού ενός συγκεκριμένου βιολογικού είδους. Επίσης παρατηρούμε την ιδιαίτερα ισχυρή επίδραση της σταθεράς : μικρή αύξηση του ρυθμού οδηγεί σε μεγάλη αύξηση του πληθυσμού [38].
Ερώτηση κατανόησης 5.3.
Είναι το παραπάνω μοντέλο ρεαλιστικό;
Εξίσωση του Gompertz
Μία επέκταση του εκθετικού μοντέλου επιχειρήθηκε από τον Benjamin Gompertz το 1825 για να περιγράψει το ρυθμό μεταβολής του πληθυσμού των ανθρώπων πιο ρεαλιστικά από το Μαλθουσιανό μοντέλο, λαμβάνοντας υπόψιν τη θνησιμότητα (B. Gompertz, ”On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies.” Phil. Trans. Roy. Soc. London 123, 513-585, 1825). [40].
Ο Gompertz προσπάθησε να βελτιώσει το δημογραφικό μοντέλο του Μάλθους χρησιμοποιώντας δεδομένα (χρονοσειρές) θνησιμότητας. Το αρχικό του μοντέλο βασίζεται στην υπόθεση ότι η «αντίσταση» στη θνησιμότητα ενός ατόμου μειώνεται όσο αυξάνεται η ηλικία του. Η εξίσωση (ή το μοντέλο) του Gompertz έχει την παρακάτω μορφή:
| (5.7) |
όπου είναι ο πληθυσμός (αριθμός των ατόμων) σε χρόνο 0, ενώ είναι σταθερές. Το παραπάνω μοντέλο χρησιμοποιήθηκε εκτενώς από τις ασφαλιστικές εταιρείες για τον υπολογισμό του κόστους ασφάλισης ενός ατόμου συναρτήσει της ηλικίας του.
5.2.2 Λογιστικό Μοντέλο
Εύκολα καταλαβαίνουμε ότι το εκθετικό μοντέλο που παρουσιάσθηκε παραπάνω, ακόμη και αν είναι ακριβές για κάποια χρονική περίοδο, δεν μπορεί να ισχύει για πολύ μεγάλα χρονικά διαστήματα. Περιμένουμε λοιπόν για το υπό μελέτη σύστημα να υπάρχει κάποια τροποποίηση της εκθετικής συμπεριφοράς και σε μεγάλους χρόνους ο πληθυσμός του είδους να σταθεροποιείται, δηλαδή ο ρυθμός μεταβολής του πληθυσμού να τείνει στο μηδέν.
Μία εξίσωση που έχει την παραπάνω ιδιότητα προτάθηκε από τον Pierre Verhulst το 1838 και ονομάζεται λογιστική ανάπτυξη (logistic growth), ή αλλιώς η εξίσωση του Verhulst [Verhulst, Pierre-François (1838). ”Notice sur la loi que la population suit dans son accroissement”. Correspondance mathématique et physique 10: 113–121]. Ο Verhulst μελετούσε την εξέλιξη του πληθυσμού των ανθρώπων και στην προσπάθειά του να βελτιώσει το Μαλθουσιανό μοντέλο πρότεινε την παρακάτω εξίσωση:
| (5.8) |
όπου είναι μια θετική σταθερά η οποία ονομάζεται χωρητικότητα του περιβάλλοντος και είναι μια σταθερά, η οποία περιγράφει, όπως και παραπάνω, το ρυθμό αύξησης του πληθυσμού. Η δε παράμετρος μπορεί να κατανοηθεί ως ο χαρακτηριστικός χρόνος απόκρισης του συστήματος σε μεταβολές του πληθυσμού.
Ο κατά κεφαλή ρυθμός μεταβολής, ορίζεται ως:
| (5.9) |
Ερώτηση κατανόησης 5.4.
Ποια είναι η φυσική σημασία του κατά κεφαλή ρυθμού μεταβολής; Ποιο είναι το πρόσημό του αν: (α) και (β) ;
Η χωρητικότητα μας δίνει το μέγιστο αποδεκτό σταθερό (χρόνο-ανεξάρτητο) πληθυσμό για ένα είδος και εξαρτάται από τις συνθήκες του περιβάλλοντος. Ας μελετήσουμε την παραπάνω εξίσωση, εξετάζοντας πρώτα τα σημεία ισορροπίας (Σ.Ι.) της και την ευστάθειάς τους (δες επίσης Κεφάλαιο 3). Για να το επιτύχουμε ορίζουμε τη συνάρτηση :
| (5.10) |
Προσέξτε ότι η μελέτη ευστάθειας των Σ.Ι., πέρα από το μαθηματικό ενδιαφέρον, είναι ιδιαίτερα σημαντική και από βιολογικής απόψεως καθώς μας δίνει πληροφορίες για τη συμπεριφορά της μεταβλητής (εδώ πληθυσμού) γύρω από συγκεκριμένες τιμές. Ασταθές Σ.Ι. σημαίνει ότι ξεκινώντας από πληθυσμό με αυτές τις τιμές, μια μικρή αλλαγή (διαταραχή) του πληθυσμού θα τον οδηγήσει σε μεγάλους χρόνους μακριά από την αρχική του τιμή. Αντίθετα ευσταθές Σ.Ι. σημαίνει ότι ο πληθυσμός, αν βρεθεί σε αυτή την τιμή, θα τείνει να παραμείνει εκεί για όλους τους χρόνους.
Τα σημεία ισορροπίας, όπως έχουμε δει, ορίζονται ως οι τιμές της μεταβλητής (του πληθυσμού) για τις οποίες η συνάρτηση , δηλαδή η παράγωγος , είναι μηδέν. Στη λογιστική εξίσωση αυτά τα σημεία είναι τα:
-
(α)
και
-
(β)
.
Η μελέτη ευστάθειας των παραπάνω Σ.Ι. γίνεται, όπως είδαμε και σε προηγούμενο κεφάλαιο, θεωρώντας μια μικρή αλλαγή (διαταραχή) του πληθυσμού ε γύρω από ένα σημείο , με αντίστοιχη γραμμικοποίηση (ανάπτυγμα Taylor και κράτημα όρων μέχρι πρώτης τάξης), η οποία θα μας δώσει:
Για το λογιστικό μοντέλο: .
Η παραπάνω εξίσωση για τα δύο σημεία ισορροπίας (Σ.Ι.) δίνει:
-
•
. Σε αυτή την περίπτωση ο ρυθμός μεταβολής της διαταραχής μέσω της παραπάνω σχέσης γίνεται:
Η λύση της παραπάνω εξίσωσης, για μια δεδομένη αρχική τιμή της διαταραχής, , είναι:
Βλέπουμε ότι, για θετικό , η διαταραχή αυξάνεται εκθετικά, οπότε το Σ.Ι. είναι ασταθές. Συνεπώς αν ο αρχικός πληθυσμός δεν είναι ακριβώς μηδέν θα αρχίσει να αυξάνεται με το χρόνο. Αυτό είναι ιδιαίτερα σημαντικό καθώς επιτρέπει την αύξηση του πληθυσμού, όπως και θα περιμέναμε από την εμπειρία μας σε πραγματικά βιολογικά συστήματα.
-
•
. Σε αυτή την περίπτωση ο ρυθμός μεταβολής της διαταραχής γίνεται:
Η λύση τώρα της εξίσωσης είναι:
Εφόσον ο ρυθμός αύξησης είναι , η διαταραχή μειώνεται εκθετικά, οπότε το Σ.Ι. είναι ευσταθές. Συνεπώς αν ο αρχικός πληθυσμός φτάσει κάποια στιγμή στην τιμή , θα παραμείνει εκεί και θα είναι ανεξάρτητος του χρόνου!
Συμπερασματικά, βλέπουμε λοιπόν ότι πρακτικά περιμένουμε ο πληθυσμός σε μεγάλους χρόνους να τείνει προς το δεύτερο (ευσταθές) σημείο ισορροπίας, .
Στο επόμενο στάδιο εξετάζουμε αν η αρχική διαφορική εξίσωση έχει αναλυτική λύση. Αυτό ισχύει (η εύρεσή της αφήνεται ως άσκηση στον αναγνώστη) και, για , είναι:
| (5.11) |
Η παραπάνω σχέση, όπως περιμένουμε, στο όριο του δίνει .
Σύντομο πρόβλημα 5.2.
Επιβεβαιώστε ότι η παραπάνω εξίσωση είναι λύση του αρχικού Π.Α.Τ.
Η γραφική αναπαράσταση της παραπάνω εξίσωσης φαίνεται στο Σχήμα 5.2 για διαφορετικές τιμές των παραμέτρων. Πιο συγκεκριμένα εξετάζουμε δύο διαφορετικές περιπτώσεις μεταβάλλοντας τις τιμές του ρυθμού αύξησης και του αρχικού πληθυσμού.
Θεωρούμε σε όλες τις περιπτώσεις ότι . Προσέξτε ότι η εκλογή της τιμής της σταθεράς χωρητικότητας είναι μια τυπική περίπτωση που συνήθως εξετάζουμε σε κάθε μοντέλο, το οποίο εμπεριέχει χωρητικότητα. Πρακτικά σε αυτή την περίπτωση είναι σαν να εξετάζουμε τον πληθυσμό κάνοντας μια κανονικοποίηση με τη χωρητικότητα του οικοσυστήματος.
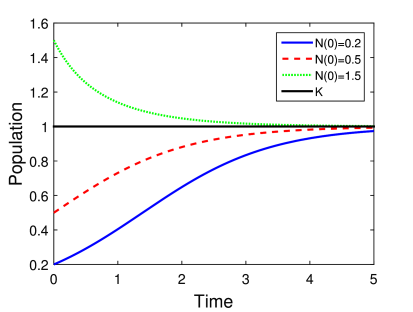
Στην πρώτη περίπτωση (Σχήμα 5.2α) θέτουμε και εξετάζουμε τη συμπεριφορά του πληθυσμού για διαφορετικές αρχικές τιμές . Όπως βλέπουμε σε όλες τις περιπτώσεις ο πληθυσμός προσεγγίζει «ομαλά» την μονάδα, δηλαδή ο αριθμός ατόμων του είδους τείνει σε μεγάλους χρόνους να γίνει, και να παραμείνει, ίσος με την χωρητικότητα του περιβάλλοντος.
Στη δεύτερη περίπτωση (Σχήμα 5.2β) θέτουμε και εξετάζουμε τη συμπεριφορά του πληθυσμού για διαφορετικές τιμές του ρυθμού αύξησης r. Όπως περιμένουμε πάλι ο πληθυσμός τείνει στη χωρητικότητα του περιβάλλοντος, ο ρυθμός, όμως με τον οποίο γίνεται αυτή η προσέγγιση είναι διαφορετικός για τις διαφορετικές τιμές του .
 |
 |
Το Λογιστικό μοντέλο είναι ίσως το πιο γνωστό πληθυσμιακό μοντέλο. Κύριο πλεονέκτημά του είναι η απλότητά του και βέβαια είναι πολύ πιο ρεαλιστικό από το Μαλθουσιανό μοντέλο. Ταυτόχρονα παρέχει μια πρώτη ιδέα για την ποιοτική συμπεριφορά της χρονικής εξέλιξης ενός απομονωμένου πληθυσμού ενός είδους.
Παρατήρηση 5.4.
Προσέξτε ότι για την εφαρμογή του μοντέλου σε ένα πραγματικό σύστημα, όπως και για κάθε άλλο μοντέλο, χρειαζόμαστε τιμές για τις σταθερές και . Οι τιμές αυτές βρίσκονται μέσα από στατιστικά δεδομένα – πειραματικές παρατηρήσεις που αφορούν ένα είδος. Κύρια πρακτική δυσκολία στην ακριβή εκτίμηση των σταθερών είναι ότι συνήθως υπάρχουν στατιστικά στοιχεία για μια συγκεκριμένη περίοδο για την οποία μπορεί μεν οι προβλέψεις του μοντέλου να είναι καλές (ακριβείς), αλλά μπορεί να μην είναι καλές για μεγαλύτερα χρονικά διαστήματα.
Ένα πρώτο παράδειγμα εφαρμογής του λογιστικού μοντέλου δόθηκε από τον Pearl [1925] ο οποίος προσπάθησε να εκτιμήσει τον πληθυσμό των Ηνωμένων Πολιτειών (USA) μέχρι το 2000. Για να το πετύχει υπολόγισε τις σταθερές του λογιστικού μοντέλου, χρησιμοποιώντας στατιστικά (δημογραφικά) δεδομένα πληθυσμού για τα έτη 1790-1930. Οι προβλέψεις του μοντέλου, ενώ ήταν σε καλή συμφωνία για το διάστημα στο οποίο υπήρχαν στατιστικά δεδομένα, υποεκτιμούσαν, όπως φάνηκε αργότερα, σε μεγάλο βαθμό τον πληθυσμό [40]. Ο λόγος αυτής της «αποτυχίας» έγκειται, πολύ απλά, στο ότι στην πραγματικότητα το λογιστικό, όπως και όλα τα δημογραφικά μοντέλα, είναι ημί-εμπειρικό, και η χρήση του σε χρονικά διαστήματα για τα οποία δεν έχουμε δεδομένα είναι σε μεγάλο βαθμό προσεγγιστική.
Γενίκευση Λογιστικού Μοντέλου – Εξίσωση von Bertalanffy
Μία γενίκευση του Λογιστικού μοντέλου προτάθηκε από τον von Bertalanffy το 1938, ο οποίος χρησιμοποίησε δεδομένα από εργασίες σε πληθυσμούς ψαριών. Πιο συγκεκριμένα η μορφή της εξίσωσης von Bertalanffy (γενίκευση της Λογιστικής Εξίσωσης) είναι:
| (5.12) |
όπου είναι η τιμή του πληθυσμού σε χρόνο η τιμή σε μεγάλους (άπειρο) χρόνο και ο ρυθμός ανάπτυξης. Η παραπάνω εξίσωση είναι αυτή που χρησιμοποιείται στις μέρες μας περισσότερο από κάθε άλλη εξίσωση ανάπτυξης σε μελέτες ενός πληθυσμού, ειδικότερα σε πληθυσμούς ψαριών. Η λύση της παραπάνω εξίσωσης (αφήνεται ως άσκηση για τον αναγνώστη) είναι:
| (5.13) |
Η παράμετρος χρησιμοποιείται για να προσαρμόσει την εξίσωση για το αρχικό μέγεθος του πληθυσμού και ορίζεται ως η χρονική στιγμή, για την οποία ο πληθυσμός έχει μηδενική τιμή.
Η χρήση του παραπάνω μοντέλου, όπως και κάθε άλλου βιολογικού μοντέλου, σε ένα συγκεκριμένο σύστημα απαιτεί, όπως είδαμε και παραπάνω, την εύρεση των σταθερών του μοντέλου. Συνεπώς για το συγκεκριμένο μοντέλο απαιτείται η εύρεση 3 σταθερών ( και ). Αυτό επιτυγχάνεται συνήθως με μη-γραμμική προσαρμογή (non-linear regression) χρησιμοποιώντας βιολογικά δεδομένα από το υπό μελέτη σύστημα.
5.2.3 Παράδειγμα: Μοντέλο με Συγκομιδή (Αλιεία)
Ένα πολύ πρακτικό βιολογικό πρόβλημα αφορά τη μελέτη ειδών τα οποία εμφανίζουν συγκομιδή. Χαρακτηριστικό παράδειγμα αποτελεί ο πληθυσμός ψαριών τα οποία αλιεύουμε από μια ελεγχόμενη μονάδα καλλιέργειας. Για ένα τέτοιο οικοσύστημα θα περιμέναμε οι βασικές υποθέσεις του λογιστικού μοντέλου να ισχύουν, δηλαδή
-
α)
Το είδος σε αυτό το ελεγχόμενο περιβάλλον δεν έχει εχθρούς,
-
β)
Το φαγητό βρίσκεται σε «αφθονία», και
-
γ)
Τα περιβάλλον (η ιχθυοκαλλιέργεια) έχει μια συγκεκριμένη χωρητικότητα πληθυσμού.
Επιπλέον όμως από τα παραπάνω θα πρέπει να ληφθεί υπόψη το ότι ο πληθυσμός μειώνεται και λόγω της συγκομιδής ή αλιείας (harvesting). Αν ορίσουμε ως το ρυθμό μείωσης πληθυσμού, ανά μονάδα πληθυσμού και ανά μονάδα χρόνου, λόγω της συγκομιδής, και την απόδοση της συγκομιδής (harvesting yield) ανά μονάδα χρόνου, τότε το πρακτικό ερώτημα που θα έχει κάθε μονάδα καλλιέργειας τέτοιου είδους είναι το ποια είναι η καλύτερη (σταθερή) απόδοση συγκομιδής.
Με τον όρο της μείωσης του πληθυσμού λόγω συγκομιδής το λογιστικό μοντέλο γίνεται:
| (5.14) |
Το παραπάνω μοντέλο έχει δύο σημεία ισορροπίας: (όλες οι ακόλουθες γραμμές φαίνεται να ξεκινούν ως νέες παράγραφοι)
-
α)
Το βασικό , και
-
β)
Το .
Η απόδοση της συγκομιδής ορίζεται ως: . Βλέπουμε ότι αν:
-
•
τότε , οπότε μόνη σταθερή κατάσταση είναι το , δηλαδή ο πληθυσμός πεθαίνει.
-
•
τότε . Αυτή είναι βασική προϋπόθεση της συγκομιδής ώστε να μην εξαφανισθεί ο πληθυσμός. Αυτό έχει τεράστια βιολογική σημασία καθώς δίνει μια βασική συνθήκη η οποία θα πρέπει να τηρείται ώστε να μην κινδυνεύσει ο πληθυσμός. Χαρακτηριστικό παράδειγμα στο οποίο δεν τηρήθηκε η συνθήκη και κινδύνεψε άμεσα ο πληθυσμός του είδους με εξαφάνιση είναι η φαλαινοθηρία κατά τη δεκαετία του 1970.
Ξαναγυρνώντας στο αρχικό ερώτημα η μέγιστη απόδοση της μονάδας βρίσκεται υπολογίζοντας το σημείο στο οποίο η παράγωγος της απόδοσης, ως προς το ρυθμός αλίευσης Ε μηδενίζεται. Τελικά η μέγιστη απόδοση είναι:
Σύντομο πρόβλημα 5.3.
Αποδείξτε την παραπάνω σχέση.
Η δυναμική ανάλυση του μη βασικού Σ.Ι. μας δίνει: (όλες οι ακόλουθες γραμμές φαίνεται να ξεκινούν ως νέες παράγραφοι)
Όπου:
Άρα τελικά:
το οποίο οδηγεί σε ευστάθεια αν .
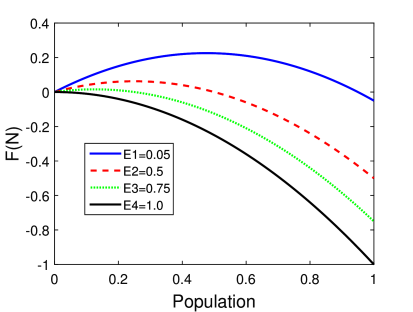
Η γραφική αναπαράσταση του ρυθμού μεταβολής του πληθυσμού, δηλαδή της συνάρτησης , για διαφορετικές τιμές του ρυθμού αλίευσης φαίνεται στο Σχήμα 5.3. Στο γράφημα αυτό η χωρητικότητα είναι 1, δηλαδή ο πληθυσμός παρουσιάζεται ως ποσοστό της χωρητικότητας. Όπως βλέπουμε για μεγάλους ρυθμούς αλίευσης (> 1 για τις τιμές του μοντέλου που εξετάζουμε εδώ) ο ρυθμός μεταβολής του πληθυσμού είναι αρνητικός για κάθε τιμή του πληθυσμού , πέρα από την αρχική τιμή για . Πρακτικά αυτό σημαίνει ότι το είδος θα εξαφανιστεί. Αντίθετα για μικρότερους ρυθμούς αλίευσης ο ρυθμός μεταβολής είναι αρχικά θετικός και κατόπιν γίνεται μηδενικός για μια τιμή του πληθυσμού. Δηλαδή υπάρχει «σταθερή» (χρονικά ανεξάρτητη) τιμή του πληθυσμού για συγκεκριμένο ρυθμό αλίευσης.