Σχεδίαση και Ανάλυση Αλγορίθμων 6 Αλγοριθμικές Τεχνικές 8 Αλγόριθμοι Ταξινόμησης

Κεφάλαιο 7Αλγόριθμοι Αναζήτησης

Από το αντικείμενο των Δομών Δεδομένων είναι γνωστή η μεγάλη σημασία του προβλήματος της αναζήτησης καθώς εμφανίζεται σε πλήθος θεωρητικών και πρακτικών προβλημάτων. Στο παρόν κεφάλαιο συνοψίζονται δεδομένα αποτελέσματα, αλλά παρουσιάζονται κατά αναλυτικότερο τρόπο.

7.1 Σειριακή Αναζήτηση

Η απλούστερη μέθοδος αναζήτησης είναι η σειριακή (sequential) ή αλλιώς γραμμική (linear). Αν και η μέθοδος είναι απολύτως γνωστή από το αντικείμενο των Δομών Δεδομένων, επαναλαμβάνουμε ελάχιστα σημεία ως εισαγωγή στο παρόν κεφάλαιο. Η επόμενη διαδικασία Sequential1 υποθέτει ότι αναζητείται η τιμή key στον πίνακα $A$ που περιέχει $n$ αταξινόμητα στοιχεία και επιστρέφει τη θέση του κλειδιού στον πίνακα ή την τιμή $-1$ , αν το κλειδί δεν υπάρχει (περίπτωση ανεπιτυχούς αναζήτησης).

Algorithm Sequential1(

k e y

)

i=1

2. while

(i\leq n)

3. if

A[i]==key

then return

i

4. else

i=i+1

5. return

-1

Σχήμα 7.1: Αλγόριθμος σειριακής αναζήτησης.

Η διαδικασία αυτή μπορεί να βελτιωθεί υιοθετώντας την τεχνική του κόμβου φρουρού (sentinel), οπότε η μέθοδος θα υλοποιηθεί θεωρώντας μία ακόμη θέση στον πίνακα με τη μορφή $A[n+1]<--key$ . Αν και πρακτικά η διαδικασία θα βελτιωθεί, σε θεωρητικό επίπεδο σε κάθε περίπτωση θα ισχύουν οι επόμενες προτάσεις υποθέτοντας ότι η πιθανότητα αναζήτησης του κλειδιού $A[i]$ είναι $p_{i}=1/n$ , για $1\leq i\leq n$ .

Πρόταση 7.1.

Η επιτυχής αναζήτηση σε πίνακα με $n$ αταξινόμητα κλειδιά έχει πολυπλοκότητα $\Theta(1)$ , $\Theta(n)$ και $\Theta(n)$ στην καλύτερη, στη χειρότερη και στη μέση περίπτωση, αντίστοιχα.

Απόδειξη. Η καλύτερη και η χειρότερη περίπτωση συμβαίνουν, όταν η αναζήτηση τερματίζεται με την εξέταση της πρώτης και της τελευταίας θέσης του πίνακα, αντίστοιχα. Για τη μέση περίπτωση ισχύει ότι:

\frac{1+2+...+n}{n}=\frac{n+1}{2}

από όπου προκύπτει η αλήθεια της πρότασης.

Πρόταση 7.2.

Η ανεπιτυχής αναζήτηση σε πίνακα με $n$ αταξινόμητα κλειδιά έχει πολυπλοκότητα $\Theta(n)$ στην καλύτερη, στη χειρότερη και στη μέση περίπτωση.

Απόδειξη. Σε κάθε περίπτωση θα σαρωθεί ολόκληρος ο πίνακας και, άρα, η πρόταση ισχύει.

Αν υποθέσουμε ότι ο πίνακας περιέχει $n$ ταξινομημένα στοιχεία, τότε για την επιτυχή αναζήτηση ισχύει η ανωτέρω πρόταση, αλλά για να επιταχύνουμε την ανεπιτυχή αναζήτηση πρέπει να μετατρέψουμε τη διαδικασία Sequential1 ως εξής:

Algorithm Sequential2(

k e y

)

done=FALSE

;

i=1

2. while

(i\leq n)

3. if

A[i]>key

then

i=i+1

4. else if

A[i]=key

then return

i

5. else return

-1

Σχήμα 7.2: Αλγόριθμος σειριακής αναζήτησης για ταξινομημένους πίνακες.

Πρόταση 7.3.

Η ανεπιτυχής αναζήτηση σε πίνακα με $n$ ταξινομημένα κλειδιά έχει πολυπλοκότητα $\Theta(1)$ , $\Theta(n)$ και $\Theta(n)$ στην καλύτερη, στη χειρότερη και στη μέση περίπτωση, αντίστοιχα.

Απόδειξη. Όταν αναζητούμε ένα μη υπαρκτό κλειδί, τότε αυτό μπορεί να ανήκει σε ένα από $n+1$ μεσοδιαστήματα που (σχηματικά) δημιουργούνται από τις τιμές των στοιχείων του πίνακα επάνω στην ευθεία των ακεραίων. Η καλύτερη και η χειρότερη περίπτωση συμβαίνουν, όταν το αναζητούμενο $k e y$ είναι μικρότερο από το πρώτο στοιχείο και μεγαλύτερο από το τελευταίο στοιχείο του πίνακα, αντίστοιχα. Για τη μέση περίπτωση θα πρέπει να εξετάσουμε $n+1$ περιπτώσεις και να λάβουμε το μέσο όρο τους. Αν το $k e y$ είναι μικρότερο από το πρώτο στοιχείο, τότε αρκεί μία σύγκριση για να τερματισθεί η διαδικασία. Αν το $k e y$ είναι μεγαλύτερο από το $i$ -οστό και μικρότερο από το $(i+1)$ -οστό στοιχείο (για $i<n$ ), τότε αρκούν $i+1$ συγκρίσεις. Αν το $k e y$ είναι μεγαλύτερο από το $n$ -οστό στοιχείο, τότε αρκούν $n$ συγκρίσεις. Συνεπώς, ισχύει:

\frac{1+2+...+n+n}{n+1}=\frac{1+2+...+n+n+1-1}{n+1}=\frac{n+2}{2}-\frac{1}{n+1}

από όπου προκύπτει η αλήθεια της πρότασης.

7.2 Δυαδική Αναζήτηση

Κλασικό παράδειγμα των αλγορίθμων της οικογενείας Διαίρει και Βασίλευε είναι η δυαδική αναζήτηση (binary search). Όπως γνωρίζουμε, η αναζήτηση αυτή εφαρμόζεται σε πίνακες που περιέχουν ταξινομημένα στοιχεία. Υπενθυμίζοντας όσα τονίσθηκαν στο Κεφάλαιο 4.2 σχετικά με την αποτελεσματικότητα των αναδρομικών και των επαναληπτικών μεθόδων, στη συνέχεια παρουσιάζουμε την επαναληπτική διαδικασία Binary_Iterate και την αναδρομική διαδικασία Binary_Rec που δείχνουν την ίδια θεωρητική συμπεριφορά.

Algorithm Binary_Iterate(

k e y

)

bottom=1

;

top=n

;

2. while

(bottom\leq top)

middle=(top+bottom)\div 2

4. if

A[middle]=key

then return

m i d d l e

5. else if

A[middle]>key

then

top=middle-1

6. else

bottom=middle+1

7. return

-1

Σχήμα 7.3: Επαναληπτικός αλγόριθμος δυαδικής αναζήτησης. Η

\div

αναπαριστά την ακέραια διαίρεση.

Algorithm Binary_Rec(

k e y, l e f t, r i g h t

)

1. if

left>right

then return

-1

;

middle=(top+bottom)\div 2

3. if

A[middle]=key

then return

m i d d l e

4. else if

A[middle]>key

then

5. Binary_Rec

(key,left,middle-1)

6. else Binary_Rec

(key,middle+1,right)

Σχήμα 7.4: Αναδρομικός αλγόριθμος δυαδικής αναζήτησης.

Μπορούμε να περιγράψουμε τη λογική των προηγούμενων διαδικασιών ως εξής: Έστω ότι αναζητούμε το ακέραιο κλειδί $k e y$ σε ένα πίνακα $A[1\ldots n]$ με ταξινομημένους ακεραίους αριθμούς. Συγκρίνουμε το κλειδί $k e y$ με το περιεχόμενο της μεσαίας θέσης του πίνακα $A$ , που είναι η θέση $m i d d l e$ . Στο σημείο αυτό τρία ενδεχόμενα μπορεί να συμβούν:

1.

τα δύο στοιχεία είναι ίσα, οπότε ο σκοπός μας επιτεύχθηκε,
2.

το $k e y$ είναι μικρότερο από το $A[middle]$ , οπότε είμαστε βέβαιοι ότι το $k e y$ αποκλείεται να βρίσκεται στον υποπίνακα $A[middle\ldots top]$ . Έτσι, συνεχίζουμε στον υποπίνακα $A[bottom\ldots middle-1]$ εξετάζοντας το μεσαίο στοιχείο του,
3.

το $k e y$ είναι μεγαλύτερο του $A[middle]$ , οπότε το $k e y$ σαφώς δεν βρίσκεται στον υποπίνακα $A[bottom\ldots middle]$ . Έτσι, συνεχίζουμε και πάλι εξετάζοντας το μεσαίο στοιχείο του υποπίνακα $A[middle+1\ldots top]$ .

Οι ανωτέρω διαδικασίες επιστρέφουν τη θέση του $k e y$ μέσα στον πίνακα. Αν το $k e y$ βρίσκεται πράγματι μέσα στον $A$ , τότε επιστρέφει τη συγκεκριμένη θέση, ενώ στην αντίθετη περίπτωση επιστρέφει την τιμή $-1$ . Ένα παράδειγμα εκτέλεσης του αλγορίθμου παρουσιάζεται στο Σχήμα 7.5.

Σχήμα 7.5: Παράδειγμα Δυαδικής Αναζήτησης για το στοιχείο $key=11$

Στη συνέχεια, θα εξετάσουμε αναλυτικά τη δυαδική αναζήτηση. Μία βασική υπόθεση που γίνεται στο σημείο αυτό είναι ότι η σύγκριση είναι τριών δρόμων ( $3$ -way comparison). Δηλαδή, με μοναδιαίο κόστος αποφασίζουμε να επιλέξουμε ένα δρόμο μεταξύ τριών.

Πρόταση 7.4.

Η πολυπλοκότητα της δυαδικής αναζήτησης είναι λογαριθμική.

Απόδειξη. Κάθε φορά που η σύγκριση του $k e y$ με το μεσαίο στοιχείο του πίνακα δεν καταλήγει σε ισότητα, η σύγκριση επαναλαμβάνεται σε υποπίνακα μισού μεγέθους σε σχέση με το μέγεθος του αρχικού. Επομένως, εύκολα προκύπτει η αναδρομική εξίσωση:

$\displaystyle T(0)$	$\displaystyle=$	$\displaystyle 0$
$\displaystyle T(n)$	$\displaystyle=$	$\displaystyle 1\hskip 130.882677pt{\rm αν\ \ }key=A[middle]$
	$\displaystyle=$	$\displaystyle 1+T(\lfloor(n+1)/2\rfloor-1)\hskip 28.452756pt{\rm αν\ \ }key<A[middle]$
	$\displaystyle=$	$\displaystyle 1+T(n-\lfloor(n+1)/2\rfloor)\hskip 28.452756pt{\rm αν\ \ }key>A[middle]$

Απλοποιούμε τη σχέση αυτή θεωρώντας τη χειρότερη περίπτωση (δηλαδή, αγνοούμε το δεύτερο σκέλος) και ότι $n=2^{k}-1$ για κάποιο ακέραιο αριθμό $k$ . Έτσι, προκύπτει:

T(2^{k}-1)\ =\ 1+T(2^{k-1}-1)

με αρχική συνθήκη $T(0)=0$ . Έτσι, διαδοχικά έχουμε:

$\displaystyle T(n)$	$\displaystyle=$	$\displaystyle 1+\left(1+T(2^{k-2}-1)\right)$
	$\displaystyle=$	$\displaystyle 1+\left(1+(1+T(2^{k-3}-1))\right)\ =\ \ldots$
	$\displaystyle=$	$\displaystyle i+T(2^{k-i}-1)$
	$\displaystyle=$	$\displaystyle k+T(0)\ =\ k\ =\ \log(n+1)$

Έτσι, λοιπόν, για $n=2^{k}-1$ προκύπτει ότι η πολυπλοκότητα της δυαδικής αναζήτησης είναι λογαριθμική. Εύκολα μπορεί να αποδειχθεί ότι η πολυπλοκότητα είναι $\Theta(\lceil\log(n+1)\rceil)$ .

Εναλλακτικά, μπορεί να διατυπωθεί η εξής πρόταση.

Πρόταση 7.5.

Η μέση τιμή του αριθμού των συγκρίσεων $E[T(n)]$ ή $E[T(n)]$ για μία επιτυχή ή μία ανεπιτυχή αναζήτηση δίνεται από τις σχέσεις:

	$\displaystyle{\rm E[T(n)]}$	$\displaystyle=$	$\displaystyle k-\frac{2^{k}-k-1}{n}$
	$\displaystyle{\rm E[A(n)]}$	$\displaystyle=$	$\displaystyle\lceil\log n\rceil$

όπου $k=\lfloor{\log}n\rfloor$ .

Απόδειξη. ‘Εστω ότι $n=2^{k}-1+m$ , όπου $m<2^{k}$ . Τότε ισχύει:

	$\displaystyle{\rm E[T(n)]}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\ \sum_{i=1}^{k-1}\ i\times 2^{i-1}+k\times m=$
		$\displaystyle=$	$\displaystyle\frac{2^{k-1}\times(k-2)+1+k\times m}{n}\ =\ k-\frac{2^{k}-k-1}{n}$

Η απόδειξη της περίπτωσης της ανεπιτυχούς αναζήτησης είναι προφανής.

7.3 Αναζήτηση Παρεμβολής

Η αναζήτηση παρεμβολής προσομοιάζει με τον τρόπο αναζήτησης σε ένα λεξικό ή σε έναν τηλεφωνικό κατάλογο. Κατά την αναζήτηση μίας λέξης, δεν ανοίγουμε το λεξικό αρχικά στη μέση και μετά στο $1/4$ ή στα $3/4$ , κοκ, δηλαδή δεν συνηθίζεται να κάνουμε δυαδική αναζήτηση. Για παράδειγμα, αν αναζητούμε μία λέξη που αρχίζει από Α, τότε ανοίγουμε το λεξικό προς την αρχή, αν αρχίζει από Ε πάλι ανοίγουμε προς την αρχή αλλά όχι τόσο κοντά στο Α, ενώ αν αρχίζει από Ω τότε ανοίγουμε προς το τέλος του λεξικού. Στη συνέχεια, αναλόγως αν η λέξη είναι λεξικογραφικά μεγαλύτερη ή μικρότερη, κινούμαστε προς το τέλος ή την αρχή του λεξικού παραλείποντας έναν αριθμό σελίδων, πριν λάβουμε την επόμενη απόφαση. Το πλήθος των παραλειπόμενων σελίδων είναι ανάλογο της αλφαβητικής απόστασης της σελίδας όπου βρισκόμαστε από τη ζητούμενη λέξη. Παραδείγματος χάριν, αν είμαστε στο Ε και η ζητούμενη λέξη αρχίζει από Η ή από Μ, τότε στην πρώτη περίπτωση θα μεταπηδήσουμε σε μικρότερη απόσταση σε σχέση με τη δεύτερη. Στην ουσία αυτή η τακτική, αρχικά, προσπαθεί να προσεγγίσει τη θέση όπου μπορεί να βρίσκεται το ζητούμενο στοιχείο και μετά να κινηθεί αναλόγως.

Έτσι, λοιπόν, στην αναζήτηση με παρεμβολή (interpolation search), όταν αναζητούμε το στοιχείο $x$ που βρίσκεται μεταξύ του $A[1]$ και του $A[n]$ ή γενικότερα μεταξύ του $A[left]$ και του $A[right]$ , τότε το στοιχείο που επιλέγεται για εξέταση είναι το στοιχείο που βρίσκεται στη θέση

\left\lfloor\frac{x-Α[left]}{Α[right]-Α[left]}\right\rfloor

(7.1)

Στην ουσία εξετάζοντας πόσο μεγαλύτερο είναι το ζητούμενο στοιχείο από το στοιχείο του αριστερού άκρου, καθώς και πόσο μεγαλύτερο είναι το στοιχείο του δεξιού από το στοιχείο του αριστερού άκρου, γίνεται εκτίμηση της θέσης του $x$ λαμβάνοντας το λόγο των δύο διαφορών. Ο επόμενος ψευδοκώδικας υλοποιεί τη μέθοδο.

Algorithm Interpolation(

k e y

)

low=1

;

high=n

2. while (

A[high]\geq key

) AND (

key>A[low]

) do

next=low+\left\lfloor\frac{key-A[low]}{A[high]-A[low]}(high-low)\right\rfloor

4. if

key>table[next]

then

low=next+1

5. else if

key<table[next]

then

high=next-1

6. else

low=next

7. if

key=A[low]

then return

l o w

else return

-1

;

Σχήμα 7.6: Απλός αλγόριθμος για αναζήτηση παρεμβολής.

Στο παράδειγμα του Σχήματος 7.7 παρατηρούμε ότι, όταν τα στοιχεία είναι ακέραιοι που διαφέρουν κατά μία μονάδα το ένα από το άλλο, τότε αυτή η εκτίμηση είναι ακριβής. Επίσης, αν τα στοιχεία διαφέρουν από τα γειτονικά τους κατά μία μικρή ποσότητα, και πάλι η εκτίμηση θα είναι σχετικά ακριβής. Όμως, όταν οι διαφορές μεταξύ των στοιχείων είναι σημαντικές, τότε οι εκτιμήσεις δεν θα είναι επαρκώς ακριβείς και θα χρειασθούν περισσότερες επαναλήψεις.

Ο χρόνος χειρότερης περίπτωσης για την αναζήτηση παρεμβολής είναι $Ο(n)$ , ενώ ο μέσος χρόνος είναι $Ο(\log{\log{n}})$ . Στη μέση περίπτωση η αναζήτηση παρεμβολής φαίνεται να υπερισχύει της δυαδικής αναζήτησης και αυτό είναι λογικό αφού τα προς εξέταση διαστήματα δεν υποδιπλασιάζονται σε κάθε βήμα αλλά μπορεί να γίνουν πολύ μικρότερα. Παρόλα αυτά, πειραματικά αποτελέσματα έδειξαν ότι η αναζήτηση παρεμβολής δεν εκτελεί πολύ λιγότερες συγκρίσεις, έτσι ώστε να αποφεύγεται το αυξημένο υπολογιστικό κόστος εύρεσης του $n e x t$ και να έχει καλύτερους χρόνους, εκτός και αν οι πίνακες είναι πολύ μεγάλοι. Για το λόγο αυτό, συχνά είναι προτιμότερο τα πρώτα βήματα να εκτελούν αναζήτηση παρεμβολής, έτσι ώστε το διάστημα να μειώνεται δραματικά και μετά να εκτελείται δυαδική αναζήτηση. Στη συνέχεια, θα μελετήσουμε αυτήν ακριβώς την παραλλαγή.

7.3.1 Δυαδική Αναζήτηση Παρεμβολής

Ακολουθεί ο ψευδοκώδικας της δυαδικής αναζήτησης παρεμβολής (binary interpolation search), ενώ στη συνέχεια θα σχολιασθεί και θα αναλυθεί η πολυπλοκότητα της μεθόδου.

Algorithm Interpolation_Binary(

k e y

)

left=1

;

right=n

;

size=right-left+1

next=\left\lfloor size\frac{key-A[left]}{A[right]-A[left]}\right\rfloor

3. while

(key\neq A[next])

i=0

;

size=right-left+1

5. if

(size\leq 3)

then do sequential search

6. if

(key\geq A[next])

7. while

(key>A[next+i\sqrt{size}-1])

i=i+1

right=next+i\sqrt{size}

10.

left=next+(i-1)\sqrt{size}

11. else if

(key<A[next])

12. while

(key<A[next-i\sqrt{size}+1])

13.

i=i+1

14.

right=next-(i-1)\sqrt{size}

15.

left=next-i*\sqrt{size}

16.

next=left+\left\lfloor(right-left+1)\frac{key-A[left]}{A[right]-A[left]}\right% \rfloor-1

17. if

(key==A[next])

then return

n e x t

18. else return

-1

Σχήμα 7.8: Aλγόριθμος αναζήτησης δυαδικής παρεμβολής.

Σχετικά με τον ανωτέρω κώδικα, που είναι ενδεικτικός περισσότερο και σε καμία περίπτωση δεσμευτικός, παρατηρούμε τα εξής:

•

Στην ουσία μετά το βήμα παρεμβολής (γραμμές $2$ και $16$ , έκφραση 7.1) αναζητούμε γραμμικά με άλματα μεγέθους $\sqrt{size}$ , για να προσδιορισθεί το υποδιάστημα που περιέχει το $k e y$ . Στη συνέχεια, επαναλαμβάνεται η ίδια διαδικασία για το νέο διάστημα, όπως φαίνεται στο Σχήμα 7.9.

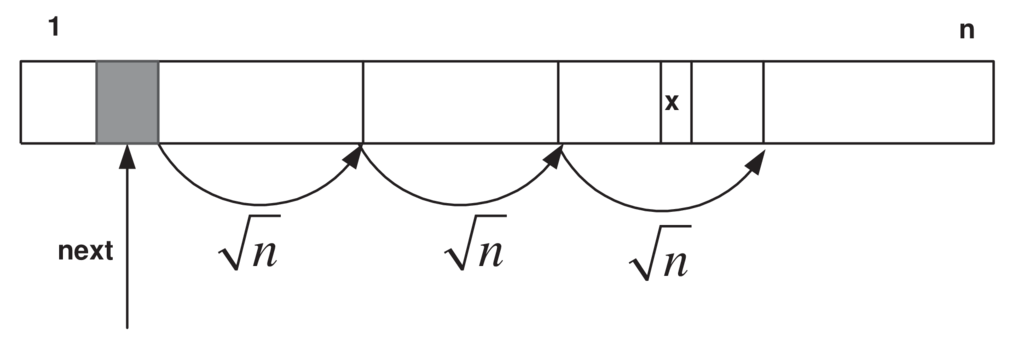
Σχήμα 7.9: Αναζήτηση δυαδικής παρεμβολής.
•

Για να γίνει απλούστερος ο ψευδοκώδικας, στη γραμμή $5$ θεωρούμε ότι για σχετικά μικρά μεγέθη εκτελούμε γραμμική αναζήτηση, χωρίς αυτό να επηρεάζει την ασυμπτωτική συμπεριφορά του αλγορίθμου. Για παράδειγμα, κάλλιστα θα μπορούσε να εκτελεσθεί γραμμική αναζήτηση και για $s i z e$ μικρότερο του 5.
•

Ο ανωτέρω ψευδοκώδικας δεν χειρίζεται κάποιες ακραίες περιπτώσεις, όπως όταν το αναζητούμενο στοιχείο $k e y$ είναι μεγαλύτερο από κάθε στοιχείο του πίνακα $A$ ή αν ενδεχομένως το βήμα μήκους $\sqrt{size}$ υπερβεί το δεξιό άκρο του υποπίνακα. Η διαχείριση των προβλημάτων αυτών είναι απλή και αφήνεται ως άσκηση στον αναγνώστη.

Πρόταση 7.6.

Ο μέσος χρόνος της δυαδικής αναζήτησης παρεμβολής είναι $O(\log{\log{n}})$ .

Απόδειξη. Έστω ότι όλα τα στοιχεία του πίνακα $A$ επιλέγονται ισοπίθανα από το διάστημα $[0,1]$ . Επίσης, έστω ότι $C$ είναι το πλήθος των συγκρίσεων μέχρι να βρεθεί το κατάλληλο υποδιάστημα μεγέθους $\sqrt{n}$ που περιέχει το κλειδί $k e y$ που ψάχνουμε. Έστω ότι το κλειδί $k e y$ θα βρίσκεται στη θέση $pos(key)$ . Αν το $k e y$ δεν είναι μέσα στον πίνακα, τότε το $pos(key)$ είναι το μεγαλύτερο στοιχείο στο πίνακα που είναι μικρότερο από το $k e y$ . Τέλος, έστω $P_{i}$ η πιθανότητα, ότι θα χρειασθούν τουλάχιστον $i$ συγκρίσεις για να προσδιορισθεί το επίμαχο υποδιάστημα. Είναι βέβαιο ότι θα χρειασθούν $2$ συγκρίσεις τουλάχιστον και, επομένως, ισχύει: $P_{1}=P_{2}=1$ . Τότε ο αριθμός συγκρίσεων θα είναι:

C=\sum_{i\geq 3}{i(P_{i}-P_{i+1})}+2=\sum_{i\geq 1}{P_{i}}+2

Για το $P_{i}$ ισχύει:

P_{i}\leq\Pr\left[|pos(key)–-next|\geq(i-2)\sqrt{n}\right],\ i\geq 3

Θα χρησιμοποιήσουμε την ανισότητα του Chebyschev, για να φράξουμε από πάνω την πιθανότητα $P_{i}$ :

\Pr\left[|X-\mu|\geq\epsilon\right]\leq\frac{\sigma^{2}}{\epsilon^{2}}

για τυχαία μεταβλητή $X$ με μέση τιμή $\mu$ και διασπορά $\sigma^{2}$ και για κάποια ποσότητα $\epsilon$ .

Έστω, λοιπόν, $X$ η τυχαία μεταβλητή, που λαμβάνει τιμές το πλήθος των $A_{i}\leq key$ , όπου $A_{i},\ 1\leq i\leq n$ είναι τα στοιχεία του πίνακα $A$ . Η πιθανότητα $p$ , ώστε ένα $A_{i}$ να είναι μικρότερο του $k e y$ , είναι:

p=\frac{key-A_{0}}{A_{n+1}-A_{0}}

όπου $Α_{0}$ είναι το κάτω όριο του διαστήματος που ψάχνουμε (στην αρχική κλήση της αναζήτησης παρεμβολής $A_{0}=0$ ) και $A_{n+1}$ είναι το πάνω όριο του διαστήματος που ψάχνουμε (ομοίως αρχικά είναι $A_{n+1}=1$ ). Η πιθανότητα $\Pr[X=j]$ είναι στην πραγματικότητα η πιθανότητα η θέση του $k e y$ να ισούται με $j$ . Δεδομένου ότι τα $A_{1},A_{2},...,A_{n}$ επιλέγονται ισοπίθανα αυτή η πιθανότητα θα ακολουθεί τη διωνυμική κατανομή:

\Pr[X=j]={n\choose j}p^{j}(1-p)^{n-j}

Η $X$ ακολουθεί τη δυωνυμική κατανομή με μέση τιμή $\mu=pn$ και διασπορά $\sigma^{2}=p(1-p)n\leq\frac{n}{4}$ (αφού για $p=\frac{1}{2}$ η συνάρτηση $f(p)=p(1-p)$ μεγιστοποιείται όταν $p\in[0,1]$ ). Παρατηρούμε ότι $\mu=next$ , δηλαδή ότι ο δείκτης παρεμβολής είναι ίσος με τη μέση τιμή της $X$ . Άρα, χρησιμοποιώντας την ανισότητα Chebyschev:

	$\displaystyle P_{i}$	$\displaystyle\leq$	$\displaystyle\Pr\left[\ \|pos(key)–-next\|\geq(i-2)\sqrt{n}\ \right]$
		$\displaystyle\leq$	$\displaystyle\frac{p(1-p)n}{((i-2)\sqrt{n})^{2}}=\frac{p(1-p)}{(i-2)^{2}}\leq% \frac{1}{4(i-2)^{2}}$

Συνεπώς, ισχύει:

C\leq 2+\sum_{i\geq 3}\frac{1}{4(i-2)^{2}}=2+\frac{1}{4}\sum_{k\geq 1}\frac{1}% {k^{2}}=2+\frac{1}{4}\frac{\pi^{2}}{6}\approx 2.4

Αν $Τ(n)$ είναι το μέσο πλήθος των συγκρίσεων, τότε:

Τ(n)\leq C+Τ(\sqrt{n})

για $n\geq 3$ και $Τ(1)\leq 1,Τ(2)\leq 2$ . Η αναδρομική αυτή περιγράφει τη διαδικασία εύρεσης με παρεμβολή, αφού έπειτα από $2.4$ κατά μέσο όρο συγκρίσεις το υποπρόβλημα που λύνεται στην 1η (και άρα στις επόμενες) αναδρομική κλήση έχει μέγεθος $\sqrt{n}$ . Λύνοντας τη συγκεκριμένη αναδρομική διαδικασία προκύπτει:

Τ(n)\leq 2+2.4\log{\log{n}}

Πρόταση 7.7.

Στην χειρότερη περίπτωση ο χρόνος της δυαδικής αναζήτησης παρεμβολής είναι $O(\sqrt{n})$ .

Απόδειξη. Στην πρώτη εκτέλεση του βρόγχου while της εντολής $12$ εκτελούνται το πολύ $\sqrt{n}$ συγκρίσεις, στη δεύτερη το πολύ $\sqrt{\sqrt{n}}$ , στην τρίτη $\sqrt{\sqrt{\sqrt{n}}}$ κοκ. Δηλαδή ισχύει:

n^{\frac{1}{2}}+n^{\frac{1}{4}}+n^{\frac{1}{8}}+\ldots=O(\sqrt{n})

Ο χρόνος χειρότερης περίπτωσης μπορεί να βελτιωθεί από O( $\sqrt{n}$ ) σε O( $\log{n}$ ) χωρίς να χειροτερεύει ο χρόνος μέσης περίπτωσης. Αντί το $i$ να αυξάνεται γραμμικά (δηλαδή, με την εντολή $13$ : $i=i+1$ μέσα στο βρόγχο while), αυτό να αυξάνεται εκθετικά (δηλαδή, με μία εντολή: $i=2*i$ ). Έτσι, τα άλματα γίνονται συνεχώς μεγαλύτερα κρατώντας το αριστερό άκρο σταθερό (όπως στο Σχήμα 7.10), με αποτέλεσμα το τελευταίο υποδιάστημα να είναι πολύ μεγαλύτερο από $\sqrt{n}$ . Μόλις βρεθεί αυτό το υποδιάστημα εφαρμόζουμε δυαδική αναζήτηση στα στοιχεία μέσα σε αυτό που απέχουν κατά $\sqrt{n}$ και έτσι προκύπτει το ζητούμενο υποδιάστημα μεγέθους $\sqrt{n}$ . Πιο συγκεκριμένα:

1.

Με μεγάλα εκθετικά βήματα εξέτασε τα διαστήματα: $[next,next+2^{0}\sqrt{n}]$ , $[next,next+2^{1}\sqrt{n}],[next,next+2^{2}\sqrt{n}],[next,next+2^{3}\sqrt{n}],\ldots$ , $[next,next+2^{i}\sqrt{n}]$ μέχρι να βρεθεί $j$ τέτοιο ώστε:

$A[next+2^{j-1}\sqrt{n}]<key\leq A[next+2^{j}\sqrt{n}]$
2.

Αναζήτησε δυαδικά στα στοιχεία των θέσεων: $next+2^{j-1}\sqrt{n},next+[2^{j-1}+1]\sqrt{n},next+[2^{j-1}+2]\sqrt{n},\ldots,% next+2^{j}\sqrt{n}$ . Δηλαδή, ψάξε δυαδικά στα στοιχεία που απέχουν απόσταση $\sqrt{n}$ στο διάστημα που βρέθηκε από το Βήμα 1. Έτσι, προκύπτει τελικά ένα διάστημα μεγέθους $\sqrt{n}$ .

Σχήμα 7.10: Βελτίωση με αναζήτηση άλματος.

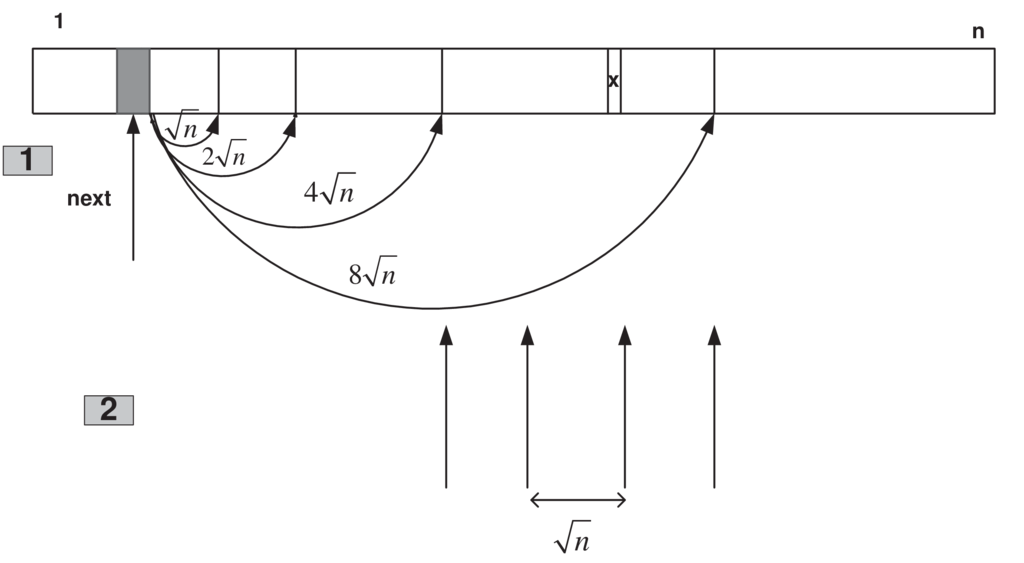
Έστω ότι για το πρώτο βήμα εκτελούμε στη χειρότερη περίπτωση $i$ συγκρίσεις. Αυτό σημαίνει ότι:

2^{i}\sqrt{n}=n\Rightarrow i=\log{\sqrt{n}}

Συνεπώς, για το πρώτο βήμα χρειάζεται χρόνο $Ο(\log{\sqrt{n}})$ , ενώ για το δεύτερο βήμα χρειάζεται χρόνος $\log 2^{i-1}=O(i-1)=Ο(\log{\sqrt{n}})$ . Έτσι, προκύπτει ότι κάθε επανάληψη του while θα χρειάζεται $O(\log{i})$ χρόνο στη χειρότερη περίπτωση. Άρα, συνολικά θα χρειασθεί χρόνος:

$\displaystyle\log{\sqrt{n}}+\log{\sqrt{\sqrt{n}}}+\log{\sqrt{\sqrt{\sqrt{n}}}}+\ldots$	$\displaystyle=$	$\displaystyle\log n^{\frac{1}{2}}+\log n^{\frac{1}{4}}+\log n^{\frac{1}{8}}+\ldots$
	$\displaystyle=$	$\displaystyle\frac{1}{2}\log{n}+{\frac{1}{4}}\log{n}+{\frac{1}{8}}\log{n}+\ldots$
	$\displaystyle=$	$\displaystyle(\frac{1}{2}+{\frac{1}{4}}+{\frac{1}{8}}+\ldots)\log{n}$
	$\displaystyle=$	$\displaystyle O(\log{n})$

Ο χρόνος μέσης περίπτωσης δεν αλλάζει, υπό την προϋπόθεση ότι όλα τα στοιχεία του πίνακα $A$ επιλέχθηκαν ισοπίθανα από το διάστημα $[0,1]$ . Αυτό συμβαίνει διότι σε κάθε επανάληψη της αναδρομικής σχέσης το κόστος είναι $Ο(\log{i}),i\leq\log{n})$ , συνεπώς συνολικά το αναμενόμενο κόστος θα είναι $Ο(\log{\log{n}})$ . Η περίπτωση τα στοιχεία του πίνακα $A$ να μην επιλέχθηκαν ισοπίθανα από το διάστημα $[0,1]$ εξετάζεται στη συνέχεια.

7.3.2 Γενίκευση της Μεθόδου Παρεμβολής

Κάθε μέθοδος αναζήτησης (δυαδική ή παρεμβολής) προσπαθεί να εντοπίσει το προς αναζήτηση στοιχείο περιορίζοντας σε κάθε επανάληψη το σχετικό διάστημα. Ο περιορισμός αυτός γίνεται με επιλογή ενός στοιχείου στο τρέχον διάστημα και με βάση αυτό το στοιχείο γίνεται ο διαχωρισμός του διαστήματος σε δύο υποδιαστήματα. Στη δυαδική αναζήτηση γίνεται διχοτόμηση επιλέγοντας το μεσαίο στοιχείο του διαστήματος σύμφωνα με τον τύπο:

next_{BIN}\leftarrow\left\lfloor\frac{left+right}{2}\right\rfloor

ενώ στην αναζήτηση παρεμβολής επιλέγοντας το στοιχείο σύμφωνα με τον τύπο:

next_{ΙΝΤ}\leftarrow\left\lfloor\frac{key-A[left]}{A[right]-A[left]}(right-% left)\right\rfloor+left

Στη βιβλιογραφία έχουν προταθεί συνθετότεροι αλλά και αποτελεσματικότεροι τρόποι, με συνεχείς εναλλαγές στον τρόπο επιλογής του στοιχείου $n e x t$ .

Μέθοδος Alternate.

Το στοιχείο διαχωρισμού υπολογίζεται στη μία επανάληψη με βάση τη δυαδική αναζήτηση, ενώ στην επόμενη με βάση την αναζήτηση παρεμβολής κοκ. Δηλαδή:

–

Αν $i\equiv 1\;\;(\mathop{{\rm mod}}2)$ , τότε $next\leftarrow next_{INT}$ , ενώ
–

Αν $i\equiv 0\;\;(\mathop{{\rm mod}}2)$ , τότε $next\leftarrow next_{BIN}$

Μέθοδος Retrieve.

Σε κάθε $i$ -οστή επανάληψη της μεθόδου το στοιχείο διαχωρισμού επιλέγεται ως εξής:

–

Αν $i\equiv 1\;\;(\mathop{{\rm mod}}3)$ , τότε $next\leftarrow min\{next^{+},right-1\}$
–

Αν $i\equiv 2\;\;(\mathop{{\rm mod}}3)$ , τότε $next\leftarrow min\{next^{-},left+1\}$
–

Αν $i\equiv 0\;\;(\mathop{{\rm mod}}3)$ , τότε $next\leftarrow next_{BIN}$

όπου

next^{+}\leftarrow\left\lceil next_{INT}+\Delta\right\rceil

next^{-}\leftarrow\left\lceil next_{INT}-\Delta\right\rceil

\Delta\leftarrow\theta(right-left)(Α[right]-Α[left])^{\alpha}+\phi\sqrt{right-left}

ενώ τα $0<\alpha\leq 1$ και $\phi,\theta>0$ είναι παράμετροι της μεθόδου.

Πρόταση 7.8.

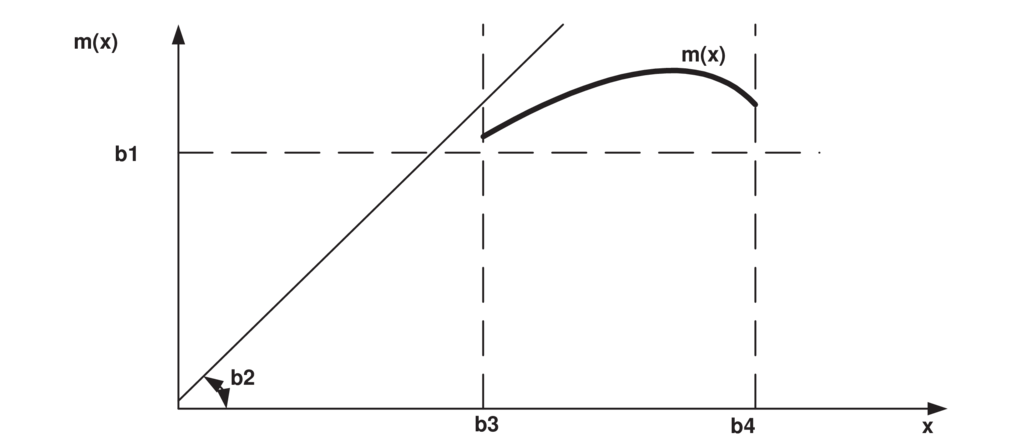
Όταν τα στοιχεία του πίνακα $Α$ επιλέγονται από το διάστημα $[0,1]$ με ομαλή κατανομή, τότε ο μέσος χρόνος για την Alternate είναι $Ο(\sqrt{\log{n}})$ , ενώ για την Retrieve είναι $Ο(\log{\log{n}})$ .

Ορισμός 7.1.

Μία κατανομή $m(x)$ καλείται ομαλή, αν υπάρχουν $b_{1},b_{2},b_{3},b_{4}$ για τα οποία ισχύει:

1.

$m(x)\geq b_{1}>0$ όταν $b_{3}<x<b_{4}$
2.

$|m^{\prime}(x)|\leq b_{2}$
3.

$m(x)=0$ όταν $x\leq b_{3}\mbox{ και }x\geq b_{4}$

όπως παρουσιάζεται στο παράδειγμα του Σχήματος 7.11.

7.4 Κατακερματισμός

Με τον όρο κατακερματισμός (hashing) δηλώνεται ένα πολύ ευρύ αντικείμενο, τόσο σε θεωρητικό επίπεδο όσο και σε πρακτικό. Το πρόβλημα του σχεδιασμού αποτελεσματικών τεχνικών κατακερματισμού προκύπτει λόγω των πολλών διαφορετικών περιβαλλόντων και εφαρμογών όπου μπορεί να εφαρμοσθεί, όπως σε περιπτώσεις μεταγλωττιστών, βάσεων δεδομένων, ανάκτησης πληροφοριών κλπ. Υπό προϋποθέσεις οι μέθοδοι του κατακερματισμού έχουν πολύ καλή και σταθερή επίδοση, που υπερτερεί της δυαδικής αναζήτησης που εξετάσαμε προηγουμένως.

Εναλλακτική ονομασία του κατακερματισμού είναι μετασχηματισμός κλειδιού σε διεύθυνση (key to address transfrmation). Ο μετασχηματισμός αυτός επιτυγχάνεται με τη βοήθεια της συνάρτησης κατακερματισμού (hashing function), η οποία όμως δεν είναι αμφιμονοσήμαντη. Δηλαδή, είναι δυνατόν δύο διαφορετικά κλειδιά να αντιστοιχίζονται στην ίδια διεύθυνση του πίνακα. Το φαινόμενο αυτό ονομάζεται σύγκρουση (collision) και αποτελεί το μειονέκτημα της μεθόδου. Ουσιαστικά, κάθε μέθοδος κατακερματισμού προτείνει και μία διαφορετική τεχνική επίλυσης των συγκρούσεων. Το ερώτημα που τίθεται είναι πόσο συχνά μπορεί να εμφανισθεί περίπτωση σύγκρουσης. Στο ερώτημα αυτό απαντά το επόμενο παράδειγμα του παραδόξου των γενεθλίων (birthday paradox).

Το παράδοξο των γενεθλίων

Έστω ότι επιλέγονται τυχαία άτομα από το πλήθος. Κάθε φορά ελέγχουμε αν το επιλεγόμενο άτομο έχει γενέθλια την ίδια ημέρα με τους ήδη επιλεγέντες. Η ερώτηση είναι πόσα άτομα πρέπει να επιλεγούν, ώστε η πιθανότητα δύο ή περισσότερα άτομα να έχουν την ίδια ημέρα γενέθλια να είναι περισσότερο από 50%. Κατ’αρχάς υποθέτουμε ότι όλες οι ημέρες του χρόνου είναι ισοπίθανο να είναι ημέρες γενεθλίων. Σε μία τέτοια περίπτωση, η πιθανότητα δύο άτομα να έχουν την ίδια ημέρα γενέθλια είναι $\frac{1}{365}$ , οπότε η πιθανότητα δύο άτομα να μην έχουν την ίδια ημέρα γενέθλια είναι $1-\frac{1}{365}$ . Ομοίως, η πιθανότητα το τρίτο επιλεγόμενο άτομο να μην έχει γενέθλια με τους δύο προηγούμενους επιλεγέντες είναι $1-\frac{2}{365}$ . Με τη λογική αυτή καταλήγουμε ότι πρέπει να προσδιορίσουμε το $i$ εκείνο για το οποίο ισχύει η σχέση:

\left(1-\frac{1}{365}\right)\ \left(1-\frac{2}{365}\right)\ \ldots\ \left(1-% \frac{i}{365}\right)\ \leq\ 1/2

(7.2)

Αξιοποιώντας τη σχέση $1+x\leq e^{x}$ (που ισχύει για κάθε $x$ όπως είδαμε στο Κεφάλαιο 2), προκύπτει η ισοδύναμη σχέση:

e^{-1/365}\ e^{-2/365}\ \ldots\ e^{-i/365}\ \leq\ e^{\ln{1/2}}\ \ \Rightarrow

(7.3)

e^{-1/365\sum_{j=1}^{i}j}\ \leq\ e^{\ln{1/2}}\ \ \Rightarrow

(7.4)

-\frac{1}{365}\sum_{j=1}^{i}j\ \leq\ \ln\frac{1}{2}=-\ln 2\ \ \Rightarrow

(7.5)

\frac{1}{365}\ \frac{i(i+1)}{2}\ \geq\ \ln 2

(7.6)

Με κατάλληλη άλγεβρα και λύνοντας την παραγόμενη τετραγωνική εξίσωση φθάνουμε στο συμπέρασμα ότι η ζητούμενη τιμή είναι $i=23$ . Το αποτέλεσμα αυτό θεωρείται παράδοξο, καθώς κάποιος θα ανέμενε ότι η συγκεκριμένη πιθανότητα (δηλαδή, δύο ή περισσότερα άτομα να έχουν την ίδια ημέρα γενέθλια να είναι περισσότερο από 50%) θα συνέβαινε για ένα μεγαλύτερο σύνολο ατόμων. Από το παράδοξο αυτό μπορούμε να σκεφτούμε την αναλογία σε σχέση με τον κατακερματισμό, δηλαδή ότι οι 365 ημέρες αντιστοιχούν σε θέσεις ενός πίνακα, ενώ τα άτομα αντιστοιχούν σε κλειδιά που εισάγονται στον πίνακα. Με βάση τη δυωνυμική κατανομή προκύπτει ότι η πιθανότητα κατά την εισαγωγή $n$ κλειδιών, $k$ από αυτά να συμπέσουν στην ίδια θέση είναι:

{n\choose k}\ \left(\frac{1}{n}\right)^{k}\ \left(1-\frac{1}{n}\right)^{n-k}

(7.7)

Για $n$ αρκετά μεγάλο η προηγούμενη σχέση προσεγγίζεται από 1/ $(ek!)$ . Από την προηγούμενη δυωνυμική κατανομή συνάγεται ότι αν σε πίνακα 1000 θέσεων εισαχθούν $n=1000$ κλειδιά, τότε η πιθανότητα σε μία θέση του πίνακα να αντιστοιχηθούν $k$ κλειδιά δίνεται από τον Πίνακα 7.1. Συνεπώς, η πιθανότητα να παρουσιασθούν συγκρούσεις είναι σημαντικότατη και για το λόγο αυτό έχουν προταθεί τόσες πολλές τεχνικές αντιμετώπισης του προβλήματος.

$k$	πιθανότητα $k$
	συγκρούσεων
0	37%
1	37%
2	18%
3	6%
4	1.5 %
5	0.3%

Table 7.1: Πιθανότητα σύγκρουσης σε πίνακα 1000 θέσεων για 1000 κλειδιά.

7.4.1 Γραμμικός Κατακερματισμός

Ο κλειστός κατακερματισμός (closed hashing) είναι μία οικογένεια αλγορίθμων που δεν χρησιμοποιούν δείκτες για το χειρισμό των πινάκων. Στην οικογένεια αυτή ανήκουν αρκετές τεχνικές, μεταξύ των οποίων η γραμμική αναζήτηση (linear probing), η τετραγωνική αναζήτηση (quadratic probing), και o διπλός κατακερματισμός (double hashing). Την απλούστερη τεχνική της γραμμικής αναζήτησης θα εξετάσουμε στη συνέχεια, ενώ στο Κεφάλαιο LABEL:section_quadratic θα εξετάσουμε την τετραγωνική αναζήτηση.

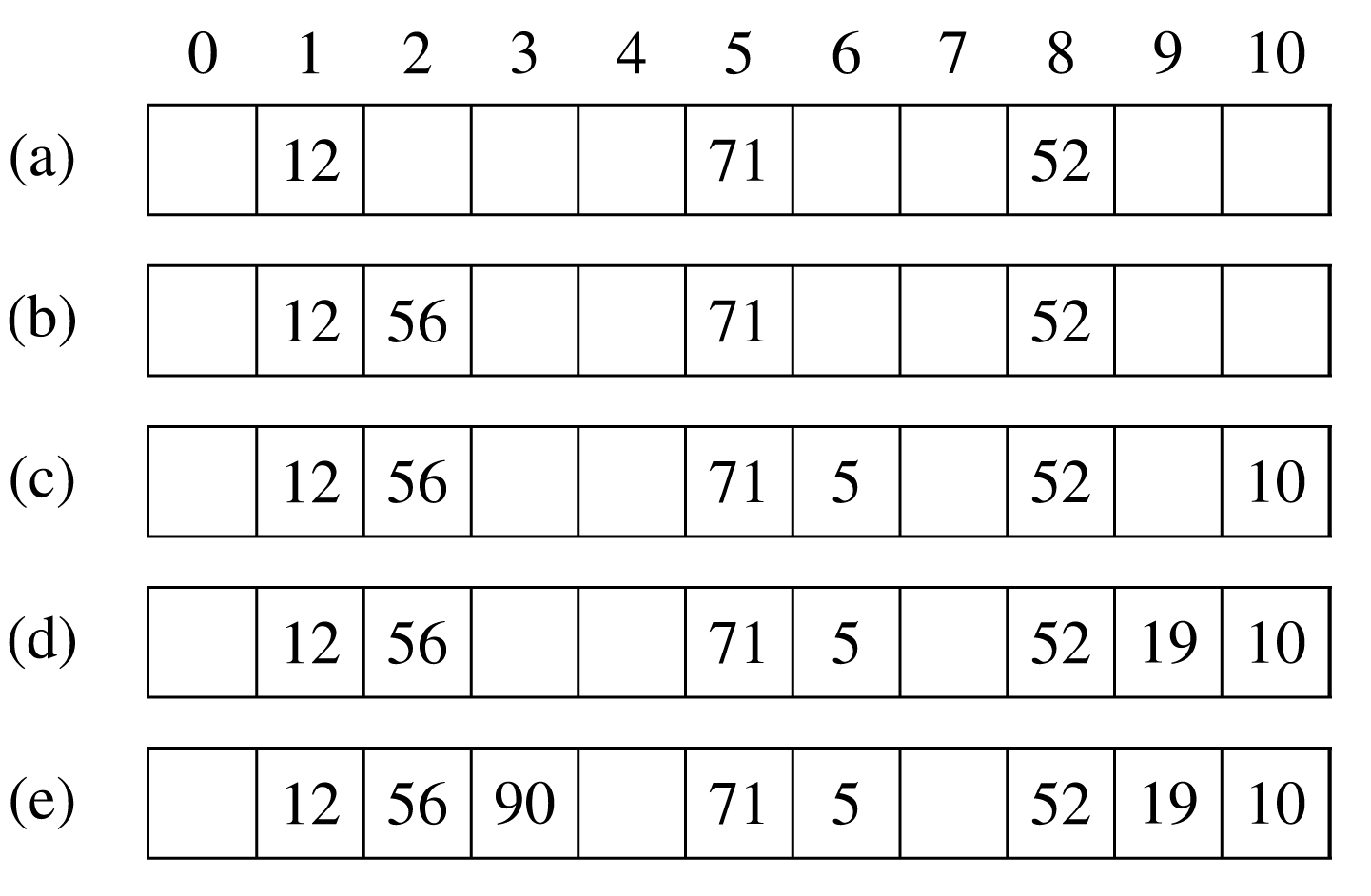
Η επόμενη διαδικασία insert παριστά τον αλγόριθμο εισαγωγής υποθέτοντας ότι ο πίνακας A έχει m θέσεις. Σύμφωνα με τη μέθοδο αυτή, κατά την εισαγωγή ενός κλειδιού καλείται η συνάρτηση κατακερματισμού που δίνει τη διεύθυνση του πίνακα όπου θα πρέπει να εισαχθεί το κλειδί. Αν η θέση δεν είναι κατειλημμένη, τότε το κλειδί εισάγεται και η διαδικασία τερματίζει. Αν η θέση είναι κατειλημμένη, τότε δοκιμάζεται η επόμενη θέση διαδοχικά μέχρι να τοποθετηθεί το κλειδί ή να γίνουν m προσπάθειες, γεγονός που δηλώνει ότι ο πίνακας είναι πλήρης.

Algorithm Insert(

k e y

)

address=hash(key)

;

count=0

2. while

(A[address]\neq 0)

AND

(count\leq m)

count=count+1

address=(address+1)\mod{m}

5. if

A[address]==0

then

A[address]=key

; return TRUE

7. else return FALSE

Σχήμα 7.12: Η διαδικασία ένθεσης στον γραμμικό κατακερματισμό.

Το επόμενο σχήμα δείχνει ένα παράδειγμα της δομής αυτής με $m=11$ και $n=8$ . Πιο συγκεκριμένα, εισάγονται με τη σειρά τα κλειδιά 52, 12, 71, 56, 5, 10, 19 και 90, ενώ η χρησιμοποιούμενη συνάρτηση κατακερματισμού είναι: hash(key) = key mod m.

Σχήμα 7.13: Κατακερματισμός με γραμμική αναζήτηση.

Παρόμοιο είναι και το σκεπτικό του αλγορίθμου αναζήτησης, όπως φαίνεται στην επόμενη διαδικασία search, που επιστρέφει τη διεύθυνση του πίνακα όπου το κλειδί είναι αποθηκευμένο ή επιστρέφει την τιμή $-1$ , αν το κλειδί δεν υπάρχει στον πίνακα.

Algorithm Search(

k e y

)

address=hash(key)

;

count=0

2. while

(A[address]\neq key)

AND

(count\leq m)

count=count+1

address=(address+1)\mod{m}

5. if

count==m

then return

-1

else return

a d d r e s s

Σχήμα 7.14: Η διαδικασία εύρεσης ενός στοιχείου

k e y

στον γραμμικό κατακερματισμό.

Θα αναλύσουμε την επίδοση της μεθόδου για την περίπτωση της επιτυχούς και της ανεπιτυχούς αναζήτησης, Ε και Α αντίστοιχα, δηλαδή όταν αναζητούμε ένα υπαρκτό ή ανύπαρκτο κλειδί μέσα στον πίνακα. Υποθέτουμε ότι η συνάρτηση κατακερματισμού παράγει μία τυχαία διάταξη των κλειδιών, οπότε οι θέσεις στον πίνακα εξετάζονται με τυχαίο τρόπο. Αρχικά, θα ασχοληθούμε με την ανεπιτυχή αναζήτηση. Οι παράμετροι που υπεισέρχονται στην ανάλυση της επίδοσης της μεθόδου είναι το μέγεθος $m$ του πίνακα, το πλήθος των κλειδιών $n\leq m$ και ο παράγοντας φόρτωσης (load factor) $\alpha=n/m\leq 1$ .

Πρόταση 7.9.

Η μέση τιμή του αριθμού των συγκρίσεων κατά τη γραμμική αναζήτηση, σε περίπτωση επιτυχούς και ανεπιτυχούς αναζήτησης είναι αντιστοίχως:

{\rm E}\ \approx\ \frac{1}{\alpha}\ \ln{\frac{1}{1-\alpha}}

και

{\rm A}\ \approx\ \frac{1}{1-\alpha}

Απόδειξη. Ας υποθέσουμε ότι μία ανεπιτυχής αναζήτηση απαιτεί $i$ προσπελάσεις ( $1\leq i\leq m$ ) στον πίνακα. Στην περίπτωση αυτή θα γίνουν $i-1$ προσπελάσεις σε κατειλημμένες θέσεις του πίνακα, ενώ η $i$ -οστή θα προσπελάσει μία κενή θέση. Επομένως, αν εξαιρέσουμε αυτήν την ομάδα των $i$ συνεχόμενων θέσεων, μένουν $m-i$ θέσεις εκ των οποίων κατειλημμένες είναι οι $n-i+1$ θέσεις. Το πλήθος των τρόπων που μπορεί να εμφανισθεί αυτή η περίπτωση είναι $m-i\choose n-i+1$ , ενώ το σύνολο των περιπτώσεων είναι $m\choose n$ . Συνεπώς, η πιθανότητα να απαιτηθούν $i$ προσπελάσεις είναι:

P_{i}\ =\ \frac{{m-i\choose n-i+1}}{{m\choose n}}

(7.8)

Άρα ισχύει:

{\rm A}\ =\ \sum_{i=1}^{m}\ i\ P_{i}\ =\ (m+1)-\sum_{i=1}^{m}\ (m+1-i)\ P_{i}

(7.9)

Για το τελευταίο άθροισμα ισχύει:

(m+1-i)\ P_{i}\ =\ (m-i+1)\ \frac{{m-i\choose n-i+1}}{{m\choose n}}\ =\ \ldots% \ =\ \frac{m-n}{{m\choose n}}\ {m-i+1\choose m-n}

(7.10)

Επομένως, επιστρέφοντας στο A έχουμε:

{\rm A}\ =\ (m+1)-\frac{m-n}{{m\choose n}}\ \sum_{i=1}^{m}\ {{m-i+1\choose m-n}}

(7.11)

Με βάση την ταυτότητα των συνδυασμών, την οποία γνωρίζουμε από το Κεφάλαιο 2, έχουμε διαδοχικά:

{\rm A}\ =\ (m+1)-(m-n)\ \frac{{m+1\choose n}}{{m\choose n}}\ =\ \ldots\ =\ % \frac{m+1}{m-n+1}\ \approx\ \frac{1}{1-\alpha}

(7.12)

Το αποτέλεσμα αυτό εξηγείται και διαισθητικά. Το $\alpha$ δηλώνει το ποσοστό των κατειλημμένων θέσεων, οπότε το $1-\alpha$ δηλώνει το ποσοστό των κενών θέσεων. Άρα, αναμένουμε να εκτελέσουμε $\frac{1}{1-\alpha}$ προσπελάσεις, πριν να εντοπίσουμε μία κενή θέση.

Για να φθάσουμε στην αντίστοιχη έκφραση για την επιτυχή αναζήτηση αρκεί να παρατηρήσουμε ότι το πλήθος των προσπελάσεων για την εύρεση ενός κλειδιού ισούται με το πλήθος των προσπελάσεων που είναι απαραίτητες για την εισαγωγή του (δηλαδή, $i-1$ προσπελάσεις σε κατειλημμένες θέσεις και μία προσπέλαση σε κενή θέση). Συνεπώς, καταλήγουμε ότι:

$\displaystyle{\rm E}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\ \sum_{i=0}^{n-1}{\rm A}\ =\ \frac{1}{n}\ \sum_{i=0}^% {n-1}\ \frac{m+1}{m-i+1}$
	$\displaystyle=$	$\displaystyle\frac{m+1}{n}\ (H_{m+1}-H_{m-n+1})\ \approx\ \frac{m+1}{n}\ \left% (\ln(m+1)-\ln(m-n+1)\right)$
	$\displaystyle=$	$\displaystyle\frac{m+1}{n}\ \ln\frac{m+1}{m-n+1}\ \approx\ \frac{1}{\alpha}\ln% \frac{1}{1-\alpha}$

Στις ίδιες εκφράσεις για τα E και A μπορούμε να καταλήξουμε στηριζόμενοι σε ένα διαφορετικό σκεπτικό. Έστω ότι με $P_{i}$ συμβολίζουμε την πιθανότητα να απαιτηθούν ακριβώς $i$ προσπελάσεις για μία ανεπιτυχή αναζήτηση, οπότε ισχύει:

{\rm A}\ =\ 1+\sum_{i=0}^{\infty}i\ P_{i}

(7.13)

Έστω επίσης ότι με $Q_{i}$ συμβολίζουμε την πιθανότητα να απαιτηθούν τουλάχιστον $i$ προσπελάσεις, οπότε ισχύει η σχέση:

\sum_{i=0}^{\infty}i\ P_{i}\ =\ \sum_{i=1}^{\infty}Q_{i}

(7.14)

Το πρόβλημα, λοιπόν, ανάγεται στον προσδιορισμό του $Q_{i}$ . Προφανώς, ισχύει $Q_{1}=\alpha$ , $Q_{2}=Q_{1}\frac{n-1}{m-1}$ , ενώ γενικώς ισχύει:

Q_{i}\ =\ \frac{n}{m}\ \frac{n-1}{m-1}\ \ldots\ \frac{n-i+1}{m-i+1}\ \leq\ % \left(\frac{n}{m}\right)^{i}\ =\ \alpha^{i}

(7.15)

Επανερχόμενοι στη σχέση για το E $(n)$ έχουμε:

{\rm A}\ =\ \sum_{i=1}^{\infty}Q_{i}\ \leq\ 1+\alpha+\alpha^{2}+\alpha^{3}+% \ldots\ =\ \frac{1}{1-\alpha}

(7.16)

7.4.2 Τετραγωνική Αναζήτηση

Η επίδοση της γραμμικής αναζήτησης δεν είναι ιδιαίτερα ελκυστική και οφείλεται στο φαινόμενο της πρωτεύουσας συγκέντρωσης (primary clustering), δηλαδή της σύγκρουσης σε διάφορες περιοχές του πίνακα κλειδιών που προέρχονται από διαφορετικές αρχικές διευθύνσεις, δηλαδή δεν είναι συνώνυμα. Για τη μείωση της πρωτεύουσας συγκέντρωσης συχνά χρησιμοποιούνται μη γραμμικές μέθοδοι αναζήτησης της επόμενης διαθέσιμης θέσης. Μία τέτοια μέθοδος είναι η τετραγωνική αναζήτηση (quadratic search), που σκοπό έχει τη γρήγορη απομάκρυνση των κλειδιών από την αρχική περιοχή σύγκρουσης. Σύμφωνα με τη μέθοδο αυτή οι επόμενες θέσεις που θα εξετασθούν μπορούν να υπολογισθούν με βάση τη σχέση:

( $c_{1}\ i^{2}+c_{2}\ i+{\tt key}\mod m)\ \mod\ m$

όπου $i$ είναι ο αύξων αριθμός της αναζήτησης (δηλαδή, $i=0,1,2,\ldots$ ), ενώ τα $c_{1}$ και $c_{2}$ είναι αυθαίρετες σταθερές.

Στο Σχήμα 7.15 παρουσιάζεται η εισαγωγή της προηγούμενης ομάδας κλειδιών στον πίνακα των 11 θέσεων θεωρώντας ότι $c_{1}$ =1 και $c_{2}$ =2. Είναι εύκολη για τον αναγνώστη η κατανόηση του τρόπου που προκύπτουν οι διαδοχικές μορφές που παίρνει ο πίνακας μετά την αποθήκευση των κλειδιών 71, 56, 10 και 90, αντίστοιχα. Σημειώνεται ότι τα κλειδιά 56, 5 και 19 εισάγονται μετά από 2, 3, και 3 προσπάθειες, αντίστοιχα.

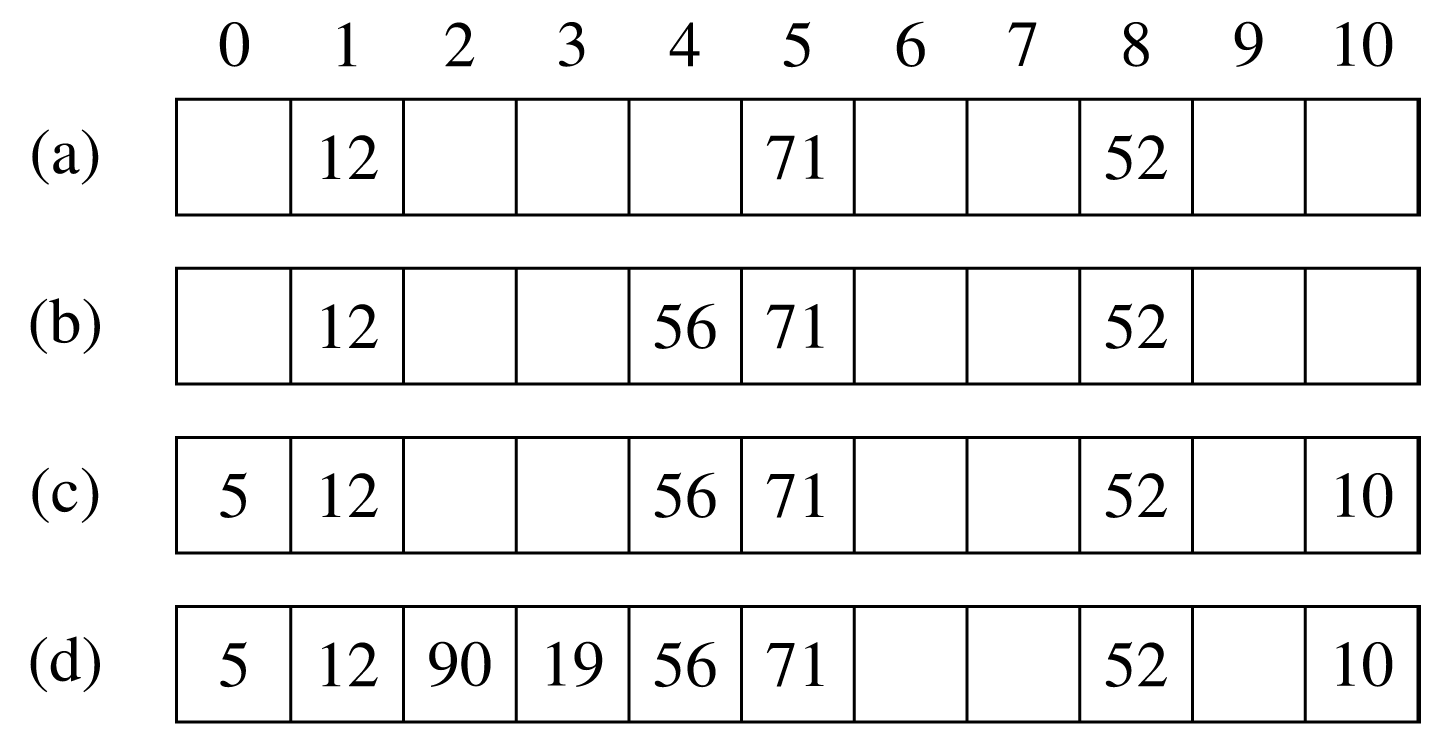
Σχήμα 7.15: Τετραγωνικός κατακερματισμός.

Επίσης, σημειώνεται ότι η προηγούμενη γενική σχέση μπορεί να απλοποιηθεί ως εξής:

(i^{2}+{\tt key}\mod m)\mod m

(7.17)

Για την περίπτωση αυτή έχει αποδειχθεί ότι δεν είναι απαραίτητο να υπολογίζεται το τετράγωνο που είναι χρονοβόρα πράξη, αλλά η θέση όπου θα γίνει η $i$ -οστή σύγκριση μπορεί να προκύψει προσθέτοντας 2 μονάδες στο άλμα, που χρησιμοποιήθηκε στην ( $i-1$ )-οστή σύγκριση. Αυτό φαίνεται από την επόμενη ταυτότητα, που μπορεί να αποδειχθεί με μαθηματική επαγωγή:

1+3+5+...+(2i-1)\ =\ i^{2}

(7.18)

Στη συνέχεια δίνεται η διαδικασία εισαγωγής με την τετραγωνική εξέταση, που στηρίζεται στην αντίστοιχη διαδικασία της γραμμικής εξέτασης. Είναι εύκολο για τον αναγνώστη να μετατρέψει τη διαδικασία search της γραμμικής εξέτασης, ώστε να ισχύει για την τετραγωνική εξέταση.

Algorithm Quadratic_Insert(

k e y

)

location=Hash(key)

2. if

A[location]==0

then

A[location]=key

; return TRUE

4. else

count=0

;

increment=1

6. repeat

count=count+1

location=(location+increment)\mod{m}

increment=increment+2

10. until

(A[location]==0)

(count==m\div 2)

11. if

A[location]==0

then

12.

A[location]=key

; return TRUE

13. else return FALSE

Σχήμα 7.16: Η διαδικασία ένθεσης ενός στοιχείου

k e y

στον τετραγωνικό κατακερματισμό.

Ένα μειονέκτημα της μεθόδου αυτής είναι ότι για μερικές τιμές του μεγέθους του πίνακα υπάρχει πιθανότητα να καταστεί αδύνατη η εισαγωγή ενός κλειδιού. Ειδικά αν $m=2^{k}$ , τότε μπορεί να προσπελασθούν πολύ λίγες θέσεις του πίνακα, ενώ διαφορετική είναι η περίπτωση όπου το $m$ είναι πρώτος αριθμός. Στην περίπτωση αυτή μπορεί η $i$ -οστή εξέταση να συμπίπτει με την ( $m-i$ )-οστή εξέταση.

Πρόταση 7.10.

Αν το $m$ είναι πρώτος αριθμός, τότε κατά την τετραγωνική εξέταση μπορεί να προσπελασθούν μόνο οι μισές θέσεις του πίνακα.

Απόδειξη. Έστω ότι η $i$ -οστή και η $j$ -οστή προσπάθεια, όπου το $j$ είναι ο μικρότερος τέτοιος ακέραιος, συμπίπτουν στην ίδια θέση του πίνακα. Τότε ισχύει:

(h+i^{2})\mod m\ =\ (h+j^{2})\mod m

(7.19)

Συνεπώς, προκύπτει:

(j-i)\times(j+i)\ =\ 0\mod m

(7.20)

Επειδή τα $j$ και $i$ είναι άνισα, πρέπει να ισχύει:

(j+i)\ =\ 0\mod m

(7.21)

Άρα, πρέπει ή το $i$ ή το $j$ είναι μεγαλύτερα από $m$ /2.

Επειδή ισχύει η προηγούμενη πρόταση ο πίνακας θεωρείται πλήρης, όταν ισχύει $2n=m$ . (όπως φαίνεται στα όρια της εντολής ελέγχου until της εντολής 10.) Το πρόβλημα αυτό της τετραγωνικής εξέτασης επιλύεται μερικώς με την πρόσθεση διαδοχικά των όρων της ακολουθίας +1, –1, +4, –4, +9, –9 κλπ. επάνω στην αρχική ποσότητα της location (εντολή 1) και με κατάλληλη αναγωγή στο μέγεθος του πίνακα.

7.4.3 Διπλός Κατακερματισμός

Η τετραγωνική αναζήτηση αντιμετωπίζει το πρόβλημα της πρωτεύουσας συγκέντρωσης, υποφέρει όμως από τη λεγόμενη δευτερεύουσα συγκέντρωση (secondary clustering). Ο λόγος είναι είτε ο τρόπος επιλογής της επόμενης θέσης, ο οποίος είναι κοινός για όλα τα κλειδιά, είτε η εξάρτηση από την αρχική διεύθυνση, όπου κατευθύνεται ένα κλειδί προς αποθήκευση. Το πρόβλημα αυτό αντιμετωπίζεται με την τεχνική του διπλού κατακερματισμού (double hashing), που χρησιμοποιεί μία δεύτερη συνάρτηση μετασχηματισμού για να εντοπίσει την επόμενη διαθέσιμη θέση. Δηλαδή, έστω ότι χρησιμοποιείται η συνάρτηση της διαίρεσης:

h_{1}({\tt key})\ =\ {\tt key}\mod m

(7.22)

για την εύρεση της αρχικής θέσης αποθήκευσης του κλειδιού. Σε περίπτωση σύγκρουσης χρησιμοποιείται μία άλλη συνάρτηση, για να δώσει την απόσταση σε θέσεις από την αρχική θέση. Σε περίπτωση νέας σύγκρουσης γίνεται δοκιμή σε θέση που απέχει την ίδια απόσταση από τη θέση της δεύτερης σύγκρουσης. Ένα συνηθισμένο παράδειγμα συνάρτησης επανα-κατακερματισμού είναι:

h_{2}({\tt key})\ =\ ({\tt key}\div m)\mod m

(7.23)

Δηλαδή, στη δεύτερη αυτή συνάρτηση πρώτα υπολογίζεται το πηλίκο του κλειδιού διαιρούμενου με το μήκος του πίνακα, κατόπιν υπολογίζεται το υπόλοιπο (κατά τα γνωστά) που προστίθεται στο αποτέλεσμα της $h_{1}$ (key). Σημειώνεται ότι αν το υπολογιζόμενο πηλίκο είναι ίσο με 0, τότε αυθαίρετα εξισώνεται με 1. Έτσι, με τον τρόπο αυτό τα συνώνυμα που συγκρούονται σε μία αρχική θέση δεν ακολουθούν την ίδια διαδρομή στον πίνακα για την εύρεση μίας διαθέσιμης θέσης. Πρέπει επίσης να προσεχθεί, ώστε το μέγεθος του πίνακα να είναι πρώτος αριθμός, γιατί αλλιώς για μερικά κλειδιά υπάρχει η δυνατότητα να μην προσπελασθούν όλες οι θέσεις του πίνακα για εξέταση. Από τα προηγούμενα γίνεται αντιληπτό γιατί η μέθοδος αυτή λέγεται και μέθοδος γραμμικού πηλίκου (linear quotient).

Ας εξετασθεί και πάλι το παράδειγμα εισαγωγής με τις γνωστές τιμές κλειδιών. Στο Σχήμα 7.17 φαίνεται διαδοχικά η μορφή του πίνακα μετά την εισαγωγή των κλειδιών 71, 56, 10 και 90, αντίστοιχα.

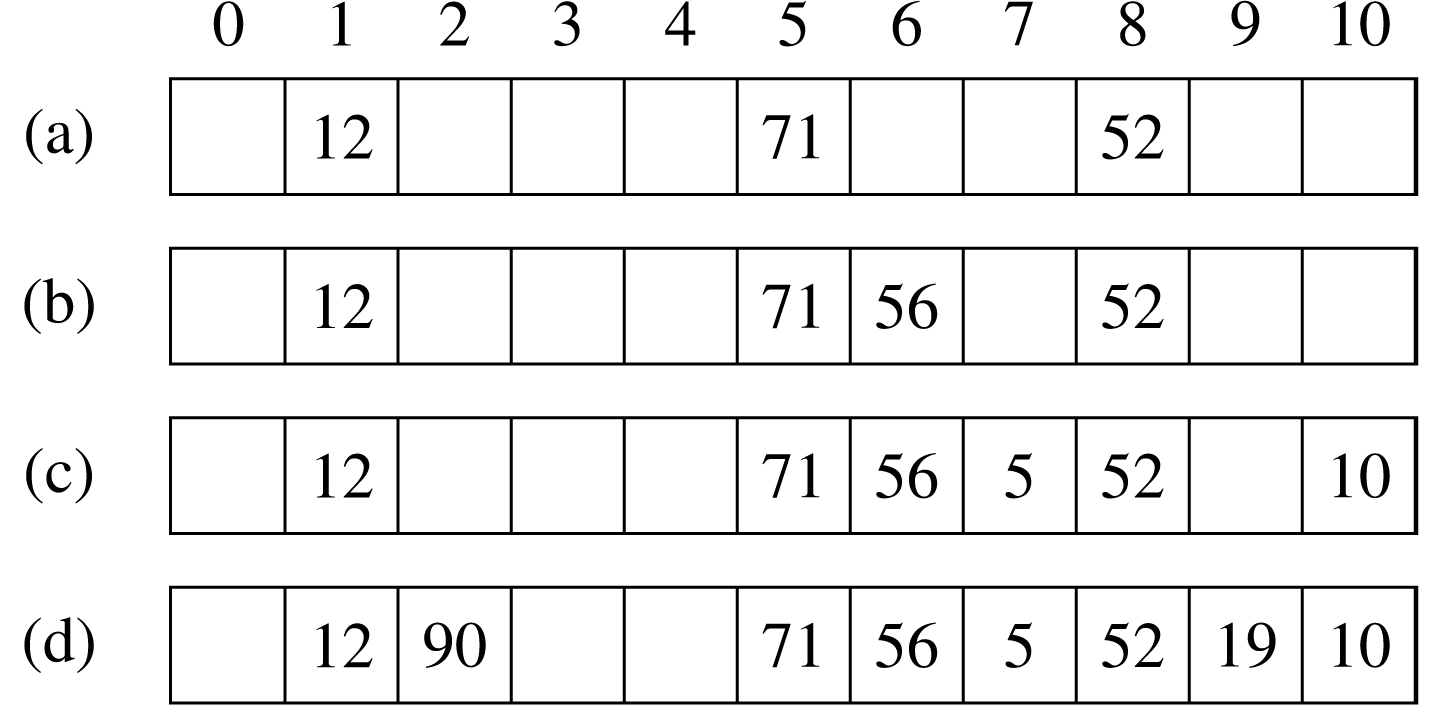
Στη συνέχεια, δίνεται η διαδικασία double_insert για την εισαγωγή στοιχείων σε πίνακα με τη μέθοδο του διπλού κατακερματισμού. Με hash1 και hash2 συμβολίζονται οι δύο συναρτήσεις κατακερματισμού που περιγράφηκαν προηγουμένως.

Algorithm Double_Insert(

k e y

)

location=hash1(key)

2. if

A[location]==0

then

A[location]=key

; return TRUE

4. else

increment=hash2(key)

last=(location+(n-1)\cdot increment)\mod{m}

7. repeat

location=(location+increment)\mod{m}

8. until

(A[location]==0)

(location==last)

9. if

A[location]==0

then

10.

A[location]=key

; return TRUE

11. else return FALSE

Σχήμα 7.18: Η διαδικασία ένθεσης ενός στοιχείου

k e y

στον διπλό κατακερματισμό.

Πρόταση 7.11.

Η μέση τιμή του αριθμού των συγκρίσεων για την επιτυχή και την ανεπιτυχή αναζήτηση σύμφωνα με τη μέθοδο του διπλού κατακερματισμού είναι αντίστοιχα:

	$\displaystyle{\rm E}$	$\displaystyle\approx$	$\displaystyle-\ \frac{\ln(1-a)}{a}$
	$\displaystyle{\rm A}$	$\displaystyle\approx$	$\displaystyle\frac{1}{1-a}$

Απόδειξη. Η πιθανότητα κάποια θέση να είναι κατειλημμένη είναι $a$ . Επομένως, για την ανεπιτυχή αναζήτηση ισχύει:

	$\displaystyle{\rm A}$	$\displaystyle=$	$\displaystyle\sum_{k=1}^{m}k\ a^{k-1}\ (1-a)\ =\ \sum_{k=1}^{m}k\ a^{k-1}\ -\ % \sum_{k=1}^{m}k\ a^{k}$
		$\displaystyle=$	$\displaystyle\sum_{k=1}^{m}a^{k-1}-m\ a^{m}$

Αν το $m$ είναι πολύ μεγάλο, τότε ο αφαιρετέος είναι πολύ μικρός, ενώ το άθροισμα μπορεί να θεωρηθεί ως άθροισμα απείρων όρων φθίνουσας ακολουθίας. Έτσι, προκύπτει η αλήθεια της πρότασης.

Ο αριθμός των συγκρίσεων για μία επιτυχή αναζήτηση ισούται με τον αριθμό των συγκρίσεων για την εισαγωγή του αντίστοιχου κλειδιού. Αν θεωρηθεί ότι ο πίνακας δημιουργείται εισάγοντας τα κλειδιά ένα-προς-ένα, τότε ο παράγοντας φόρτωσης αυξάνει κατά μικρά βήματα. Άρα, η τιμή του E ισούται με το μέσο όρο των τιμών του A, καθώς ο παράγοντας φόρτωσης αυξάνει από 0 ως $a$ . Συνεπώς:

{\rm E}\ =\ \frac{1}{a}\int_{0}^{a}Α\ {\rm d}a\ =\ \frac{1}{a}\int_{0}^{a}% \frac{1}{1-a}\ {\rm d}a

(7.24)

από όπου προκύπτει η αντίστοιχη αλήθεια της πρότασης.

7.4.4 Κατακερματισμός με Αλυσίδες

Αναφέραμε ότι η οικογένεια των μεθόδων του κλειστού κατακερματισμού δεν χρησιμοποιεί επιπλέον χώρο πέραν του χώρου του συγκεκριμένου πίνακα. Μία άλλη μεγάλη οικογένεια μεθόδων κατακερματισμού, η οικογένεια της ανοικτής διεύθυνσης (open addressing), χρησιμοποιεί αλυσίδες που ξεκινούν από τις $m$ θέσεις του πίνακα και μπορούν να επεκταθούν δυναμικά. Σε επίπεδο τύπων υποθέτουμε ότι υπάρχει μία δομή record με δύο πεδία, όπου το πρώτο πεδίο data αφορά στα καθαρά δεδομένα, ενώ το δεύτερο πεδίο ptr παριστά το δείκτη προς τον επόμενο κόμβο της αλυσίδας. Το διπλανό σχήμα δείχνει ένα παράδειγμα της δομής αυτής με $m=11$ και $n=8$ (τα ίδια κλειδιά με το προηγούμενο παράδειγμα). Πιο συγκεκριμένα, πρέπει να έχουμε υπ’όψιν ότι η παραλλαγή αυτή λέγεται μέθοδος με ξεχωριστές αλυσίδες (separate chaining), καθώς υπάρχει και η μέθοδος των σύμφυτων αλυσίδων (coalesced chaining), η οποία όμως δεν θα μας απασχολήσει στη συνέχεια. Ο ψευδοκώδικας Chain_Search που ακολουθεί δείχνει τη διαδικασία επιτυχούς και ανεπιτυχούς αναζήτησης.

Σχήμα 7.19: Κατακερματισμός με αλυσίδες.

Algorithm Chain_Search(

k e y

)

address=hash(key)

;

j=A[address]

2. while

(j\neq nil)

3. if

(j.data==key)

then return TRUE

4. else

j=j.ptr

5. return FALSE

Σχήμα 7.20: Η διαδικασία εύρεσης ενός στοιχείου

k e y

στον κατακερματισμό με αλυσίδες.

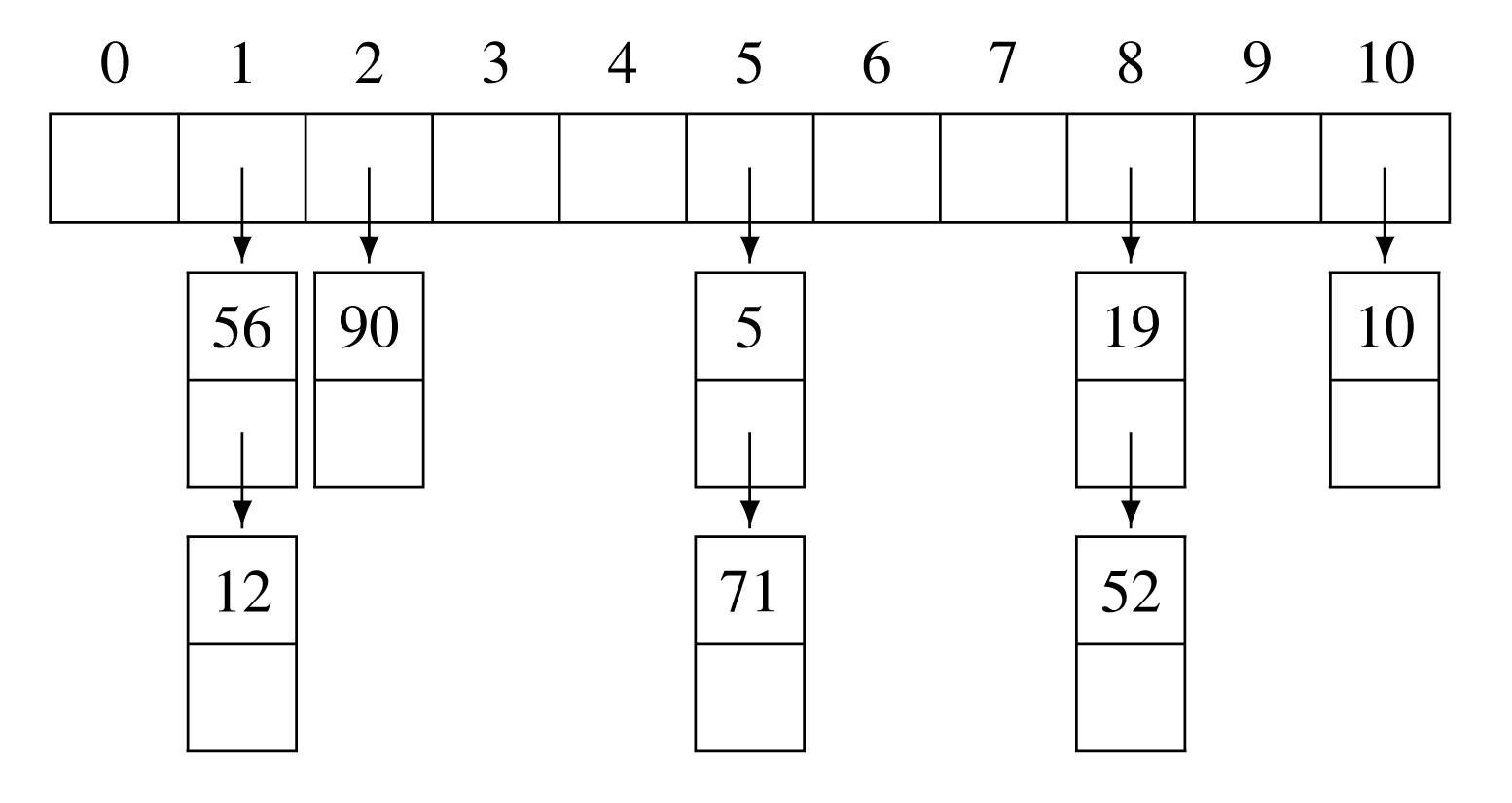
Πρόταση 7.12.

Η μέση τιμή του αριθμού των συγκρίσεων κατά την αναζήτηση σε κατρακερματισμό με αλυσίδες, σε περίπτωση επιτυχούς και ανεπιτυχούς αναζήτησης είναι αντιστοίχως:

{\rm E}\ =\ 1+\frac{\alpha}{2}-\frac{1}{2m}

(7.25)

και

{\rm A}\ \approx\ 1+\alpha

(7.26)

Απόδειξη. Θα εξετάσουμε κατ’αρχάς την περίπτωση της ανεπιτυχούς αναζήτησης. Υποθέτοντας μία τυχαία συνάρτηση κατακερματισμού, αναμένουμε ότι κάθε κλειδί θα κατευθυνθεί σε οποιαδήποτε θέση από τις $m$ θέσεις του πίνακα με την ίδια πιθανότητα $1/m$ (εντολή 1). Στη συνέχεια, η αναζήτηση θα συνεχισθεί στην αντίστοιχη αλυσίδα (εντολές 3-5), που θα τη διασχίσει μέχρι το τέλος της, ώστε να επιστραφεί η ένδειξη false. Επομένως, η επίδοση εξαρτάται από το μήκος της αλυσίδας, και εφόσον συνολικά έχουν εισαχθεί $n$ κλειδιά σε όλες τις $m$ αλυσίδες, έπεται ότι το μέσος μήκος της αλυσίδας είναι $n/m=\alpha$ . Άρα, η πολυπλοκότητα της ανεπιτυχούς αναζήτησης είναι Θ(1+ $\alpha$ ) στη μέση περίπτωση.

Για να εξετάσουμε την περίπτωση της επιτυχούς αναζήτησης, θα υποθέσουμε ότι κάθε νέο κλειδί εισάγεται στο τέλος της αντίστοιχης αλυσίδας. Επομένως, το πλήθος των προσπελάσεων που θα πραγματοποιηθούν για μία επιτυχή αναζήτηση είναι μία μονάδα περισσότερο από το πλήθος που απαιτούνται για την εισαγωγή του αντίστοιχου κλειδιού. Όταν εισάγεται το $i$ -οστό κλειδί, το μήκος της αντίστοιχης αλυσίδας είναι $(i-1)/m$ . Επομένως, ισχύει:

	$\displaystyle{\rm E}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\ \sum_{i=1}^{n}\left(1+\frac{i-1}{m}\right)\ =\ 1+% \frac{1}{nm}\sum_{i=1}^{n}(i-1)$
		$\displaystyle=$	$\displaystyle 1+\frac{1}{nm}\ \frac{(n-1)n}{2}\ =\ 1+\frac{\alpha}{2}-\frac{1}% {2m}$

Συνεπώς και πάλι προκύπτει ότι η πολυπλοκότητα είναι Θ( $1+\alpha$ ) στη μέση περίπτωση.

Στο σημείο αυτό πρέπει να προσεχθεί ότι στην περίπτωση της ανοικτής διεύθυνσης ισχύει $\alpha\leq 1$ , αλλά στην περίπτωση των αλυσίδων δεν ισχύει αυτός ο περιορισμός. Επομένως, η επίδοση της επιτυχούς και της ανεπιτυχούς αναζήτησης είναι ικανοποιητική, όταν το $n$ είναι της τάξης του $m$ , επομένως το $\alpha$ είναι της τάξης της μονάδας.

7.5 Βιβλιογραφική Συζήτηση

Η δυαδική αναζήτηση απασχόλησε τους ερευνητές της Πληροφορικής στις αρχές της δεκαετίας του 1970. Οι πρώτες αναλύσεις της μεθόδου αναφέρονται στα άρθρα [48, 83]. Την περίοδο εκείνη η μέθοδος ήταν δημοφιλής και εκδοχές της δημοσιεύονταν σε πλήθος βιβλίων και άρθρων. Ωστόσο, τότε δεν ήταν προφανές αυτό που είναι σήμερα. Στο άρθρο [98] παρουσιάζονται και αναλύονται τα λάθη που είχαν παρεισφρήσει σε 26 δημοσιεύσεις της εποχής σχετικά με το θέμα. Εξάλλου ο Bentley ισχυρίζεται ότι λίγοι προγραμματιστές μπορούν να κωδικοποιήσουν τη μέθοδο χωρίς λάθη μέσα σε δύο ώρες [13]. Γενικεύσεις της μεθόδου μπορούν να βρεθούν στα άρθρα [55, 97].

Δημοφιλής μέθοδος αναζήτησης υπήρξε και η αναζήτηση με παρεμβολή. Προτάθηκε το 1977 από τους Perl-Reingold [147] και εν συνεχεία μελετήθηκε στα άρθρα [25, 62, 100, 146], αυτή καθώς και οι παραλλαγές της με σειριακή αναζήτηση [63] και με δυαδική αναζήτηση [158]. Οι παραλλαγές Alternate και Retrieve διαπτυπώθηκαν από τον Willard [198].

Πέραν των δύο αυτών μεθόδων, στη βιβλιογραφία αναφέρονται και άλλες μέθοδοι, που όμως δεν άντεξαν στο χρόνο. Για παράδειγμα, αναφέρεται η Fibonaccian μέθοδος [46, 138], η αναζήτηση άλματος [172, 82] και η πολυωνυμική αναζήτηση [171].

Η μέθοδος του κατακερματισμού υπήρξε εξίσου δημοφιλής και ερευνήθηκε σε βάθος τις δεκαετίες του 1970 και 1980. Οι πρώτες βασικές εργασίες σχετικά με τον κατακερματισμό ήταν τα άρθρα [118, 148]. Σχετικά με την επιλογή της κατάλληλης συνάρτησης κατακερματισμού είναι τα άρθρα [87, 122]. Θεμελιωτές της τετραγωνικής μεθόδου ήταν οι Bell και Radke [10, 151], ενώ αντίστοιχα στο διπλό κατακερματισμό αναφέρονται τα άρθρα [71, 108]. Κατά καιρούς έχουν εμφανισθεί διάφορες επισκοπήσεις της περιοχής, όπως τα άρθρα [37, 103, 117, 168]. Το βιβλίο των Gonnet-BeazaYates συμπεριλαμβάνει σε συνοπτικό τρόπο πλήθος μεθόδων κατακερματισμού και αντίστοιχες αναλύσεις [60]. Τη δεκαετία του 1990 η έρευνα στράφηκε στη σχεδίαση δυναμικών μεθόδων κατακερματισμού για χρήση σε δευτερεύουσα μνήμη και προέκυψαν πολλές νέες μέθοδοι. Οι μέθοδοι αυτές δεν θα εξετασθούν στα πλαίσια του βιβλίου αυτού, καθώς ταιριάζουν περισσότερο στο αντικείμενο των Βάσεων Δεδομένων (Data Bases). Ωστόσο, ο ενδιαφερόμενος αναγνώστης παραπέμπεται στην επισκόπηση [41].

Η Άσκηση 4 βασίζεται στο άρθρο [50], η Άσκηση 7 στο άρθρο [18], η Άσκηση 9 στο άρθρο [56], η Άσκηση 10 στα άρθρα [109, 110], η Άσκηση 11 στο άρθρο [105], ενώ η Άσκηση 12 στο άρθρο [5].

7.6 Ασκήσεις

1.

Να βρεθεί η μέση τιμή του αριθμού των αναζητήσεων για την περίπτωση της ανεπιτυχούς σειριακής αναζήτησης σε ταξινομημένο πίνακα. Να θεωρηθεί ότι η πιθανότητα αναζήτησης ενός ανύπαρκτου κλειδιού από τα δημιουργούμενα διαστήματα μεταξύ των κλειδιών είναι ίση για όλα τα διαστήματα.
2.

Δίνεται ταξινομημένος πίνακας με $n$ στοιχεία, όπου επιτρέπεται η ύπαρξη πολλαπλών τιμών. Να τροποποιηθεί ο αλγόριθμος της δυαδικής αναζήτησης, ώστε να βρίσκει την πρώτη εμφάνιση του αναζητούμενου κλειδιού σε χρόνο της τάξης Θ $(\log n)$ .
3.

Δίνεται ταξινομημένος πίνακας με $n$ στοιχεία, όπου επιτρέπεται η ύπαρξη πολλαπλών τιμών. Να τροποποιηθεί ο αλγόριθμος της δυαδικής αναζήτησης, ώστε να βρίσκει το μεγαλύτερο κλειδί που είναι μικρότερο από το αναζητούμενο κλειδί, το οποίο όμως δεν υπάρχει (ανεπιτυχής αναζήτηση). Αν το αναζητούμενο είναι το μικρότερο στοιχείο του πίνακα, τότε να επιστρέφεται μήνυμα λάθους.
4.

Η μέθοδος των παραγεμισμένων λιστών (padded lists) προσπαθεί να βελτιώσει τη δυαδική αναζήτηση χρησιμοποιώντας δύο πίνακες ίσου μεγέθους: ένα πίνακα για δεδομένα και ένα πίνακα για λογικές σημαίες. Αρχικά ο πίνακας δεδομένων περιέχει και κάποιες κενές θέσεις ομοιόμορφα διαμοιρασμένες μεταξύ των κατειλημμένων θέσεων. Στις κενές αυτές θέσεις αποθηκεύονται τυχαίες τιμές, έτσι ώστε ο πίνακας να παραμένει ταξινομημένος, ενώ οι αντίστοιχες θέσεις του πίνακα σημαιών παίρνουν τιμές false. Η αναζήτηση ενός κλειδιού γίνεται στον πίνακα δεδομένων κατά τα γνωστά, αλλά παράλληλα ελέγχεται αν η αντίστοιχη λογική σημαία είναι true. Σε περίπτωση διαγραφής η σημαία από true γίνεται false. Τέλος, αν σε περίπτωση εισαγωγής η θέση δεν είναι κατειλημμένη, τότε η σημαία από false γίνεται true, ενώ αν η θέση είναι κατειλημμένη, τότε ακολουθείται μία διαδικασία ολισθήσεων. Για μεγαλύτερη αποτελεσματικότητα περιοδικά απαιτείται η αναδιοργάνωση των πινάκων, έτσι ώστε οι κενές θέσεις να μοιράζονται και πάλι ομοιόμορφα μεταξύ των κατειλημμένων θέσεων. Να σχεδιασθούν και να αναλυθούν αλγόριθμοι υλοποίησης των διαφόρων λειτουργιών των παραγεμισμένων λιστών (δηλαδή, εισαγωγή, διαγραφή, αναζήτηση).
5.

Με βάση την δυαδική αναζήτηση να σχεδιασθεί και να αναλυθεί μέθοδος αναζήτησης σε ταξινομημένο πίνακα που να τον τριχοτομεί (αντί να τον διχοτομεί).
6.

Ποιά είναι η πιθανότητα 3 άτομα μεταξύ 100 τυχαίων ατόμων να έχουν γενέθλια την ίδια ημέρα;
7.

Έστω ένας πίνακας με $n$ ταξινομημένα στοιχεία, όπου $n=i\times j$ . Έτσι, χωρίζουμε τον πίνακα σε $i$ υποπίνακες με $j$ στοιχεία ο καθένας. Προκειμένου να ψάξουμε ένα κλειδί πρώτα το συγκρίνουμε με σειριακό τρόπο με το τελευταίο κλειδί του κάθε υποπίνακα. Με τον τρόπο αυτό καταλαβαίνουμε σε ποιόν υποπίνακα πρέπει να συνεχισθεί η αναζήτηση. Σε περίπτωση επιτυχούς αναζήτησης, στη χειρότερη περίπτωση θα εκτελεσθούν $i+j$ συγκρίσεις, στη μέση περίπτωση θα εκτελεσθούν $\frac{i+1}{2}+\frac{j+1}{2}$ συγκρίσεις. Για ποιές τιμές των $i, j$ η επίδοση βελτιστοποιείται;
8.

Στη συνέχεια δίνεται η διαδικασία αναζήτησης Fibonacci. Υποτίθεται ότι αναζητείται το key στον ταξινομημένο πίνακα A[0..n-1]. Αν το κλειδί βρεθεί, τότε η μεταβλητή position επιστρέφει τη θέση του, αλλιώς επιστρέφει 0. Σημειώνεται, επίσης, ότι η εντολή while υπολογίζει τον αριθμό Fibonacci που είναι αμέσως μεγαλύτερος του n. Να αναλυθεί η πολυπλοκότητα του αλγορίθμου.
```
procedure Fibonacci(key,position)
j<--1;
while F(j)<n+1 do j<--j+1;
done <-- false;
mid <-- n-F(j-2)+1; f1 <-- F(j-2); f2 <-- F(j-3);
while (not done) and (key<>A[mid]) do
   if (mid<=0) or (key>A[mid]) then
       if f1=1 then
          done <-- true;
       else
          mid <-- mid+f2; f1 <-- f1-f2; f2 <-- f2-f1;
   else if f2=0 then done <-- true;
   else
       mid <-- mid-f2; temp <-- f1-f2; f1 <-- f2; f2 <-- temp;
if done then position <-- 0 else position <-- mid
```
9.

Έστω ένας πύργος με $n$ ορόφους, ενώ επίσης μας δίνεται μία λάμπα και πρέπει να βρούμε το χαμηλότερο όροφο από τον οποίο θα σπάσει, αν την αφήσουμε σε ελεύθερη πτώση. Η πρώτη λύση είναι να αρχίσουμε από τον πρώτο όροφο και να συνεχίσουμε προς το δεύτερο, τρίτο κλπ μέχρι να βρούμε την απάντηση. Προφανώς η λύση αυτή έχει γραμμική πολυπλοκότητα. Να σχεδιασθούν δύο αλγόριθμοι μη γραμμικής πολυπλοκότητας για την εύρεση της αντοχής της λάμπας, ενώ μας διατίθενται δύο λάμπες για την εκτέλεση του πειράματος. Να αποδειχθεί η πολυπλοκότητα του κάθε αλγορίθμου.
10.

Συχνά παρουσιάζεται η ανάγκη αναζήτησης $k$ κλειδιών σε ένα ταξινομημένο πίνακα $n$ στοιχείων. Να σχεδιασθούν και να αναλυθούν τρεις αλγόριθμοι μαζικής αναζήτησης, όπου δηλαδή τα κλειδιά να αναζητούνται με μία κλήση του αλγορίθμου και όχι με διαδοχικές $k$ κλήσεις. Οι τρεις αλγόριθμοι να στηρίζονται στη σειριακή, τη δυαδική και την αναζήτηση παρεμβολής.
11.

Η γραμμική αναζήτηση με διαχωρισμό της ακολουθίας (split sequence linear search) λειτουργεί ως εξής. Έστω ότι κατά την εισαγωγή ενός κλειδιού key εφαρμόζεται η συνάρτηση κατακερματισμού hash(key) και προκύπτει μία θέση $i$ του πίνακα, η οποία όμως είναι κατειλημμένη. Αν το κλειδί που είναι αποθηκευμένο στη θέση $i$ είναι μεγαλύτερο (μικρότερο) από το αναζητούμενο κλειδί, τότε η επόμενη θέση όπου θα συνεχισθεί η σύγκριση δίνεται αντίστοιχα από τις σχέσεις:

$({\tt hash(key)+c_{1})\mod m}\ \ \ \ {\rm και}\ \ \ \ ({\tt hash(key)+c_{2})% \mod m}$ (7.27)

όπου τα ${\tt c_{1}}$ και ${\tt c_{2}}$ είναι δύο άνισες ακέραιες σταθερές. Έτσι, δημιουργούνται δύο ακολουθίες θέσεων, όπου θα κατευθυνθούν τα συνώνυμα και η πρωτεύουσα συγκέντρωση πράγματι μειώνεται. Να σχεδιασθεί η μέθοδος στις λεπτομέρειές της (δηλαδή, εισαγωγή, διαγραφή, αναζήτηση) και να αναλυθεί η χειρότερη περίπτωσή της.
12.

Ο ταξινομημένος κατακερματισμός (ordered hashing) μπορεί να εφαρμοσθεί τόσο με τη γραμμική και τη μη γραμμική αναζήτηση, όσο και με το διπλό κατακερματισμό. Σύμφωνα με τη μέθοδο αυτή όταν προκύπτει σύγκρουση κατά την εισαγωγή, τότε τη συγκεκριμένη θέση καταλαμβάνει το κλειδί με τη μικρότερη τιμή εκτοπίζοντας το κλειδί με τη μεγαλύτερη τιμή, το οποίο πρέπει να επανα-εισαχθεί. Να σχεδιασθούν οι αλγόριθμοι εισαγωγής, διαγραφής και αναζήτησης. Να αναλυθεί η επιτυχής και η ανεπιτυχής αναζήτηση για την περίπτωση του ταξινομημένου διπλού κατακερματισμού.
13.

Αν είναι γνωστή εκ των προτέρων η πιθανότητα αναζήτησης κάθε κλειδιού, τότε να σχεδιασθεί και να αναλυθεί η διαδικασία εισαγωγής, διαγραφής και αναζήτησης για μία παραλλαγή για τη μέθοδο κατακερματισμού με αλυσίδες, η οποία να εκμεταλλεύεται αυτό το γεγονός.