Σχεδίαση και Ανάλυση Αλγορίθμων 1 Εισαγωγή 3 Γεννήτριες Συναρτήσεις

Κεφάλαιο 2Θεωρητικό Υπόβαθρο

Στο κεφάλαιο αυτό θα εξετασθούν τρία αντικείμενα. Πρώτον, θα παρουσιασθούν επί τροχάδην μερικά βασικά μαθηματικά εργαλεία που είναι απαραίτητα κατά την ανάλυση των αλγορίθμων. Πολλά από αυτά θα χρησιμοποιηθούν σε επόμενα κεφάλαια του βιβλίου. Δεύτερον, θα εισαχθούν με τυπικό τρόπο οι έννοιες της πολυπλοκότητας και των συμβολισμών Ο, Ω, Θ, ο και ω, που αναφέρθηκαν ακροθιγώς στο προηγούμενο κεφάλαιο. Τρίτον, θα γίνει μία πρώτη χρήση των μαθηματικών εργαλείων και των συμβολισμών στην πράξη για την μεθοδικότερη ανάλυση μερικών απλών αλγορίθμων.

2.1 Μαθηματικά Εργαλεία

Συνάρτηση Πάτωμα και Συνάρτηση Οροφή

Δεδομένου πραγματικού αριθμού $x$ , το $\lfloor x\rfloor$ ισούται με το ακέραιο μέρος του $x$ , ενώ το $\lceil x\rceil$ ισούται με τον μεγαλύτερο (ή ίσο) ακέραιο αριθμό του $x$ . Για τις συναρτήσεις αυτές ισχύουν οι εξής ιδιότητες (όπου τα $n, a, b$ ακέραιοι):

x-1\ \leq\ \lfloor x\rfloor\ \leq\ x\ \leq\ \lceil x\rceil\ \leq\ x+1

(2.1)

\lfloor n/2\rfloor+\lceil n/2\rceil\ =\ n

(2.2)

\left\lceil\frac{\lceil n/a\rceil}{b}\right\rceil\ =\ \left\lceil\frac{n}{ab}% \right\rceil\hskip 56.905512pt\left\lfloor\frac{\lfloor n/a\rfloor}{b}\right% \rfloor\ =\ \left\lfloor n/ab\right\rfloor

(2.3)

Εκθετικά και Δυνάμεις

Για τους πραγματικούς αριθμούς $a\neq 0,m,n$ ισχύουν οι εξής βασικές ιδιότητες:

a^{0}=1\hskip 19.916929pta^{1}=a\hskip 19.916929pta^{-1}=1/a\hskip 19.916929pt% (a^{m})^{n}=a^{mn}=(a^{n})^{m}\hskip 19.916929pta^{m}a^{n}=a^{m+n}

(2.4)

Για πραγματικές σταθερές $a>0,b$ ισχύει:

\lim_{n\rightarrow\infty}\frac{n^{b}}{a^{n}}\ =\ 0

(2.5)

Για κάθε πραγματικό αριθμό $x$ ισχύει:

e^{x}\ =\ 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\ldots\ =\ \sum_{i=0}^{\infty}% \frac{x^{i}}{i!}\geq 1+x

(2.6)

Για $|x|\leq 1$ ισχύει:

1+x\leq e^{x}\ \leq\ 1+x+x^{2}

(2.7)

Τέλος, ισχύει:

\lim_{n\rightarrow\infty}\left(1+\frac{x}{n}\right)\ =\ e^{x}

(2.8)

όπου $e\approx 2,71828$ , η βάση των φυσικών λογαρίθμων.

Λογάριθμοι

Για κάποιο φυσικό ή πραγματικό αριθμό $x$ , οι λογάριθμοι συμβολίζονται με $\log_{b}x$ , όπου $b$ είναι η βάση του λογάριθμου. Συνήθως, οι χρησιμοποιούμενοι λογάριθμοι αναφέρονται σε δυαδική βάση και θα δηλώνονται με $\lg x$ , ενώ οι φυσικοί/νεπέριοι λογάριθμοι θα δηλώνονται με $\ln x$ . Για τους πραγματικούς αριθμούς $a>0,b>0,c>0,n$ ισχύουν οι εξής βασικές ιδιότητες:

a=b^{\log_{b}a}\hskip 19.916929pt\log_{c}(ab)=\log_{c}a+\log_{c}b\hskip 19.916% 929pt\log_{b}a^{n}=n\log_{b}a\hskip 19.916929pt\log_{b}a=\frac{\log_{c}a}{\log% _{c}b}

(2.9)

\log_{b}(1/a)=-\log_{b}a\hskip 28.452756pt\log_{b}a=\frac{1}{\log_{a}b}\hskip 2% 8.452756pta^{\log_{b}n}=n^{\log_{b}a}

(2.10)

Σε ό,τι αφορά στις εκφράσεις με τη βοήθεια των συμβολισμών Ο, Θ κλπ. δεν έχει σημασία αν ο λογάριθμος είναι δυαδικός, νεπέριος ή οποιοσδήποτε άλλος και για το λόγο αυτό μπορεί γενικώς να χρησιμοποιείται η έκφραση $\lg$ .

Σημαντικές σχέσεις είναι οι επόμενες. Για $|x|<1$ ισχύει:

\ln(1+x)\ =\ x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+\frac{x^{5}}{5}-\ldots

(2.11)

ενώ για $x>-1$ ισχύει:

\frac{x}{1+x}\ \leq\ \ln(1+x)\ \leq\ x

(2.12)

Παραγοντικά

Είναι γνωστό ότι

n!\ =\ 1\times 2\times 3\times\cdots\times n\ =\ \prod_{i=1}^{n}i

(2.13)

Πολύ συχνά χρησιμοποιούμενος είναι ο τύπος του Stirling:

n!\ =\ \sqrt{2\pi n}\left(\frac{n}{e}\right)^{n}\left(1+\frac{1}{12n}+\frac{1}% {288n^{2}}+\ldots\right)

(2.14)

Αν απαλείψουμε την παρένθεση, τότε οδηγούμαστε σε μία πολύ καλή προσέγγιση. Για παράδειγμα, εφαρμόζοντας τον τύπο του Stirling καταλήγουμε ότι $1!\approx 0,92$ (λάθος 8%), $2!\approx 1,92$ (λάθος 4%), $5!\approx 118,02$ (λάθος 2%), ενώ για το 100! το λάθος είναι 0.08%. Με άλλα λόγια, το λάθος είναι μία φθίνουσα συνάρτηση για αυξανόμενα $n$ . Επίσης, από τον τύπο του Stirling και με απλή άλγεβρα προκύπτει ότι:

n!\ \leq\ n^{n}

(2.15)

Αριθμοί Fibonacci

Η ακολουθία αριθμών Fibonacci δεύτερης τάξης ορίζονται ως εξής:

F_{i}\ =\ F_{i-1}+F_{i-2}

(2.16)

ενώ για τις αρχικές συνθήκες ισχύει $F_{0}=0$ και $F_{1}=1$ . Άρα με βάση τον ορισμό προκύπτει ότι η σειρά των αριθμών Fibonacci είναι:

0,1,1,2,3,5,8,13,21,34,55,\ldots

(2.17)

Δεδομένης της χρυσής τομής (golden ratio), $\phi$ , και της συζυγούς τιμής, $\hat{\phi}$ , που ισούνται αντίστοιχα με:

\phi\ =\ \frac{1+\sqrt{5}}{2}\ \approx\ 1.61803\hskip 56.905512pt\hat{\phi}\ =% \ \frac{1-\sqrt{5}}{2}\ \approx\ -0.61803

(2.18)

μπορεί να αποδειχθεί επαγωγικά η ταυτότητα De Moivre:

F_{i}\ =\ \frac{\phi^{i}-\hat{\phi}^{i}}{\sqrt{5}}

(2.19)

Καθώς $|\hat{\phi}|<1$ , συνεπάγεται ότι $|\hat{\phi}|/\sqrt{5}<1/2$ . Άρα, ο $i$ -οστός αριθμός Fibonacci ισούται με $\phi^{i}/\sqrt{5}$ στρογγυλεμένο στον αμέσως μεγαλύτερο ακέραιο.

Αθροίσματα

Μερικές από επόμενες σχέσεις είναι ήδη γνωστές, αλλά τις επαναλαμβάνουμε για λόγους πληρότητας.

\sum_{i=1}^{n}i\ =\ 1+2+3+\ldots+n\ =\ \frac{1}{2}n(n+1)

(2.20)

\sum_{i=1}^{n}i^{2}\ =\ 1+2^{2}+3^{2}+\ldots+n^{2}\ =\ \frac{1}{6}n(n+1)(2n+1)

(2.21)

\sum_{i=0}^{n}x^{i}\ =\ 1+x+x^{2}+\ldots+x^{n}\ =\ \frac{x^{n+1}-1}{x-1}

(2.22)

Αν $|x|<1$ , τότε ισχύει:

\sum_{i=0}^{\infty}x^{i}\ =\ \frac{1}{1-x}

(2.23)

Παραγωγίζοντας τα δύο σκέλη της σχέσης αυτής και πολλαπλασιάζοντας επί $x$ προκύπτει:

\sum_{i=0}^{\infty}i\ x^{i}\ =\ \frac{x}{(1-x)^{2}}

(2.24)

Για τον αρμονικό αριθμό $H_{n}$ ισχύει:

H_{n}\ =\ \sum_{i=1}^{n}\frac{1}{i}\ =\ 1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac% {1}{n}\ =\ \ln n+\gamma+\frac{1}{2n}-\frac{1}{12n^{2}}+\frac{1}{120n^{4}}-\ldots

(2.25)

όπου $\gamma=0.577$ είναι η σταθερά του Euler.

Επίσης, για κάθε ακολουθία $a_{1},a_{2},\ldots,a_{n}$ ισχύουν οι σχέσεις (τηλεσκοπικά αθροίσματα):

\sum_{i=1}^{n}(a_{i}-a_{i-1})\ =\ a_{n}-a_{0}\hskip 56.905512pt\sum_{i=0}^{n-1% }(a_{i}-a_{i+1})\ =\ a_{0}-a_{n}

(2.26)

Και μία τελευταία χρήσιμη ιδιότητα με γινόμενα:

\lg\left(\prod_{i=1}^{n}a_{i}\right)\ =\ \sum_{i=1}^{n}\lg a_{i}

(2.27)

Διατάξεις, Συνδυασμοί και Δυωνυμικοί Συντελεστές

Τα $n$ στοιχεία ενός συνόλου μπορούν να παράξουν $n!$ διαφορετικές διατάξεις. Το πλήθος των δυνατών διατάξεων επιλέγοντας $k$ από $n$ είναι:

n\times(n-1)\times\ldots\times(n-(k-1))\ =\ \frac{n!}{(n-k)!}

(2.28)

Συνδυασμός των $k$ αντικειμένων από $n$ αντικείμενα είναι το πλήθος των τρόπων που μπορούν να επιλεχθούν $k$ διακριτά αντικείμενα από $n$ αντικείμενα και ισούται με:

n\choose k

(2.29)

Ο ανωτέρω τύπος προϋποθέτει ότι κάθε ένα από τα $n$ αντικείμενα μπορεί να επιλεγεί μία μόνο φορά. Ο τρόπος αυτός λέγεται επιλογή χωρίς αντικατάσταση (selection without replacement). Αντιθέτως, κατά την επιλογή με αντικατάσταση (selection with replacement) επιτρέπεται κάποιο αντικείμενο να επιλεγεί και πάλι χωρίς κάποιον περιορισμό. Για την περίπτωση αυτή, το πλήθος των επιλογών είναι:

n+k-1\choose n-1

(2.30)

Βασικές ταυτότητες των συνδυασμών (οι οποίες αποδεικνύονται εύκολα) είναι οι εξής:

{n\choose k}\ =\ \frac{n!}{k!(n-k)!}\ =\ {n\choose n-k}

(2.31)

{n\choose k}\ =\ {n-1\choose k}\ +\ {n-1\choose k-1}

(2.32)

Επίσης ισχύει:

(x+y)^{n}\ =\ \sum_{k=0}^{n}{n\choose k}x^{k}y^{n-k}

(2.33)

Αν $x=y=1$ , τότε προκύπτει ότι

2^{n}\ =\ \sum_{k=0}^{n}{n\choose k}

(2.34)

Συχνά απαιτούνται επάνω και κάτω όρια. Έτσι έχουμε:

{n\choose k}\ =\ \frac{n(n-1)\ldots(n-k+1)}{k(k-1)\ldots 1}\ =\ \frac{n}{k}\ % \frac{n-1}{k-1}\ldots\frac{n-k+1}{1}\ \geq\ \left(\frac{n}{k}\right)^{k}

(2.35)

{n\choose k}\ =\ \frac{n(n-1)\ldots(n-k+1)}{k(k-1)\ldots 1}\ \leq\ \frac{n^{k}% }{k!}\ \leq\ \left(\frac{en}{k}\right)^{k}

(2.36)

Τέλος, ο καταλανικός αριθμός ισούται με:

C_{n}\ =\ \frac{1}{n+1}\ {2n\choose k}\ =\ \frac{4^{n}}{\sqrt{\pi n^{3}}}\ % \left(1-\frac{9}{8n}+\frac{145}{128n^{2}}-\ldots\right)

(2.37)

Πιθανότητες

Από το μάθημα των Πιθανοτήτων/Στατιστικής είναι γνωστές οι επόμενες έννοιες, αλλά επίσης τις επαναλαμβάνουμε για λόγους πληρότητας. Ας υποθέσουμε ότι μία διακριτή τυχαία μεταβλητή $X$ λαμβάνει αριθμητικές τιμές: $X_{1},X_{2},X_{3},\ldots$ . Η πιθανότητα να προκύψει η τιμή $X_{i}$ συμβολίζεται με $P(X_{i})$ ή με $x x x x x$ και ισχύουν οι σχέσεις:

0\leq P(X_{i})\leq 1\hskip 56.905512pt\sum_{i=1}^{\infty}P(X_{i})\ =\ 1

(2.38)

Η μέση (ή προσδοκητή) τιμή μίας διακριτής τυχαίας μεταβλητής $X$ ισούται με:

μ = E (X) = \sum_{i = 1}^{\infty} X_{i} P (X_{i}) = \sum_{i = 1}^{\infty} P (X \geq X_{i})

(2.39)

Η απόκλιση μίας τυχαίας μεταβλητής $X$ δίνεται από τον τύπο:

\sigma^{2}\ =\ {\rm Var}[X]\ =\ {\rm E}[(X-{\rm E}[X])^{2}]\ =\ \ldots\ =\ {% \rm E}[X^{2}]-{\rm E}^{2}[X]\Rightarrow

(2.40)

{\rm E}[X^{2}]\ =\ {\rm Var}[X]-{\rm E}^{2}[X]

(2.41)

Η μέση τιμή του αθροίσματος δύο διακριτών τυχαίων μεταβλητών ισούται με:

{\rm E}(X+Y)\ =\ {\rm E}(X)+{\rm E}(Y)

(2.42)

Για δύο γεγονότα ανεξάρτητα μεταξύ τους ισχύει:

{\rm E}(X+Y)\ =\ {\rm E}(X)\ \ {\rm E}(Y)

(2.43)

Η πιθανότητα υπό συνθήκη να συμβεί ένα γεγονός $A$ δεδομένου ενός γεγονότος $B$ είναι:

p (A | B) = \frac{p (A \cap B)}{p (B)}

(2.44)

με την προϋπόθεση ότι $p(B)\neq 0$ . Έτσι, προκύπτει το Θεώρημα του Bayes:

p (A | B) = \frac{p (A) p (B | A)}{p (B)}

(2.45)

2.2 Συμβολισμοί Πολυπλοκότητας

Κατ’αρχήν παραθέτουμε τους ορισμούς τριών συμβολισμών πολυπλοκότητας (Ο, Ω και Θ), ενώ στη συνέχεια θα παραθέσουμε άλλους δύο συμβολισμούς πολυπλοκότητας (ο και ω).

Συμβολισμός Ο.
Μία συνάρτηση $f(n)$ λέγεται ότι έχει πολυπλοκότητα της τάξης O( $g(n)$ ) και συμβολίζεται με $f(n)={\rm O}(g(n))$ ή με $f(n)\in{\rm O}(g(n))$ , αν υπάρχει μία θετική σταθερά $c$ και μία τιμή $n_{0}$ , έτσι ώστε για κάθε $n>n_{0}$ να ισχύει η σχέση $f(n)<cg(n)$ . $\Box$

Σχήμα 2.1: Γραφική αναπαράσταση του $\rm O$ .

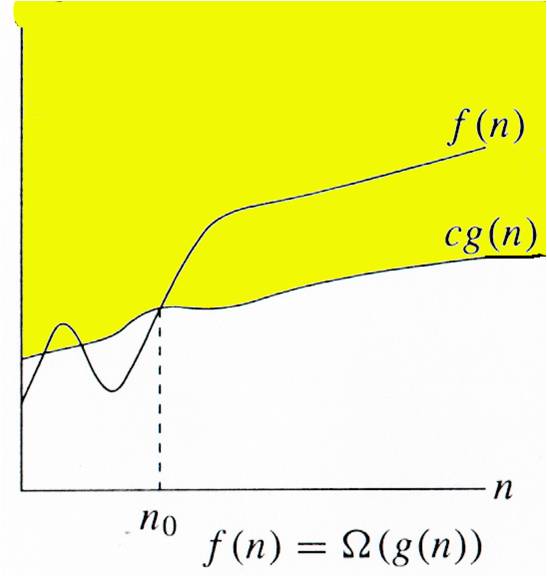
Συμβολισμός Ω.
Μία συνάρτηση $f(n)$ λέγεται ότι έχει πολυπλοκότητα της τάξης Ω( $g(n)$ ) και συμβολίζεται με $f(n)={\Omega}(g(n))$ ή με $f(n)\in{\Omega}(g(n))$ , αν υπάρχει μία θετική σταθερά $c$ και μία τιμή $n_{0}$ , έτσι ώστε για κάθε $n>n_{0}$ να ισχύει η σχέση $f(n)>cg(n)$ . $\Box$

Σχήμα 2.2: Γραφική αναπαράσταση του $\Omega$ .

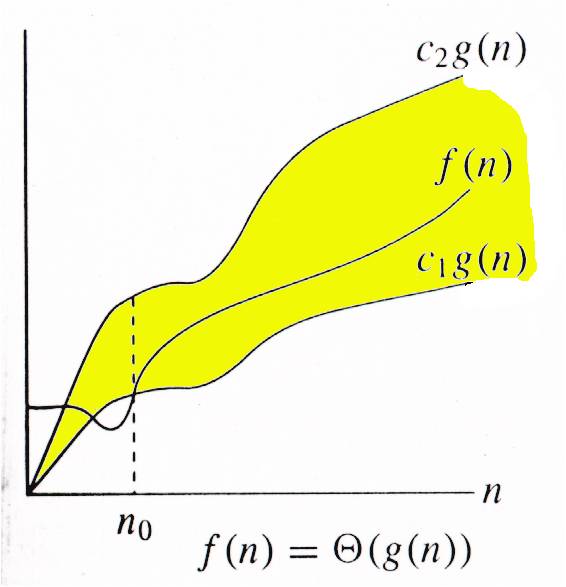
Συμβολισμός Θ.
Μία συνάρτηση $f(n)$ λέγεται ότι έχει πολυπλοκότητα της τάξης Θ( $g(n)$ ) και συμβολίζεται με $f(n)={\Theta}(g(n))$ ή με $f(n)\in{\Theta}(g(n))$ , αν υπάρχουν δύο θετικές σταθερές $c_{1},c_{2}$ και μία τιμή $n_{0}$ , έτσι ώστε κάθε για $n>n_{0}$ να ισχύει η σχέση $c_{2}g(n)<f(n)<c_{1}g(n)$ . $\Box$

Σχήμα 2.3: Γραφική αναπαράσταση του $\Theta$ .

Ας εξετάσουμε ένα απλό παράδειγμα, για να καταλάβουμε τη χρήση του συμβολισμού Θ. Έστω, λοιπόν, ότι πρέπει να αποδείξουμε τη σχέση:

\frac{n^{2}}{2}-\frac{n}{2}\ =\ {\Theta}(n^{2})

(2.46)

Ικανή και αναγκαία συνθήκη για να ισχύει η ανωτέρω σχέση, είναι να ισχύει η επόμενη:

c_{1}\ n^{2}\ \leq\ \frac{n^{2}}{2}-\frac{n}{2}\ \leq\ c_{2}\ n^{2}\Rightarrow

(2.47)

c_{1}\ \leq\ \frac{1}{2}-\frac{1}{2n}\ \leq\ c_{2}

(2.48)

όπου υπενθυμίζουμε ότι τα $c_{1},c_{2}$ πρέπει να είναι θετικοί πραγματικοί αριθμοί, ενώ το $n$ πρέπει να είναι θετικός ακέραιος. Εύκολα βλέπουμε ότι για $c_{2}=1/2$ και για $n\geq 1$ ισχύει το δεξιό σκέλος. Για το αριστερό σκέλος αρκεί να ισχύει $c_{1}=1/4$ και $n\geq 2$ . Συνεπώς, για $c_{1}=1/4,c_{2}=1/2$ και $n\geq 2$ ισχύει η ανωτέρω σχέση. Αποδείξεις που αφορούν στους άλλους δύο συμβολισμούς (Ο και Ω) μπορούν να διεκπεραιωθούν με αντίστοιχο τρόπο.

Με απλά λόγια, χρησιμοποιούμε το συμβολισμό Ο και το συμβολισμό Ω για να δηλώσουμε ότι η επίδοση ενός αλγορίθμου είναι ασυμπτωτικά φραγμένη από επάνω και από κάτω αντίστοιχα. Με το συμβολισμό Θ δηλώνουμε ότι η επίδοση ενός αλγορίθμου είναι ασυμπτωτικά φραγμένη από επάνω και από κάτω ταυτόχρονα. Οι συμβολισμοί Ο, Ω και Θ μπορεί να είναι περισσότερο ή λιγότερο περιοριστικοί ή σφικτοί (tight). Για παράδειγμα, είναι ευνόητο ότι ισχύει τόσο $2n^{2}={\rm O}(n^{2})$ όσο και $2n={\rm O}(n^{2})$ , όπου όμως η δεύτερη έκφραση είναι λιγότερη περιοριστική. Χρειαζόμαστε, λοιπόν, περισσότερο σφικτούς συμβολισμούς.

Συμβολισμός ο.
Μία συνάρτηση $f(n)$ λέγεται ότι έχει πολυπλοκότητα της τάξης ο( $g(n)$ ) και συμβολίζεται με $f(n)={\rm o}(g(n))$ ή με $f(n)\in{\rm o}(g(n))$ , αν για κάθε θετική σταθερά $c>0$ υπάρχει μία τιμή $n_{0}$ , έτσι ώστε για κάθε $n>n_{0}$ να ισχύει η σχέση $f(n)<cg(n)$ . $\Box$

Συμβολισμός ο. (εναλλακτικά)
Μία συνάρτηση $f(n)$ λέγεται ότι έχει πολυπλοκότητα της τάξης ο( $g(n)$ ) και συμβολίζεται με $f(n)={\rm o}(g(n))$ , αν ισχύει: $\lim_{n\rightarrow\infty}\frac{f(n)}{g(n)}=0$ . $\Box$

Συμβολισμός ω.
Μία συνάρτηση $f(n)$ λέγεται ότι έχει πολυπλοκότητα της τάξης ω( $g(n)$ ) και συμβολίζεται με $f(n)={\omega}(g(n))$ ή με $f(n)\in{\omega}(g(n))$ , αν για κάθε θετική σταθερά $c>0$ υπάρχει μία τιμή $n_{0}$ , έτσι ώστε για κάθε $n>n_{0}$ να ισχύει η σχέση $f(n)>cg(n)$ . $\Box$

Συμβολισμός ω. (εναλλακτικά)
Μία συνάρτηση $f(n)$ λέγεται ότι έχει πολυπλοκότητα της τάξης ω( $g(n)$ ) και συμβολίζεται με $f(n)={\omega}(g(n))$ , αν ισχύει: $\lim_{n\rightarrow\infty}\frac{f(n)}{g(n)}=\infty$ . $\Box$

Κοινός τόπος σε όλους τους συμβολισμούς, λοιπόν, είναι η λέξη «ασυμπτωτικά». Η έννοια αυτή είναι δάνειο από τα καθαρά μαθηματικά (θεωρία αριθμών) και εμπεδώθηκε στην Πληροφορική από τον Knuth. Για τους συμβολισμούς αυτούς ισχύουν πολλές από τις ιδιότητες των πραγματικών αριθμών. $\Box$

Μεταβατική ιδιότητα. (transitivity)
$f(n)$ =Ο $(g(n))$ και $g(n)$ =O $(h(n))$ $\Rightarrow$ $f(n)$ =Ο $(h(n))$
$f(n)$ =Ω $(g(n))$ και $g(n)$ =Ω $(h(n))$ $\Rightarrow$ $f(n)$ =Ω $(h(n))$
$f(n)$ =Θ $(g(n))$ και $g(n)$ =Θ $(h(n))$ $\Rightarrow$ $f(n)$ =Θ $(h(n))$
$f(n)$ =ο $(g(n))$ και $g(n)$ =ο $(h(n))$ $\Rightarrow$ $f(n)$ =ο $(h(n))$
$f(n)$ =ω $(g(n))$ και $g(n)$ =ω $(h(n))$ $\Rightarrow$ $f(n)$ =ω $(h(n))$

Ανακλαστική ιδιότητα. (reflexivity)
$f(n)$ = Ο $(f(n))$
$f(n)$ = Ω $(f(n))$
$f(n)$ = Θ $(f(n))$

Συμμετρική ιδιότητα. (symmetry)
$f(n)$ = Θ $(g(n))$ αν και μόνο αν $g(n)$ = Θ $(f(n))$

Ανάστροφη Συμμετρική ιδιότητα. (transpose symmetry)
$f(n)$ = Ο $(g(n))$ αν και μόνο αν $g(n)$ = Ω $(f(n))$
$f(n)$ = ο $(g(n))$ αν και μόνο αν $g(n)$ = ω $(f(n))$

Για μία καλύτερη κατανόηση των πέντε αυτών συμβολισμών, παρουσιάζουμε τον Πίνακα 2.1. Στο αριστερό σκέλος μέσω του αντίστοιχου συμβολισμού δίνεται η σχέση μεταξύ των συναρτήσεων $f(n)$ και $g(n)$ , ενώ στο δεξιό σκέλος δίνεται η σχέση μεταξύ των πραγματικών αριθμών $a$ και $b$ . Διδακτική αξία έχει η κατανόηση της αναλογίας μεταξύ των πέντε συμβολισμών με τις πέντε σχέσεις διάταξης. Σημειώνεται, όμως, ότι αν και δύο πραγματικοί αριθμοί είναι πάντοτε συγκρίσιμοι, εντούτοις δεν συμβαίνει το ίδιο πάντοτε για δύο ασυμπτωτικές εκφράσεις. Για παράδειγμα, δεν είναι δυνατόν οι συναρτήσεις $f(n)=n$ και $g(n)=n^{1+\cos n}$ να συσχετισθούν με κάποιο συμβολισμό.

$f(n)$ =Ο $(g(n))$	$a\leq b$
$f(n)$ =Ω $(g(n))$	$a\geq b$
$f(n)$ =Θ $(g(n))$	$a=b$
$f(n)$ =ο $(g(n))$	$a<b$
$f(n)$ =ω $(g(n))$	$a>b$

Πίνακας 2.1: Συσχέτιση ασυμπτωτικών συμβολισμών.

Οι συμβολισμοί ο και θ, που χρησιμοποιούνται λιγότερα συχνά στη βιβλιογραφία, εκφράζουν επίσης την ασυμπτωτική συμπεριφορά αλγορίθμων. Ωστόσο, σε αντίθεση με τους συμβολισμούς Ο, Ω και Θ, οι συμβολισμοί ο και ω χρησιμοποιούνται για να εκφράσουν λιγότερο περιοριστικές καταστάσεις ασυμπτωτικά. Έτσι, ισχύει $2n={\rm o}(n^{2})$ , αλλά $2n^{2}\neq{\rm o}(n^{2})$ .

Ας εξετάσουμε ένα ακόμη απλό παράδειγμα σε σχέση με το συμβολισμό ο. Έστω, λοιπόν, ότι για $a$ θετικό ακέραιο πρέπει να αποδείξουμε τη σχέση:

n^{a}\ \in\ {\rm o}(2^{n})

(2.49)

Λαμβάνουμε το όριο το λόγου των δύο συναρτήσεων και εφαρμόζουμε τον κανόνα του L’Hopital διαδοχικά:

\lim_{n\rightarrow\infty}\frac{n^{a}}{2^{n}}\ =\ \lim_{n\rightarrow\infty}% \frac{n^{a}}{e^{n\ln 2}}\ =\ \lim_{n\rightarrow\infty}\frac{an^{a-1}}{\ln 2\ e% ^{n\ln 2}}\ =\ \ldots\ =\ \lim_{n\rightarrow\infty}\frac{a!}{(\ln 2)^{a}\ e^{n% \ln 2}}\ =\ 0

(2.50)

Για να γίνουν συγκριτικά αντιληπτοί οι προηγούμενοι συμβολισμοί, ας θεωρήσουμε τη σχέση $f(n)=4n^{3}+3$ . Στην περίπτωση αυτή ισχύει:
$f(n)={\Theta}(n^{3})$
$f(n)={\rm O}(n^{3})={\rm O}(n^{4})\ldots$
$f(n)={\Omega}(n^{3})={\Omega}(n^{2}))={\Omega}(n)={\Omega}(1)$
$f(n)={\rm o}(n^{4})={\rm o}(n^{5})\ldots$
$f(n)={\omega}(n^{2})={\omega}(n)={\omega}(1)$

Συνδέοντας με το υλικό του προηγουμένου καφαλαίου, λοιπόν, σκοπός μας είναι αρχικά η εύρεση του χρονικού κόστους ενός αλγορίθμου με τη βοήθεια μίας συνάρτησης $f(n)$ , ενώ στη συνέχεια πρέπει να βρούμε κάποια συνάρτηση $g(n)$ με τον αντίστοιχο συμβολισμό. Αυτό που γίνεται συχνότερα στην πράξη, όπου προκύπτουν εκθετικές ή πολυωνυμικές συναρτήσεις, είναι να απομονώσουμε τον όρο με το μεγαλύτερο ειδικό βάρος αγνοώντας τους άλλους όρους καθώς και τους σταθερούς συντελεστές.

2.3 Χρήση Συμβολισμών στην Ανάλυση

Ας θυμηθούμε από τα Κεφάλαια 1.4-1.5 τις εκφράσεις που έχουν προκύψει σχετικά με την επίδοση των αλγορίθμων ταξινόμησης με επιλογή και με εισαγωγή. Πιο συγκεκριμένα, κατά την επακριβή ανάλυση για την ταξινόμηση με επιλογή είχαμε καταλήξει στις εκφράσεις:

	$\displaystyle T(n)$	$\displaystyle=$	$\displaystyle(c_{3}/2+c_{4}/2)n^{2}+(c_{1}+c_{2}+c_{3}/2-c_{4}/2+c_{5}+c_{6}+c% _{7})n+c_{1}$
		$\displaystyle=$	$\displaystyle an^{2}+bn+c$

Επίσης, είχαμε διαπιστώσει ότι η ταξινόμηση με επιλογή έχει την ίδια επίδοση για την καλύτερη, τη μέση και τη χειρότερη περίπτωση ανεξαρτήτως των δεδομένων εισόδου και συνεπώς ο αλγόριθμος αυτός θεωρείται σταθερός (robust). Για το συγκεκριμένο αλγόριθμο και τη συγκεκριμένη ανάλυση εύκολα συμπεραίνεται ότι $T(n)=g(\rm O(n^{2}))$ , αλλά και $T(n)=g(\Omega(n^{2}))$ και τελικά προκύπτει $T(n)=g(\Theta(n^{2}))$ . Έτσι, τελικά καταλήγουμε σε μία τυπική έκφραση (δηλαδή το $\Theta(n^{2})$ ), για να δηλώσουμε με συμπυκνωμένο τρόπο την πολυπλοκότητα του αλγορίθμου.

Τώρα θα εξετάσουμε με περισσότερη λεπτομέρεια και πάλι την ταξινόμηση με εισαγωγή. Όπως έχουμε αναφέρει προηγουμένως, για μία ολόκληρη κατηγορία αλγορίθμων ταξινόμησης, ως βαρόμετρο επιλέγεται η πράξη της σύγκρισης. Στη συγκεκριμένη περίπτωση, ως βαρόμετρο επιλέγεται η σύγκριση A[i]>key στην εντολή 4 (αγνοώντας τις εσωτερικές συγκρίσεις της εντολής του βρόχου for στην εντολή 1, καθώς και τη σύγκριση i>0 στην εντολή 4). Εύκολα προκύπτει ότι στη χειρότερη περίπτωση, για συγκεκριμένο i, το key είναι μικρότερο από κάθε A[i], όπου το i κυμαίνεται από 1 μέχρι n-1, οπότε το key θα συγκριθεί διαδοχικά με τα A[i-1], A[i-2], ..., A[1] πριν εξέλθουμε από το βρόχο, επειδή ισχύει η συνθήκη i=0. Από αυτή τη βασική σκέψη συνεπάγεται ότι καθώς το j μεταβάλλεται από 2 μέχρι n, στη χειρότερη περίπτωση ο συνολικός αριθμός των συγκρίσεων είναι:

\sum_{j=2}^{n}(j-1)\ =\ n(n-1)/2\ =\ {\Theta}(n^{2})

(2.51)

Στη συνέχεια θα εξετάσουμε λεπτομερέστερα τη μέση περίπτωση. Ας υποθέσουμε ότι τα στοιχεία του πίνακα είναι διακριτά (δηλαδή διαφορετικά μεταξύ τους) και ότι είναι ισοπίθανο να εμφανισθεί μία οποιαδήποτε διάταξη των $n$ στοιχείων. Άρα, όταν θεωρούμε την τιμή key=A[j] (εντολή 2), που πρέπει να παρεμβληθεί μεταξύ στοιχείων A[1], A[2], ..., A[j-1], δεχόμαστε ότι το key μπορεί με ίδια πιθανότητα να είναι το $k$ -οστό μεγαλύτερο, για $1\leq k\leq j$ . Αν, λοιπόν, το key είναι το μεγαλύτερο, αυτό θα γίνει αντιληπτό με μία σύγκριση με το στοιχείο A[j-1], αν είναι το δεύτερο μεγαλύτερο, αυτό θα γίνει αντιληπτό με δύο συγκρίσεις, κοκ, αν είναι το ( $j-1$ )-οστό μεγαλύτερο, αυτό θα γίνει αντιληπτό με $j-1$ συγκρίσεις, ενώ τέλος, αν είναι το $j$ -οστό μεγαλύτερο (δηλαδή το μικρότερο), αυτό θα γίνει αντιληπτό και πάλι με $j-1$ συγκρίσεις. Συνεπώς, η μέση τιμή των συγκρίσεων για μία δεδομένη τιμή του $j$ είναι:

	$\displaystyle c_{j}$	$\displaystyle=$	$\displaystyle\frac{1}{j}\left(1+2+3+\ldots+(j-1)+(j-1)\right)$
		$\displaystyle=$	$\displaystyle\frac{1}{j}\left(\sum_{i=1}^{j}i-1\right)\ =\ \frac{j+1}{2}-\frac% {1}{j}$

Θεωρώντας ότι το $j$ μεταβάλλεται από 2 μέχρι $n$ , έχουμε:

\sum_{j=2}^{n}c_{j}\ =\ \sum_{j=2}^{n}\left(\frac{j+1}{2}-\frac{1}{j}\right)\ % =\ \frac{n^{2}+3n}{4}-H_{n}\ =\ {\Theta}(n^{2})

(2.52)

Στο τελευταίο στάδιο της ανωτέρω σχέσης ισχύει ότι $H_{n}={\Theta}(\lg n)$ και επομένως αγνοείται ως προς το $n^{2}/4$ . Τελικά, λοιπόν, προκύπτει και τυπικά ότι τόσο στη χειρότερη περίπτωση, όσο και στη μέση περίπτωση η πολυπλοκότητα της ταξινόμησης με εισαγωγή είναι ${\Theta}(n^{2})$ . Ωστόσο, εύκολα διαπιστώνεται ότι στην καλύτερη περίπτωση ισχύει Θ $(n)$ .

2.4 Χειρισμός Αθροισμάτων

Επαγωγή

Τη μέθοδο αυτή γνωρίζουμε από το μάθημα των Διακριτών Μαθηματικών, αλλά εδώ απλώς θα αναπτύξουμε ένα παράδειγμα ως μία εναλλακτική απόδειξη σε σχέση με την ανάλυση των παλίνδρομων που αναφέραμε στο Κεφάλαιο 1.6. Με λίγα λόγια, δοθείσης μίας σχέσης προς απόδειξη, κατά την επαγωγή αποδεικνύουμε ότι η σχέση ισχύει για μικρά $n$ , υποθέτουμε ότι ισχύει για τυχόν $k$ και τέλος αποδεικνύουμε ότι ισχύει για $k+1$ .

Για παράδειγμα, θα αποδείξουμε επαγωγικά ότι για άρτια $n$ ισχύει:

\sum_{i=0}^{n/2-1}\ \frac{i}{2^{i+1}}\ =\ 1-\frac{n/2+1}{2^{n/2}}

(2.53)

Εύκολα φαίνεται ότι για $n=2$ , τότε αριστερό και δεξιό μέλος ισούνται με 0. Δεχόμαστε ότι ισχύει η σχέση για τυχόν άρτιο $k$ :

\sum_{i=0}^{k/2-1}\ \frac{i}{2^{i+1}}\ =\ 1-\frac{k/2+1}{2^{k/2}}

(2.54)

και θα αποδείξουμε ότι ισχύει για $k+2$ :

\sum_{i=0}^{k/2}\ \frac{i}{2^{i+1}}\ =\ 1-\frac{k/2+2}{2^{k/2+1}}

(2.55)

Λαμβάνουμε το αριστερό σκέλος και διαδοχικά έχουμε:

	$\displaystyle\sum_{i=0}^{k/2}\ \frac{i}{2^{i+1}}$	$\displaystyle=$	$\displaystyle\sum_{i=0}^{k/2-1}\ \frac{i}{2^{i+1}}+\frac{k/2}{2^{k/2+1}}\ =\ 1% -\frac{k/2+1}{2^{k/2}}+\frac{k/2}{2^{k/2+1}}$
		$\displaystyle=$	$\displaystyle 1-\frac{k+2}{2^{k/2+1}}+\frac{k/2}{2^{k/2+1}}\ =\ 1-\frac{k/2+2}% {2^{k/2+1}}$

Περιορισμός όρων

Δεδομένου ενός αθροίσματος, αντικαθιστούμε κάθε όρο του αθροίσματος με μία μεγαλύτερη ποσότητα που μπορούμε ευκολότερα να χειρισθούμε. Επί παραδείγματι, αν θεωρήσουμε ως γενικό πρότυπο τη σχέση $\sum_{i=1}^{n}a_{i}\ \leq\ na_{max}$ , τότε για το γνωστό μας άθροισμα μπορεί εναλλακτικά να προκύψει:

\sum_{i=1}^{n}i\ \leq\ \sum_{i=1}^{n}n\ =\ n^{2}\ =\ {\rm O}(n^{2})

(2.56)

Δεδομένου ενός αθροίσματος $\sum_{i=0}^{n}a_{i}$ , ας υποθέσουμε ότι $a_{k+1}/a_{k}\leq r$ , όπου $k\geq 0$ , ενώ ισχύει για τη σταθερά $r<1$ . Έτσι, λοιπόν, ισχύει:

\sum_{i=0}^{n}a_{i}\ \leq\ \sum_{i=0}^{\infty}a_{0}r^{i}\ =\ a_{0}\sum_{i=0}^{% \infty}r^{i}\ =\ a_{o}\frac{1}{1-r}

(2.57)

Θα προσεγγίσουμε το άθροισμα $\sum_{i=1}^{\infty}(i/3^{i})$ με βάση τη μέθοδο αυτή και λαμβάνουμε το λόγο:

\frac{a_{k+1}}{a_{k}}\ =\ \frac{(i+1)/3^{i+1}}{i/3^{i}}\ =\ \frac{i+1}{3i}\ % \leq\ \frac{2}{3}

(2.58)

Δηλαδή, για κάθε $k\geq 1$ ισχύει $r=2/3$ , οπότε:

\sum_{i=1}^{\infty}(i/3^{i})\ \leq\ \sum_{i=1}^{\infty}\frac{1}{3}\ \large(% \frac{2}{3}\large)^{i}\ =\ \frac{1}{3}\ \frac{1}{1-2/3}\ =\ 1

(2.59)

Διάσπαση αθροισμάτων

Δεδομένου ενός αθροίσματος, το επιμερίζουμε σε μικρότερα που μπορούν να επιλυθούν ευκολότερα. Επί παραδείγματι, για το γνωστό άθροισμα ισχύει:

	$\displaystyle\sum_{i=1}^{n}i$	$\displaystyle=$	$\displaystyle\sum_{i=1}^{n/2}i+\sum_{i=n/2+1}^{n}i$
		$\displaystyle\geq$	$\displaystyle\sum_{i=1}^{n/2}0+\sum_{i=n/2+1}^{n}(n/2)\ \geq\ (n/2)^{2}\ =\ {% \Omega}(n^{2})$

Τώρα θα χρησιμοποιήσουμε την παρούσα τεχνική μαζί με την προηγούμενη τεχνική (περιορισμός όρων) για το άθροισμα $\sum_{i=0}^{\infty}i^{2}/2^{i}$ . Λαμβάνοντας το λόγο δύο διαδοχικών όρων έχουμε:

\frac{a_{k+1}}{a_{k}}\ =\ \frac{(i+1)^{2}/2^{i+1}}{i^{2}/2^{i}}\ =\ \frac{(i+1% )^{2}}{2i^{2}}\ \leq\ \frac{8}{9}

(2.60)

για κάθε $k\geq 3$ . Επομένως, θα επιμερίσουμε αναλόγως το άθροισμα:

	$\displaystyle\sum_{i=0}^{\infty}i^{2}/2^{i}$	$\displaystyle=$	$\displaystyle\sum_{i=0}^{2}i^{2}/2^{i}+\sum_{i=3}^{\infty}i^{2}/2^{i}$
		$\displaystyle=$	$\displaystyle{\rm O}(1)+\frac{9}{8}\sum_{i=3}^{\infty}\left(\frac{8}{9}\right)% ^{i}\ =\ {\rm O}(1)$

καθώς το δεύτερο άθροισμα είναι φθίνουσα γεωμετρική πρόοδος.

Χρήση ολοκληρωμάτων

Ένα άθροισμα με μία αύξουσα συνάρτηση $f(k)$ μπορεί να περιορισθεί από ολοκληρώματα με βάση το γενικό τύπο:

\int_{m-1}^{n}f(x)dx\leq\sum_{m}^{n}f(k)\leq\int_{m}^{n+1}f(x)dx

(2.61)

θεωρώντας ότι σε μία γραφική παράσταση η καμπύλη της συνάρτησης $f(k)$ προσεγγίζεται από επάνω και κάτω από μεγαλύτερα και μικρότερα ορθογώνια. Αντίστοιχα, μία φθίνουσα συνάρτηση $f(k)$ μπορεί να περιορισθεί με βάση το γενικό τύπο:

\int_{m}^{n+1}f(x)dx\leq\sum_{m}^{n}f(k)\leq\int_{m-1}^{n}f(x)dx

(2.62)

Για τον αρμονικό αριθμό $H_{n}$ ισχύει:

\sum_{i=1}^{n}\frac{1}{i}\ \geq\ \int_{1}^{n+1}\frac{dx}{x}\ =\ \ln(n+1)

(2.63)

και

\sum_{i=2}^{n}\frac{1}{i}\ \leq\ \int_{1}^{n}\frac{dx}{x}\ =\ \ln n\Rightarrow% \sum_{i=1}^{n}\frac{1}{i}\ \leq\ \ln n+1

(2.64)

Επομένως, σε περιπτώσεις εύρεσης της πολυπλοκότητας αρκεί η χρήση της σχέσης $H_{n}={\Theta}(\lg n)$ .

2.5 Κατηγοριοποίηση Αλγορίθμων

Αφού λοιπόν ορίσθηκαν και τυπικά οι συμβολισμοί της πολυπλοκότητας, είναι δυνατόν να κατηγοριοποιήσουμε τους διαφόρους αλγορίθμους σε μία από τις επόμενες κατηγορίες:

: Ο(1). Κάθε εντολή εκτελείται σε πεπερασμένο πλήθος φορές, οπότε λέγεται ότι ο αλγόριθμος είναι «σταθερής πολυπλοκότητας». Συνήθως αναφέρεται σε πράξεις εύρεσης ενός στοιχείου ή ενημέρωσης ενός συνόλου στοιχείων.
: Ο( $\log n$ ). Ο αλγόριθμος είναι «λογαριθμικής πολυπλοκότητας». Με « $\log$ » και με « $\ln$ » θα συμβολίζεται ο δυαδικός και ο φυσικός λογάριθμος, αντιστοίχως. Πρακτικά, οι λογάριθμοι που θα χρησιμοποιηθούν είναι κυρίως δυαδικοί. Συνήθως αναφέρεται σε πράξεις εύρεσης ενός στοιχείου ή ενημέρωσης ενός συνόλου στοιχείων.
: O( $n$ ). Η πολυπλοκότητα λέγεται «γραμμική». Γενικώς, αυτή είναι η επίδοση ενός αλγορίθμου που πρέπει να εξετάσει ή να δώσει στην έξοδο $n$ στοιχεία.
: O( $n\log n$ ). Διαβάζεται όπως ακριβώς γράφεται (δηλαδή «n log n») χωρίς να χρησιμοποιείται κάποιο επίθετο (π.χ. γραμμολογαριθμική). Στην κατηγορία αυτή ανήκουν πολλοί αλγόριθμοι ταξινόμησης.
: O( $n^{2}$ ). Αναφέρεται ως «τετραγωνική πολυπλοκότητα». Ο δυναμικός προγραμματισμός για απλά προβλήματα, όπως αντιστοίχηση ακολουθιών.
: O( $n^{3}$ ). Αναφέρεται ως «κυβική πολυπλοκότητα». Οι αλγόριθμοι αυτοί πρέπει να χρησιμοποιούνται μόνο για προβλήματα μικρού μεγέθους. Χαρακτηριστικό παράδειγμα είναι ο γραμμικός προγραμματισμός.
: O( $2^{n}$ ). Σπάνια στην πράξη χρησιμοποιούνται αλγόριθμοι «εκθετικής πολυπλοκότητας», ενώ πάρα πολλά γνωστά προβλήματα έχουν αυτή την επίδοση. Ένα από τα πιο γνωστά είναι το πρόβλημα του περιοδεύοντος πωλητή.

Πολυπλοκότητα	$n=20$	$n=40$	$n=60$
O( $n$ )	0.00002 sec	0.00004 sec	0.00006 sec
O( $n^{2}$ )	0.0004 sec	0.0016 sec	0.0036 sec
O( $n^{3}$ )	0.008 sec	0.064 sec	0.216 sec
O( $2^{n}$ )	1 sec	12.7 ημέρες	366 αιώνες
O( $n!$ )	771 αιώνες	$3\cdot 10^{32}$ αιώνες	$3\cdot 10^{66}$ αιώνες

Πίνακας 2.2: Σύγκριση πολυπλοκότητας αλγορίθμων

Στον Πίνακα 2.2 υπολογίζεται ο χρόνος που απαιτείται από αλγορίθμους διαφόρων πολυωνυμικών και εκθετικών πολυπλοκοτήτων ως συνάρτηση του μεγέθους του προβλήματος. Για να γίνουν οι χρονικές εκτιμήσεις υποτίθεται ότι κάθε στοιχειώδης πράξη απαιτεί ένα msec στη CPU. Έτσι, αν για έναν αλγόριθμο τάξης Ο( $n^{3}$ ) διπλασιασθεί το μέγεθος του προβλήματος, τότε απαιτείται οκταπλάσιος ( $2^{3}$ ) χρόνος για να περατωθεί ο αλγόριθμος. Διαπιστώνεται αμέσως ότι οι αλγόριθμοι εκθετικής πολυπλοκότητας δεν είναι πρακτικής χρησιμότητας ακόμη και για μικρό αριθμό δεδομένων.

Επειδή η βελτίωση των αλγορίθμων είναι ζωτικής σημασίας, μία ιδιαίτερη περιοχή της Πληροφορικής, η Υπολογιστική Πολυπλοκότητα (Computational Complexity), διερευνά από θεωρητική και αναλυτική άποψη τους αλγορίθμους και τους ταξινομεί αναλόγως με την επίδοσή τους. Συνεχώς αναπτύσσονται νέοι καλύτεροι αλγόριθμοι, ενώ άλλοι περιθωριοποιούνται ως μη αποτελεσματικοί. Ένας αλγόριθμος λέγεται βέλτιστος (optimal), αν αποδειχθεί ότι δεν μπορεί να κατασκευασθεί καλύτερος.

Αιτιοκρατικοί (deterministic) λέγονται οι αλγόριθμοι των οποίων τα βήματα εκτέλεσης είναι σε κάθε χρονική στιγμή καθορισμένα και μοναδικά. Πιθανοτικοί-στοχαστικοί λέγονται οι αλγόριθμοι των οποίων τα βήματα εκτέλεσης εξαρτώνται από τυχαίες επιλογές που γίνονται κατά την διάρκεια εκτέλεσής του. Η έννοια του ανταιτιοκρατικού (non-deterministic) αλγορίθμου είναι μία θεωρητική έννοια και παραπέμπει σε υπολογιστικές μηχανές που έχουν την δυνατότητα τεράστιου παραλληλισμού. Διαισθητικά, επιτρέπεται η κλωνοποίηση της μηχανής, ώστε αυτή να εκτελεί μία συγκεκριμένη περίπτωση υπολογισμού.

Πολυωνυμικοί (polynomial) λέγονται οι αιτιοκρατικοί αλγόριθμοι με πολυπλοκότητα που φράσσεται άνω από μία πολυωνυμική έκφραση. Για παράδειγμα, πολυωνυμικοί είναι οι αλγόριθμοι τάξης Ο( $n$ ), O( $n^{3/2}$ ), O( $n^{2}$ ) κ.τ.λ. Συνήθως δεν απαιτούν μεγάλη υπολογιστική προσπάθεια σε αντίθεση με τους αλγορίθμους πολυπλοκότητας τάξης O( $n!$ ), O( $2^{n}$ ) ή O( $n^{n}$ ), που ονομάζονται μη πολυωνυμικοί.

Το σύνολο των προβλημάτων που μπορούν να επιλυθούν από αιτιοκρατικούς αλγορίθμους σε πολυωνυμικό χρόνο αποτελεί το σύνολο $P$ , ενώ το σύνολο των προβλημάτων που μπορούν να επιλυθούν από μη αιτιοκρατικούς αλγορίθμους σε χρόνο πολυωνυμικό αποτελεί το σύνολο $Ν Ρ$ , που σημαίνει μη αιτιοκρατικά πολυωνυμικά (nondeterministic polynomial) προβλήματα. Ένας εναλλακτικός ορισμός για το σύνολο προβλημάτων $N P$ αφορά όλα τα προβλήματα των οποίων μία υποψήφια λύση μπορεί να ελεγχθεί σε πολυωνυμικό χρόνο. Προφανώς το σύνολο $Ρ$ είναι υποσύνολο του συνόλου $Ν Ρ$ , το αντίστροφο όμως φαίνεται ότι δεν ισχύει και αποτελεί ένα από τα σημαντικότερα θεωρητικά προβλήματα των Μαθηματικών και της Πληροφορικής.

Μεταξύ των προβλημάτων του συνόλου $Ν Ρ$ διακρίνεται η σημαντική κατηγορία των $Ν Ρ$ -πλήρων ( $Ν Ρ$ -complete). Η επίλυση σε πολυωνυμικό χρόνο ενός προβλήματος που ανήκει σε αυτό το σύνολο συνεπάγεται την επίλυση σε πολυωνυμικό χρόνο όλων των $N P$ -πλήρων προβλημάτων.

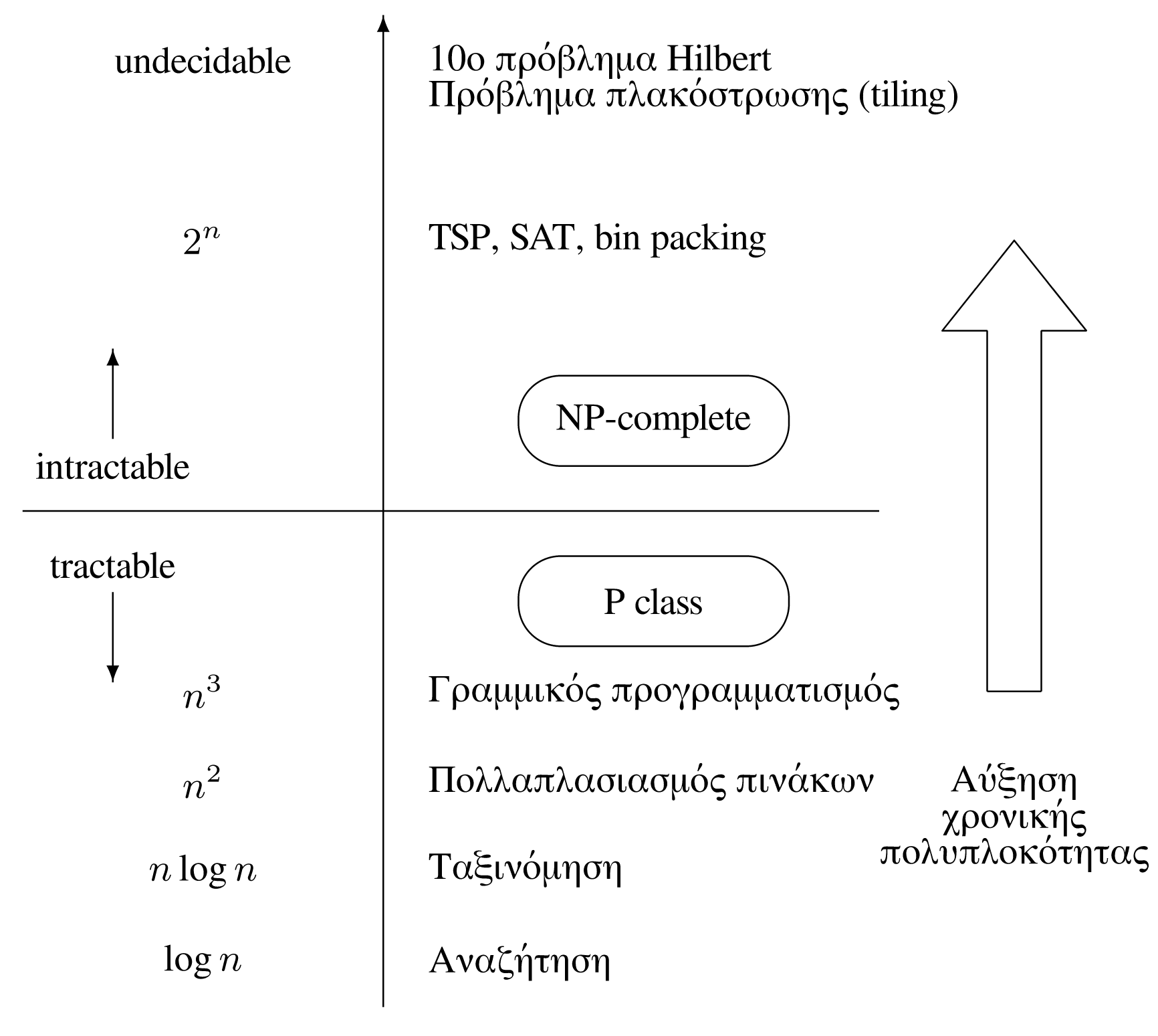
Σχήμα 2.4: Φάσμα υπολογιστικής πολυπλοκότητας

Το Σχήμα 2.4 απεικονίζει αυτό που αποκαλούμε «φάσμα της υπολογιστικής πολυπλοκότητας», δηλαδή ένα εξαιρετικά χονδρικό σχεδιάγραμμα των βασικών προβλημάτων μαζί με την πολυπλοκότητα των γρηγορότερων γνωστών αλγορίθμων που τα επιλύουν. Το σχήμα χωρίζεται σε δύο μεγάλες περιοχές προβλημάτων, τα δύσκολα ή δυσχείριστα (intractable) και τα εύκολα ή βατά (tractable). Στην κορυφή της πρώτης περιοχής ανήκουν τα προβλήματα για τα οποία δεν υπάρχουν σχετικοί αλγόριθμοι (undecidable). Πιο κάτω βρίσκονται τα προβλήματα για τα οποία υπάρχουν πρακτικά μη-χρήσιμοι αλγόριθμοι, διότι απαιτούν εκθετικό χρόνο. Μερικά τέτοια προβλήματα ανήκουν στο σύνολο $N P$ αλλά υπάρχουν και άλλα υπερσύνολα του $N P$ που δεν θα μας απασχολήσουν εδώ. Στη δεύτερη περιοχή βρίσκονται προβλήματα για τα οποία υπάρχουν γνωστοί, πρακτικά χρήσιμοι αλγόριθμοι. Είναι τα προβλήματα του είδους που εξετάζουμε σε αυτό το βιβλίο.

Ως προς το ανωτέρω σχήμα δίνονται οι επόμενες δύο επεξηγήσεις: Πρώτον, ο Hilbert ως 10ο πρόβλημα έθεσε το εξής: Δεδομένου ενός πολυωνύμου $Ρ$ με $n$ μεταβλητές και ακεραίους συντελεστές, να βρεθεί ένας αλγόριθμος που να προσδιορίζει αν η εξίσωση $Ρ=0$ έχει ή όχι ακέραιες λύσεις. Η απάντηση σε αυτό το πρόβλημα είναι αρνητική, όπως έδειξε ο Matiyasevich το 1970. Δεύτερον, η διατύπωση του προβλήματος SAT (satisfiability) έχει ως εξής: Έστω μία λογική έκφραση που αποτελείται από $n$ λογικές μεταβλητές και λογικοί τελεστές and, or, not. Υπάρχει συνδυασμός τιμών (δηλαδή αληθής/ψευδής) των μεταβλητών αυτών, έτσι ώστε η τελική τιμή της έκφρασης να είναι αληθής; Ο συνδυασμός όλων των δυνατών εισόδων που πρέπει να δοκιμασθούν είναι $2^{n}$ , άρα το πρόβλημα ανήκει στην κλάση ΝΡ. Μάλιστα το πρόβλημα SAT κατέχει κεντρική θέση στη θεωρία της πολυπλοκότητας, διότι τα περισσότερα NP-πλήρη προβλήματα προκύπτουν με πολυωνυμικές αναγωγές από αυτό. Επομένως, το πρόβλημα αυτό είναι και NP-πλήρες.

Η αδυναμία των ερευνητών να προτείνουν έναν πολυωνυμικό αλγόριθμο για πολλά δύσκολα προβλήματα επί του παρόντος δείχνει ότι δεν ισχύει η ισότητα Ρ=ΝΡ, αλλά ισχύει Ρ $\subseteq$ ΝΡ. H εικασία περί της ισότητας P=NP αποτελεί ένα από τα διασημότερα ανοικτά προβλήματα της σύγχρονης επιστήμης της Πληροφορικής και δεν αναμένεται να επιλυθεί εύκολα με τη χρήση των σημερινών συμβατικών υπολογιστικών μοντέλων. Η έρευνα ωστόσο παρακάμπτει το σημείο αυτό προχωρώντας στην ανάπτυξη προσεγγιστικών αλγορίθμων για την επίλυση των δύσκολων προβλημάτων, έτσι ώστε να επιτυγχάνεται μία αποδεκτή λύση σε πολυωνυμικό χρόνο. Περισσότερα στοιχεία σχετικά με τη θεωρητική πλευρά της ανάλυσης των αλγορίθμων είναι πέρα από τους σκοπούς αυτού του βιβλίου.

2.6 Εισαγωγή στις αναδρομικές εξισώσεις

Όπως κατά την μελέτη των ταξινομήσεων με εισαγωγή και επιλογή στο Κεφάλαιο 1 προέκυψαν εξισώσεις με την έκφραση $T(n)$ στο αριστερό σκέλος, συχνά κατά την ανάλυση αλγορίθμων προκύπτουν αντίστοιχες εξισώσεις, που όμως είναι αναδρομικές. Αυτό συμβαίνει όταν σχεδιάζεται ένας αλγόριθμος που σπάει το πρόβλημα σε μικρότερα υποπροβλήματα και εν συνεχεία εκτελεί αναδρομικά την ίδια ακολουθία βημάτων για κάθε υποπρόβλημα. Η επίλυση αναδρομικών εξισώσεων είναι ένα απαραίτητο εργαλείο για την εύρεση κλειστών εκφράσεων που περιγράφουν την πολυπλοκότητα πολλών αλλά και βασικών αλγορίθμων.

Ορισμός.
Για μία ακολουθία αριθμών $a_{0},a_{1},a_{2},\ldots,a_{n},\ldots$ μία εξίσωση που εκφράζει τον όρο $a_{n}$ με βάση τους προηγούμενους στην ακολουθία καλείται αναδρομική σχέση. Οι τιμές (ή τιμή) που πρέπει να γνωρίζουμε, ώστε να ξεκινήσει ο υπολογισμός ενός στοιχείου της ακολουθίας με βάση την αναδρομική σχέση καλούνται αρχικές συνθήκες. $\Box$

Σε προηγούμενη ενότητα του κεφαλαίου αναφέρθηκε η ακολουθία των αριθμών Fibonacci, 1,1,2,3,5,8, 13,21, κοκ, όπου οι δύο πρώτοι αριθμοί της ακολουθίας ισούνται με 1, ενώ κάθε επόμενος ισούται με το άθροισμα των δύο προηγουμένων. Η ακολουθία αυτή περιγράφεται εύκολα από την αναδρομική σχέση $a_{n}=a_{n-1}+a_{n-2}$ , για $n\geq 2$ με $a_{0}=1,a_{1}=1$ . Ωστόσο, είναι δύσκολο να βρεθεί μέσω της απλής παρατήρησης μία γενική έκφραση για το $a_{n}$ . Αυτό αποτελεί και το κύριο ενδιαφέρον, διότι αν το πλήθος των βημάτων ενός αλγορίθμου εκφρασθεί μέσω μίας αναδρομικής σχέσης, τότε μπορούμε να εκτιμήσουμε τη χρονική πολυπλοκότητα του προσδιορίζοντας τον γενικό όρο $a_{n}$ .

Αναδρομικές Σχέσεις	Παράδειγμα
Πρώτης Τάξης
$\circ$ γραμμικές	$a_{n}=na_{n-1}-1$
$\circ$ μη-γραμμικές	$a_{n}=\frac{1}{1+a_{n-1}}$
Δεύτερης Τάξης
$\circ$ γραμμικές	$a_{n}=a_{n-1}+2a_{n-2}$
$\circ$ μη-γραμμικές	$a_{n}=a_{n-1}a_{n-2}+2\sqrt{a_{n-2}}$
$\circ$ γραμμικές με μεταβλητούς συντελεστές	$a_{n}=na_{n-1}+(n-1)a_{n-2}+1$
$k$ Τάξης	$a_{n}=F(a_{n-1},a_{n-2},\ldots,a_{n-k})$
Πλήρους Ιστορίας	$a_{n}=F(a_{n-1},a_{n-2},\ldots,a_{1})$
Διαίρει και Βασίλευε	$a_{n}=a_{\lceil n/2\rceil}+a_{\lfloor n/2\rfloor}+n$

Πίνακας 2.3: Κατηγοριοποίηση αναδρομικών εξισώσεων.

Στον Πίνακα 2.3 παρουσιάζεται η κατηγοριοποίηση των αναδρομικών σχέσεων αναλόγως με το πλήθος των απαραίτητων όρων για την έκφραση του $a_{n}$ και με τον τρόπο χρήσης αυτών των όρων. Στη συνέχεια, θα εξετάσουμε τρόπους προσδιορισμού ή φραγής του γενικού όρου $a_{n}$ μίας αναδρομικής σχέσης αναλόγως με την κλάση όπου ανήκει. Γενικώς, μία αναδρομική εξίσωση μπορεί να επιλυθεί με τις εξής μεθόδους:

•

με αντικατάσταση,
•

με επανάληψη,
•

με αναγωγή στη χαρακτηριστική εξίσωση,
•

με το γενικό θεώρημα και
•

με γεννήτριες συναρτήσεις.

Κατ’αρχάς, λοιπόν, θα εξετασθούν οι μέθοδοι της αντικατάστασης και της επανάληψης, στη συνέχεια μία σειρά τεχνικών αναγωγής στη χαρακτηριστική εξίσωση και τέλος η μέθοδος με βάση το γενικό θεώρημα. Η μέθοδος των γεννητριών συναρτήσεων θα παρουσιασθεί εκτενέστερα στο Κεφάλαιο 3.

2.7 Η Μέθοδος της Αντικατάστασης

Στη μέθοδο της αντικατάστασης γίνεται μία ασυμπτωτική εκτίμηση της λύσης, η οποία στην συνέχεια επαληθεύεται επαγωγικά.

Δίνεται η σχέση $a_{n}$ =2 $a_{n/2}$ + $n$ και εκτιμάται ότι η λύση είναι $a_{n}$ =O $(n\log n)$ . Για να είναι σωστή αυτή η εκτίμηση, θα πρέπει να ισχύει $a_{n}\leq cn\log n$ για κάποια σταθερά $c>0$ . Θα δείξουμε επαγωγικά ότι η πρόβλεψη αυτή είναι ορθή. Υποθέτουμε ότι για τιμές μικρότερες του $n$ η ανισότητα ισχύει, οπότε:

$\displaystyle a_{n}$	$\displaystyle=$	$\displaystyle 2a_{n/2}+n$
	$\displaystyle\leq$	$\displaystyle 2\ c\ \frac{n}{2}\log\frac{n}{2}+n$
	$\displaystyle=$	$\displaystyle c\ n\log\frac{n}{2}+n$
	$\displaystyle=$	$\displaystyle c\ n\log n-c\ n+n$
	$\displaystyle\leq$	$\displaystyle c\ n\log n$

κάτι που ισχύει για κάθε σταθερά $c\geq 1$ .

Ας εξετάσουμε ένα ακόμη παράδειγμα. Έστω η σχέση $a_{n}=a_{n-1}+n$ για $n>0$ και $a_{0}=0$ . Υποπτευόμαστε ότι ο γενικός όρος είναι της τάξης Ο( $n^{2}$ ), δηλαδή ότι ισχύει $a_{n}\leq cn^{2}$ για κάποια σταθερά $c>0$ και $n>n_{0}$ για κάποιο $n_{0}$ . Θα δείξουμε και πάλι επαγωγικά ότι η υποψία μας είναι ορθή. Υποθέτουμε ότι για τιμές μικρότερες του $n$ η ανισότητα ισχύει, οπότε:

$\displaystyle a_{n}$	$\displaystyle=$	$\displaystyle a_{n-1}+n$
	$\displaystyle\leq$	$\displaystyle c\ (n-1)^{2}+n$
	$\displaystyle=$	$\displaystyle c\ n^{2}+(1-2c)\ n+c$
	$\displaystyle\leq$	$\displaystyle c\ n^{2}$

όπου η τελευταία ανισοϊσότητα ισχύει, για παράδειγμα για $c=2$ και $n_{0}\geq 1$ .

2.8 Η Μέθοδος της Επανάληψης

Πολλές φορές αυτές οι αναδρομικές εξισώσεις επιλύονται με τη μέθοδο της επανάληψης. Η μέθοδος αυτή, όπως θα φανεί με τα επόμενα δύο παραδείγματα, ίσως είναι η απλούστερη (όταν μπορεί να εφαρμοσθεί), καθώς είναι αρκετά μηχανιστική.

Για παράδειγμα, δίνεται η αναδρομική εξίσωση:

T(n)\ =\ 4\ T(n/2)+n

(2.65)

όπου $n>1$ , ενώ η αρχική συνθήκη είναι $T(1)=1$ . Χωρίς βλάβη της γενικότητας, δεχόμαστε ότι ισχύει $n=2^{k}$ , οπότε $k=\log n$ . Αν στην προηγούμενη σχέση αντικαταστήσουμε την ποσότητα $T(n/2)$ , επαναλαμβάνοντας την εφαρμογή της αναδρομής με κατάλληλα μειωμένα τα ορίσματα, τότε προκύπτει:

	$\displaystyle T(n)$	$\displaystyle=$	$\displaystyle 4\ \left[4\ T(n/4)+n/2\right]+n$
		$\displaystyle=$	$\displaystyle 4^{2}\ T(n/2^{2})+2n+n$

Με μία-δύο ακόμη επαναλήψεις αντιλαμβανόμαστε το μηχανισμό παραγωγής των επόμενων σχέσεων με τις διαδοχικές αντικαταστάσεις των αναδρομών με μειωμένα ορίσματα. Άρα, ισχύει ότι:

T(n)\ =\ 4^{k}\ T(n/2^{k})+(2^{k-1}n+\ldots+2^{1}n+2^{0}n)

(2.66)

Λόγω της αρχικής συνθήκης ισχύει:

$\displaystyle T(n)$	$\displaystyle=$	$\displaystyle 4^{k}+(2^{k-1}n+\ldots+2^{1}n+2^{0}n)$
	$\displaystyle=$	$\displaystyle 4^{k}+n\ (1+2+\ldots+2^{k-1})$
	$\displaystyle=$	$\displaystyle 4^{k}+n\ \frac{2^{k}-1}{2-1}$
	$\displaystyle=$	$\displaystyle 4^{\log n}+n(n-1)$
	$\displaystyle=$	$\displaystyle 2n^{2}-n$

Έστω τώρα ένα δεύτερο παράδειγμα. Δίνεται η αναδρομική εξίσωση:

T(n)\ =\ 4\ T(n/2)+n^{2}/\log n

(2.67)

όπου και πάλι δεχόμαστε ότι $n=2^{k}$ και $T(1)=1$ . Με μία πρώτη επανάληψη προκύπτει ότι:

	$\displaystyle T(n)$	$\displaystyle=$	$\displaystyle 4^{2}\ T(n/2^{2})+n^{2}/\log n+n^{2}/\log(n/2)$
		$\displaystyle=$	$\displaystyle 4^{2}\ T(n/2^{2})+n^{2}\left(\frac{1}{\log n}+\frac{1}{\log n-1}\right)$

και με διαδοχικές επαναλήψεις βρίσκουμε ότι:

$\displaystyle T(n)$	$\displaystyle=$	$\displaystyle 4^{k}\ T(n/2^{k})+n^{2}\left(\frac{1}{\log n}+\frac{1}{\log n-1}% +\ldots+\frac{1}{\log n-(k-1)}\right)$
	$\displaystyle=$	$\displaystyle 4^{k}+n^{2}\ \left(\frac{1}{\log n}+\frac{1}{\log n-1}+\ldots+1\right)$
	$\displaystyle=$	$\displaystyle n^{2}+n^{2}\ H_{\log n}\ \approx\ n^{2}+n^{2}\ \log(\log n)$
	$\displaystyle=$	$\displaystyle{\Theta}(n^{2}\ \log(\log n))$

2.9 Ομογενείς Γραμμικές Αναδρομές

Η απλούστερη περίπτωση αναδρομικής εξίσωσης είναι της μορφής:

a_{0}t_{n}+a_{1}t_{n-1}+a_{2}t_{n-2}+\ldots a_{k}t_{n-k}\ =\ 0

(2.68)

και λέγεται γραμμική (linear) γιατί δεν περιέχει δυνάμεις και γινόμενα των $t_{i}$ , λέγεται ομογενής (homogeneous) γιατί ο γραμμικός συνδυασμός των $t_{i}$ ισούται με 0, ενώ επίσης έχει σταθερούς συντελεστές $a_{i}$ . Έστω ότι αναζητούμε μία λύση της μορφής:

t_{n}\ =\ x^{n}

(2.69)

όπου το $x$ είναι μία σταθερά. Αντικαθιστώντας στην αναδρομική εξίσωση έχουμε:

a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots a_{k}x^{n-k}\ =\ 0\Rightarrow

(2.70)

p(x)\ =\ a_{0}x^{k}+a_{1}x^{k-1}+a_{2}x^{k-2}+\ldots a_{k}\ =\ 0

(2.71)

που αποτελεί τη χαρακτηριστική εξίσωση της αναδρομής. Ας υποθέσουμε ότι η εξίσωση έχει $k$ διακριτές (πραγματικές) ρίζες $r_{1},r_{2},\ldots,r_{k}$ . Στην περίπτωση αυτή κάθε γραμμικός συνδυασμός:

t_{n}\ =\ \sum_{i=1}^{k}c_{i}r_{i}^{n}

(2.72)

είναι λύση της αναδρομής, όπου οι σταθερές $c_{i}$ εξαρτώνται από τις αρχικές συνθήκες.

Για παράδειγμα, έστω ότι δίνεται η αναδρομική εξίσωση:

t_{k}-5\ t_{k-1}+6\ t_{k-2}\ =\ 0

(2.73)

με αρχικές συνθήκες $t_{0}=3$ και $t_{1}=7$ . Η χαρακτηριστική εξίσωση είναι $x^{2}-5x+6=0$ με ρίζες $r_{1}=2$ και $r_{2}=3$ . Συνεπώς, καταλήγουμε ότι:

t_{k}\ =\ c_{0}\ 2^{k}+c_{1}\ 3^{k}

(2.74)

Επιλύοντας το σύστημα δύο εξισώσεων με δύο αγνώστους, που προκύπτει από τις αρχικές συνθήκες, έχουμε:

	$\displaystyle 3$	$\displaystyle=$	$\displaystyle c_{0}+c_{1}$
	$\displaystyle 7$	$\displaystyle=$	$\displaystyle 2\ c_{0}+3\ c_{1}$

από όπου προκύπτει ότι $c_{0}=2,c_{1}=1$ και, επομένως, η λύση της αναδρομής είναι $t_{k}=2^{k+1}+3^{k}$ .

Τώρα ας υποθέσουμε ότι οι λύσεις δεν είναι όλες διακριτές μεταξύ τους αλλά υπάρχει μία πολλαπλή ρίζα $r$ βαθμού $d$ . Επομένως, το πολυώνυμο $p(x)$ μπορεί να γραφεί ως εξής:

p(x)\ =\ (x-r)^{d}g(x)

(2.75)

όπου το $g(x)$ δεν έχει για ρίζα το $r$ , οπότε δεν διαιρείται με το $(x-r)$ . Παραγωγίζουμε και λαμβάνουμε:

p^{\prime}(x)\ =\ (x-r)^{d}g^{\prime}(x)+d(x-r)^{d-1}g(x)\ =\ (x-r)^{d-1}\left% ((x-r)g^{\prime}(x)+dg(x)\right)

(2.76)

όπου παρατηρούμε ότι το $p^{\prime}(x)$ έχει πολλαπλή ρίζα $r$ βαθμού $d-1$ . Το συμπέρασμα αυτό θα το χρησιμοποιήσουμε στη συνέχεια. Τώρα, εφόσον το πολυώνυμο $p(x)$ έχει πολλαπλή ρίζα $r$ βαθμού $d$ , έπεται ότι το $r$ είναι πολλαπλή ρίζα βαθμού $d$ και του πολυωνύμου:

x^{k-m}p(x)\ =\ a_{0}x^{k}+a_{1}x^{k-1}+\ldots+a_{m}x^{k-m}

(2.77)

Παραγωγίζουμε αυτή την έκφραση, πολλαπλασιάζουμε επί $x$ και λαμβάνουμε:

a_{0}kx^{k}+a_{1}(k-1)x^{k-1}+\ldots+a_{m}(k-m)x^{k-m}

(2.78)

Με βάση την ανωτέρω παρατήρηση, έπεται ότι η τελευταία έκφραση έχει πολλαπλή ρίζα $r$ βαθμού $d-1$ . Άρα, ισχύει:

a_{0}kr^{k}+a_{1}(k-1)r^{k-1}+\ldots+a_{m}(k-m)r^{k-m}\ =\ 0

(2.79)

Αν προσέξουμε καλύτερα αυτήν την αναδρομική εξίσωση, διαπιστώνουμε ότι έχει λύση $t_{k}=kr^{k}$ . Περαιτέρω, παραγωγίζοντας και πολλαπλασιάζοντας επί $x$ και πάλι προκύπτει η σχέση:

a_{0}k^{2}x^{k}+a_{1}(k-1)^{2}x^{k-1}+\ldots+a_{m}(k-m)^{2}x^{k-m}

(2.80)

με πολλαπλή ρίζα $r$ βαθμού $d-2$ . Επομένως, προκύπτει η αναδρομική εξίσωση:

a_{0}k^{2}r^{k}+a_{1}(k-1)^{2}r^{k-1}+\ldots+a_{m}(k-m)^{2}r^{k-m}\ =\ 0

(2.81)

με λύση $t_{k}=k^{2}r^{k}$ . Η διαδικασία αυτή μπορεί να συνεχισθεί για $d-1$ βήματα συνολικά. Έτσι, καταλήγουμε στο εξής συμπέρασμα: Αν ένα χαρακτηριστικό πολυώνυμο μίας ομογενούς γραμμικής αναδρομικής εξίσωσης έχει πολλαπλή ρίζα $r$ βαθμού $d$ , τότε οι λύσεις της εξίσωσης είναι $t_{k}=r^{k},kr^{k},k^{2}r^{k},\ldots,k^{d-1}r^{k}$ . Όπως και πριν, η γενική λύση της αναδρομικής εξίσωσης είναι γραμμικός συνδυασμός αυτών των λύσεων και πρέπει να ληφθούν υπ’όψιν οι αρχικές συνθήκες.

Για παράδειγμα, έστω ότι δίνεται η αναδρομική εξίσωση:

t_{k}-4\ t_{k-1}+4\ t_{k-2}\ =\ 0

(2.82)

με αρχικές συνθήκες $t_{0}=2$ και $t_{1}=10$ . Η χαρακτηριστική εξίσωση είναι $x^{2}-4x+4=(x-2)^{2}=0$ με διπλή ρίζα $r=2$ . Συνεπώς, καταλήγουμε ότι:

t_{k}\ =\ c_{0}\ 2^{k}+c_{1}\ k2^{k}

(2.83)

Επιλύοντας το σύστημα δύο εξισώσεων με δύο αγνώστους, που προκύπτει από τις αρχικές συνθήκες, έχουμε:

	$\displaystyle 2$	$\displaystyle=$	$\displaystyle c_{0}$
	$\displaystyle 10$	$\displaystyle=$	$\displaystyle 2\ c_{0}+2\ c_{1}$

από όπου προκύπτει ότι $c_{0}=2,c_{1}=3$ και, επομένως, η λύση της αναδρομής είναι $t_{k}=2^{k+1}+3\ k2^{k}$ .

2.10 Μη Ομογενείς Γραμμικές Αναδρομές

Ας θεωρήσουμε τώρα μη ομογενείς γραμμικές αναδρομικές εξισώσεις, δηλαδή εξισώσεις υπό την επόμενη μορφή, όπου ο γραμμικός συνδυασμός δεν ισούται με μηδέν:

a_{0}t_{n}+a_{1}t_{n-1}+a_{2}t_{n-2}+\ldots a_{k}t_{n-k}\ =\ b_{1}^{n}p_{1}(n)% +b_{2}^{n}p_{2}(n)+\ldots

(2.84)

ενώ τα $b_{1},b_{2},\ldots$ είναι σταθερές. Στο σημείο αυτό χωρίς απόδειξη δίνεται ότι ισοδύναμο είναι να θεωρηθεί η ομογενής γραμμική αναδρομική εξίσωση:

(a_{0}x^{k}+a_{1}x^{k-1}+a_{2}x^{k-2}+\ldots a_{k})(x-b_{1})^{d_{1}+1}(x-b_{2}% )^{d_{2}+1}\ldots\ =\ 0

(2.85)

όπου η πρώτη παρένθεση αποτελεί τη χαρακτηριστική εξίσωση του αριστερού σκέλους της μη ομογενούς αναδρομικής εξίσωσης, ενώ $d_{i}$ είναι ο βαθμός του πολυωνύμου $p_{i}(n)$ .

Για παράδειγμα, έστω ότι δίνεται η μη ομογενής αναδρομική εξίσωση:

t_{k}-2\ t_{k-1}\ =\ 2^{k}-1

(2.86)

με αρχική συνθήκη $t_{0}=0$ . Θεωρώντας ότι ισχύει: $b_{1}=2,b_{2}=1,p_{1}(n)=1$ και $p_{2}(n)=-1$ , η εξίσωση μετασχηματίζεται στην ομογενή:

(x-2)(x-1)(x-2)\ =\ 0

(2.87)

Έτσι, φθάνουμε σε μία ομογενή γραμμική αναδρομική εξίσωση με γενική λύση:

t_{k}\ =\ c_{0}\ 1^{κ}+c_{1}\ 2^{κ}+c_{2}\ k2^{k}

(2.88)

Πρέπει να επιλύσουμε ένα σύστημα τριών εξισώσεων με τρεις αγνώστους. Εύκολα υπολογίζουμε ότι $t_{1}=1,t_{2}=5$ :

$\displaystyle 0$	$\displaystyle=$	$\displaystyle c_{0}+c_{1}$
$\displaystyle 1$	$\displaystyle=$	$\displaystyle c_{0}+2\ c_{1}+2\ c_{2}$
$\displaystyle 5$	$\displaystyle=$	$\displaystyle c_{0}+4\ c_{1}+8\ c_{2}$

από όπου προκύπτει ότι $c_{0}=1,c_{1}=-1,c_{3}=1$ και, επομένως, η λύση της αναδρομής είναι $t_{k}=(k-1)\ 2^{k}+1$ .

Συνήθως οι μη ομογενείς αναδρομικές εξισώσεις μπορούν να επιλυθούν και με απλή άλγεβρα. Ας θεωρήσουμε και πάλι το προηγούμενο παράδειγμα με την εξίσωση $t_{k}-2\ t_{k-1}\ =\ 2^{k}-1$ . Πρώτον, πολλαπλασιάζουμε και τα δύο σκέλη της εξίσωσης επί δύο, οπότε προκύπτει:

2\ t_{k}-4\ t_{k-1}\ =\ 2^{k+1}-2

(2.89)

Δεύτερον, αντικαθιστούμε όπου $k$ με $k+1$ , οπότε προκύπτει:

t_{k+1}-2\ t_{k}\ =\ 2^{k+1}-1

(2.90)

Από τις δύο τελευταίες σχέσεις προκύπτει ότι:

t_{k+1}-4\ t_{k}+t_{k-1}\ =\ 1

(2.91)

Ούτε και αυτή η εξίσωση είναι ομογενής αλλά έχουμε κάνει ένα βήμα. Τρίτον, λοιπόν, στην τελευταία αυτή σχέση αντικαθιστούμε το $k$ με $k+1$ , οπότε προκύπτει:

t_{k+2}-4\ t_{κ+1}+t_{κ}\ =\ 1

(2.92)

Εξισώνοντας τα αριστερά σκέλη των δύο τελευταίων εξισώσεων προκύπτει η ομογενής εξίσωση:

t_{k+2}-5\ t_{k+1}+8\ t_{k}-4\ t_{k-1}\ =\ 0

(2.93)

που επιλύεται κατά τα γνωστά, καθώς έχει χαρακτηριστική εξίσωση:

x^{3}-5x^{2}+8x-4\ =\ (x-1)(x-2)^{2}\ =\ 0

(2.94)

2.11 Αλλαγή Μεταβλητής

Είναι δυνατόν κατά την ανάλυση αλγορίθμων να προκύψουν εξισώσεις με την έκφραση $T(n)$ στο αριστερό σκέλος, οι οποίες όμως δεν επιλύονται με τη μέθοδο της επανάληψης. Τότε αντικαθιστούμε το αριστερό σκέλος με την έκφραση $t_{n}$ με κάποια κατάλληλη αλλαγή της μεταβλητής (variable change), ώστε να προκύψει μία ομογενής ή μη ομογενής γραμμική αναδρομική εξίσωση, που να επιλύεται με βάση τη χαρακτηριστική εξίσωση.

Για παράδειγμα, έστω η απλή αναδρομική εξίσωση που επιλύθηκε με τη μέθοδο της επανάληψης στο Κεφάλαιο 2.8:

T(n)\ =\ 4\ T(n/2)+n

(2.95)

όπου το $n>1$ είναι δύναμη του 2. Έστω ότι ισχύει $n=2^{k}$ , οπότε $k=\log n$ . Έτσι, προκύπτει η σχέση:

T(2^{k})\ =\ 4\ T(2^{k-1})+2^{k}

(2.96)

που την ξαναγράφουμε με τη μορφή:

t_{k}\ =\ 4\ t_{k-1}+2^{k}

(2.97)

Για αυτή τη μη ομογενή αναδρομική εξίσωση μπορούμε εύκολα να βρούμε τη χαρακτηριστική εξίσωση:

(x-4)(x-2)\ =\ 0

(2.98)

οπότε η γενική λύση είναι της μορφής:

t_{k}\ =\ c_{1}\ 4^{k}+c_{2}\ 2^{k}

(2.99)

Επιστρέφοντας στην αρχική μεταβλητή, καταλήγουμε στην εξίσωση

T(n)\ =\ c_{1}\ n^{2}+c_{2}\ n

(2.100)

που επιλύεται, αν μας δοθούν οι αρχικές συνθήκες.

Προχωρούμε τώρα σε ένα συνθετότερο παράδειγμα που δεν μπορεί να επιλυθεί με τα μέχρι στιγμής γνωστά. Γενικώς, θα πρέπει να γίνονται μετασχηματισμοί, ώστε να αναγόμαστε στα γνωστά. Μία μέθοδος, λοιπόν, είναι να αλλάζουμε το εύρος της μεταβλητής (range transformation). Για παράδειγμα, έστω ότι δίνεται η αναδρομική εξίσωση:

T(n)\ =\ n\ T^{2}(n/2)

(2.101)

όπου το $n>1$ είναι δύναμη του 2, ενώ δίνεται και η αρχική συνθήκη $T(1)=6$ . Σύμφωνα με την προηγούμενη τεχνική (δηλαδή αλλαγή μεταβλητής θέτοντας $n=2^{k}$ ) καταλήγουμε στην ισοδύναμη έκφραση:

t_{k}\ =\ 2^{k}\ t_{k-1}^{2}

(2.102)

όπου $k>0$ , ενώ πλέον η αρχική συνθήκη είναι $t_{0}=6$ . Τώρα προχωρούμε σε μία αλλαγή μεταβλητής, όπου όμως ταυτόχρονα αλλάζουμε και το πεδίο ορισμού. Θέτουμε, λοιπόν, $V_{k}=\log t_{k}$ , οπότε προκύπτει:

V_{k}\ =\ k+2\ V_{k-1}

(2.103)

με αρχική συνθήκη $V_{0}=\log 6$ . Η τελευταία αναδρομική εξίσωση έχει χαρακτηριστική εξίσωση:

(x-2)(x-1)^{2}\ =\ 0

(2.104)

οπότε σύμφωνα με όσα αναπτύξαμε στην παράγραφο σχετικά με πολλαπλές ρίζες, προκύπτει η γενική λύση:

V_{k}\ =\ c_{1}\ 2^{k}+c_{2}\ 1^{k}+c_{3}\ k1^{k}

(2.105)

Από την αναδρομική εξίσωση ως προς $V_{k}$ βρίσκουμε τις αρχικές συνθήκες:

$\displaystyle V_{0}$	$\displaystyle=$	$\displaystyle 1+\log 3$
$\displaystyle V_{1}$	$\displaystyle=$	$\displaystyle 3+2\ \log 3$
$\displaystyle V_{2}$	$\displaystyle=$	$\displaystyle 8+4\ \log 3$

εκ των οποίων προκύπτουν οι εξής τιμές για τις σταθερές επιλύοντας ένα σύστημα τριών εξισώσεων με τρεις αγνώστους:

$\displaystyle c_{1}$	$\displaystyle=$	$\displaystyle 3+\log 3$
$\displaystyle c_{2}$	$\displaystyle=$	$\displaystyle-2$
$\displaystyle c_{3}$	$\displaystyle=$	$\displaystyle-1$

Επομένως, προκύπτει:

V_{k}\ =\ (3+\log 3)\ 2^{k}-k-2

(2.106)

από όπου με δύο αντίστροφους μετασχηματισμούς (δηλαδή $t_{k}=2^{V_{k}}$ και $T(n)=t_{\log n}$ ) σταδιακά προκύπτει ότι:

t_{k}\ =\ \frac{2^{3\times 2^{k}}\ \ 2^{\log 3\times 2^{k}}}{2^{k}\ \ 2^{2}}\ % =\ \frac{8^{2^{k}}\ \ 3^{2^{k}}}{2^{k+2}}

(2.107)

οπότε, τελικώς:

T(n)\ =\ \frac{2^{3n-2}\ \ 3^{n}}{n}

(2.108)

2.12 Δένδρο Αναδρομής

Αρκετές φορές η οπτικοποίηση μιας σχέσης αναδρομής μέσω ενός δένδρου αναδρομής (recursion tree) βοηθά στη κατανόηση του τι συμβαίνει, όταν η σχέση επαναλαμβάνεται. Αυτό μπορεί να βοηθήσει στην οργάνωση των πράξεων με τέτοιο τρόπο, έτσι ώστε να γίνει εκτίμηση του γενικού όρου.

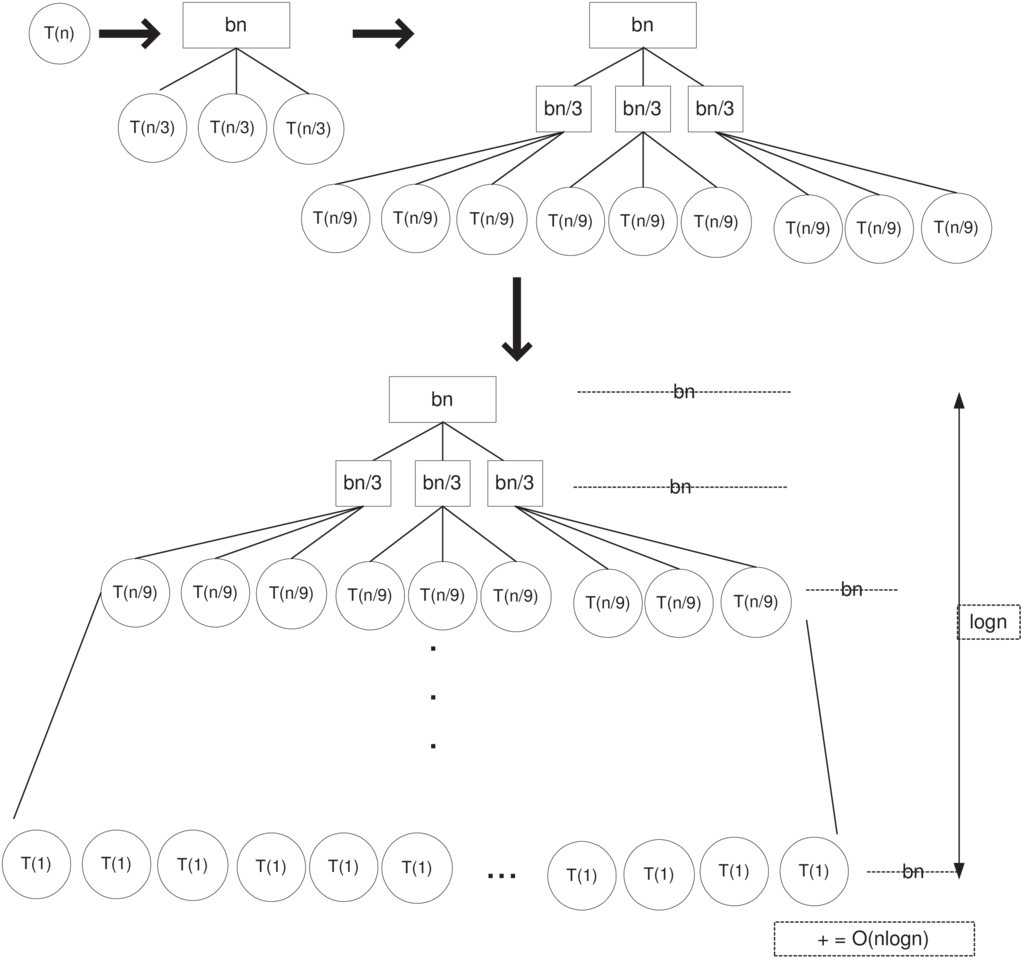
Έστω ότι έχουμε την αναδρομική σχέση $Τ_{n}=3Τ_{n/3}+bn,Τ_{0}=Τ_{1}=Τ_{2}=b$ , που εκφράζει το πλήθος των βημάτων που θα εκτελέσει ένας αλγόριθμος για είσοδο μεγέθους $n$ . Όπως φαίνεται και στο Σχήμα 2.5, για ένα στιγμιότυπο μεγέθους $n$ θα εκτελέσει $b n$ βήματα συν το πλήθος των βημάτων που θα εκτελέσει, για να επιλύσει τα τρία υποπροβλήματα μεγέθους $\frac{n}{3}$ . Κάθε τέτοιο υποπρόβλημα χρειάζεται $\frac{bn}{3}$ βήματα συν τα βήματα για την επίλυση των τριών υποπροβλημάτων μεγέθους $\frac{n}{9}$ , κοκ. Με αυτό τον τρόπο σχεδιάζεται το δένδρο αναδρομής, το οποίο θα έχει ύψος $\log_{3}n$ , αφού σε κάθε επίπεδο τα μεγέθη των προβλημάτων υποτριπλασιάζονται, ενώ για να φθάσουμε σε προβλήματα μεγέθους 1 χρειάζονται $\log_{3}n$ επίπεδα. Κάθε κόμβος του δένδρου αυτού αναπαριστά και ένα κόστος βημάτων. Αθροίζοντας όλα τα κόστη σε κάθε επίπεδο παρατηρείται ότι για κάθε επίπεδο το συνολικό κόστος είναι $b n$ . Συνεπώς, καταλήγουμε ότι αφού ο αλγόριθμος χρειάζεται $b n$ βήματα για κάθε επίπεδο, τότε συνολικά για τα $\log_{3}n$ επίπεδα θα χρειασθεί χρόνο Ο $(n\log n)$ .

2.13 Το Γενικό Θεώρημα

Το γενικό θεώρημα (master theorem) είναι ένας εναλλακτικός τρόπος επίλυσης αναδρομικών εξισώσεων. Αν γίνει κατανοητό στα λεπτά του σημεία, τότε είναι ένας εύκολος τρόπος στη χρήση του. Παραθέτουμε το θεώρημα χωρίς απόδειξη (στηρίζεται στο δένδρο αναδρομής).

Θεώρημα.
Έστω μία αναδρομική εξίσωση της μορφής:

T(n)\ =\ aT(n/b)+f(n)

(2.109)

όπου $a,b\geq 1$ , ενώ η $f(n)$ είναι μία ασυμπτωτικά θετική συνάρτηση. Τότε:

T(n)\ =\ \left\{\begin{array}[]{ll}{\Theta}(n^{\log_{b}a})&{\rm αν}\ f(n)={\rm O% }(n^{\log_{b}a-\epsilon}),\ \epsilon>0\\ {\Theta}(n^{\log_{b}a}\log n)&{\rm αν}\ f(n)={\Theta}(n^{\log_{b}a})\\ {\Theta}(f(n))&{\rm αν}\ f(n)={\Omega}(n^{\log_{b}a+\epsilon}),\ \epsilon>0,\ % af(\frac{n}{b})\leq cf(n),\ c<1\\ \end{array}\right.

(2.110)

$\Box$

Σημειώνεται ότι παρόμοιες αναδρομικές εξισώσεις προκύπτουν κατά την εφαρμογή της αλγοριθμικής μεθόδου Διαίρει και Βασίλευε. Στην περίπτωση αυτή, κατά τη φάση του Διαίρει προκύπτουν υποπίνακες με ακέραιο μέγεθος, δηλαδή υπεισέρχεται η συνάρτηση πάτωμα ή/και η συνάρτηση ταβάνι. Κατά την εφαρμογή του γενικού θεωρήματος αγνοούμε τις συναρτήσεις αυτές καθώς ασυμπτωτικά δεν αλλάζει τίποτε.

Με λίγα λόγια, το γενικό θεώρημα μας προτρέπει να συγκρίνουμε τη συνάρτηση $f(n)$ με την έκφραση $n^{\log_{b}a}$ . Αναλόγως με τη σχέση μεταξύ τους (ποιά είναι μικρότερη, μεγαλύτερη ή αν τυχόν είναι ίσες), τότε υιοθετούμε την αντίστοιχη εκδοχή. Προσοχή στο εξής σημείο. Δεν αρκεί απλώς μία εκ των δύο να είναι μικρότερη αλλά να είναι πολυωνυμικά μικρότερη. Λόγου χάριν, το $n^{2}$ είναι πολυωνυμικά μικρότερο από το $n^{3}$ , όπως και το $\sqrt{n}$ από το $n$ . Όμως, το $n$ δεν είναι πολυωνυμικά μικρότερο από το $n\log n$ , ούτε μπορούμε να συγκρίνουμε πολυωνυμικά τις εκφράσεις $n$ και $n^{1+\cos n}$ . Επομένως, το θεώρημα δεν εφαρμόζεται πάντοτε. Στη συνέχεια, θα εξετάσουμε αντίστοιχα παραδείγματα.

Έστω ότι δίνεται η συνάρτηση:

T(n)\ =\ 4T(n/2)+n

(2.111)

Ισχύει ότι $n^{\log_{b}a}=n^{\log_{2}4}=n^{2}>f(n)=n$ . Άρα, $\epsilon=1$ και ακολουθούμε το πρώτο σκέλος του θεωρήματος, δηλαδή $T(n)={\Theta}(n^{2})$ .

Έστω ότι δίνεται η συνάρτηση:

T(n)\ =\ 4T(n/2)+n^{2}

(2.112)

Ισχύει ότι $n^{\log_{b}a}=n^{\log_{2}4}=n^{2}=f(n)$ . Άρα, ακολουθούμε το δεύτερο σκέλος του θεωρήματος, οπότε $T(n)={\Theta}(n^{2}\log n)$ .

Έστω ότι δίνεται η συνάρτηση:

T(n)\ =\ 4T(n/2)+n^{3}

(2.113)

Ισχύει ότι $n^{\log_{b}a}=n^{\log_{2}4}=n^{2}<f(n)=n^{3}$ για $\epsilon=1$ . Άρα ακολουθούμε το τρίτο σκέλος του θεωρήματος. Πρέπει να αποδείξουμε την απαραίτητη συνθήκη του σκέλους αυτού. Έχουμε, λοιπόν, ότι: $\ af(n/b)=4(n/2)^{3}=\frac{1}{2}n^{3}$ , το οποίο θα πρέπει να είναι μικρότερο από $cn^{3}$ . Άρα αρκεί να ισχύει $c=1/2$ . Συνεπώς πράγματι μπορούμε να ακολουθήσουμε το τρίτο σκέλος, οπότε προκύπτει ότι $T(n)={\Theta}(n^{3})$ .

Ένα τελικό παράδειγμα όπου δεν μπορεί να εφαρμοσθεί το γενικό θεώρημα. Έστω η συνάρτηση:

T(n)\ =\ 4T(n/2)+n^{2}/\log n

(2.114)

Ισχύει ότι $n^{\log_{b}a}=n^{\log_{2}4}=n^{2}\ ?\ f(n)=n^{2}/\log n$ . Το ερωτηματικό τίθεται στην προηγούμενη σχέση, για να δηλώσει ότι αδυνατούμε να συγκρίνουμε πολυωνυμικά τις δύο εκφράσεις (για παράδειγμα, δεν υπάρχει κάποιο $\epsilon$ ). Έτσι, στο σημείο αυτό δεν μπορεί να υπάρξει πρόοδος, γιατί δεν είναι δυνατό να γίνει αναγωγή σε κάποια από τις τρεις κατηγορίες. Βέβαια, η αναδρομική αυτή εξίσωση έχει ήδη λυθεί με τη μέθοδο της επανάληψης.

2.14 Βιβλιογραφική Συζήτηση

Στο κεφάλαιο αυτό έγινε μία ταχεία παρουσίαση μερικών μαθηματικών εργαλείων που είναι χρήσιμα κατά την ανάλυση αλγορίθμων. Η παρουσίαση αυτή έγινε χωρίς αυστηρή προσέγγιση αλλά υπό τύπον υπενθύμισης. Το υλικό αυτό μπορεί να βρεθεί σε εισαγωγική μορφή σε βιβλία Διακριτών Μαθηματικών (Discrete Mathematics), όπως το βιβλίο [42] που εξετάζει κατά πλάτος πολλά αντικείμενα. Τα διδακτικά εγχειρίδια με μία εις βάθος προσέγγιση και πλούσιο σχετικό υλικό υπογράφονται (και) από τον Knuth [66, 88]. Ιδιαιτέρως, το βιβλίο [66] διακρίνεται για τη βαθειά του μαθηματική προσέγγιση. Το υλικό του κεφαλαίου αυτού παρουσιάζεται σε παρόμοια μορφή σε πολλά αντίστοιχα εγχειρίδια, όπως των Brassard-Bratley [19] και των Cormen-Leiserson-Rivest-Stein [34]. Συμπληρωματικά στοιχεία μπορούν να βρεθούν σχετικά με δυωνυμικούς συντελεστές στο βιβλίο του Bryant [24] και του Govinda Rao [65]. Απαιτητικό αλλά αξεπέραστο σε θεμελιώσεις ανάλυσης αλγορίθμων είναι το βιβλίο των Sedgewick-Flajolet [161].

Άπειρες είναι οι αναφορές στη βιβλιογραφία σχετικά με τους ασυμπτωτικούς συμβολισμούς. Στο βιβλίο του Knuth [66] αναφέρεται ότι ο συμβολισμός Ο προτάθηκε για πρώτη φορά το 1894 από το μαθηματικό Paul Bachmann [9]. Στο άρθρο [90] αναφέρεται το ιστορικό του καθορισμού του κάθε συμβολισμού, ενώ το άρθρο [156] βοηθά στην περαιτέρω κατανόησή τους. Η βιβλιογραφία σχετικά με την Υπολογιστική Πολυπλοκότητα είναι ιδιαίτερα εκτενής. Σημειώνεται το κλασικό βιβλίο των Garey-Johnson [51], όπου γίνεται μία κατά πλάτος παρουσίαση των προβλημάτων της κλάσης ΝΡ, καθώς και τα βιβλία του Παπαδημητρίου για μία γενική θεώρηση του αντικειμένου [102, 142].

Η Άσκηση 6 βασίζεται στο βιβλίο [169], που αποτελεί μία καλή εισαγωγική προσέγγιση στο αντικείμενο, ενώ οι Ασκήσεις 3-5 και 23-24 στο βιβλίο των Graham-Knuth-Patashnik [66], που αποτελεί μία τεράστια πηγή προβλημάτων. Η Άσκηση 7 έχει τεθεί στη Βαλκανική Ολυμπιάδα Πληροφορικής του 1997, η Άσκηση 18 βασίζεται στο άρθρο [94], ενώ η Άσκηση 28 βασίζεται στο άρθρο [53].

Τεχνικές επίλυσης αναδρομικών εξισώσεων βρίσκονται σε πλείστα διδακτικά βιβλία. Μεταξύ άλλων σημειώνονται τα κλασικά του είδους, όπως των Brassard-Bratley [19] και των Cormen-Leiserson-Rivest-Stein [34]. Συμπληρωματικά στοιχεία και ασκήσεις μπορούν να βρεθούν στα βιβλία του Govinda Rao [65], των Graham-Knuth-Patashnik [66], του Liu [104] και του Shaffer [169]. Λεπτομέρειες σχετικά με το γενικό θεώρημα μπορούν να βρεθούν στο άρθρο [11], καθώς και στα βιβλία [34, 35, 195]. Η Άσκηση 41 είναι μία γενίκευση του δημοφιλούς προβλήματος του Josephus, για το οποίο ιστορικά στοιχεία αναφέρονται στα βιβλία [66, 99], ενώ οι Ασκήσεις 42-43 βασίζονται επίσης στο πρόβλημα αυτό.

2.15 Ασκήσεις

1.

Η αρχή των περιστερώνων (Pigeonhole principle). Δεδομένων $n$ περιστερώνων και $m>n$ περιστεριών να αποδειχθεί ότι τουλάχιστον ένας περιστερώνας θα δεχθεί περισσότερο από ένα περιστέρι.
2.

Η αρχή του κουτιού του Dirichlet (Dirichlet box principle). Δεδομένων $n$ αντικειμένων και $m$ κουτιών να αποδειχθεί ότι κάποια κουτιά περιέχουν περισσότερο από $\lceil n/m\rceil$ αντικείμενα και κάποια κουτιά περιέχουν λιγότερο από $\lfloor n/m\rfloor$ αντικείμενα.
3.

Σε ένα καζίνο υπάρχει ρουλέτα με 1000 αριθμούς. Αν η ρουλέτα φέρει έναν αριθμό $n$ που διαιρείται με την ποσότητα $\lfloor\sqrt[3]{n}\rfloor$ , τότε ο παίκτης κερδίζει 5 ευρώ, αλλιώς χάνει 1 ευρώ. Ασυμπτωτικά, ο παίκτης θα κερδίσει ή θα χάσει;
4.

Να αποδειχθεί ότι η επόμενη έκφραση ισούται με $\lfloor x\rfloor$ ή με $\lceil x\rceil$ . Πότε εμφανίζεται το κάθε αποτέλεσμα;

$\left\lceil\frac{2x+1}{2}\right\rceil\ -\ \left\lceil\frac{2x+1}{4}\right% \rceil\ =\ \left\lfloor\frac{2x+1}{4}\right\rfloor$ (2.115)
5.
Να αποδειχθούν οι σχέσεις για $n, m$ ακεραίους θετικούς:
- –
  
  $n\ =\ \left\lfloor\frac{n}{m}\right\rfloor+\left\lfloor\frac{n-1}{m}\right% \rfloor+\ldots\left\lfloor\frac{n-m+1}{m}\right\rfloor$
- –
  
  $n\ =\ \left\lceil\frac{n}{m}\right\rceil+\left\lceil\frac{n-1}{m}\right\rceil+% \ldots\left\lceil\frac{n-m+1}{m}\right\rceil$
- –
  
  $\left\lfloor\frac{n}{m}\right\rfloor\ =\ \left\lceil\frac{n-m+1}{m}\right\rceil$
6.

Ένας άνδρας αποφασίζει να επισκεφθεί μία φίλη του που μένει 60 χλμ μακριά. Αρχίζει το ταξίδι οδηγώντας με ταχύτητα 60 χλμ/ώρα. Μετά από 1 χλμ πέφτει ο ενθουσιασμός του και αυτομάτως η ταχύτητα μειώνεται στα 59 χλμ/ώρα. Και πάλι, μετά από ένα 1 χλμ η ταχύτητα μειώνεται στα 58 χλμ/ώρα κοκ. Σε πόση ώρα θα φθάσει στο σπίτι της φίλης του;
7.

Δεδομένου ενός θετικού ακέραιου αριθμού $n$ , να βρεθούν όλοι οι θετικοί ακέραιοι $x$ (αν υπάρχουν) για τους οποίους ισχύει ότι ο αριθμός $x!$ έχει $n$ δεκαδικά ψηφία ακριβώς. Να υποτεθεί ότι $n\leq 150.000$ .
8.
Να αποδειχθεί ότι:
- –
  
  $n^{n/2}\leq n!\leq\frac{(n+1)^{n}}{2^{n}}$
9.
Να αποδειχθεί ότι:
- –
  
  $\sum_{i=k}^{n-1}{i\choose k}\ =\ {n\choose k+1}$
- –
  
  $\sum_{i=1}^{n}{n-i+1\choose k-i+1}\ =\ {n+1\choose k}$
- –
  
  ${r\choose m}\ {m\choose k}\ =\ {r\choose k}\ {r-k\choose m-k}$
10.

Να αποδειχθεί ότι για κάθε $n\geq 0$ και $0\leq k\leq n$ , η ποσότητα ${n\choose k}$ μεγιστοποιείται, όταν $k=\lfloor n/2\rfloor$ ή $k=\lceil n/2\rceil$ .
11.
Να αποδειχθεί ότι:
- –
  
  $(F_{n})^{2}\ =\ F_{n-1}\ F_{n+1}-(-1)^{n}$
- –
  
  $\sum_{i=0}^{n}F_{i}\ =\ F_{n+2}-1$
- –
  
  $\sum_{i=0}^{n}{\left(F_{i}\right)}^{2}\ =\ F_{n}\ F_{n+1}$
- –
  
  $F_{n}\ <\ \left(\frac{5}{3}\right)^{n}$
- –
  
  $F_{2n}\ =\ F_{n}\ F_{n+1}+F_{n-1}F_{n}$
- –
  
  $F_{2n+1}\ =\ {\left(F_{n+1}\right)}^{2}+{\left(F_{n}\right)}^{2}$
- –
  
  τα $F_{3n},F_{3n+1},F_{3n+2}$ είναι άρτιος, περιττός και άρτιος αριθμός, αντιστοίχως.
12.
Να υπολογισθούν οι ποσότητες:
- –
  
  $\sum_{i=\lfloor n/2\rfloor}^{n}\ \frac{1}{i}$
- –
  
  $\sum_{i=0}^{\lg n}\ 2^{i}$
- –
  
  $\sum_{i=0}^{\infty}\ \frac{i-1}{2^{i}}$
- –
  
  $\sum_{i=1}^{\infty}\ (2i+1)\ x^{2i}$
- –
  
  $\sum_{i=1}^{\infty}\ (-1)^{i}\ i/(4i^{2}-1)$
13.
Να υπολογισθούν τα αθροίσματα:
- –
  
  $\sum_{i=0}^{\infty}\frac{1}{4^{i}}$
- –
  
  $\sum_{i=0}^{\infty}\frac{i}{4^{i}}$
- –
  
  $\sum_{i=0}^{\infty}\frac{i^{2}}{4^{i}}$
- –
  
  $\sum_{i=0}^{\infty}\frac{i^{n}}{4^{i}}$
14.
Να υπολογισθούν οι ποσότητες:
- –
  
  $\sum_{i=1}^{n}\ (2i+1)/(i(i+1))$
- –
  
  $\sum_{i=0}^{n-1}\ H_{i}$
- –
  
  $\sum_{i=0}^{n}\ i\ H_{i}$
- –
  
  $\sum_{i=0}^{n-1}\ H_{i}/(i+1)(i+2)$
15.
Σε κάθε μία από τις επόμενες περιπτώσεις να βρεθούν οι συμβολισμοί Ο και Ω, καθώς επίσης να υπολογισθούν τιμές για τις σταθερές $c_{i}$ και $n_{0}$ .
- –
  
  $c_{1}\ n^{3}+c_{2}$
- –
  
  $c_{3}\ n\log n+c_{4}\ n$
- –
  
  $c_{5}\ 2^{n}+c_{6}\ n^{5}$
- –
  
  $c_{7}\ n!+c_{8}\ n^{3}$
16.
Σε κάθε μία από τις επόμενες περιπτώσεις να σημειωθεί αν ισχύει: $f=O(g(n))$ , $f=\Omega(g(n))$ ή $f=\Theta(g(n))$ .
- –
  
  $f(n)=\sqrt{n}$ $g(n)=\log^{3}n$
- –
  
  $f(n)=n^{1/2}$ $g(n)=5^{\log n}$
- –
  
  $f(n)=2^{n}$ $g(n)=2^{n+1}$
- –
  
  $f(n)=\sum_{i=1}^{n}i^{k}$ $g(n)=n^{k+1}$
17.

Να διαταχθούν κατά αύξουσα σειρά οι συναρτήσεις: $n,\sqrt{n},n^{1.5},n^{2},n\log n$ , $10,n\log\log n,n{\log}^{2}n,n^{3},n\log n^{2},1/n,2^{n},2^{n}/2,n^{2}\log n$ . Ποιές συναρτήσεις είναι της ιδίας τάξης;
18.
Δίνεται ο επόμενος ψευδοκώδικας. Να βρεθεί ο συμβολισμός Ω. Μπορεί να βρεθεί ο συμβολισμός Ο;
```
while (n>1)
   if (n mod 2 = 1) then
      n <-- 3*n+1;
   else
      n <-- n/2;
```

19.

Δίνονται τα επόμενα δύο τμήματα ψευδοκώδικα. Να βρεθεί ο συμβολισμός O.

for i <-- 0 to n do
   j <--i;
   while j<>0 do j <-- j div 2;

for i <-- 0 to n do
   j <--i;
   while (j mod 2 = 1) do j <-- j div 2;

20.

Δίνονται τα επόμενα δύο τμήματα κώδικα C. Να βρεθεί ο συμβολισμός Θ.

sum1=0;
for (i=1; i<=n; i*=2)
   for (j=1; j<=n; j++)
      sum1++;

sum2=0;
for (i=1; i<=n; i*=2)
   for (j=1; j<=i; j++)
      sum2++;

21.
Δίνεται το επόμενο τμήμα κώδικα C, όπου ο πίνακας A[0..n-1] περιέχει μία τυχαία διάταξη των αριθμών από 1 μέχρι n. Να βρεθεί ο συμβολισμός Θ.
```
sum3=0;
for (i=0; i<n; i++)
   for (j=0; A[j]!=i; j++)
      sum3++;
```
22.
Να αποδειχθεί ότι (αν) ισχύει:
- –
  
  $\log^{k}n$ = o $(n)$ για κάθε σταθερά $k$
- –
  
  $\log n!$ = Θ( $n\log n$ )
- –
  
  $2^{n}$ = Θ( $3^{n}$ )
23.

Να εκφρασθεί με συμβολισμό Ο το γινόμενο ( $\ln n+\gamma+{\rm O}(1/n)$ ) επί ( $n+{\rm O}(\sqrt{n})$ ).
24.
Να αποδειχθεί ότι ισχύουν οι επόμενες σχέσεις για $n\rightarrow\infty$ :
- –
  
  $1+\frac{2}{n}+{\rm O}(n^{-2})\ =\ \left(1+\frac{2}{n}\right)\left(1+{\rm O}(n^% {-2})\right)$
- –
  
  ${\rm O}\left({\left(\frac{n^{2}}{\log\log n}\right)}^{1/2}\right)\ =\ {\rm O}(% {\left\lfloor\sqrt{n}\right\rfloor}^{2})$
- –
  
  ${\rm e}^{(1+{\rm O}(1/n))^{2}}\ =\ {\rm e}+{\rm O}(1/n)$
25.
Να αποδειχθεί επαγωγικά ότι:
- –
  
  $\left(1+\frac{1}{1}\right)\cdot\left(1+\frac{1}{2}\right)\cdot\ldots\cdot\left% (1+\frac{1}{n}\right)\ =\ n+1$ για $n\geq 1$
- –
  
  $\left(1-\frac{1}{2^{2}}\right)\cdot\left(1-\frac{1}{3^{2}}\right)\cdot\ldots% \cdot\left(1-\frac{1}{n^{2}}\right)\ =\ \frac{n+1}{2n}$ για $n\geq 2$
- –
  
  $\prod_{i=0}^{n}\left(\frac{1}{2i+1}\cdot\frac{1}{2i+2}\right)\ =\ \frac{1}{(2n% +2)!}$ για $n\geq 0$
26.

Να αποδειχθεί επαγωγικά ότι το άθροισμα των γωνιών ενός κυρτού πολυγώνου με $n$ κορυφές είναι $(n-2)\cdot 180^{\rm o}$ .
27.

Να αποδειχθεί επαγωγικά ότι ένας τετραγωνικός πίνακας $2^{k}\times 2^{k}$ μπορεί να καλυφθεί πλήρως με πλακάκια που αποτελούνται από 3 τετράγωνα, όπως στο Σχήμα 2.6, εκτός από ένα μόνο τετράγωνο. Το Σχήμα 2.7 παρουσιάζει μια λύση για ένα στιγμιότυπο του προβλήματος όπου $k=3$ .

Σχήμα 2.6: Το πρόβλημα με τα πλακάκια.

Σχήμα 2.7: Παράδειγμα λύσης Άσκησης 27 όπου $k=3$ .
28.

Να αποδειχθεί επαγωγικά ότι κάθε κλάσμα $\frac{p}{q}$ , όπου $0<\frac{p}{q}<1$ μπορεί να παρασταθεί με τη λεγόμενη Αιγυπτιακή μορφή $\frac{p}{q}=\frac{1}{n_{1}}+\frac{1}{n_{2}}+\ldots\frac{1}{n_{m}}$ , όπου τα $n_{i}$ (για $1\leq i\leq m$ ) είναι θετικοί ακέραιοι που ικανοποιούν τη συνθήκη $n_{1}<n_{2}<\ldots<n_{m}$ .
29.
Από τις επόμενες γραμμικές αναδρομικές εξισώσεις ποιές είναι ομογενείς και ποιές όχι:
- –
  
  $t_{n}+2t_{n-1}+t_{n-2}=0$
- –
  
  $t_{n}={t_{n-1}}^{2}+{t_{n-2}}^{2}$
- –
  
  $t_{n}=\sqrt{t_{n-1}+t_{n-2}}$
- –
  
  $t_{n}=5t_{n-1}-6t_{n-3}+t_{n-5}$ .
30.
Να επιλυθούν οι επόμενες αναδρομικές εξισώσεις με τη μέθοδο της αντικατάστασης.
- –
  
  $t_{n}\ =\ b\ n^{2}+n\ t(n-1)$ , ενώ $t_{1}=a$
- –
  
  $t_{n}\ =\ b\ n^{k}+n\ t(n-1)$ , ενώ $t_{1}=a$
- –
  
  $t_{n}\ =\ 7\ n_{n/2}+n^{2}$ , ενώ $t_{1}=a$
- –
  
  $t_{n}\ =\ 7\ n_{n/3}+n^{2}$ , ενώ $t_{1}=t_{2}=a$
31.
Να επιλυθούν οι επόμενες αναδρομικές εξισώσεις με τη μέθοδο της επανάληψης θεωρώντας, όπου χρειασθεί, ότι το $n$ είναι δύναμη του 2.
- –
  
  $T(n)\ =\ c\ T(n-1)$ , όπου $T(0)=1$
- –
  
  $T(n)\ =\ n\ T(n-1)$ , όπου $T(0)=1$
- –
  
  $T(n)\ =\ 1+T(\lfloor n/2\rfloor)$ , όπου $T(1)=1$
- –
  
  $T(n)\ =\ 1+2\ T(\lfloor n/2\rfloor)$ , όπου $T(1)=1$
- –
  
  $T(n)\ =\ T(\lfloor n/2\rfloor)+\sqrt{n}$ , όπου $T(1)=1$
- –
  
  $T(n)\ =\ c\ \lceil\log n\rceil+T(\lceil n/2\rceil)$ , όπου $T(1)=0$
- –
  
  $T(n)\ =\ \lceil n\log n\rceil+T(\lceil n/2\rceil)$ , όπου $T(1)=0$ .
32.
Να επιλυθούν οι εξής ομογενείς γραμμικές αναδρομικές εξισώσεις με τη μέθοδο της χαρακτηριστικής εξίσωσης:
- –
  
  $t_{k}\ =\ 4\ t_{k-1}+5\ t_{k-2}$ , όπου $k\geq 2$ και $t_{0}=3,t_{1}=6$
- –
  
  $t_{k}\ =\ 3\ t_{k-1}+4\ t_{k-2}$ , όπου $k\geq 2$ και $t_{0}=0,t_{1}=1$
- –
  
  $t_{k}\ =\ t_{k-1}+t_{k-2}$ , όπου $k\geq 2$ και $t_{0}=0,t_{1}=1$
- –
  
  $t_{k}\ =\ 2\ t_{k-1}-2\ t_{k-2}$ , όπου $k\geq 2$ και $t_{0}=0,t_{1}=1$
- –
  
  $t_{k}\ =\ 5\ t_{k-1}-8\ t_{k-2}+4\ t_{k-3}$ , όπου $k\geq 3$ και $t_{0}=0,t_{1}=1,t_{2}=2$ .
33.
Να επιλυθούν οι εξής μη ομογενείς γραμμικές αναδρομικές εξισώσεις με τη μέθοδο της χαρακτηριστικής εξίσωσης:
- –
  
  $t_{k}\ =\ 2\ t_{k-1}+3^{n}$ , όπου $k\geq 1$
- –
  
  $t_{k}\ =\ 2\ t_{k-1}+(n+5)\ 3^{n}$ , όπου $k\geq 1$
- –
  
  $t_{k}\ =\ 2\ t_{k-1}+1$ , όπου $k\geq 1$ και $t_{0}=0$
- –
  
  $t_{k}\ =\ 2\ t_{k-1}+k$ , όπου $k\geq 1$
- –
  
  $t_{k}\ =\ 2\ t_{k-1}+k+2^{k}$ , όπου $k\geq 1$ και $t_{0}=0$ .
34.
Να επιλυθούν οι εξής αναδρομικές εξισώσεις με τη μέθοδο της αλλαγής μεταβλητής θεωρώντας, όπου χρειασθεί, ότι το $n$ είναι δύναμη του 2:
- –
  
  $T(n)\ =\ 2\ T(\lfloor\sqrt{n}\rfloor)+1$ , όπου $n>1$
- –
  
  $T(n)\ =\ 2\ T(\lfloor\sqrt{n}\rfloor)+\log n$ , όπου $n>1$
- –
  
  $T(n)\ =\ 4\ T(n/2)+n^{2}$ , όπου $n>1$
- –
  
  $T(n)\ =\ 2\ T(n/2)+n\log n$ όπου $n>1$
- –
  
  $T(n)\ =\ 3\ T(n/2)+c\ n$ , όπου $n>1$ και $c$ σταθερά.
35.
Να επιλυθούν οι εξής αναδρομικές εξισώσεις με τη μέθοδο του γενικού θεωρήματος, θεωρώντας, όπου χρειασθεί, την κατάλληλη μορφή του $n$ :
- –
  
  $T(n)\ =\ 2\ T(n/2)+\log n$ , όπου $n\geq 2$ και $T(1)=1$
- –
  
  $T(n)\ =\ 2\ T(\sqrt{n})+\log n$ , όπου $n\geq 4$ και $T(2)=1$
- –
  
  $T(n)\ =\ 9\ T(n/3)+n$ , όπου $n\geq 3$ και $T(1)=1$
- –
  
  $T(n)\ =\ T(2n/3)+1$ , όπου $n\geq 3$ και $T(1)=1$
- –
  
  $T(n)\ =\ 3\ T(n/4)+n\log n$ , όπου $n\geq 4$ και $T(1)=1$
- –
  
  $T(n)\ =\ 2\ T(n/2)+n\log n$ , όπου $n\geq 2$ και $T(1)=1$ .
36.
Να επιλυθούν οι εξής αναδρομικές εξισώσεις θεωρώντας, όπου χρειασθεί, ότι το $n$ είναι δύναμη του 2:
- –
  
  $T(n)\ =\ 5\ T(n/2)+(n\log n)^{2}$ , όπου $n\geq 2$ και $T(1)=1$
- –
  
  $T(n)=\frac{3}{2}\ T(n/2)-\frac{1}{2}\ T(n/4)-\frac{1}{n}$ , όπου $n\geq 3$ και $T(1)$ =1, $T(2)$ = $\frac{3}{2}$
- –
  
  $t_{k}\ =\ t_{k-1}+t_{k-3}-t_{k-4}$ , όπου $k\geq 4$ και $t_{k}=k$ για $0\leq k\leq 3$
- –
  
  $t_{k}\ =\ 1/(4-t_{k-1})$ , όπου $k>1$ και $t_{1}=1/4$ .
37.
Να επιλυθούν οι εξής αναδρομικές εξισώσεις:
- –
  
  $t_{k}\ =\ t_{k-1}+2\ t_{k-2}-2\ t_{k-3}$ , όπου $k\geq 3$ και $t_{k}=9k^{2}-15k+106$ για $0\leq k\leq 2$
- –
  
  $t_{k}\ =\ (1+t_{k-1})/t_{k-2}$ , όπου $t_{0}=a$ και $t_{1}=b$
- –
  
  $2t_{k}\ =\ k\ t_{k-1}+3\ k!$ , όπου $t_{0}=5$
- –
  
  $t_{k}\ =\ t_{k-m}+1$ για $k\geq m$ και $t_{k}\ =\ k$ για $0\leq k\leq m$
38.

Για δύο αλγορίθμους δίνονται οι αντίστοιχες αναδρομικές εξισώσεις: $T_{1}(n)$ $=7\ T_{1}(n/2)+n^{2}$ και $T_{2}(n)=a\ T_{2}(n/4)+n^{2}$ . Για ποιες τιμές του $a$ ο δεύτερος αλγόριθμος είναι ασυμπτωτικά ταχύτερος του πρώτου;
39.

Να βρεθεί το πλήθος των τρόπων που μπορούμε να ανεβούμε μία σκάλα με $n$ σκαλοπάτια, αν είναι δυνατόν σε κάθε βήμα να ανεβαίνουμε είτε 1 σκαλοπάτι είτε 2 σκαλοπάτια. Για παράδειγμα, μία σκάλα 3 σκαλοπατιών μπορούμε να την ανεβούμε με 3 τρόπους: 1-1-1, 1-2, 2-1.
40.

Σε ένα πίνακα μεγάλου μεγέθους αρχικά τα τετράγωνα είναι κενά. Στην πρώτη κίνηση μαυρίζεται ένα τετράγωνο, όπως φαίνεται στο Σχήμα 2.8. Στη συνέχεια μαυρίζεται το τετράγωνο προς τα επάνω, κάτω, αριστερά και δεξιά. Στην επόμενη κίνηση, για κάθε από τα μαύρα τετράγωνα και πάλι μαυρίζουμε τα τετράγωνα προς τα επάνω, κάτω, αριστερά και δεξιά. Από πόσα μαύρα τετράγωνα αποτελείται το μαύρο σχήμα στη $n$ -οστή κίνηση;

Σχήμα 2.8: Το πρόβλημα με τα μαύρα τετράγωνα.
41.

Μία συμμορία από $n$ ληστές στην Άγρια Δύση περικυκλώνεται από το απόσπασμα του σερίφη. Οι ληστές έχουν μόνο ένα άλογο για να διαφύγουν. Έτσι συμφωνούν στην εξής μέθοδο επιλογής του τυχερού που θα πάρει το άλογο και θα σωθεί. Οι ληστές σχηματίζουν ένα κύκλο, ο αρχηγός αντιστοιχίζεται στον αριθμό 1 και η αρίθμηση συνεχίζει ωρολογιακά. Σε ένα καπέλο τοποθετούν $n$ λαχνούς με αριθμούς από 1 ως το $n$ . Ο αρχηγός τραβά ένα λαχνό με τον αριθμό, έστω, $i$ . Αυτό σημαίνει ότι ο $i$ -οστός ληστής πρέπει να εξαιρεθεί. Η διαδικασία των εξαιρέσεων του $i$ -οστού ληστή συνεχίζεται θεωρώντας για αρχή της καινούργιας αρίθμησης τον επόμενο ληστή αυτού που μόλις εξαιρέθηκε. Αυτός που μένει τελευταίος παίρνει το άλογο, όλα τα κλοπιμαία και φεύγει. Να σχεδιασθεί ένας αλγόριθμος υλοποίησης της μεθόδου. Να βρεθεί μέσω αναδρομικής εξίσωσης αυτός που θα αποφύγει την εξαίρεση, δεδομένων των $i$ και $n$ .
42.

Σε ένα κύκλο τοποθετούνται $2n$ άτομα. Τα πρώτα $n$ άτομα είναι οι «καλοί», ενώ τα επόμενα $n$ είναι οι «κακοί». Δεδομένου του $n$ , να βρεθεί ένα $m$ τέτοιο ώστε, αν εξαιρούμε από τον κύκλο κάθε $m$ -οστό άτομο, στο τέλος θα μείνουν μόνο οι «καλοί».
43.

Σε ένα κύκλο τοποθετούνται 10 άτομα και εξαιρείται από τον κύκλο κάθε $m$ -οστό άτομο (όπου το $m$ οποιοσδήποτε ακέραιος). Να αποδειχθεί ότι δεν είναι δυνατόν τα τρία πρώτα άτομα που θα εξαιρεθούν να είναι ο 10ος, ο $k$ -οστός και ο $(k+1)$ -οστός (με τη συγκεκριμένη σειρά), για οποιοδήποτε $k$ .