Κεφάλαιο 6Αλγοριθμικές Τεχνικές
Υπάρχουν κάποιες βασικές και θεμελιώδεις τεχνικές που μπορούμε να χρησιμοποιήσουμε για την αλγοριθμική επίλυση ενός προβλήματος. Τέτοιες τεχνικές αποτελούν μία καλή εργαλειοθήκη για την αλγοριθμική επίλυση προβλημάτων και είναι πάντα οι πρώτες που εφαρμόζουμε σε περίπτωση που αντιμετωπίζουμε κάποιο πρόβλημα, πριν χρησιμοποιήσουμε πιο προχωρημένες τεχνικές ή λύσεις προσαρμοσμένες σε αυτό. Οι τεχνικές που θα παρουσιαστούν σε αυτό το κεφάλαιο είναι οι εξής:
- Εξάντληση
-
(brute force). Είναι πάντοτε η πρώτη σκέψη για την επίλυση ενός προβλήματος. Η ιδέα είναι να παράγεις με έναν δομημένο τρόπο όλες τις λύσεις σε ένα πρόβλημα και να ελέγχεις αν έχουν την επιθυμητή ιδιότητα (π.χ. κόστος μικρότερο από ένα προκαθορισμένο κατώφλι). Βεβαίως υπάρχουν προβλήματα στα οποία αυτή είναι εκ φύσεως η μόνη λύση. Για παράδειγμα, αν θέλαμε όλες τις εξάδες του ΛΟΤΤΟ θα έπρεπε προφανώς να τις παράγουμε όλες. Από την άλλη, αν θέλαμε να ταξινομήσουμε έναν πίνακα μεγέθους , θα ήταν μάλλον ασύμφορο να παράγουμε όλες τις μεταθέσεις των θέσεων του πίνακα και για καθεμιά να ελέγχουμε αν ο προκύπτων πίνακας είναι ταξινομημένος ή όχι, όπως θα απαιτούσε η συγκεκριμένη μέθοδος.
- Άπληστη Μέθοδος
-
(greedy method). Το βασικό χαρακτηριστικό αυτής της μεθόδου είναι η αυξητική παραγωγή της λύσης κάνοντας κάθε φορά μία μη αντιστρεπτή άπληστη επιλογή ως προς κάποιο κριτήριο. Είναι μία τεχνική εξαιρετικά ισχυρή που οδηγεί σε απλούς και αποδοτικούς αλγορίθμους για αρκετά προβλήματα αλλά προφανώς όχι για όλα. Ένα γνωστό πρόβλημα είναι αυτό της εύρεσης του ελαχίστου ζευγνύοντος δένδρου, όπου υπάρχουν οι γνωστοί άπληστοι αλγόριθμοι των Prim και Kruskal.
- Διαίρει και Βασίλευε
-
(divide and conquer). Η βασική ιδέα αυτής της εξαιρετικά ισχυρής τεχνικής είναι η διαίρεση του προβλήματος σε υποπροβλήματα και έπειτα, αφού λυθεί το καθένα ανεξάρτητα από το άλλο, ο συνδυασμός αυτών των λύσεων σε μία μεγαλύτερη λύση. Κλασικό παράδειγμα αυτής της τεχνικής είναι η επίλυση του προβλήματος της ταξινόμησης ενός πίνακα στοιχείων χρησιμοποιώντας τον αλγόριθμο της γρήγορης ταξινόμησης (quicksort) ή τον αλγόριθμο της συγχώνευσης (mergesort).
- Δυναμικός Προγραμματισμός
-
(dynamic programming). Αυτή η εξαιρετικά χρήσιμη τεχνική στην ουσία είναι η τεχνική διαίρει και βασίλευε συνδυασμένη με την απομνημόνευση των ενδιάμεσων αποτελεσμάτων. Επί της ουσίας, η επίλυση των υποπροβλημάτων δεν γίνεται ανεξάρτητα αλλά υπάρχει κάποια αλληλεπίδραση. Ένα κλασσικό παράδειγμα εφαρμογής αυτής της τεχνικής είναι το πρόβλημα της μακρύτερης κοινής υποακολουθίας δύο ακολουθιών.
- Οπισθοδρόμηση
-
(backtracking). Η οπισθοδρόμηση είναι μία γενική τεχνική για εύρεση λύσεων κυρίως σε προβλήματα ικανοποίησης περιορισμών. Το βασικό χαρακτηριστικό αυτών των προβλημάτων είναι η δυνατότητα αυξητικής κατασκευής των υποψήφιων λύσεων με τέτοιο τρόπο, ώστε να είναι δυνατός ο έλεγχος για το αν μία μερική λύση (το τμήμα της λύσης που έχει κατασκευαστεί) δεν μπορεί να οδηγήσει σε μία συνολική λύση και, άρα, μπορούμε να εγκαταλείψουμε την κατασκευή της. Κλασικό παράδειγμα εφαρμογής αυτής της τεχνικής είναι το πρόβλημα τοποθέτησης βασιλισσών σε μία σκακιέρα .
- Διακλάδωση και Περιορισμός
-
(branch and bound). Αποτελεί μία γενική αλγοριθμική προσέγγιση για επίλυση συνδυαστικών προβλημάτων βελτιστοποίησης. Ένας τέτοιου τύπου αλγόριθμος εκτελεί μία συστηματική απαρίθμηση όλων των υποψήφιων λύσεων εκτελώντας μία αναζήτηση στον χώρο των λύσεων. Πιο συγκεκριμένα, θεωρούμε ότι οι υποψήφιες λύσεις αναπαρίστανται με ένα δένδρο, όπου η ρίζα του αντιστοιχεί σε όλες τις δυνατές λύσεις. Ο αλγόριθμος εξερευνά αυτό το δένδρο με τέτοιο τρόπο, ώστε για κάθε διακλάδωση (branch) γίνεται ένας έλεγχος σε σχέση με ένα κάτω ή/και άνω φράγμα που αφορά τη βέλτιστη λύση (bound) και, αν βρεθεί ότι σε αυτή τη διακλάδωση δεν υπάρχει λύση που να μπορεί να οδηγήσει στη βέλτιστη, τότε δεν συνεχίζουμε βαθύτερα σε αυτό τον κλάδο αλλά προχωράμε σε άλλο κλάδο. Το πρόβλημα του περιοδεύοντος πωλητή αποτελεί ένα κλασσικό παράδειγμα εφαρμογής της μεθόδου. Συνήθως εφαρμόζεται σε προβλήματα βελτιστοποίησης.
Αν θέλαμε να αναφέρουμε μία σχέση μεταξύ αυτών των τεχνικών, θα λέγαμε ότι οι τεχνικές της οπισθοδρόμησης και της διακλάδωσης και περιορισμού αποτελούν βελτιώσεις της τεχνικής της εξάντλησης. Η τεχνική του δυναμικού προγραμματισμού αποτελεί επέκταση της τεχνικής διαίρει και βασίλευε - χωρίς αυτό, βεβαίως, να σημαίνει ότι αν χρησιμοποιήσουμε την τεχνική διαίρει και βασίλευε σε ένα πρόβλημα τότε θα οδηγηθούμε σε καλύτερη λύση με τη μέθοδο του δυναμικού προγραμματισμού. Σε πολλά προβλήματα η απομνημόνευση των λύσεων που προσφέρει ο δυναμικός προγραμματισμός πολύ απλά δεν χρειάζεται.
Σε αυτό το κεφάλαιο θα κάνουμε μία μικρή εισαγωγή σε κάθε τεχνική μέσω ενός προβλήματος και, τέλος, θα μελετήσουμε τρία προβλήματα. Θα τα επιλύσουμε με εναλλακτικούς τρόπους, όπου κάθε φορά θα προχωρούμε σε εξυπνότερες επιλογές και αποδοτικότερους αλγορίθμους. Προσέξτε ότι δεν υπάρχει κάποιος μπούσουλας για το ποια τεχνική θα πρέπει να χρησιμοποιούμε για κάθε πρόβλημα. Αυτή την διαίσθηση μπορείτε να την αποκτήσετε μόνο με εμπειρία και με κάποιους κανόνες που, βεβαίως, έχουν και τις εξαιρέσεις τους.
6.1 Αλγοριθμικές Τεχνικές
Κάνουμε μία απλή εισαγωγή σε κάθε τεχνική μέσα από ένα αντιπροσωπευτικό πρόβλημα.
6.1.1 Εξάντληση
Για αυτή την τεχνική θα δούμε ένα μάλλον απλό γεωμετρικό πρόβλημα. Στο πρόβλημα του εγγύτερου ζεύγους μας δίνονται σημεία στον δισδιάστατο χώρο και μας ζητείται να βρούμε το ζεύγος σημείων με την μικρότερη ευκλείδια απόσταση (Σχήμα 6.1). Το πρόβλημα αυτό γενικεύεται σε πολλές διαστάσεις με προφανή τρόπο αλλά εμείς θα εστιάσουμε μόνο στις δύο διαστάσεις.
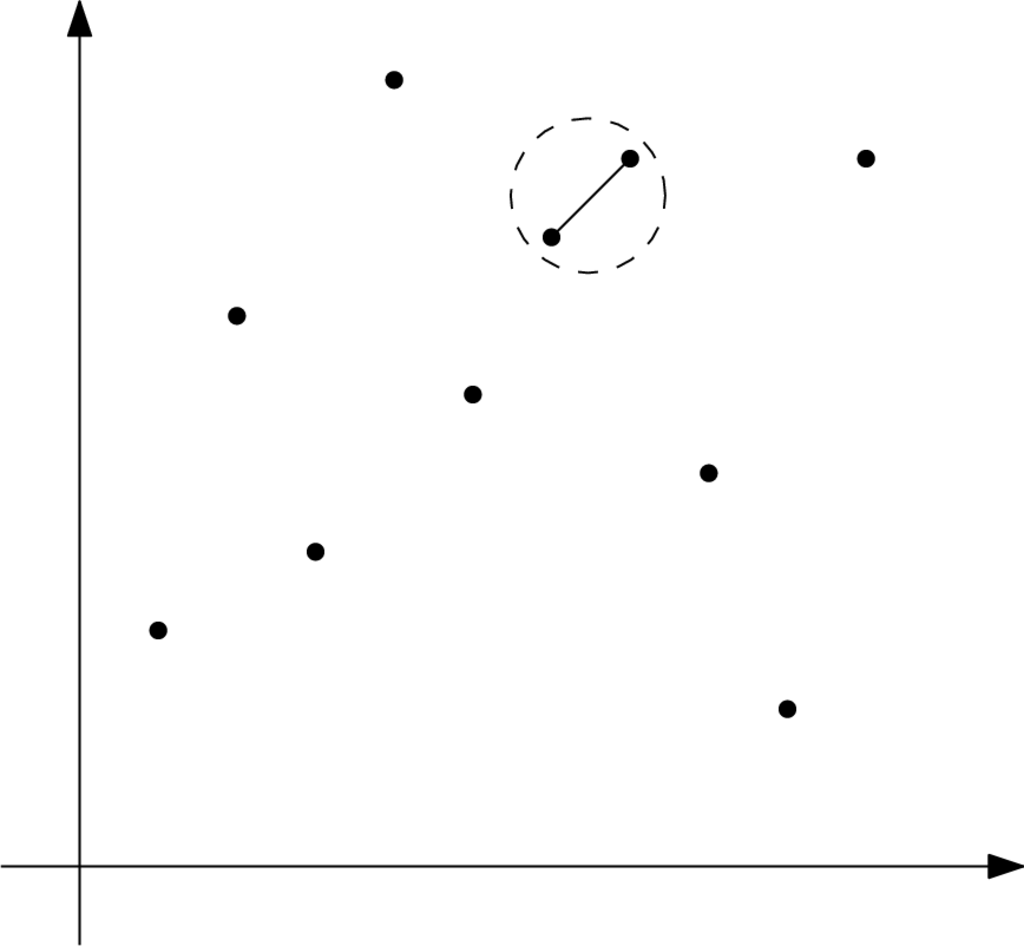
Αντιμέτωποι με ένα πρόβλημα, πάντα το πρώτο που κοιτάμε είναι την προφανή λύση, δηλαδή την εξάντληση. Έπειτα, με βάση και τη γνώση που έχουμε αποκομίσει για το πρόβλημα προχωράμε σε περισσότερο αποδοτικές μεθόδους. Έστω λοιπόν δύο σημεία του χώρου και . Τότε η μεταξύ τους ευκλείδια απόσταση δίνεται από τον τύπο:
Στην εξάντληση προσπαθούμε να βρούμε τη λύση με τον πιο άμεσο τρόπο: απλά κοιτάμε όλες τις λύσεις και επιλέγουμε αυτή που μας ικανοποιεί. Στην προκειμένη περίπτωση θα δημιουργήσουμε όλες τις δυνατές λύσεις, δηλαδή θα υπολογίσουμε τις αποστάσεις μεταξύ όλων των δυνατών ζευγών και θα επιλέξουμε την ελάχιστη.
Επομένως, ο αλγόριθμος ξεκινά υπολογίζοντας την απόσταση μεταξύ του και των κρατώντας κάθε φορά μία απόσταση, αυτή που είναι ελάχιστη μέχρι την συγκεκριμένη στιγμή εκτέλεσης του αλγόριθμου. Έπειτα, υπολογίζει τις αποστάσεις μεταξύ του και του και συνεχίζει μέχρι να υπολογίσει την απόσταση μεταξύ του και του .
Η ορθότητα του αλγορίθμου είναι προφανής. Ποια είναι όμως η απόδοση του αλγορίθμου; Προσέξτε ότι έχουμε περιγράψει τον αλγόριθμο με φυσική γλώσσα και μάλιστα με έναν μάλλον μη τυπικό τρόπο. Εντούτοις, είναι μάλλον εύκολο να καταλάβουμε ότι η απόδοση του αλγορίθμου καθορίζεται από το πλήθος των υπολογισμών αποστάσεων. Αφού για κάθε σημείο κάνουμε συγκρίσεις, το συνολικό πλήθος τους είναι:
Αυτός ο αλγόριθμος έχει τετραγωνική πολυπλοκότητα. Θα δούμε στο 6.1.3 ότι αυτή η πολυπλοκότητα μπορεί να μειωθεί σε .
Ο ίδιος ακριβώς αλγόριθμος θα μπορούσε να χρησιμοποιηθεί και για να λύσει το πρόβλημα σε περισσότερες διαστάσεις από . Σημειώστε μόνο ότι σε περισσότερες διαστάσεις ο υπολογισμός της απόστασης γίνεται ακριβότερος.
6.1.2 Άπληστη Μέθοδος
Σε αυτή τη μέθοδο η βασική αρχή είναι η αυξητική κατασκευή μίας λύσης σε ένα δοθέν πρόβλημα, έτσι ώστε σε κάθε βήμα της κατασκευής αυτής να κάνουμε μία άπληστη επιλογή - μία επιλογή, δηλαδή, που να μεγιστοποιεί το όφελός μας σε εκείνο το βήμα του αλγορίθμου. Συνήθως, η ύπαρξη μίας αποδοτικής άπληστης λύσης για ένα πρόβλημα υποδηλώνει ότι το πρόβλημα αυτό έχει μία εξαιρετική εσωτερική δομή. Επιπλέον, μία βασική προϋπόθεση για την εφαρμογή της μεθόδου σε ένα πρόβλημα είναι ότι η βέλτιστη λύση για αυτό το πρόβλημα εμπεριέχει τη βέλτιστη λύση για κάθε υποπρόβλημα. Τέλος, θα πρέπει να είμαστε προσεκτικοί ως προς το κριτήριο που θα εφαρμόσουμε την απληστία μιας και είναι κρίσιμης σημασίας για την επιτυχία της μεθόδου.
Ένα κλασσικό παράδειγμα εφαρμογής αυτής της τεχνικής είναι το πρόβλημα των ρέστων. Ας υποθέσουμε λοιπόν ότι έχουμε ένα σύνολο από κέρματα και θέλουμε με αυτά τα κέρματα να φτάσουμε ένα ποσό. Ας υποθέσουμε ότι το σύνολο των κερμάτων που έχουμε στη διάθεσή μας είναι το και ότι θέλουμε να φτάσουμε το ποσό των 188 λεπτών. Υπάρχουν διάφοροι τρόπο να το πετύχεις αυτό, π.χ. να χρησιμοποιήσουμε 188 κέρματα του ενός λεπτού. Το πρόβλημα αποκτά ενδιαφέρον όταν κάνουμε την εξής ερώτηση: Ποιο είναι το ελάχιστο πλήθος κερμάτων που μπορούμε να χρησιμοποιήσουμε, ώστε να φτάσουμε σε ένα δοθέν ποσό ;
Με δεδομένο ότι είναι ένα πρόβλημα ελαχιστοποίησης, θα προσπαθήσουμε να χρησιμοποιήσουμε την άπληστη μέθοδο. Το πρώτο πρόβλημα στην εφαρμογή αυτής της μεθόδου είναι η επιλογή του κριτηρίου απληστίας. Το προφανές κριτήριο σε αυτή την περίπτωση είναι να προσπαθούμε σε κάθε βήμα να επιλέγουμε το νόμισμα με την μέγιστη τιμή που να χωρά στο υπολειπόμενο ποσό. Θα μπορούσε όμως κάποιος να επιλέξει κάτι πιο περίεργο, όπως για παράδειγμα τη χρήση του νομίσματος με τη μέγιστη τιμή που να διαιρεί τέλεια το υπολειπόμενο ποσό. Μπορεί να φαίνεται περίεργο κριτήριο αλλά έχει μία (έστω και περίεργη) λογική, όπως θα δούμε παρακάτω. Για την ώρα, θα χρησιμοποιήσουμε το κριτήριο το οποίο μας βγαίνει πιο φυσικά (η διαίσθησή μας οδηγεί εκεί).
Ποιός είναι, λοιπόν, ο αλγόριθμος με βάση το συγκεκριμένο κριτήριο απληστίας. Πολύ απλά, χρησιμοποίησε το μεγαλύτερο νόμισμα που χωρά στο υπολειπόμενο ποσό μέχρι αυτό να φτάσει στο . Για παράδειγμα, για να φτάσουμε στα 188 λεπτά χρησιμοποιούμε αρχικά το νόμισμα με τη μεγαλύτερη τιμή, δηλαδή το νόμισμα με την τιμή . Από τα 138 λεπτά που απομένουν επαναλαμβάνοντας την ίδια διαδικασία 2 φορές χρησιμοποιούμε άλλα δύο νομίσματα με τιμή , ενώ το υπολειπόμενο ποσό είναι . Στην επόμενη επανάληψη χρησιμοποιούμε ένα νόμισμα των με το υπολειπόμενο ποσό να είναι ίσο με 18. Επαναλαμβάνοντας αυτή τη διαδικασία μέχρι το υπολειπόμενο ποσό να είναι βρίσκουμε ότι το ελάχιστο πλήθος κερμάτων που χρειαζόμαστε αναπαρίσταται από το πολυσύνολο . Επομένως, χρειαζόμαστε συνολικά κέρματα και όχι λιγότερα.
Ποια είναι η πολυπλοκότητα του αλγόριθμου; Ουσιαστικά, αν έχουμε κέρματα και θέλουμε να φτάσουμε στο ποσό των λεπτών τότε ένα τετριμμένο πάνω φράγμα θα ήταν ίσο με (φανταστείτε ότι αν και έχουμε ένα κέρμα του ενός λεπτού, τότε για λεπτά θα χρειαζόμασταν επαναλήψεις). Ένα καλύτερο φράγμα θα εμπεριείχε και τις τιμές και μάλλον δεν έχει νόημα να ασχοληθούμε. Προσέξτε ότι αυτό το χονδροειδές άνω φράγμα υποδηλώνει ότι ενδεχομένως (πράγματι ισχύει αυτό) ο αλγόριθμος να είναι ψευδοπολυωνυμικός, δηλαδή η πολυπλοκότητα του δεν είναι μία πολυωνυμική συνάρτηση της εισόδου παρόλο που φαίνεται ότι είναι (εξού και το ψευδό-). Αυτό ισχύει, αφού το αναπαρίσταται από λέξεις μνήμης (bits για την ακρίβεια), ενώ η πολυπλοκότητα δεν περιέχει το αλλά το .
Αυτή ήταν η εύκολη ερώτηση. Συνήθως, η πολυπλοκότητα στους άπληστους αλγόριθμους είναι εύκολο να βρεθεί. Η δυσκολία είναι να αποδείξουμε ότι ο αλγόριθμος είναι ορθός, δηλαδή ότι πράγματι παράγει τη βέλτιστη λύση. Καταρχάς, ο αλγόριθμός μας δεν είναι βέλτιστος (!!!) για οποιοδήποτε σύνολο κερμάτων. Για παράδειγμα, για το σύνολο κερμάτων ο αλγόριθμος δεν δίνει τη βέλτιστη λύση. Για παράδειγμα, για το ποσό των λεπτών η βέλτιστη λύση είναι η χρήση τριών κερμάτων των λεπτών, ενώ ο αλγόριθμος θα επέστρεφε το πολυσύνολο με κέρματα. Στην πραγματικότητα, ο άπληστος είναι βέλτιστος για κανονικά σύνολα κερμάτων [144] που έχουν συγκεκριμένες ιδιότητες. Προσέξτε, επίσης, ότι στο συγκεκριμένο παράδειγμα, για τη βέλτιστη λύση, όποιο ποσό και να πάρετε που να προκύπτει από τα τρία κέρματα πάλι θα βρείτε βέλτιστη λύση. Συγκεκριμένα, για λεπτά χρειαζόμαστε νόμισμα, ενώ για λεπτά χρειαζόμαστε δύο νομίσματα των , που είναι επίσης βέλτιστο. Από την άλλη, στη λύση που έδωσε ο άπληστος αλγόριθμος δεν ισχύει αυτό, αφού για το απαιτούνται νομίσματα, τα , και που προφανώς δεν είναι βέλτιστο (προσοχή ότι τα υποπροβλήματα που επιλέγουμε πρέπει να επιλύονται από τη λύση του μεγαλύτερου προβλήματος, δηλαδή των λεπτών).
Εμείς θα δώσουμε μία απόδειξη ορθότητας για το συγκεκριμένο σύνολο κερμάτων .
Θεώρημα 6.1.
Ο άπληστος αλγόριθμος είναι βέλτιστος για το σύνολο κερμάτων και για οποιοδήπτε ποσό .
Proof.
Θα χρησιμοποιήσουμε ένα επιχείρημα ανταλλαγής. Έστω η λύση με λύση με κέρματα που προτείνει ο άπληστος αλγόριθμος σε φθίνουσα σειρά κερμάτων, δηλαδή . Έστω και η βέλτιστη λύση , όπου η λύση είναι , όπου τα κέρματα είναι πάλι σε φθίνουσα σειρά και έστω ότι . Έστω ότι με βάση τη φθίνουσα σειρά, ο πρώτος δείκτης κατά σειρά στον οποίο δεν συμφωνούν οι δύο λύσεις είναι το -ιοστό, δηλαδή , αν και , και έστω ότι .
Καταρχάς, θα ισχύει ότι μιας και ο βέλτιστος αλγόριθμος επιλέγει πάντα το μεγαλύτερο σε αξία κέρμα. Θα φτιάξουμε έναν καινούργιο βέλτιστο , έτσι ώστε να χρησιμοποιεί ακόμα λιγότερα κέρματα από τον , κάτι που είναι άτοπο βέβαια αφού ο είναι ήδη βέλτιστος. Επομένως, θα καταλήγουμε στο συμπέρασμα ότι ο και ο συμπίπτουν. Αντικαθιστούμε το με το . Βεβαίως η καινούργια ακολουθία κερμάτων δεν δίνει το ποσό αλλά κάτι παραπάνω. Η ερώτηση, λοιπόν, είναι: Μπορούμε να αφαιρέσουμε κάποια νομίσματα από την υποακολουθία , έτσι ώστε να πάρουμε πάλι ως αποτέλεσμα το ; Η απάντηση είναι θετική για αυτό το σύνολο νομισμάτων.
Για να το δούμε αυτό θα πάρουμε όλες τις περιπτώσεις νομισμάτων. Έστω, λοιπόν, ότι . Αυτό σημαίνει ότι και θα πρέπει αναγκαστικά να ισχύει ότι , ώστε να είμαστε σε θέση και με άλλα ενδεχομένως νομίσματα (αξίας στην ) να φτάσουμε την τιμή . Επομένως, διώχνουμε και το νόμισμα και έχουμε μία νέα λύση με ένα κέρμα λιγότερο. Έστω ότι . Μία περίπτωση είναι να ισχύει , οπότε αναγκαστικά πρέπει να έχουμε τουλάχιστον ακόμα νομίσματα αξίας και, άρα, αν τα διώξουμε παίρνουμε τη βέλτιστη λύση με νομίσματα λιγότερα. Αν , τότε αν , θα πρέπει επίσης και (θυμηθείτε ότι τα νομίσματα στις λύσεις είναι σε φθίνουσα σειρά) για να καλυφθεί το νόμισμα των και άρα κατασκευάζουμε τη λύση με τρία νομίσματα λιγότερα. Αν επίσης ισχύει ότι , τότε αν στην υποακολουθία υπάρχει νόμισμα αξίας , το διώχνουμε και αυτό και κατασκευάζουμε μία λύση με δύο λιγότερα νομίσματα από την . Αν δεν υπάρχει νόμισμα αξίας σε αυτή την υποακολουθία, τότε σημαίνει ότι και άρα μπορούμε να αντικαταστήσουμε τα νομίσματα με ένα νόμισμα αξίας και, επομένως, η νέα λύση θα έχει ένα νόμισμα λιγότερο. Για να το ξεκαθαρίσουμε, σε αυτή την περίπτωση η λύση θα είναι . Στις περιπτώσεις , και δουλεύουμε με τον ίδιο τρόπο για την κατασκευή της λύσης που είναι πάντα καλύτερη από την . ∎
Η απόδειξη αυτή δεν ισχύει για άλλα σύνολα, όπως το σύνολο νομισμάτων . Σε αυτή την περίπτωση, η τελευταία παράγραφος της απόδειξης δεν ισχύει, αφού το επιχείρημα που χρησιμοποιούμε για κατασκευή λύσεων καλύτερης της βέλτιστης παύει να ισχύει πια.
Ένας άλλος τρόπος απόδειξης που μπορούμε να χρησιμοποιήσουμε για την απόδειξη ορθότητας των άπληστων αλγόριθμων εκτός του επιχειρήματος ανταλλαγής είναι η επαγωγή στα βήματα του αλγορίθμου. Στην παραπάνω περίπτωση θα θεωρούμε ότι ο άπληστος δίνει τη σωστή λύση για όλα τα ποσά μέχρι το και μετά θα δείχναμε ότι αυτό θα ίσχυε και για το προφανώς παίρνοντας αντίστοιχες περιπτώσεις για κάθε νόμισμα, όπως και παραπάνω.
6.1.3 Διαίρει και Βασίλευε
θα δούμε πως μπορούμε να μειώσουμε την πολυπλοκότητα για το πρόβλημα του εγγύτερου ζεύγους που παρουσιάστηκε στο 6.1.1 σε χρησιμοποιώντας την τεχνική διαίρει και βασίλευε. Ας περιγράψουμε όμως αρχικά την τεχνική αυτή. Η ιδέα της τεχνικής διαίρει και βασίλευε είναι η αναδρομική διάσπαση ενός προβλήματος σε δύο ή περισσότερα υποπροβλήματα (διαίρει) έως ότου φτάσουμε σε απλά υποπροβλήματα που λύνονται απευθείας (βασίλευε). Έπειτα, οι λύσεις στα υποπροβλήματα συνδυάζονται μεταξύ τους, ώστε να δώσουν τη λύση σε ένα μεγαλύτερο πρόβλημα (συνδυασμός). Το τρίτο βήμα προφανώς δεν περιγράφεται από το όνομα αυτής της τεχνικής. Στην δυαδική αναζήτηση για παράδειγμα, η διαίρεση αφορά την μετακίνηση είτε στο αριστερό ή στο δεξιό μισό του πίνακα με βάση την σύγκριση με το μεσαίο στοιχείο του πίνακα. Το βήμα βασίλευε είναι τετριμμένο και αναφέρεται πολύ απλά στην σύγκριση που κάνουμε για να βρούμε το στοιχείο που αναζητούμε, ενώ τέλος το βήμα συνδυάσε είναι επίσης τετριμμένο, αφού δεν απαιτείται συνδυασμός λύσεων. Στον αλγόριθμο γρήγορης ταξινόμησης που θα δούμε στο Κεφάλαιο 8, το βήμα διαίρεσης απαιτεί την διάσπαση του προβλήματος σε δύο (όχι απαραίτητα ίσα υποπροβλήματα) με βάση ένα στοιχείο διαχωρισμού (pivot), το βήμα βασίλευε απλώς ταξινομεί έναν πίνακα δύο στοιχείων με μία σύγκριση και τέλος το βήμα συνδύασε είναι τετριμμένο, αφού τα υποπροβλήματα είναι ήδη ταξινομημένα μεταξύ τους. Από την άλλη πλευρά, ο αλγόριθμος συγχώνευσης έχει ένα τετριμμένο βήμα διαίρεσης, αφού διασπά τον πίνακα πάντα στη μέση, στο βήμα βασίλευε κάνει ότι και ο αλγόριθμος γρήγορης αναζήτησης αλλά η πολυπλοκότητά του βρίσκεται στο βήμα συνδύασε, όπου θα πρέπει να συγχωνεύσει δύο ταξινομημένους πίνακες σε έναν μεγαλύτερο ταξινομημένο πίνακα.
Ας γυρίσουμε όμως πάλι στο πρόβλημα του εγγύτερου ζεύγους σημείων στον δισδιάστατο χώρο. Θέλουμε να εφαρμόσουμε την τεχνική διαίρει και βασίλευε με την ελπίδα ότι θα λύσουμε πιο αποδοτικά το πρόβλημα. Καταρχάς, για το διαίρει βήμα θα ήταν λογικό (διαισθητικό επιχείρημα) να χωρίσουμε τα σημεία ακριβώς στη μέση με βάση μία συντεταγμένη τους. Βεβαίως, η προσπάθεια αυτή μπορεί να αποτύχει και να χρειαστεί να κάνουμε μία άλλη διαίρεση αλλά ένας καλός κανόνας στη σχεδίαση αλγορίθμων είναι η απλότητα. Επομένως, ταξινομούμε τα σημεία ως προς τη συντεταγμένη τους και έπειτα χωρίζουμε το σύνολο των σημείων σε δύο ίσου μεγέθους υποσύνολα και (το πρόβλημα σε δύο υποπροβλήματα) με βάση την κάθετη ευθεία . Οπότε λύνουμε αναδρομικά το πρόβλημα σε κάθε υποσύνολο σημείων. Βρίσκουμε το ελάχιστο σε κάθε υποσύνολο και το επιστρέφουμε στο προηγούμενο βήμα της αναδρομής. Το βήμα βασίλευε μάλλον θα είναι επίσης εύκολο, αφού το μόνο που χρειάζεται να κάνουμε είναι όταν φτάνουμε σε ένα υποπρόβλημα με δύο σημεία απλώς υπολογίζουμε την μεταξύ τους απόσταση και την επιστρέφουμε.
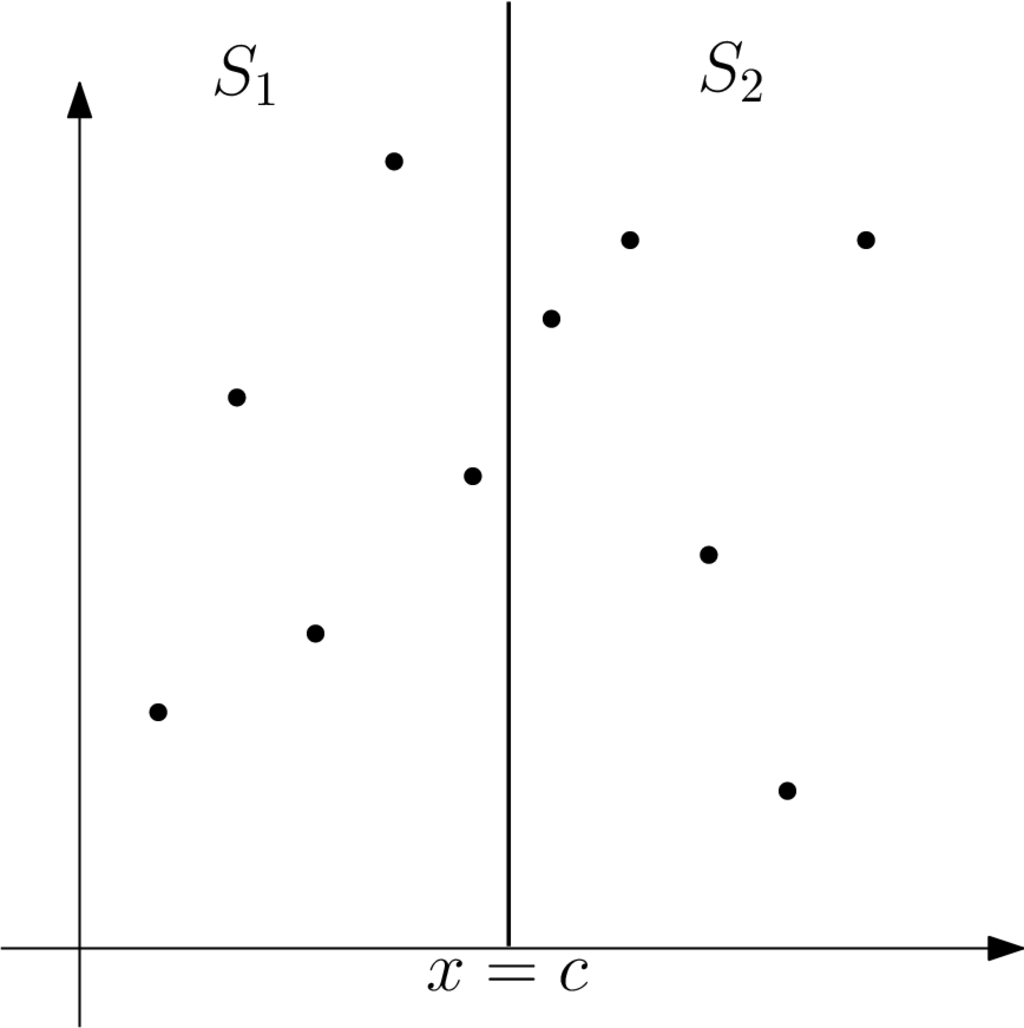
Το πρόβλημα είναι ότι το εγγύτερο ζεύγος δεν είναι απαραίτητο να βρίσκεται σε ένα υποσύνολο αλλά υπάρχει η περίπτωση το ένα σημείο του εγγύτερου ζεύγους σε κάποια αναδρομή να βρίσκεται στο υποσύνολο και το άλλο σημείο στο υποσύνολο (Σχήμα 6.2). Το βήμα συνδύασε είναι υπεύθυνο να δώσει λύση σε αυτό το πρόβλημα. Πώς συνδυάζουμε λοιπόν τις δύο λύσεις από δύο υποπροβλήματα, για να βρούμε τη λύση στο μεγαλύτερο υποπρόβλημα; Η απάντηση είναι ότι ψάχνουμε το ζεύγος με την ελάχιστη απόσταση μεταξύ του ζεύγους ελάχιστης απόστασης (έστω ) από το , του ζεύγους ελάχιστης απόστασης (έστω ) από το και τέλος το ζεύγος ελάχιστης απόστασης μεταξύ όλων των ζευγών που σχηματίζονται, όταν το ένα σημείο είναι στο και το άλλο στο . Προφανώς κάποιος θα απαντήσει ότι το μέγιστο πλήθος αυτών των ζευγών είναι (φανταστείτε ότι στην πρώτη αναδρομή το έχει σημεία και το έχει επίσης σημεία. Επομένως, δεν πετύχαμε κάτι καλύτερο από την εξάντληση. Μία πιο προσεκτική παρατήρηση του προβλήματος, όμως, θα μας δείξει ότι αυτό δεν ισχύει.
Έστω ότι η ελάχιστη απόσταση που αφορά ζεύγη των οποίων τα σημεία ανήκουν εξ ολοκλήρου στο ή στο . Για να βρούμε το ζεύγος σημείων που το ένα ανήκει στο και το άλλο ανήκει στο με την ελάχιστη απόσταση απλώς υπολογίζουμε την απόσταση μεταξύ κάθε σημείου του με σημεία του . Είναι, όμως, απαραίτητο να κάνουμε τον υπολογισμό για όλα τα σημεία του ; Η απάντηση είναι όχι, αφού μπορούμε να εκμεταλλευτούμε το γεγονός ότι ξέρουμε το . Αρκεί, λοιπόν, να υπολογίσουμε τις αποστάσεις μόνο για εκείνα τα σημεία του που ενδεχομένως να είναι σε απόσταση . Επομένως, τα σημεία των και που πρέπει να ελέγξουμε δεν μπορεί να βρίσκονται σε απόσταση μεγαλύτερη από από την ευθεία , αφού τότε η απόστασή τους θα είναι σίγουρα . Αυτό σημαίνει ότι αρκεί να ελέγξουμε τα σημεία που βρίσκονται σε μία λωρίδα που είναι συμμετρική γύρω από την κάθετη ευθεία σε απόσταση από αυτή και προς τις δύο κατευθύνσεις κατά τον άξονα, όπως φαίνεται και στο Σχήμα 6.3(α).
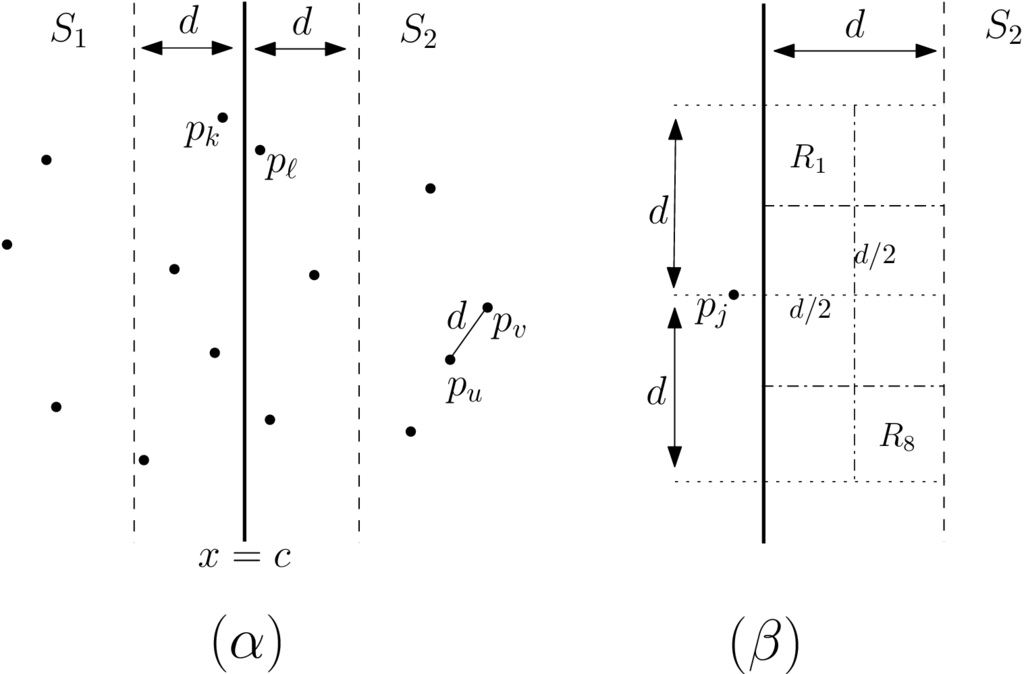
Έστω και τα σημεία εντός της λωρίδας αριστερά και δεξιά αντίστοιχα της κάθετης ευθείας . Για κάθε σημείο θα πρέπει να ελέγξουμε αν υπάρχει κάποιο σημείο του που να έχει μικρότερη απόσταση από . Αυτά τα σημεία του θα πρέπει να έχουν -συνιστώσα στο διάστημα , ώστε να είναι πιθανό να έχουν απόσταση μικρότερη από . Πόσα, όμως, τέτοια σημεία μπορεί να υπάρξουν στο σύνολο ; Η απάντηση είναι ότι δεν μπορεί να υπάρχουν περισσότερα από τέτοια σημεία, όπως φαίνεται και γεωμετρικά στο Σχήμα 6.3(β) μιας και αυτά θα πρέπει να απέχουν αναγκαστικά μεταξύ τους τουλάχιστον . Αυτό σημαίνει ότι για κάθε σημείο του θα πρέπει να ελέγξουμε σημεία από το . Αυτό σημαίνει ότι στη χειρότερη περίπτωση το κόστος (πλήθος υπολογισμών αποστάσεων) θα είναι για το βήμα συνδυάσε και όχι όπως υποθέσαμε πριν.
Για να ολοκληρώσουμε, θα πρέπει τα σημεία του και να είναι ταξινομημένα και ως προς την -συνιστώσα. Προφανώς, θα πρέπει να υπάρχουν δύο αντίγραφα από κάθε σημείο (ή δύο αντίγραφα αναφορών - identifier - σε κάθε σημείο), έτσι ώστε να έχουμε σε έναν πίνακα τα σημεία ταξινομημένα ως προς και σε άλλο πίνακα τα σημεία ταξινομημένα ως προς . Σαρώνουμε τα σημεία του ταξινομημένα ως προς και κατασκευάζουμε ένα άλλο πίνακα με τα σημεία του που βρίσκονται σε απόσταση το πολύ από την ευθεία ταξινομημένα ως προς (το σύνολο ). Αυτό μπορεί να γίνει σε χρόνο με μία απλή σάρωση. Το ίδιο ακριβώς κάνουμε και για το σύνολο . Έπειτα σαρώνουμε τα σημεία του και για κάθε τέτοιο ελέγχουμε το πολύ σημεία από το . Προσέξτε ότι τα σημεία του είναι επίσης ταξινομημένα ως προς και, άρα, φτάνει να ελέγξουμε το πολύ σημεία πριν την αντίστοιχη συνιστώσα και μετά. Τέλος, μπορούμε να φτιάξουμε την ταξινομημένη ακολουθία ως προς την συνιστώσα του συνόλου κάνοντας ένα βήμα συγχώνευσης των δύο ταξινομημένων ακολουθιών σε γραμμικό χρόνο.
Συνολικά χρειαζόμαστε χρόνο για να εκτελέσουμε αυτή τη διαδικασία. Επομένως, ο συνολικός χρόνος για αυτό τον αλγόριθμο με είσοδο σημείων δίνεται από την εξής αναδρομική εξίσωση:
της οποίας η λύση από το βασικό θεώρημα είναι . Αυτός είναι και ο συνολικός χρόνος του αλγορίθμου, αφού για την αρχική ταξινόμηση απαιτείται χρόνο. Όσον αφορά την ορθότητα του αλγορίθμου, ο αλγόριθμος υπολογίζει σωστά το εγγύτερο ζεύγος, αφού σε κάθε αναδρομική κλήση ελέγχει όλες τις δυνατές περιπτώσεις για την εύρεση ενός εγγύτερου ζεύγους. Πράγματι, όλα τα ζεύγη εντός του και έχουν υπολογισθεί αναδρομικά, ενώ για τα ζεύγη μεταξύ σημείων των δύο συνόλων, σωστά ο αλγόριθμος υπολογίζει τις αποστάσεις μόνο των ζευγών εκείνων που ενδεχομένως να έχουν απόσταση μικρότερη από .
6.1.4 Δυναμικός Προγραμματισμός
Ο δυναμικός προγραμματισμός είναι μία εξαιρετικά ισχυρή τεχνική για εύρεση βέλτιστης λύσης σε διάφορα προβλήματα. Για να εφαρμοσθεί θα πρέπει να ισχύει η αρχή της βελτιστότητας η οποία αναφέρει ότι η βέλτιστη λύση σε ένα πρόβλημα εμπεριέχει βέλτιστες λύσεις σε όλα τα σχετικά υποπροβλήματα. Αυτή την ιδιότητα απαιτούσαμε επίσης και στην άπληστη μέθοδο, μόνο που αυτή απαιτούσε και την επιπλέον ιδιότητα, δηλαδή μία καθολικά βέλτιστη λύση να μπορεί να κατασκευασθεί κάνοντας τοπικά βέλτιστες επιλογές, που ως ιδιότητα είναι πολύ ισχυρή και μας δείχνει ότι το πρόβλημα έχει μία εξαιρετικά καλή εσωτερική δομή.
Ο δυναμικός προγραμματισμός δίνει εξαιρετικά αποτελέσματα, όταν οι λύσεις των ίδιων υποπροβλημάτων απαιτούνται πολλές φορές για την επίλυση του μεγαλύτερου προβλήματος. Χρησιμοποιεί την τεχνική της απομνημόνευσης (memoization) - απλώς αποθηκεύουμε τα ενδιάμεσα αποτελέσματα. Ένα πολύ καλό παράδειγμα αυτής της τεχνικής είναι ο υπολογισμός μέσω της αναδρομικής ενός αριθμού Fibonacci. Υπενθυμίζουμε ότι η αναδρομική εξίσωση που παράγει τους αριθμούς Fibonacci είναι η . Αν πάμε να υπολογίσουμε απευθείας το με μία απλή αναδρομή, υλοποιώντας στην ουσία την παραπάνω αναδρομική εξίσωση, τότε το πλήθος των αναδρομικών κλήσεων θα είναι εκθετικά μεγάλο ( για την ακρίβεια, όπου είναι ο χρυσός λόγος). Στο Σχήμα 6.4 φαίνεται ο υπολογισμός του . Όμως, είναι εύκολο να παρατηρήσουμε ότι πολλές φορές υπολογίζουμε τον ίδιο ενδιάμεσο Fibonacci αριθμό. Αν τον υπολογίσουμε μία φορά και τον αποθηκεύσουμε, τότε κάθε φορά που θα αναζητάμε το θα το έχουμε έτοιμο και δεν θα χρειαστεί να το επαναϋπολογίζουμε. Σε αυτή την περίπτωση η πολυπλοκότητα γίνεται (στην πραγματικότητα και αυτή η πολυπλοκότητα είναι ψευδοπολυωνυμική).
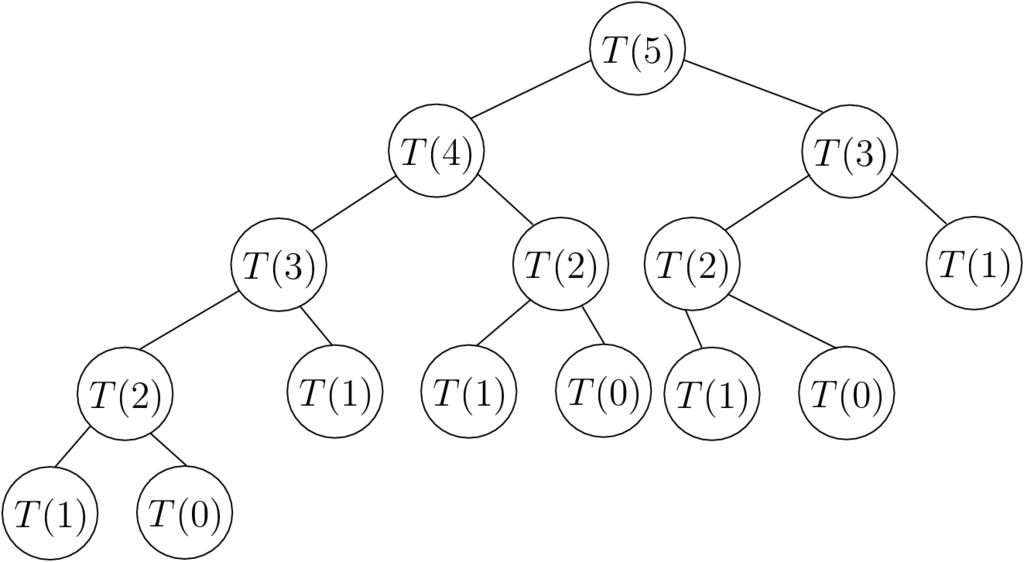
Υπάρχουν δύο τρόποι να εκφράσουμε το δυναμικό πρόγραμμα, αναδρομικά ή επαναληπτικά με πίνακα. Στην ουσία και οι δύο τρόποι είναι ακριβώς ίδιοι, αν και ο δεύτερος προτιμάται μιας και δεν έχει αναδρομή. Ας επιστρέψουμε στο πρόβλημα των ρέστων για το οποίο θα βρούμε έναν αλγόριθμο βασισμένο σε δυναμικό προγραμματισμό που να είναι πάντα βέλτιστος. Έστω λοιπόν το σύνολο των νομισμάτων και το ποσό . Έστω ότι η βέλτιστη λύση ως προς το πλήθος των νομισμάτων για το ποσό είναι . Τότε υπάρχουν οι εξής περιπτώσεις συνολικά: να χρησιμοποιηθεί το νόμισμα σε συνδυασμό με τη την βέλτιστη λύση για το ποσό που απομένει, να χρησιμοποιηθεί το νόμισμα σε συνδυασμό με τη την βέλτιστη λύση για το ποσό που απομένει κοκ. Η διαδικασία αυτή συνεχίζει αναδρομικά μέχρι να φτάσουμε σε μηδενικό ποσό (η τερματική συνθήκη της αναδρομής). Όπως είπαμε παραπάνω είδαμε το ως μία αναδρομική διαδικασία αλλά θα μπορούσαμε να την δούμε και ως έναν πίνακα που γεμίζει με επαναληπτικό τρόπο. Και οι δύο τρόποι όπως είπαμε παραπάνω είναι ίδιοι. Άρα ποιο είναι το δυναμικό πρόγραμμα, δηλαδή η αναδρομική/επαναληπτική διαδικασία;
Πώς θα υλοποιούνταν αυτό σε έναν πίνακα; Έστω ο πίνακας , θέσεων. Αρχικοποιούμε τη θέση με την τιμή . Όπως ίσως καταλάβατε, οι θέσεις του πίνακα αντιστοιχούν σε ποσά και ο στόχος είναι να υπολογίσουμε το , το οποίο θα περιέχει το ελάχιστο πλήθος νομισμάτων για το ποσό . Η θέση υπολογίζεται από τον παραπάνω τύπο με δεδομένο ότι το είναι υπολογισμένο. Γενικά, το υπολογίζεται από τον παραπάνω τύπο με βάση τις ήδη υπολογισμένες τιμές (απομνημόνευση) στις θέσεις . Αφού σε κάθε θέση του πίνακα θα πρέπει να πάρουμε το ελάχιστο από προηγούμενες θέσεις του πίνακα (το πολύ), η πολυπλοκότητα του αλγόριθμου είναι .
Μία στιγμή όμως!!! Υπολογίσαμε το ελάχιστο πλήθος των νομισμάτων αλλά όχι ποια θα είναι αυτά τα νομίσματα. Μπορούμε να το κάνουμε αυτό; Η απάντηση είναι ναι. Πιο συγκεκριμένα, ξεκινάμε από τη θέση και ελέγχουμε όλες τις θέσεις από τις οποίες μπορούμε να φτάσουμε εκεί για κάθε νόμισμα. Αυτό σημαίνει ότι ελέγχουμε τις θέσεις και επιλέγουμε να συνεχίσουμε από τη θέση που έχει την ελάχιστη τιμή, έστω την θέση . Αυτό σημαίνει ότι το νόμισμα με τιμή έχει χρησιμοποιηθεί στη βέλτιστη λύση. Συνεχίζουμε με τον ίδιο τρόπο από την θέση μέχρι να φτάσουμε στη θέση . Στην ουσία εκτελούμε την ίδια διαδικασία με τον υπολογισμό του αλλά ανάποδα. Αυτή η διαδικασία θα μπορούσε να ολοκληρωθεί πιο γρήγορα αν προσθέταμε λίγη πληροφορία επιπλέον. Καθώς θα υπολογίζουμε τον πίνακα θα υπολογίσουμε και έναν επιπλέον πίνακα με τη βέλτιστη επιλογή νομίσματος που κάναμε σε κάθε βήμα. Έτσι, με τους πίνακες και θα μπορούσαμε να βρούμε το σύνολο των νομισμάτων που χρησιμοποιήθηκαν.
6.1.5 Οπισθοδρόμηση
Η οπισθοδρόμηση είναι μία γενική μέθοδος σχεδιασμού αλγορίθμων που επί της ουσίας αποτελεί μία βελτίωση της εξάντλησης. Ως τέτοια πολλές φορές συμπίπτει με την εξάντληση, ενώ άλλες φορές οδηγεί σε πιο αποδοτικές λύσεις. Για να καταλάβουμε καλύτερα τι είναι η οπισθοδρόμηση φανταστείτε το πρόβλημα της εύρεσης της εξόδου από έναν λαβύρινθο. Τι κάνουμε για να βρούμε την έξοδο, ή αλλιώς, ποιος είναι αλγόριθμος για να βρούμε την έξοδο; Ξεκινάμε από την αρχή του λαβύρινθου και αν στο βήμα που κάνουμε βρούμε την έξοδο, τότε σταματάμε (τερματική συνθήκη). Διαφορετικά, από την τρέχουσα θέση κάνουμε ένα βήμα - επιλέγουμε στην ουσία που θα πάμε - και αναδρομικά συνεχίζουμε. Αν βρεθούμε σε αδιέξοδο επιστρέφουμε πίσω (αποτυγχάνουμε), ενώ αν όλα τα βήματα αποτύχουν, τότε επιστρέφουμε την απάντηση ότι ο λαβύρινθος δεν έχει έξοδο. Στην ουσία εφαρμόζουμε εξάντληση μόνο που δείχνουμε ξεκάθαρα το βήμα οπισθοδρόμησης (πήγαινε πίσω στην αναδρομή στην προηγούμενη επιλογή που έκανες και κάνε μία καινούργια). Αυτό το σκαρίφημα αλγορίθμου χρησιμοποιεί αναδρομή αλλά θα μπορούσαμε να το κάνουμε και με επανάληψη - άλλωστε κάθε αναδρομική διαδικασία μπορεί να εξομοιωθεί από μία επανάληψη με χρήση μίας στοίβας!
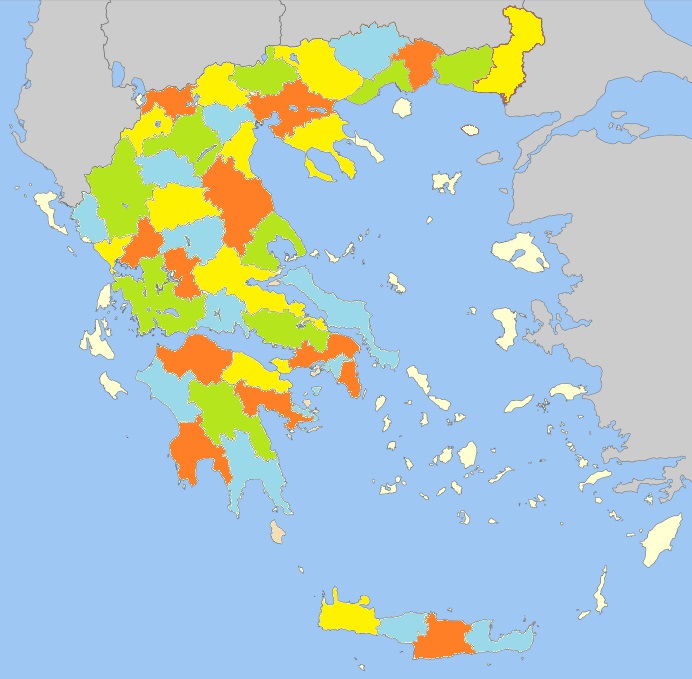
Ας δούμε λίγο πιο αναλυτικά όμως ένα άλλο πρόβλημα: το πρόβλημα του χρωματισμού ενός χάρτη με χρώματα. Έστω ότι ο χάρτης είναι μία επίπεδη υποδιαίρεση του δισδιάστατου χώρου - ναι, σαν έναν κλασσικό χάρτη νομών με τα σύνορά τους (Σχήμα 6.5) Η ερώτηση είναι να βρεθεί ένας χρωματισμός των χωρών με χρώματα, ώστε ανά δύο όλες οι χώρες που συνορεύουν να έχουν διαφορετικό χρώμα. Καταρχάς, υπάρχει τέτοιος χρωματισμός; Η απάντηση είναι ότι πάντα υπάρχει ένας τέτοιος χρωματισμός [7] και η απόδειξη για αυτό είναι μία από τις πρώτες αποδείξεις που έκαναν χρήση υπολογιστή λόγω των πολλών περιπτώσεων που έπρεπε να ελεγχθούν.
Στην εξάντληση η λύση θα ήταν να κατασκευάζουμε όλους τους δυνατούς χρωματισμούς και για κάθε τέτοιον χρωματισμό να ελέγχουμε αν υπάρχουν γειτονικές χώρες με ίδιο χρώμα, οπότε και θα συνεχίζαμε στην επόμενη λύση μέχρι να βρούμε έναν τέτοιο χρωματισμό. Στην ουσία θα μετράγαμε από το έως το χρησιμοποιώντας έναν μετρητή στο τετραδικό σύστημα αρίθμησης με ψηφία. Για παράδειγμα, το θα αντιστοιχούσε στο κόκκινο () στην πρώτη χώρα, στο πράσινο () στη δεύτερη και τρίτη χώρα, στο άσπρο () στην τέταρτη χώρα, στο κόκκινο στην πέμπτη χώρα, στο μαύρο () στην έκτη χώρα, κ.ο.κ.
Όταν χρησιμοποιήσουμε οπισθοδρόμηση όμως, τότε μπορούμε να κάνουμε κάτι αρκετά πιο έξυπνο, αν και στη χειρότερη περίπτωση μπορεί να είναι σχεδόν ίδιο με την εξάντληση. Η ιδέα είναι ότι αναδρομικά (ή και επαναληπτικά) θα επεκτείνουμε μία λύση και αν αυτή κάποια στιγμή οδηγήσει σε αποτυχία, τότε θα επιστρέψουμε στην αναδρομή στην προηγούμενη επιλογή (οπισθοδρόμηση). Ο αλγόριθμος, λοιπόν, θα έχει ως τερματική συνθήκη τον επιτυχή χρωματισμό όλων των χωρών. Για κάθε χρώμα και για τη χώρα , αν η χώρα δεν είναι γειτονική σε χώρα με το χρώμα , τότε τη χρωματίζουμε με αυτό το χρώμα και αναδρομικά χρωματίζουμε την χώρα , διαφορετικά αποτυγχάνουμε και επιστρέφουμε (στο προηγούμενο επίπεδο της αναδρομής).
Μπορούμε να δούμε την οπισθοδρόμηση ως έναν τρόπο να εξερευνούμε το χώρο των λύσεων μέχρι να βρούμε μία λύση που να έχει την επιθυμητή ιδιότητα. Η εξερεύνηση αυτή γίνεται με έναν δομημένο τρόπο, ως δένδρο. Αυτό το δένδρο το ονομάζουμε δένδρο χώρου καταστάσεων (state space tree). Η ρίζα του δένδρου αποτελεί την αρχική κατάσταση, ενώ οι κόμβοι του αντιστοιχούν σε επιλογές που γίνονται για τη λύση. Κάθε φύλλο του δένδρου αντιστοιχεί σε μία λύση. Κάποιοι κόμβοι μπορεί να οδηγούν σε επιθυμητές λύσεις, ενώ κάποιοι άλλοι να μην οδηγούν σε επιθυμητές λύσεις, με την έννοια ότι δεν υπάρχει φύλλο στο υποδένδρο τους που να έχει την επιθυμητή ιδιότητα, δηλαδή να αντιστοιχεί σε μία κατανομή των χρωμάτων σε χώρες, ώστε όλες ανά δύο να έχουν διαφορετικά χρώματα. Η εξερεύνηση σε αυτό το δένδρο γίνεται με μία διαπέραση κατά βάθος, σταματώντας όμως σε κόμβους που εγγυημένα δεν οδηγούν σε επιθυμητή λύση (μιας και η επιλογή που κάνουμε σε αυτούς εγγυημένα δεν είναι καλή). Σε αυτή την περίπτωση ο αλγόριθμος οπισθοδρομεί στον πατέρα του μέσα στο δένδρο.

Στο Σχήμα 6.6 φαίνεται ένα τέτοιο δένδρο καταστάσεων για το πρόβλημα του χρωματισμού. Με δεδομένο ότι αν έχουμε έναν έγκυρο χρωματισμό, τότε η αλλαγή των χρωμάτων που χρησιμοποιούμε δεν μεταβάλλει την εγκυρότητα της λύσης, μπορούμε να θεωρήσουμε ότι η ρίζα του δένδρου καταστάσεων αντιστοιχεί στο πράσινο χρώμα του νομού Αρκαδίας. Για να το εξηγήσουμε, αν το πράσινο το αλλάξτε με κίτρινο και το κίτρινο με πράσινο, ο χρωματισμός του Σχήματος 6.5 παραμένει έγκυρος. Η επόμενη επιλογή του αλγορίθμου αφορά την Αχαΐα, όπου ο αλγόριθμος δίνει το χρώμα πράσινο. Με αυτή την επιλογή όμως παραβιάζεται η εγκυρότητα της λύσης και, άρα, ο αλγόριθμος δεν συνεχίζει αναδρομικά σε αυτό τον κόμβο αλλά κάνει μία άλλη επιλογή, δηλαδή επιλέγει την Αχαΐα να την χρωματίσει με πορτοκαλί. Για αυτό ακριβώς το λόγο έχουμε διαγράψει τον πράσινο κόμβο της Αχαΐας, οπισθοδρομήσαμε στον πατέρα και έπειτα κάναμε μία καινούργια επιλογή. Με τον ίδιο τρόπο συνεχίζουμε και στην Ηλεία κ.ο.κ.. Προσέξτε, ότι με αυτή την οπισθοδρόμηση ο αλγόριθμος γλυτώνει αρκετά βήματα υπολογισμού σε σχέση με την μέθοδο της εξάντλησης. Παρ’ όλ’αυτά, αυτό δεν είναι πάντοτε αληθές και μπορεί η μέθοδος της οπισθοδρόμησης να εκφυλίζεται στη μέθοδο της εξάντλησης. Όσον αφορά την απόδοση, ασυμπτωτικά οι δύο λύσεις δεν διαφέρουν για το πρόβλημα του χρωματισμού χάρτη με χρώματα αλλά σίγουρα στην πράξη θα ήταν πιο γρήγορη η οπισθοδρόμηση.
6.1.6 Διακλάδωση και Περιορισμός
Η μέθοδος διακλάδωσης και περιορισμού χρησιμοποιείται συνήθως για τη λύση προβλημάτων βελτιστοποίησης, προβλημάτων δηλαδή που ο στόχος είναι να ελαχιστοποιήσουμε ή να μεγιστοποιήσουμε μία ποσότητα. Ένας τέτοιος αλγόριθμος εξερευνά το χώρο των λύσεων ενός δοθέντος προβλήματος, για να ανακαλύψει τη καλύτερη λύση. Η εξερεύνηση του τεράστιου συνήθως αυτού χώρου επιταχύνεται κάνοντας χρήση της τρέχουσας καλύτερης λύσης που έχει βρεθεί καθώς και κάποιων ορίων για τη συνάρτηση που θέλουμε να βελτιστοποιήσουμε, ώστε να μην χρειαστεί να ψάξουμε όλο το χώρο. Αντίστοιχα με την τεχνική της οπισθοδρόμησης αναπαριστούμε το χώρο με ένα δένδρο καταστάσεων, ενώ ο αλγόριθμος διαπερνά αυτό το δένδρο. Μία από τις διαφορές είναι ότι η διαπέραση δεν είναι μονο κατά βάθος, αλλά μπορεί να είναι κατά πλάτος ή με κάποιο άλλο κριτήριο (ενδεχομένως αυτό το κριτήριο να έχει σχέση με τα όρια).
Γενικά ένας τέτοιος αλγόριθμος περιέχει τρία θεμελιώδη συστατικά: μία διαδικασία διακλάδωσης, μία διαδικασία περιορισμού και έναν κανόνα επιλογής. Η διαδικασία διακλάδωσης αναδρομικά επεκτείνει ένα υποπρόβλημα σε υποπροβλήματα, έτσι ώστε η βέλτιστη λύση να μπορεί να βρεθεί λύνοντας καθένα από αυτά τα υποπροβλήματά του. Η διαδικασία περιορισμού υπολογίζει ένα κάτω φράγμα για το κόστος της βέλτιστης λύσης για κάθε υποπρόβλημα που επεκτείνεται και το χρησιμοποιεί για να αποφασίσει αν είναι απαραίτητη η περαιτέρω εξερεύνηση ενός υποπροβλήματος. Αυτές οι δύο διαδικασίες εξαρτώνται από το πρόβλημα που αντιμετωπίζουμε. Ο κανόνας επιλογής καθορίζει τη σειρά με την οποία θα γίνει η διακλάδωση στα υποπροβλήματα. Συνήθως δεν εξαρτάται από το πρόβλημα και μπορεί να περιλαμβάνει κανόνες όπως η κατά βάθος διαπέραση, κατά πλάτος διαπέραση ή ακόμα και τυχαιοποιημένους κανόνες.
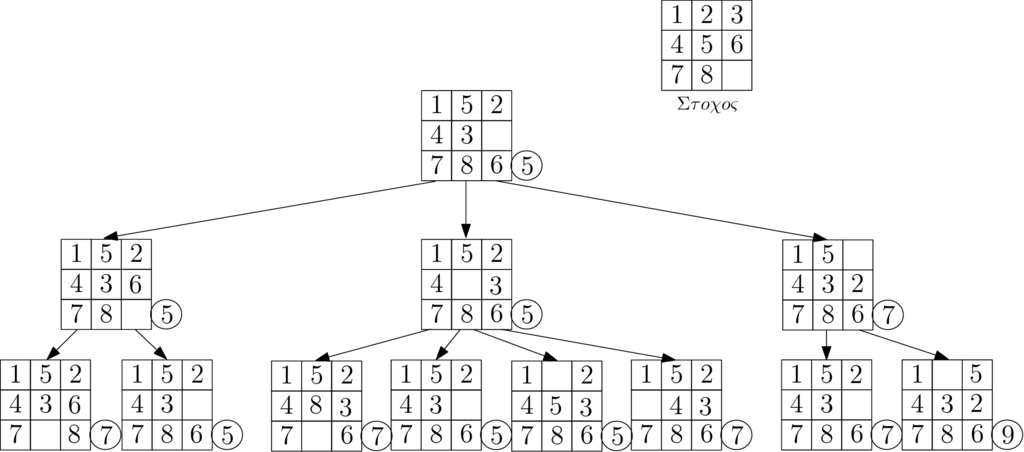
Ας εφαρμόσουμε αυτή την τεχνική σε ένα απλό πρόβλημα, σε αυτό του γρίφου των αριθμών (Σχήμα 6.7). Ο γρίφος των αριθμών αποτελείται από κουτιά αριθμημένα από το έως το που έχουν τοποθετηθεί σε ένα πλαίσιο . Οι οκτώ θέσεις του πλαισίου περιέχουν ακριβώς από ένα κουτί, ενώ μία θέση είναι κενή. Ο στόχος του παιχνιδιού είναι να γεμίζουμε το κενό με γειτονικά (κάθετα ή οριζόντια) κουτιά, έτσι ώστε στο τέλος οι αριθμοί να είναι σε σειρά ανά γραμμή. Αυτό θέλουμε να το πετύχουμε ελαχιστοποιώντας το πλήθος των κινήσεων στο πλαίσιο.
Αφού θέλουμε να ελαχιστοποιήσουμε μία ποσότητα, αναζητούμε ένα κάτω φράγμα στις κινήσεις που πρέπει να γίνουν σε κάθε στιγμιότυπο, ώστε να φτάσουμε σε λύση. Αυτό σημαίνει ότι αν έχουμε μία λύση που έχει πλήθος κινήσεων αυστηρά μικρότερο από το κάτω φράγμα που έχει ένας κόμβος, τότε είναι ανούσιο να συνεχίσουμε το ψάξιμο στο υποδένδρο του κόμβου αυτού μιας και αποκλείεται να βρούμε μία καλύτερη λύση. Ποιο είναι όμως το κάτω φράγμα που θα επιλέξουμε; Σε αυτό το πρόβλημα ένα κάτω φράγμα ως προς τις κινήσεις που πρέπει να κάνουμε για να φτάσουμε από ένα αυθαίρετο στιγμιότυπο στο στόχο είναι ίσο με το άθροισμα των κινήσεων που έχουμε κάνει για να φτάσουμε σε αυτό το κόμβο συν το άθροισμα των αποστάσεων Manhattan ( απόσταση) από τις τρέχουσες θέσεις προς τις θέσεις των αριθμών στο στόχο. Για παράδειγμα, στη ρίζα του δένδρου στο Σχήμα 6.7 το κάτω φράγμα είναι , αφού το χρειάζεται μία κίνηση προς τα κάτω, ώστε να βρεθεί στην τελική του θέση, το χρειάζεται μία κίνηση προς τα αριστερά, το μία κίνηση προς τα δεξιά και μία προς τα πάνω (ή πάνω και δεξιά) και τέλος το χρειάζεται μία κίνηση, για να βρεθεί στη σωστή του θέση. Όλοι οι υπόλοιποι αριθμοί βρίσκονται στη σωστή τους θέση σε σχέση με τον στόχο. Επομένως, θα χρειαστούν τουλάχιστον κινήσεις για να φτάσουμε στο στόχο. Αυτό βέβαια δεν σημαίνει ότι κινήσεις είναι αρκετές, απλώς δεν υπάρχει ακολουθία κινήσεων με πλήθος κινήσεων μικρότερο του .
Η διαπέραση του δένδρου μπορεί να γίνει κατά βάθος ή κατα πλάτος ελέγχοντας κάθε φορά, αν το κάτω όριο του κόμβου είναι μικρότερο ή ίσο με το τρέχων καλύτερο κόστος. Ένας, όμως, συνήθως καλύτερος τρόπος διαπέρασης με την έννοια ότι φτάνουμε πιο γρήγορα στη λύση είναι να επιλέγουμε πάντα τον κόμβο με το μικρότερο κάτω όριο χωρίς αυτό να σημαίνει ότι δεν υπάρχουν και άλλοι τρόποι διαπέρασης. Ας επιστρέψουμε πάλι στο παράδειγμά μας. Στην αρχή δεν έχουμε κάποια λύση, οπότε θεωρούμε ότι το κόστος της είναι . Ξεκινάμε από τη ρίζα που έχει ελάχιστο κόστος , οπότε αυτό είναι και το νέο ελάχιστο. Από τα τρία παιδιά του, που αντιστοιχούν στις τρεις δυνατές κινήσεις, θα προτιμήσουμε να επιλέξουμε την αριστερή ή την μεσαία μιας και αυτές έχουν κάτω φράγμα το επίσης, σε αντίθεση με το δεξιό παιδί που έχει κάτω φράγμα . Συνεχίζοντας από το αριστερό επιλέγουμε το δεξιό παιδί και συνεχίζουμε αναδρομικά μέχρι να φτάσουμε σε μία λύση. Έπειτα επιστρέφουμε από την αναδρομή χωρίς να εξερευνούμε τα υποδένδρα των οποίων το κάτω φράγμα είναι μεγαλύτερο από τη λύση που βρήκαμε.
6.2 Μέγιστο Άθροισμα Υποακολουθίας
Δίνεται ένας πίνακας με ακέραιους αριθμούς και ζητείται να βρεθεί ο υποπίνακας εκείνος, του οποίου το άθροισμα των τιμών των στοιχείων είναι μέγιστο σε σχέση με κάθε άλλο υποπίνακα που μπορεί να θεωρηθεί. Για παράδειγμα, στον Πίνακα 6.1 το μέγιστο άθροισμα των τιμών των στοιχείων δίνεται από τον υποπίνακα A[3..5] και είναι ίσο με 19.
| 6 | -8 | 7 | 10 | 2 | -4 | 3 |
Στο πρόβλημα αυτό υπάρχουν δύο προφανείς λύσεις. Αν ο πίνακας περιέχει μόνο θετικούς αριθμούς, τότε η λύση είναι ολόκληρος ο πίνακας. Όταν ο πίνακας περιέχει μόνο αρνητικούς αριθμούς τότε η λύση είναι ένας υποπίνακας με 0 στοιχεία. Σε κάθε άλλη περίπτωση, το πρόβλημα θέλει ιδιαίτερη προσοχή. Στη συνέχεια, θα εξετάσουμε τέσσερις αλγορίθμους, όπου διαδοχικά θα βελτιώνουμε την πολυπλοκότητά τους.
Πρώτος Αλγόριθμος (Εξαντλητική Αναζήτηση)
Κατ’ αρχάς παρουσιάζεται η πρώτη μας προσπάθεια: ένας προφανής τρόπος επίλυσης του προβλήματος, όπου εξετάζεται κάθε δυνατή περίπτωση υποπίνακα. Η συνάρτηση max_subseq_sum1 που ακολουθεί, δέχεται τον πίνακα A, που αποτελείται από στοιχεία, και επιστρέφει τη ζητούμενη μέγιστη τιμή. Με left και right συμβολίζονται τα δύο ακραία στοιχεία της υποακολουθίας, που κάθε φορά εξετάζεται. Για κάθε εξεταζόμενη υποακολουθία, το αντίστοιχο άθροισμα των τιμών των στοιχείων της υπολογίζεται με τη βοήθεια της μεταβλητής current_sum που συγκρίνεται με τη μεταβλητή max_sum και την αντικαθιστά αν έχει μεγαλύτερη τιμή.
function max_subseq_sum1;
1. max_sum <-- 0; left <-- 0; right <-- 0;
2. for i <-- 1 to n do
3. for j <-- i to n do
4. current_sum <-- 0;
5. for k <-- i to j do
6. current_sum <-- current_sum+A[k];
7. if (current_sum>max_sum) then
8. max_sum <-- current_sum;
9. left <-- i; right <-- j
10. return max_sum
Η συνάρτηση αυτή αποτελείται από τρεις φωλιασμένες εντολές for. Η εύρεση της πολυπλoκότητας αναδεικνύεται εύκολα, όπως φαίνεται στη συνέχεια, θεωρώντας ως βαρόμετρο την εντολή 6 (με μοναδιαίο κόστος), που βρίσκεται στο εσωτερικότερο σημείο των βρόχων.
Έτσι, προκύπτει ότι η πολυπλοκότητα αυτού του αλγορίθμου είναι Θ().
Δεύτερος Αλγόριθμος (Εξαντλητική Αναζήτηση)
Παρατηρώντας τον προηγούμενο αλγόριθμο εύκολα βγαίνει το συμπέρασμα ότι γίνονται πολλοί περιττοί υπολογισμοί. Έτσι, προκειμένου να βελτιωθεί η πολυπλοκότητα του αλγορίθμου αυτού, μπορεί να παραληφθεί η μία από τις τρεις φωλιασμένες εντολές for. Αυτό προκύπτει από την παρατήρηση ότι το άθροισμα των τιμών των στοιχείων του υποπίνακα A(left..right) είναι ίσο με το άθροισμα των τιμών των στοιχείων του υποπίνακα A(left..right-1) και του στοιχείου A(right), οπότε κατά τον υπολογισμό του A(left..right) υπολογίζεται και πάλι το άθροισμα των τιμών των στοιχείων A(left..right-1). Αν γίνει η αλλαγή αυτή στη συνάρτηση max_subseq_sum1 προκύπτει η συνάρτηση max_subseq_sum2.
function max_subseq_sum2;
1. max_sum <-- 0; left <-- 0; right <-- 0;
2. for i <-- 1 to n do
3. current_sum <-- 0;
4. for j <-- i to n do
5. current_sum <-- current_sum+A[j];
6. if (current_sum>max_sum) then
7. max_sum <-- current_sum;
8. left <-- i; right <-- j
9. return max_sum
Ευκολότερα από την προηγούμενη φορά είναι δυνατόν να αποδειχθεί ότι ο αλγόριθμος έχει τετραγωνική πολυπλοκότητα Θ().
Τρίτος Αλγόριθμος (διαίρει και βασίλευε)
Μία διαφορετική αντιμετώπιση του προβλήματος προκύπτει ακολουθώντας τη στρατηγική Διαίρει και Βασίλευε, δηλαδή διαιρώντας τον πίνακα σε δύο υποπίνακες (σχεδόν) ίσου μήκους. Για τα υποδιανύσματα αυτά υπολογίζονται αναδρομικά οι ακολουθίες μέγιστου αθροίσματος, διαιρώντας τα σε επί μέρους υποδιανύσματα, αν και όσο χρειασθεί. Έτσι, διακρίνουμε τρεις περιπτώσεις: η υποακολουθία του μέγιστου αθροίσματος είτε περιέχεται στο πρώτο μισό του αρχικού πίνακα, είτε περιέχεται στο δεύτερο μισό, είτε τέλος περιέχεται και στα δύο. Όταν ισχύει η τρίτη περίπτωση, τότε η λύση του προβλήματος βασίζεται στη σκέψη ότι πρέπει να υπολογισθεί αφενός η υποακολουθία με μέγιστο άθροισμα του πρώτου μισού, η οποία περιέχει το τελευταίο στοιχείο του πρώτου υποπίνακα και αφετέρου η υποακολουθία με μέγιστο άθροισμα του δεύτερου μισού, η οποία περιέχει το πρώτο στοιχείο του δεύτερου υποπίνακα. Η λύση του αρχικού προβλήματος είναι εκείνη από τις τρεις υποακολουθίες που έχει το μέγιστο άθροισμα των τιμών των στοιχείων της.
Για παράδειγμα, αν ο πίνακας Α έχει την πρώτη μορφή του Πίνακα 6.2, τότε διαιρείται στο μέσο και προκύπτει η δεύτερη μορφή του σχήματος. Με βάση αυτή τη θεώρηση υπολογίζεται η υποακολουθία μέγιστου αθροίσματος του πρώτου μισού (είναι ο υποπίνακας A(1..2)=(3,3) με άθροισμα 6), η υποακολουθία του δεύτερου μισού (είναι ο υποπίνακας A(7)=(7) με ένα μόνο στοιχείο) και η υποακολουθία που περιέχει το τελευταίο στοιχείο του πρώτου μισού και το πρώτο του δεύτερου μισού (είναι ο υποπίνακας A(4..7)=(1,4,-4,7) με άθροισμα 8). Επομένως, η υποακολουθία με μέγιστο άθροισμα είναι ο υποπίνακας A(4...7) με άθροισμα των τιμών των στοιχείων ίσο με 8.
| 3 | 3 | -7 | 1 | 4 | -4 | 7 | -6 | 2 | 1 |
| 3 | 3 | -7 | 1 | 4 | -4 | 7 | -6 | 2 | 1 |
Η αναδρομική συνάρτηση max_subseq_sum3 υπολογίζει το μέγιστο άθροισμα των τιμών των στοιχείων μεταξύ όλων των υποακολουθιών του πίνακα A, διαιρώντας τον πίνακα σε επιμέρους τμήματα. Αυτό είναι το σκέλος Διαίρει. Η βασική συνθήκη (base case) θεωρεί την υποακολουθία με ένα μόνο στοιχείο, όπου αν το στοιχείο αυτό έχει τιμή θετική, τότε το άθροισμα ισούται με την τιμή αυτή, αλλιώς το άθροισμα ισούται με μηδέν. Με άλλα λόγια, στο σημείο αυτό υλοποιείται το σκέλος Βασίλευε της γενικής μεθόδου.
function max_subseq_sum3(left,right);
1. if left=right then
2. if A[left]>0 then return A[left]
3. else return 0;
4. else
5. center <-- (left+right)/2;
6. max_lsum <-- max_subseq_sum3(left,center);
7. max_rsum <-- max_subseq_sum3(center+1,right);
8. max_lborder_sum <-- 0; lborder_sum <-- 0;
9. for i <-- center downto left do
10. lborder_sum <-- lborder_sum+A[i];
11. if (lborder_sum>max_lborder_sum) then
12. max_lborder_sum <-- lborder_sum
13. max_rborder_sum <-- 0; rborder_sum <-- 0;
14. for i <-- center+1 to right do
15. rborder_sum <-- rborder_sum+A[i];
16. if (rborder_sum>max_rborder_sum) then
17. max_rborder_sum <-- rborder_sum
18. temp <-- max_lborder_sum+max_rborder_sum;
19. return max(max_lsum,max_rsum,temp)
Οι χρησιμοποιούμενες μεταβλητές είναι ακέραιες και έχουν το εξής νόημα. Οι μεταβλητές max_lsum και max_rsum εξυπηρετούν τις δύο πρώτες περιπτώσεις που αναφέρθηκαν και δίνουν το μέγιστο άθροισμα για το αριστερό και δεξιό υποπίνακα, αντίστοιχα. Οι υπόλοιπες μεταβλητές αφορούν στην τρίτη περίπτωση. Οι μεταβλητές lborder_sum και rborder_sum δίνουν το κάθε φορά υπολογιζόμενο άθροισμα στα αριστερά και δεξιά του center, ενώ στις max_lborder_sum και max_rborder_sum αποθηκεύεται το μέχρι στιγμής μέγιστο άθροισμα για το αριστερό και δεξιό υποπίνακα αντίστοιχα, τα οποία αργότερα θα προστεθούν για να δώσουν το αποτέλεσμα της τρίτης περίπτωσης. Τέλος, θεωρείται ότι υπάρχει μία συνάρτηση max, που επιστρέφει το μεγαλύτερο από τα στοιχεία που είναι τα ορίσματά της.
Η πολυπλοκότητα της μεθόδου μπορεί να προκύψει με βάση την αντίστοιχη αναδρομική εξίσωση. Κατ’αρχάς, αν το μήκος του πίνακα είναι 1, τότε η δραστηριότητα στις εντολές 1-3 αποτιμάται ως σταθερό μοναδιαίο κόστος, δηλαδή . Αν ο πίνακας είναι μεγαλύτερος, τότε θα εκτελεσθούν δύο αναδρομικές κλήσεις, ενώ στις εντολές 9-17 θα εκτελεσθούν δύο απλοί βρόχοι for γραμμικής πολυπλοκότητας. Επομένως, ισχύει:
| (6.1) |
Θεωρώντας ότι για απλοποίηση, έπεται ότι:
Στο συμπέρασμα αυτό καταλήγουμε αν απλώς θεωρήσουμε ότι το βάθος των αναδρομικών κλήσεων είναι Θ(), ενώ κάθε φορά ο πίνακας υφίσταται επεξεργασία της τάξης Θ(). Ακολουθεί ο τελευταίος αλγόριθμος, που είναι ο καλύτερος που μπορούμε να σχεδιάσουμε.
Τέταρτος Αλγόριθμος (βέλτιστος τρόπος)
Τέλος, λοιπόν, μία ακόμη λύση του προβλήματος που διαπραγματευόμαστε, δίνεται από τη συνάρτηση max_subseq_sum4 που φαίνεται στη συνέχεια. Η συνάρτηση αυτή, σαρώνει όλα τα στοιχεία του πίνακα και τα προσθέτει όσο το άθροισμα τους είναι θετικό. Αν κάποια στιγμή η τιμή του αθροίσματος αυτού γίνει αρνητική, τότε μηδενίζεται η τιμή αυτού του αθροίσματος και συνεχίζεται η άθροιση των τιμών των στοιχείων από το επόμενο στοιχείο.
function max_subseq_sum4;
1. i <-- 0; current_sum <-- 0; max_sum <-- 0;
2. left <-- 0; right <-- 0;
3. for j <-- 1 to n do
4. current_sum <-- current_sum+A[j];
5. if (current_sum>max_sum) then
6. max_sum <-- current_sum;
7. left <-- i; right <-- j
8. else
9. if (current_sum<0) then
10. i <-- j+1; current_sum <-- 0
11. return max_sum;
Ο αλγόριθμος αυτός ανήκει στην κατηγορία των λεγόμενων on-line αλγορίθμων. Οι αλγόριθμοι αυτοί επεξεργάζονται τα δεδομένα όπως έρχονται, δηλαδή δεν είναι ανάγκη τα δεδομένα να είναι γνωστά εκ των προτέρων. Επιπλέον, αυτός ο τρόπος επίλυσης παρουσιάζει το σημαντικό πλεονέκτημα ότι σαρώνει μόνο μία φορά τα στοιχεία του πίνακα. Αυτό σημαίνει ότι αν εξετασθεί κάποιο στοιχείο από τον αλγόριθμο, τότε δεν υπάρχει λόγος να παραμένει κάπου αποθηκευμένο γιατί δεν πρόκειται να χρησιμοποιηθεί ξανά. Επίσης, ένα τελικό πλεονέκτημα του αλγορίθμου αυτού είναι ότι σε κάθε χρονική στιγμή, κατά τη διάρκεια της εκτέλεσης του αλγορίθμου, ο αλγόριθμος έχει υπολογίσει το μέγιστο άθροισμα της υποακολουθίας των στοιχείων που έχει εξετάσει. Η ανάλυση αυτού του αλγορίθμου είναι πολύ εύκολη υπόθεση. Καθώς ο κορμός του αλγορίθμου είναι ένας απλός βρόχος for (εντολή 3), έπεται ότι η πολυπλοκότητα είναι γραμμική Θ().
6.3 Τοποθέτηση 8 Βασιλισσών
Το πρόβλημα αυτό είναι ιστορικό και έχει απασχολήσει τους μεγάλους μαθηματικούς (όπως οι Gausss, Nauck, Guenther, Glaisher) πριν από τα μέσα του 19ου αιώνα. Το πρόβλημα ζητά να βρεθούν όλοι οι δυνατοί τρόποι τοποθέτησης 8 βασιλισσών σε μία σκακιέρα διαστάσεων 8x8 με τέτοιο τρόπο, ώστε να μην αλληλο-απειλούνται. Βέβαια, είναι γνωστό στους σκακιστές ότι δύο βασίλισσες αλληλο-απειλούνται, όταν βρίσκονται στην ίδια γραμμή, στην ίδια στήλη ή στην ίδια διαγώνιο. Συνολικά στο πρόβλημα υπάρχουν 92 λύσεις, αλλά πολλές από αυτές θεωρούνται ισοδύναμες καθώς η μία μπορεί να προκύψει από την άλλη με βάση τη συμμετρία ή εκτελώντας περιστροφές κατά 90. Έτσι, από τις 92 λύσεις προκύπτουν μόνο 12 διακριτές. Στο Σχήμα 6.8 παρουσιάζεται μία λύση του προβλήματος.
| Q | |||||||
| Q | |||||||
| Q | |||||||
| Q | |||||||
| Q | |||||||
| Q | |||||||
| Q | |||||||
| Q |
Ένας προφανής τρόπος επίλυσης του προβλήματος είναι να ελεγχθούν εξαντλητικά όλοι οι δυνατοί τρόποι τοποθέτησης των 8 βασιλισσών στις συνολικά 8x8=64 θέσεις της σκακιέρας. Όμως, ο αριθμός των δυνατών αυτών τοποθετήσεων είναι τεράστιος, καθώς ισούται με το συνδυασμό των 64 θέσεων ανά 8. Άρα, σύμφωνα με τον τρόπο αυτό πρέπει να ελεγχθούν 4.426.165.368 διαφορετικοί τρόποι τοποθέτησης. Μεταξύ αυτών των τρόπων συμπεριλαμβάνονται περιπτώσεις όπου σε μία γραμμή ή σε μία στήλη ή σε μία διαγώνιο μπορεί να τοποθετηθούν όχι μόνο δύο βασίλισσες, αλλά ακόμη περισσότερες, όπως τρεις, τέσσερις, κλπ μέχρι και οκτώ βασίλισσες. Προφανώς ο τρόπος αυτός δεν είναι αποδοτικός και γι’αυτό δεν εξετάζεται στη συνέχεια.
Πρώτος Αλγόριθμος (Εξαντλητική Αναζήτηση)
Μία πρώτη βελτίωση σε σχέση με την προηγούμενη προφανή αλλά μη πρακτική μέθοδο, είναι να θεωρηθεί ότι δεν μπορούν να τοποθετηθούν περισσότερες από μία βασίλισσες στη ίδια γραμμή. Η νέα μέθοδος οδηγεί σε σημαντική βελτίωση καθώς το πλήθος των δυνατών διαφορετικών καταστάσεων μειώνεται σε =16.777.216. Ο αριθμός αυτός προκύπτει λαμβάνοντας υπ’όψιν ότι κάθε βασίλισσα μπορεί να καταλάβει 1 θέση μεταξύ 8 υποψηφίων θέσεων, ενώ η τοποθέτηση μίας βασίλισσας στην αντίστοιχη γραμμή μπορεί, κατ’ αρχάς να θεωρηθεί ανεξάρτητο γεγονός από τις τοποθετήσεις των άλλων βασιλισσών.
Οι βασίλισσες αριθμούνται από 1 ως 8, όπως επίσης οι στήλες και οι γραμμές της σκακιέρας. Έστω ότι η -οστή βασίλισσα τοποθετείται στην -οστή γραμμή και στη στήλη που συμβολίζεται με (όπου ). Άρα, λύσεις του προβλήματος αποτελούν τα διανύσματα , με τέτοιες τιμές των , έτσι ώστε να μην υπάρχουν δύο οποιεσδήποτε βασίλισσες που να βρίσκονται στην ίδια στήλη ή στην ίδια διαγώνιο. Συνεπώς, δεδομένης μίας τοποθέτησης για κάθε ζεύγος βασιλισσών πρέπει να γίνουν δύο έλεγχοι: (α) για το αν βρίσκονται στην ίδια στήλη και (β) για το αν βρίσκονται στην ίδια διαγώνιο. Ο έλεγχος για να διαπιστώσουμε αν δύο βασίλισσες βρίσκονται στην ίδια στήλη είναι εύκολος. Δηλαδή, αν για την -οστή και την -οστή βασίλισσα ισχύει (όπου ), τότε είναι προφανές ότι οι βασίλισσες αυτές βρίσκονται στην ίδια στήλη. Όμως, πώς διαπιστώνουμε αν δύο βασίλισσες βρίσκονται στην ίδια διαγώνιο;
Ο έλεγχος για το αν δύο βασίλισσες ανήκουν στην ίδια διαγώνιο βασίζεται στην εξής διαπίστωση: Αν θεωρήσουμε οποιαδήποτε θέση μίας διαγωνίου με κατεύθυνση από επάνω αριστερά προς κάτω δεξιά, τότε η διαφορά “γραμμή-στήλη” παραμένει σταθερή. Για παράδειγμα, για τις θέσεις (1,1), (2,2), …, (8,8) της κύριας διαγωνίου που ακολουθεί αυτήν την κατεύθυνση, η διαφορά αυτή ισούται με 0. Επίσης για τις θέσεις (1,2), (2,3), …, (7,8) (αντίστοιχα (2,1), (3,2), … (8,7)) της διαγωνίου που είναι επάνω (αντίστοιχα κάτω) από την προηγούμενη κύρια διαγώνιο, η διαφορά αυτή είναι -1 (αντίστοιχα 1).
Για τις θέσεις των διαγωνίων που έχουν κατεύθυνση από επάνω δεξιά προς κάτω αριστερά παρατηρούμε ότι παραμένει σταθερό το άθροισμα “γραμμή+στήλη”. Για παράδειγμα, για τα στοιχεία (1,8), (2,7), … (8,1) της κύριας διαγωνίου στη συγκεκριμένη κατεύθυνση ισχύει “γραμμή+στήλη”=9. Για τα στοιχεία των διαγωνίων επάνω και κάτω από τη κεντρική αυτή διαγώνιο ισχύει “γραμμή+στήλη”=8 και 10, αντίστοιχα. Έτσι, με βάση τις παρατηρήσεις αυτές, καταλήγουμε ότι αν ισχύει ή , τότε η -οστή και η -οστή βασίλισσα ανήκουν στην ίδια διαγώνιο.
Η λογική συνάρτηση Place1(k) που ακολουθεί, λαμβάνει ως παράμετρο την τιμή k της βασίλισσας που πρόκειται να τοποθετηθεί στη σκακιέρα, ελέγχει τις θέσεις των βασιλισσών στις προηγούμενες γραμμές και επιστρέφει true, αν μπορεί να γίνει η τοποθέτησή της στη στήλη X(k).
function Place1(k);
1. j <-- 1; flag <-- true;
2. while (j<k-1) and (flag=true) do
3. if (X[i]<>X[k]) or (abs(X[i]-X[k])<>abs(i-k))
4. then j <-- j+1
5. else flag <-- false;
6. return flag
Για να καθορισθεί αν ένα διάνυσμα (), με τιμές των (για ) στο διάστημα [1,8], αποτελεί λύση του προβλήματος πρέπει να ελεγχθούν όλα τα ζεύγη των βασιλισσών, οπότε αν βρεθεί έστω και ένα ζεύγος όπου οι βασίλισσες αλληλο-απειλούνται, τότε το διάνυσμα δεν αποτελεί λύση. Ο έλεγχος αυτός γίνεται με την κλήση της λογικής συνάρτησης Solution(X), που έχει παράμετρο το διάνυσμα X και επιστρέφει true, αν το X είναι λύση του προβλήματος.
function Solution(X);
1. i <-- 1; flag <-- true;
2. while (i<=8) and (place1(i)) do i <-- i+1;
3. if i=9 then return true else return false
Η μέθοδος αυτή επίλυσης του προβλήματος μπορεί να υλοποιηθεί με τη χρήση 8 φωλιασμένων εντολών for, όπως φαίνεται στη συνέχεια. Όπως αναφέρθηκε, ο αλγόριθμος αυτός εξετάζει συνολικά 16.777.216 διαφορετικές τοποθετήσεις. Την πρώτη από αυτές, την βρίσκει και την τυπώνει μετά από 1.299.852 δοκιμές.
procedure Queens1;
1. for X[1] <-- 1 to 8 do
2. for X[2] <-- 1 to 8 do
3. for X[3] <-- 1 to 8 do
4. for X[4] <-- 1 to 8 do
5. for X[5] <-- 1 to 8 do
6. for X[6] <-- 1 to 8 do
7. for X[7] <-- 1 to 8 do
8. for X[8] <-- 1 to 8 do
9. if Solution(X) then
10. for j <-- 1 to 8 do
11. write(X[j],' ')
Δεύτερος Αλγόριθμος (Εξαντλητική Αναζήτηση)
Όπως έχει ήδη αναφερθεί, λύσεις του προβλήματος αποτελούν τα διανύσματα () με στοιχεία που είναι διαφορετικά μεταξύ τους και μπορούν να πάρουν τιμές από 1 έως 8, δηλαδή αποτελούν διαφορετικές διατάξεις των ακεραίων 1..8. Αυτό οδηγεί σε μία νέα μέθοδο που στηρίζεται στην εξέταση πολύ λιγότερων καταστάσεων σε σχέση με τις μεθόδους που εξετάσθηκαν προηγουμένως. Το πλήθος των δυνατών καταστάσεων είναι 8!= 40.320.
Μία άλλη προσέγγιση του προβλήματος, λοιπόν, είναι με την κλήση κάποιας διαδικασίας Perm να παραχθούν όλες οι διαφορετικές διατάξεις των αριθμών στο διάνυσμα (1,2,3,4,5,6,7,8). Υπάρχουν πολλές μέθοδοι εύρεσης των διαφορετικών αυτών διατάξεων, οι οποίες λέγονται γεννήτριες διατάξεων (permutation generation). H επόμενη διαδικασία Perm στηρίζεται στην εξής λογική: Θέτει όλες τις τιμές από 1 ως 8 στην πρώτη θέση του διανύσματος και για κάθε τέτοια τοποθέτηση αναδρομικά βρίσκει τις διαφορετικές διατάξεις των 7 στοιχείων του διανύσματος, τα οποία απομένουν. Όταν αναδιαταχθούν τα 8 στοιχεία, τότε τυπώνεται το διάνυσμα που προκύπτει, αν είναι λύση του προβλήματος.
procedure Perm(i);
1. if i=n then
2. if Solution(X) then
3. for j <-- 1 to n do write(X[j],' ')
4. else
5. for j <-- i to n do
6. Swap(X[i],X[j]); Perm(i+1);
7. Swap(X[j],X[i])
Η επόμενη διαδικασία Queens2 αρχικά δίνει την τιμή (1,2,3,4,5,6,7,8) στο διάνυσμα X και καλώντας τη διαδικασία Perm(1) βρίσκει τις διαφορετικές διατάξεις του διανύσματος, τυπώνοντας αυτές που αποτελούν λύση στο πρόβλημα.
procedure Queens2;
1. for i <-- 1 to 8 do X[i] <-- i;
2. Perm(1)
Όπως αναφέρθηκε, ο αριθμός των δυνατών καταστάσεων είναι 40.320, αλλά η πρώτη λύση θα δοθεί μετά από 2.830 δοκιμές. Όμως πέρα από το γεγονός ότι οι λύσεις θα βρεθούν με πολύ λιγότερες δοκιμές σε σύγκριση με τη διαδικασία Queens1, η μέθοδος είναι ταχύτερη, γιατί δεν χρειάζεται η συνάρτηση Place1 να εκτελεί ελέγχους σε σχέση με τις στήλες αλλά μόνο ως προς τις διαγώνιους. Η νέα εκδοχή της συνάρτησης αυτής, Place2, παρουσιάζεται στη συνέχεια.
function Place2(k);
1. j <-- 1; flag <-- true;
2. while (j<k-1) and (flag=true) do
3. if (abs(X[i]-X[k])<>abs(i-k)) then j <-- j+1
4. else flag <-- false;
5. return flag
Τρίτος Αλγόριθμος (οπισθοδρόμηση)
Τέλος, το πρόβλημα των 8 βασιλισσών μπορεί να αντιμετωπιστεί με τη μέθοδο της Οπισθοδρόμησης, σύμφωνα με την οποία αφού τοποθετηθεί μία βασίλισσα, στη συνέχεια ελέγχεται αν υπάρχει επιτρεπτή θέση, για να τοποθετηθεί η επόμενη. Αν βρεθεί τέτοια θέση, τότε ο αλγόριθμος διαχειρίζεται την τοποθέτηση της επόμενης βασίλισσας, διαφορετικά επιστρέφει (δηλαδή, οπισθοδρομεί) στην πιο πρόσφατα τοποθετημένη και την τοποθετεί στη επόμενη δυνατή θέση σε σχέση με αυτή όπου είχε τοποθετηθεί προηγουμένως. Αν τέτοια θέση δεν υπάρχει, τότε γίνεται οπισθοδρόμηση στην αμέσως προηγούμενη κοκ.
Η διαδικασία που υλοποιεί αυτόν τον τρόπο επίλυσης είναι η Queens3. Αυτή χρησιμοποιεί τη συνάρτηση Place1(k), που περιγράφηκε προηγουμένως, για να καθορίσει αν η -οστή βασίλισσα μπορεί να τοποθετηθεί στη στήλη . Η κλήση της Queens3(8) δίνει τη λύση του προβλήματος. Ένα παράδειγμα επίλυσης του προβλήματος των 4 βασιλισσών απεικονίζεται στο Σχήμα 6.9.
procedure Queens3 (n);
1. X[1] <-- 0; k <-- 1;
2. while k>0 do
3. X[k] <-- X[k]+1;
4. while (X[k]<=n) and (not place(k)) do
5. X[k] <-- X[k]+1;
6. if X[k]<=n then
7. if k=n then
8. for i <-- 1 to n do write(X[i],' ')
9. else
10. k <-- k+1; X[k] <-- 0
11. else k <-- k-1 {* backtracking *}
Τέταρτος Αλγόριθμος (δικλάδωση με περιορισμό)
Ο τελευταίος τρόπος επίλυσης μπορεί να βελτιωθεί ακόμη περισσότερο, αν το πλήθος των καταστάσεων του προβλήματος οργανωθεί σε μορφή δένδρου. Σε κάθε επίπεδο του δένδρου από τη ρίζα μέχρι τα φύλλα, οι κόμβοι περιγράφουν μία νόμιμη κατάσταση με 0, 1, 2, κτλ. βασίλισσες τοποθετημένες, ώστε να μην αλληλο-απειλούνται. Όλα τα κλαδιά () του δένδρου είναι τέτοια, ώστε στον κόμβο να περιγράφεται μία κατάσταση για βασίλισσες, ενώ στο κόμβο να περιγράφεται μία κατάσταση με βασίλισσες, η οποία προκύπτει από την προηγούμενη με την προσθήκη μίας επιπλέον βασίλισσας σε επιτρεπτή θέση. Τμήμα του δένδρου αυτού φαίνεται στο επόμενο σχήμα. Παρατηρούμε ότι η ρίζα απεικονίζει την κατάσταση ενός διανύσματος με 0 βασίλισσες και έχει οκτώ παιδιά. Ωστόσο, το πρώτο παιδί έχει μόνον έξι παιδιά καθώς δεν θα ήταν νόμιμη μία κατάσταση με μία βασίλισσα στις θέσεις 2,1 ή 2,2, δεδομένου ότι ήδη υπάρχει μία βασίλισσα στη θέση 1,1. Επεκτείνοντας αυτό το δένδρο προς τα φύλλα, είτε φθάνουμε σε καταστάσεις που οδηγούν σε αδιέξοδο και σταματούμε τις περαιτέρω τοποθετήσεις βασιλισσών, είτε οδηγούμαστε στη λύση.
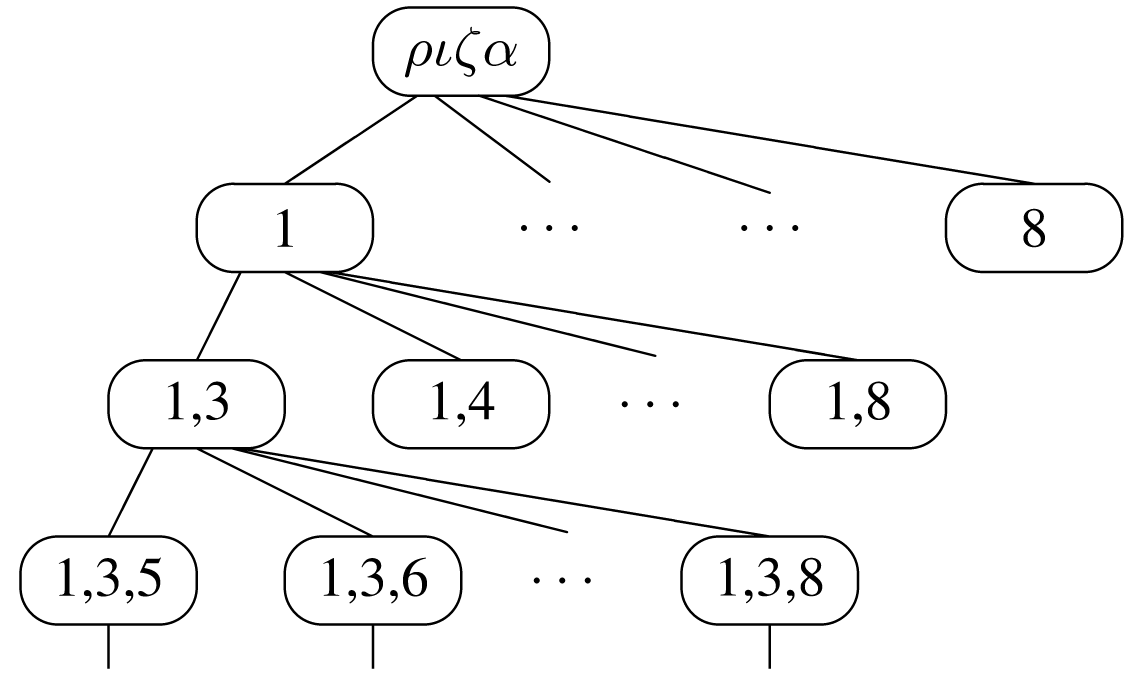
Αυτή η μέθοδος έχει δύο πλεονεκτήματα σε σχέση με τις προηγούμενες. Το πρώτο είναι ότι μειώνει το πλήθος των καταστάσεων, όπου αναζητούνται οι λύσεις του προβλήματος, αφού οι κόμβοι του δένδρου είναι λιγότεροι από 8!=40.320. Για την ακρίβεια, αν με τη βοήθεια του προγράμματος μετρήσουμε τους κόμβους του δένδρου, τότε θα βρούμε ότι είναι μόνο 2057, ενώ η πρώτη λύση θα βρεθεί μετά την εξέταση 114 κόμβων. Το δεύτερο είναι, ότι για να εξετασθεί αν ένας κόμβος του δένδρου, που εκφράζει ένα διάνυσμα μήκους , αντιπροσωπεύει μία νόμιμη κατάσταση, δεν είναι απαραίτητο να ελεγχθούν όλα τα δυνατά ζεύγη μεταξύ των βασιλισσών, αλλά αρκεί να ελεγχθεί αν η -οστή βασίλισσα απειλεί τις προηγούμενες. Αυτός ο έλεγχος μπορεί να γίνει πολύ αποτελεσματικά αν σε κάθε κόμβο αποθηκεύουμε τις διαγωνίους (και των δύο κατευθύνσεων) που ελέγχονται από τις ήδη τοποθετημένες βασίλισσες. Τις διαγωνίους που έχουν κατεύθυνση από κάτω αριστερά προς επάνω δεξιά τις συμβολίζουμε με d45, ενώ με d135 συμβολίζουμε τις διαγωνίους της άλλης κατεύθυνσης. Για να καταλάβουμε την αποτελεσματικότητα αυτής της τεχνικής, αρκεί να σκεφθούμε ότι στις προηγούμενες μεθόδους για να ελέγξουμε αν μία κατάσταση από 8 τοποθετημένες βασίλισσες είναι νόμιμη πρέπει να εκτελέσουμε 28 ελέγχους, στη χειρότερη περίπτωση.
Στη συνέχεια, δίνεται η διαδικασία Queens4 που κωδικοποιεί την τελευταία μέθοδο. Η λύση του προβλήματος λαμβάνεται δίνοντας την κλήση Queens4 ((0,0,0,0,0,0,0,0),0,col,d45,d135) . Προϋποτίθεται ότι οι μεταβλητές col,d45,d135 είναι τύπου συνόλου (πχ. SET of 1..15 στην Pascal).
procedure Queens4(X; k; col,d45,d135);
1. if k=8 then
2. for j <-- 1 to 8 do write(X[j],' ')
2. else
3. for j <-- 1 to 8 do
5. t1 <-- j-k; t2 <-- j+k;
6. if not (j in col) and not (t1 in d45) and
7. not (t2 in d135) then
8. col <-- col+[j]; d135 <-- d135+[t2];
8. d45 <-- d45+[t1]; X[k+1] <-- j;
9. Queens4(X,k+1,col,d45,d135)
Στην προηγούμενη ανάπτυξη των λύσεων του προβλήματος των 8 βασιλισσών δεν έγινε αναφορά στην πολυπλοκότητα των αντίστοιχων μεθόδων. Αν γενικεύσουμε το πρόβλημα και θεωρήσουμε ότι πρέπει να τοποθετηθούν βασίλισσες σε σκακιέρα χωρίς να αλληλο-απειλούνται, τότε σε σχέση με την πολυπλοκότητα αναφέρονται συνοπτικά τα εξής: Η μη αναπτυχθείσα μέθοδος που αναφέρθηκε στην εισαγωγή έχει πολυπλοκότητα της τάξης , άρα πολυπλοκότητα Θ(). Η πρώτη εξαντλητική μέθοδος έχει πολυπλοκότητα Θ(), ενώ η δεύτερη εξαντλητική μέθοδος έχει πολυπλοκότητα . Με απλά λόγια, όλες έχουν την ίδια δραματική πολυπλοκότητα, με διαφορετικό βέβαια σταθερό συντελεστή. Οι δύο τελευταίες μέθοδοι διακρίνονται από εκθετική πολυπλοκότητα.
6.4 Περιοδεύων Πωλητής
Το πρόβλημα του περιοδεύοντος πωλητή (travelling salesperson problem, TSP) ζητά το συντομότερο κύκλο που πρέπει να ακολουθήσει ο πωλητής, ώστε αρχίζοντας από μία πόλη, να περάσει μία φορά από όλες τις πόλεις και να καταλήξει στην αφετηρία. Η έννοια του συντομότερου κύκλου μπορεί να θεωρηθεί ότι δηλώνει τον κύκλο του μικρότερου κόστους, όπου το κόστος μετράται είτε σε ώρες, είτε σε χιλιόμετρα, είτε σε χρήματα κτλ. Θα ακολουθήσει μία λεπτομερής περιγραφή του τρόπου υλοποίησης των διαφόρων λύσεων που μπορούν να δοθούν στο πρόβλημα αυτό.
Θεωρώντας ότι κάθε πόλη είναι ένας κόμβος και ότι οι δρόμοι που ενώνουν δύο πόλεις είναι οι ακμές ενός ζυγισμένου συνδεδεμένου γράφου, το πρόβλημα μετασχηματίζεται στην εύρεση ενός κύκλου στο γράφο αυτό, όπου το άθροισμα των βαρών των ακμών να είναι ελάχιστο. Γενικά, θεωρούμε ότι ο γράφος είναι πλήρης, δηλαδή όλες οι κορυφές ενώνονται μεταξύ τους. Ο γράφος μπορεί να αναπαρασταθεί από έναν πίνακα κόστους , όπου ο αριθμός των κόμβων. Η τιμή κάθε στοιχείου του πίνακα είναι το κόστος της ακμής () του γράφου, όπου μάλιστα είναι δυνατόν να ισχύει . Για τα διαγώνια στοιχεία του πίνακα ισχύει , αλλά ακόμη και αν οι τιμές τους δεν είναι μηδενικές, δεν λαμβάνονται υπ’όψιν, αφού το πρόβλημα απαιτεί επίσκεψη του κάθε κόμβου μόνο μία φορά. Αν δύο πόλεις δεν έχουν απευθείας σύνδεση τότε ισχύει , οπότε δεν επηρεάζεται η λύση του προβλήματος. Στην περίπτωση αυτή, η ζητούμενη διαδρομή είναι ένας κύκλος Hamilton ελαχίστου κόστους.
Πρώτος Αλγόριθμος (άπληστη μέθοδος)
Ο άπληστος αλγόριθμος κάθε φορά επιλέγει από τον πίνακα κόστους την ακμή εκείνη που έχει την ελάχιστη τιμή, από όλες όσες δεν έχουν μέχρι στιγμής εξετασθεί και την προσθέτει στο ήδη σχηματισμένο μονοπάτι, αν:
-
•
δεν υπάρχει στο ήδη σχηματισμένο μονοπάτι άλλη ακμή που να ξεκινά από τον κόμβο ή να καταλήγει στον κόμβο , και
-
•
με την προσθήκη της ακμής () δεν σχηματίζεται κύκλος (εκτός αν είναι η ακμή εκείνη, που με την προσθήκη της σχηματίζεται ο κύκλος που περνά από όλους τους κόμβους του γράφου, δηλαδή ο κύκλος που είναι λύση του προβλήματος).
Με βάση τα προηγούμενα προκύπτει ότι αρχικά πρέπει να έχουμε τις ακμές οργανωμένες, έτσι ώστε να βρίσκουμε εύκολα την ακμή με ελάχιστη τιμή κόστους. Αυτό σημαίνει ότι οι ακμές πρέπει να αποθηκευθούν σε ένα σωρό. Σε μία τέτοια περίπτωση, η εύρεση της κατάλληλης ακμής επιτυγχάνεται με τη βοήθεια της DeleteHeap, που επιστρέφει τα άκρα της ακμής () με το ελάχιστο κόστος, το οποίο ονομάζουμε min.
Οι ακμές που έχουν ήδη προστεθεί στο κύκλο, αποθηκεύονται σε μία λίστα που ορίζεται ως ολική μεταβλητή, την ονομάζουμε Current_Path και είναι τύπου δείκτη Path_Edge που δείχνει προς τη μεταβλητή edge τύπου εγγραφής. Σε κάθε κόμβο, δηλαδή, αποθηκεύεται μία ακμή (), ενώ ο δείκτης next δείχνει στον επόμενο κόμβο της λίστας. Για να προστεθεί μία ακμή () στο μονοπάτι που έχει αναπτυχθεί μέχρι στιγμής, πρέπει να μην υπάρχει στο μονοπάτι αυτό (και επομένως στη λίστα Current_Path) άλλη ακμή της μορφής () ή (). Αυτό συμβαίνει γιατί σε κάθε κύκλο υπάρχει για κάθε κόμβο μία ακμή που καταλήγει σ’ αυτόν και μία που ξεκινά από αυτόν. Έτσι, σαρώνονται όλα τα στοιχεία της λίστας και αν βρεθούν ακμές αυτής της μορφής, τότε η προσθήκη της νέας ακμής απορρίπτεται. Αυτή τη διαδικασία ακολουθεί η λογική συνάρτηση Third_Edge(i,j) που επιστρέφει true αν η ακμή () αποτελεί την τρίτη ακμή που προσπίπτει στον κόμβο ή , οπότε και απορρίπτεται η εισαγωγή της στο μονοπάτι.
function Third_Εdge(u,v);
1. new(p); p <-- Current_Path;
2. counter1 <-- 0; counter2 <-- 0;
3. while (p<>nil) and (count1<=1) and (count2<=1) do
4. if p.i=u then count1 <-- count1+1;
5. if p.j=v then count2 <-- count2+1;
6. p <-- p.next
7. if (count1>=1) or (count2>=1) then return true
8. else return false
Αν η συνάρτηση Third_Edge(i,j) επιστρέψει false, τότε πρέπει να γίνει έλεγχος για το σχηματισμό κύκλου, πριν προστεθεί η ακμή () στο μονοπάτι. Κύκλος σχηματίζεται, όταν υπάρχουν ακμές που να ανήκουν όλες στο μονοπάτι. Αν ο κύκλος αυτός περιέχει όλους τους κόμβους του γράφου, τότε αποτελεί λύση του προβλήματος, αλλιώς απορρίπτεται η εισαγωγή της ακμής ().
Η συνάρτηση Find_Next_Node(v) επιστρέφει έναν κόμβο , αν η ακμή () ανήκει στο μονοπάτι. Αν δεν υπάρχει τέτοια ακμή, τότε επιστρέφει μηδέν, που σημαίνει ότι στην περίπτωση αυτή δεν σχηματίζεται κύκλος και επομένως η ακμή () μπορεί να εισαχθεί στο μονοπάτι.
function Find_Next_Node(u);
1. new(p); p <-- Current_Path;
2. while (p.next<>nil) and (p.i<>u) do p <-- p.next;
3. if p.i=u then return p.j else return 0
Η λογική συνάρτηση Cycle(i,j) χρησιμοποιεί τη συνάρτηση Find_Next_ Node και από τον κόμβο αναπτύσσει το μεγαλύτερο μονοπάτι που μπορεί να αναπτυχθεί, έτσι ώστε όλες οι ακμές του να περιέχονται στο Current_Path. Έστω ότι το μονοπάτι αυτό είναι το . Aν , τότε σχηματίζεται κύκλος, οπότε αν οι κόμβοι είναι ακριβώς οι κόμβοι του γράφου, τότε το μονοπάτι αυτό είναι η λύση του προβλήματος. Αν όμως οι κόμβοι είναι λιγότεροι από τους κόμβους του γράφου, τότε αυτό σημαίνει ότι σχηματίζεται κύκλος που δεν αποτελεί λύση. Έτσι, η συνάρτηση Cycle επιστρέφει true απορρίπτοντας την εισαγωγή της ακμής () στο Current_Path. Αν δεν ισχύει και δεν υπάρχει κόμβος τέτοιος ώστε η ακμή () να περιέχεται στο Current_Path, δηλαδή η κλήση της συνάρτησης Find_Next_Node(kp) επιστρέφει μηδέν, τότε δεν σχηματίζεται κύκλος με την εισαγωγή της () και η Cycle(i,j) επιστρέφει false.
function Cycle(u,v);
1. s <-- [u,v]; a <-- Find_Next_Node(v);
2. while (a<>0) and (a<>u) do
4. s <-- s+[a]; a <-- Find_Next_Node(a)
6. if (a=0) then return false
7. else if (a=u) and (Include_all(s)) then
9. cycle <-- false; solution <-- true
11. else return true;
Η συνάρτηση Cycle καλεί τη λογική συνάρτηση Include_all, που σκοπό έχει να ελέγξει αν στο μονοπάτι περιλαμβάνονται όλες οι κορυφές του γράφου και δίνεται στη συνέχεια. Επίσης, η μεταβλητή s είναι τύπου set, ενώ η λογική μεταβλητή solution είναι καθολική και θα φανεί η χρήση της μέσα στο κύριο πρόγραμμα.
function Include_all(s);
1. Include_all <-- true;
2. while (Include_all=true) and i<=n do
3. if (not (i in s)) then Include_all <-- false;
4. i <-- i+1
Επομένως, η συνολική διαδικασία που ακολουθείται είναι: όσο δεν έχει βρεθεί λύση, επιλέγεται η ακμή με το μικρότερο κόστος μεταξύ αυτών που δεν έχουν εξετασθεί ως τώρα, γίνονται οι δύο έλεγχοι και ανάλογα, είτε γίνεται η εισαγωγή της ακμής στο Current_Path είτε απορρίπτεται. Στη συνέχεια, ακολουθεί το κύριο πρόγραμμα που δένει όλες τις προηγούμενες συναρτήσεις. Getfile είναι η συνάρτηση που διαβάζει το γράφο εισόδου, ο οποίος αναπαρίσταται με τη μέθοδο του πίνακα γειτνίασης.
1. Getfile; new(Current_Path); Current_Path <-- nil;
2. lenght <-- 0; solution <-- false;
3. while (not solution) do
4. DeleteHeap(i,j,min);
5. if not(Third_edge(i,j) and Cycle(i,j)) then
6. new(p); p.i <-- i; p.j <-- j;
7. p.next <-- Current_Path;
8. Current_Path <-- p; length <-- length+min;
9. if solution=true then
10. new(p); p <-- Current_Path;
11. while p<>nil do
12. writeln(p.i,' ',p.j); p <-- p.next
13. writeln('Συνολικό κόστος ',length)
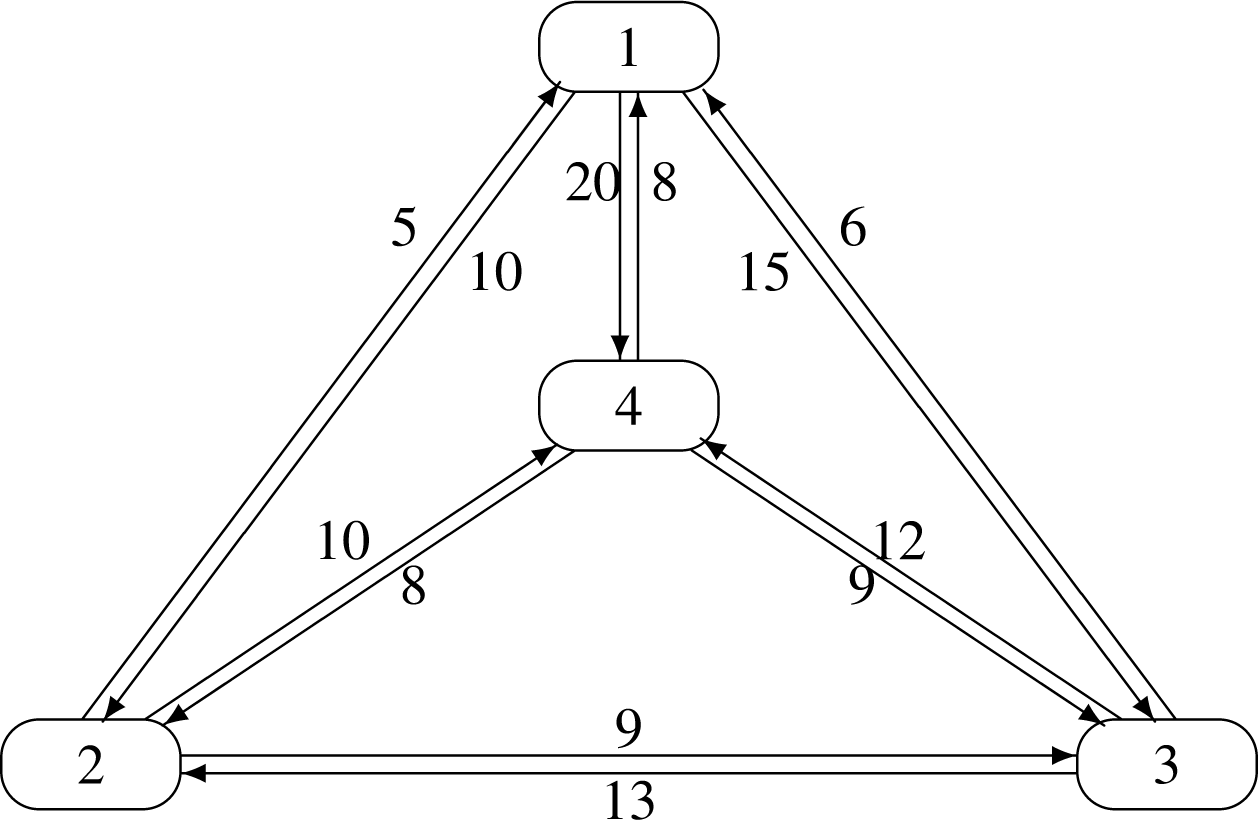
Ας θεωρήσουμε το γράφο του Σχήματος 6.11. Για την επίλυση του TSP για το γράφο αυτό, ο άπληστος αλγόριθμος ακολουθεί την εξής διαδικασία: Η ακμή με το ελάχιστο κόστος είναι η (2,1) με κόστος 5, που είναι η πρώτη ακμή που εισάγεται στο Current_Path. Από αυτές που απομένουν, η ακμή με ελάχιστο κόστος είναι η (3,1), που όμως δεν εισάγεται στο μονοπάτι, γιατί ήδη σε αυτό υπάρχει η (2,1). Για τον ίδιο λόγο απορρίπτεται και η (4,1). Στον Πίνακα 6.3 παρουσιάζονται διάφορα στοιχεία καθώς ο αλγόριθμος εξελίσσεται.
| Ακμή | Κόστος | Ενέργεια |
|---|---|---|
| (2,1) | 5 | Εισάγεται |
| (3,1) | 6 | Απορρίπτεται λόγω του πρώτου ελέγχου |
| (4,1) | 8 | Απορρίπτεται λόγω του πρώτου ελέγχου |
| (4,2) | 8 | Εισάγεται |
| (2,3) | 9 | Απορρίπτεται λόγω του πρώτου ελέγχου |
| (4,3) | 9 | Απορρίπτεται λόγω του πρώτου ελέγχου |
| (1,2) | 10 | Απορρίπτεται λόγω του δεύτερου ελέγχου |
| (2,4) | 10 | Απορρίπτεται λόγω του δεύτερου ελέγχου |
| (3,4) | 12 | Εισάγεται |
| (3,2) | 13 | Απορρίπτεται λόγω του πρώτου ελέγχου |
| (1,3) | 15 | Εισάγεται, τέλος. |
| (1,4) | 20 |
Ο κύκλος που σχηματίζεται αποτελείται από τις ακμές (2,1), (4,2), (3,4) και (1,3), είναι ο (1,3,4,2,1) και έχει μήκος 40. Παρατηρείται ότι ο κύκλος (1,2,4,3,1) έχει μήκος 35. Επομένως ο αλγόριθμος αυτός δεν δίνει πάντα τη βέλτιστη λύση. Γι’αυτόν το λόγο κατατάσσεται στην κατηγορία των προσεγγιστικών ευριστικών άπληστων αλγορίθμων. Ωστόσο, ο αλγόριθμος αυτός είναι χρήσιμος γιατί είναι σχετικά γρήγορος σε σχέση με αυτούς που θα εξετασθούν στη συνέχεια. Πιο συγκεκριμένα, η συνάρτηση DeleteHeap είναι τάξης Ο(), οι συναρτήσεις Third_Edge, Find_Next_Node και Include_All είναι γραμμικές, ενώ η συνάρτηση Cycle είναι τετραγωνικής τάξης. Το τελευταίο προκύπτει από την πράξη βαρόμετρο while p<>nil do. Τελικά, η πολυπλοκότητα της μεθόδου αυτής είναι τάξης Ο(). Η επόμενη λύση δίνει πράγματι τον κύκλο με το μικρότερο κόστος.
Δεύτερος Αλγόριθμος (δυναμικός προγραμματισμός)
Σύμφωνα με τις αρχές του Δυναμικού Προγραμματισμού, τις οποίες γνωρίζουμε από τη Σχεδίαση Αλγορίθμων, το TSP μπορεί να λυθεί κάνοντας χρήση της συνάρτησης:
| (6.2) |
όπου το είναι σύνολο κόμβων. Η συνάρτηση επιστρέφει το κόστος του συντομότερου μονοπατιού που ξεκινά από τον κόμβο , περνά ακριβώς μία φορά από όλους τους κόμβους του συνόλου και καταλήγει στον κόμβο 1, που χωρίς απώλεια της γενικότητας μπορεί να θεωρηθεί ότι ο κύκλος ξεκινά από αυτόν και σε αυτόν καταλήγει. Η συνάρτηση αυτή μπορεί να υλοποιηθεί αναδρομικά ως εξής.
function g(i,s);
1. cost <-- maxint;
2. if s=[] then g <-- C[i,1]
3. else
4. for j <-- 2 to n do
5. if j in s then
6. k <-- C[i,j]+g(j,s-[j]);
7. if k<cost then cost <-- k;
8. g <-- cost
Αν δεν ζητείται μόνο το κόστος της συντομότερης διαδρομής, αλλά και αυτή η ίδια η διαδρομή, τότε πρέπει να ορισθεί μία συνάρτηση , τέτοια ώστε το να ισούται με τον κόμβο που ελαχιστοποιεί το άθροισμα .
Ορίζεται μία λίστα Next_Node του τύπου List_Next_Node, που είναι ένας δείκτης προς μεταβλητές τύπου element, που με τη σειρά του είναι τύπου εγγραφής με τα πεδία node, s, node_min_cost, next. Σε κάθε στοιχείο της λίστας αυτής αποθηκεύονται ο κόμβος (που ελαχιστοποιεί το κόστος ) ως τιμή του πεδίου node_min_cost, ο κόμβος ως τιμή του πεδίου node καθώς επίσης και το σύνολο S.
Για να μην υπολογίζεται μόνο το κόστος του μονοπατιού, αλλά να προσδιορίζεται και το ίδιο το μονοπάτι που έχει ελάχιστο κόστος, χρησιμοποιείται μία παραλλαγή της συνάρτησης g που περιγράφτηκε προηγουμένως. Σύμφωνα με τη νέα παραλλαγή κάθε φορά που βρίσκεται ένας κόμβος που ελαχιστοποιεί το κόστος , προστίθεται στη λίστα Next_Node ένας κόμβος με πεδία που έχουν αντίστοιχα τις τιμές . Αν όμως υπάρχει ήδη στη λίστα κόμβος με τιμές στα δύο πρώτα πεδία τις τιμές και , τότε ενημερώνεται η τιμή του τρίτου πεδίου και γίνεται .
function g(i,s);
1. cost <-- maxint;
2. if s=[] then g <-- C[i,1]
3. else
4. for j <-- 2 to n do if j in s then
5. k <-- C[i,j]+g(j,s-[j]);
6. if k<cost then
7. cost <-- k;
8. if not exist_in_path(i,s,j) then
9. new(p); p.node <-- i; p.s <-- s;
10. next_node <-- p; p.node_min_cost <-- j;
11. p.next <-- next_node
12. g <-- cost
Μετά την κλήση της συνάρτησης αυτής έχει υπολογισθεί το κόστος του συντομότερου κύκλου και έχουν βρεθεί οι τιμές των κόμβων που ελαχιστοποιούν τα αθροίσματα για κάθε κόμβο του γράφου και για κάθε σύνολο κόμβων . Ο συντομότερος κύκλος είναι , . Για να βρεθεί, γίνεται αναζήτηση στους κόμβους της λίστας Next_Node, όπως φαίνεται από τον κώδικα της διαδικασίας Search(i,S) που ακολουθεί.
procedure Search(i,s);
1. new(p); p <-- next_node;
2. while ((p.next<>nil) and ((p.node<>i) or (p.s<>s)))
3. do p <-- p.next;
4. if (p.node=i) and (p.s=s) then
5. write(p.node_min_cost,' ');
6. Search(p.node_min_cost,s-[p.node_min_cost]);
Για το γράφο του προηγούμενου σχήματος, οι τιμές της συνάρτησης J παρουσιάζονται στον Πίνακα 6.4, οπότε ο συντομότερος κύκλος που βρίσκει ο αλγόριθμος είναι (1,2,4,3,1) με κόστος 35.
| J(2,[3])=3 | J(3,[2])=2 | J(4,[2])=2 | J(2,[3,4])=4 | J(4,[2,3])=2 |
| J(2,[4])=4 | J(3,[4])=4 | J(4,[3])=2 | J(3,[2,4])=4 | J(1,[2,3,4])=2 |
Επιλογικά, στη βιβλιογραφία αναφέρονται και άλλες επακριβείς λύσεις που στηρίζονται στη μέθοδο της οπισθοδρόμησης και στη μέθοδο της διακλάδωσης και του περιορισμού. Το γεγονός είναι ότι το TSP είναι ένα κλασικό NP-complete πρόβλημα και επομένως δεν μπορεί κανείς να είναι αισιόδοξος ότι θα βρει αποδοτικούς αλγορίθμους για μία γενική λύση του. Οι τεχνικές που περιγράψαμε εδώ δίνουν μία αρκετά ικανοποιητική προσεγγιστική λύση για μικρές (σχετικά) τιμές. Επειδή το πρόβλημα έχει πολλές πρακτικές εφαρμογές, έχει απασχολήσει πολλούς ερευνητές σε μία προσπάθεια να πετύχουν λύσεις σε όλο και μεγαλύτερα στιγμιότυπα του προβλήματος. Το 1954 οι Dantzig, Fulkerson και Johnson έλυσαν το πρόβλημα για 42 πόλεις των ΗΠΑ, ενώ το 1980 οι Padberg και Hong το έλυσαν για 318 πόλεις. Το 1992 οι Applegate, Bixby, Cook από το Πανεπιστήμιο Rice, και ο Chvatal από το Πανεπιστήμιο Rutgers βρήκαν τη βέλτιστη διαδρομή για 3.038 πόλεις των ΗΠΑ, χρησιμοποιώντας ένα σύστημα από 50 σταθμούς εργασίας. Το 1993 ανέβασαν τον αριθμό των πόλεων σε 4.461 πόλεις, ενώ το 1994 ανέβασαν τον αριθμό αυτό σε 7.397 πόλεις. Αυτό το ρεκόρ είχε μείνει ακατάρριπτο μέχρι το 1998. Με τη βοήθεια 3 ισχυρών μηχανών (Digital AlphaServer 4100 με 12 επεξεργαστές) και ένα σύνολο από 12 προσωπικούς υπολογιστές Pentium II, οι οποίοι έτρεχαν το πρόγραμμα για περίπου 3 μήνες, οι τέσσερις ερευνητές πέτυχαν να δώσουν λύση στο πρόβλημα για τις 13.509 πόλεις των ΗΠΑ με πληθυσμό περισσότερο από 500 κατοίκους.
6.5 Βιβλιογραφική Συζήτηση
Στο παρόν κεφάλαιο παρουσιάσθηκαν οι γνωστές τεχνικές σχεδίασης αλγορίθμων μέσα από μία engineering προσέγγιση για την επίλυση μερικών προβλημάτων, με σκοπό τη σταδιακή παραγωγή βελτιωμένης λύσης. Με παρόμοια προσέγγιση θα μπορούσε να επιλυθεί πλήθος άλλων προβλημάτων. Αντί άλλης βιβλιογραφικής παραπομπής συνιστάται η ανάγνωση του άρθρου [179], που συνεγράφη από τον Tarjan με την ευκαιρία της βράβευσής του με το Turing award, όπου συνοπτικά παρουσιάζεται όλο το πανόραμα του αντικειμένου.
Ειδικότερα για το πρόβλημα του μέγιστου αθροίσματος υποακολουθίας εξετάσθηκε εξαντλητικά στο βιβλίο του Bentley [13], όπου μπορούν να βρεθούν αποτελέσματα από τις δοκιμές των υλοποιήσεων των αλγορίθμων. Τονίζεται ότι στα βιβλία του Bentley [12, 13, 14] παρουσιάζονται ενδιαφέρουσες τεχνικές σχεδιασμού αλλά και κωδικοποίησης αλγορίθμων, σε μια βήμα προς βήμα βελτίωση του τελικού αποτελέσματος. Ακόμη, σχετικό υλικό υπάρχει στην προσωπική σελίδα του Bentley (www.programmingpearls.com/teaching.html). Επίσης το πρόβλημα μελετάται σε βάθος και στα βιβλία των Weiss [195] και Cohen [30], αλλά με περισσότερο θεωρητικό και μεθοδολογικό τρόπο. Επίσης, το άρθρο [120] αναφέρεται στο ίδιο πρόβλημα.
Το πρόβλημα των 8 βασιλισσών είναι ένα κλασικό πρόβλημα για τη γνωστική περιοχή της Τεχνητής Νοημοσύνης (Artificial Intelligence) με μακρά ιστορία, καθώς ασχολήθηκε με αυτό ο Gauss το 1859. Στα πλαίσια του παρόντος βιβλίου εξετάζεται σε σχέση με τις γνωστές αλγοριθμικές τεχνικές. Το αντικείμενο εξετάζεται στο βιβλίο [199] καθώς και στα άρθρα [67, 176].
Το βιβλίο των Lawler-Lenstra-Rinnooy Kan-Shmoys [95] αναφέρεται αποκλειστικά στο πρόβλημα του περιοδεύοντος πωλητή. Επίσης, στο βιβλίο των Moret-Shapiro [130] υπάρχει εκτενής αναφορά στο ίδιο πρόβλημα (σελίδες 256-261). Ειδικότερα, αναφέρεται η υλοποίηση μίας εξάδας άπληστων τεχνικών, ενώ τα αποτελέσματα τους συγκρίνονται με την επίδοση της βέλτιστης λύσης για ένα σύνολο 9 και 57 πόλεων των ΗΠΑ.
Οι Ασκήσεις 2-3 (το πρόβλημα της Ολλανδικής σημαίας) αναφέρονται στο βιβλίο [69], η Άσκηση 9 στο [23], η Άσκηση 10 για το πρόβλημα των 9 κερμάτων στα άρθρα [36, 73], η Άσκηση 13 στο άρθρο [58], ενώ η Άσκηση 14 στο βιβλίο [195]. Οι Ασκήσεις 6-7, που επεκτείνουν το πρόβλημα της εύρεσης του μέγιστου αθροίσματος υποακολουθίας, έχουν τεθεί αντιστοίχως στον Πανελλήνιο Διαγωνισμό Πληροφορικής του 1999 και στη Διεθνή Ολυμπιάδα Πληροφορικής του 1994, ενώ η Άσκηση 12 έχει τεθεί στη Βαλκανική Ολυμπιάδα Πληροφορικής του 1994.
6.6 Ασκήσεις
-
1.
Να σχεδιασθούν και να αναλυθούν εναλλακτικοί αλγόριθμοι για την εύρεση των πενταψηφίων αριθμών, των οποίων το τετράγωνο αποτελείται από δέκα ανόμοια ψηφία. Οι αριθμοί αυτοί ονομάζονται καρκινικοί.
-
2.
Δίνονται δύο ταξινομημένοι πίνακες A[0..n-1] και B[0..m-1]. Κάθε πίνακας αποτελείται από διακριτά στοιχεία. Να σχεδιασθούν και να αναλυθούν εναλλακτικοί αλγόριθμοι για την εύρεση του πλήθους των κοινών στοιχείων μεταξύ των δύο πινάκων.
-
3.
Δίνεται ένας πίνακες A[0..n-1], όπου κάθε στοιχείο είναι έχει τιμή ένα από τα χρώματα: άσπρο, μπλε και κόκκινο. Να σχεδιασθούν και να αναλυθούν εναλλακτικοί αλγόριθμοι, ώστε με τις κατάλληλες αντιμεταθέσεις, να έρθουν στην αρχή τα κόκκινα στοιχεία και στο τέλος τα μπλε.
-
4.
Δίνεται πίνακας Α με στοιχεία και ζητείται το δεύτερο μικρότερο (). Να σχεδιασθούν και να αναλυθούν δύο αλγόριθμοι για το πρόβλημα. Ο ένας να εκτελεί μια κατάλληλη σάρωση του πίνακα (Ωμή Βία), ενώ ο άλλος να στηρίζεται στη αρχή του Διαίρει και Βασίλευε.
-
5.
Να σχεδιασθούν και να αναλυθούν εναλλακτικοί αλγόριθμοι για τον υπολογισμό:
-
–
του ελάχιστου αθροίσματος υποακολουθίας,
-
–
του ελάχιστου θετικού αθροίσματος υποακολουθίας, και
-
–
του μέγιστου γινομένου υποακολουθίας.
-
–
-
6.
Δίνεται ένας τετραγωνικός πίνακας A[0..n-1,0..n-1] με θετικούς και αρνητικούς ακέραιους. Να βρεθεί ο υποπίνακας (δηλαδή, με διάσταση από 1x1 μέχρι nxn) με το μεγαλύτερο άθροισμα στοιχείων. Να σχεδιασθούν και να αναλυθούν εναλλακτικές λύσεις.
7 3 8 8 1 4 2 7 4 4 4 5 2 6 5 Σχήμα 6.12: Το πρόβλημα του τριγώνου. -
7.
Το Σχήμα 6.12 παρουσιάζει ένα αριθμητικό τρίγωνο, όπου η -οστή γραμμή περιέχει ακεραίους. Ζητείται να υπολογισθεί το μεγαλύτερο άθροισμα αριθμών επάνω σε μία διαδρομή, που ξεκινά από την κορυφή και τερματίζει κάπου στη βάση. Μία διαδρομή προσδιορίζεται σε κάθε βήμα από τη μετακίνηση διαγωνίως είτε κάτω αριστερά είτε κάτω δεξιά. Να σχεδιασθούν δύο αλγόριθμοι επίλυσης του προβλήματος που να βασίζονται στην Ωμή Βία και στο Δυναμικό Προγραμματισμό.
-
8.
Δίνεται ένας πίνακας A[0..n-1] που περιέχει τους αριθμούς από 1 μέχρι n. Να βρεθεί ο αριθμός των αντιστροφών (inversions), δηλαδή των περιπτώσεων όπου A[i]<A[j] αλλά i>j. Να σχεδιασθούν και να αναλυθούν εναλλακτικές λύσεις που να στηρίζονται στη μέθοδο της Ωμής Βίας και τη μέθοδο Διαίρει και Βασίλευε.
-
9.
Μία αυτόματη μηχανή πωλήσεων δέχεται νομίσματα των 10, 20 και 50 λεπτών. Ποιός είναι το πλήθος των διαφορετικών τρόπων που μπορούμε να τροφοδοτήσουμε τη μηχανή με λεπτά, όπου το είναι πολλαπλάσιο του 10; Να σχεδιασθούν και να αναλυθούν δύο λύσεις, με Αναδρομή και με Δυναμικό Προγραμματισμό.
-
10.
Ένας πίνακας 3x3 περιλαμβάνει 9 κέρματα. Αρχικά στην επάνω όψη άλλα κέρματα δείχνουν γράμματα και άλλα κορώνα. Ζητείται μία δεδομένη αρχική κατάσταση των κερμάτων να μετατραπεί σε μία τελική, όπου όλα τα κέρματα έχουν τα γράμματα στην επάνω όψη, κάνοντας τον ελάχιστο αριθμό αλλαγών όψεων. Με τον όρο “αλλαγή όψεων” (flip) εννοούμε ότι όταν γυρίζουμε ένα κέρμα, ταυτόχρονα γυρίζουμε και τα γειτονικά του που βρίσκονται προς τα επάνω, κάτω, αριστερά και δεξιά (όσα από αυτά υπάρχουν). Στον Πίνακα 6.5 παρουσιάζονται αριθμημένες οι θέσεις του πίνακα. Για παράδειγμα, γειτονικές της θέσης 5 είναι οι θέσεις 2, 4, 6 και 8, ενώ της θέσης 3 είναι οι 2 και 6, και της θέσης 2 είναι οι 1, 3 και 5. Να δοθούν λύσεις που να βασίζονται σε Δυναμικό Προγραμματισμό και Οπισθοδρόμηση.
1 2 3 4 5 6 7 8 9 Πίνακας 6.5: Το πρόβλημα με τα 9 κέρματα. -
11.
Για το πρόβλημα του υπολογισμού για ρέστα με τον ελάχιστο αριθμό κερμάτων αναφέρονται στη βιβλιογραφία δύο λύσεις: με Άπληστη Μέθοδο και με Δυναμικό Προγραμματισμό. Ποιά είναι καλύτερη σύμφωνα με αναλυτικά κριτήρια; Δίνουν και οι δύο μέθοδοι πάντοτε τη βέλτιστη λύση; Για το σχεδιασμό και την ανάλυση των δύο αλγορίθμων να θεωρηθούν οι εξής δύο σειρές νομισμάτων: (α) 1, 2, 5, 10, 20, 50 λεπτά, και (β) 1, 5, 25, 50 λεπτά.
-
12.
Έστω ένα γραμμικό δίκτυο υπολογιστών, όπου ο κάθε υπολογιστής συνδέεται ακριβώς με δύο άλλους, εκτός από τους δύο ακραίους υπολογιστές που συνδέονται μόνο με έναν. Η απόσταση μεταξύ δύο υπολογιστών και δίνεται από το στοιχείο A[i,j] του πίνακα A[0..n-1,0..n-1], όπου . Το πρόβλημα έγκειται στην εύρεση του τρόπου σύνδεσης των υπολογιστών, ώστε σε μία τέτοια ανοικτή αλυσίδα να ελαχιστοποιηθεί το μήκος του απαιτούμενου καλωδίου. Υπόψη ότι το καλώδιο θα πρέπει να τοποθετηθεί κάτω από το πάτωμα, οπότε το συνολικό μήκος του καλωδίου που χρειάζεται για τη σύνδεση δύο διαδοχικών υπολογιστών ισούται με την απόσταση μεταξύ των υπολογιστών συν 10 μέτρα επιπλέον. Να σχεδιασθεί και να αναλυθεί αλγόριθμος για την επίλυση του προβλήματος.
-
13.
Δίνεται το έτος γέννησης και το έτος θανάτου κροκοδείλων. Σκοπός είναι ο υπολογισμός του μέγιστου πλήθους ζώντων κροκοδείλων σε οποιαδήποτε χρονική στιγμή. Να σχεδιασθούν και να αναλυθούν αλγόριθμοι για την επίλυση του προβλήματος. Να θεωρηθεί ότι: (α) όλες οι χρονολογίες είναι διακριτές και ανήκουν στο διάστημα [-100000..2000], και (β) τα δεδομένα εισόδου αποθηκεύονται σε ένα πίνακα A[1..2,0..n-1].
-
14.
Έστω ότι πρέπει να παράξουμε όλες τις δυνατές διατάξεις αριθμών με τη βοήθεια ενός πίνακα Α[0..n-1]. Για το σκοπό αυτό θα χρησιμοποιηθεί η γεννήτρια τυχαίων αριθμών rant_int(i,j), η οποία ισοπίθανα γεννά τους ακέραιους από μέχρι . Σχεδιάζουμε τους εξής 3 αλγορίθμους:
-
–
Γεμίζουμε από την αρχή μία-μία τις θέσεις του πίνακα A. Προκειμένου να γεμίσουμε τη θέση , (όπου, ) καλούμε τη γεννήτρια rant_int που δίνει έναν τυχαίο ακέραιο. Ελέγχουμε σειριακά τον πίνακα μέχρι τη συγκεκριμένη θέση μήπως ο ακέραιος αυτός έχει ήδη εισαχθεί. Αν δεν έχει εισαχθεί, τότε τον αποθηκεύουμε στη θέση , αλλιώς καλούμε εκ νέου τη συνάρτηση.
-
–
Όπως προηγουμένως, αλλά διατηρούμε έναν επιπλέον πίνακα που ονομάζουμε used. Για κάθε εισαγόμενο τυχαίο αριθμό ran, θέτουμε used[ran]=1. Επομένως, ο έλεγχος μήπως έχει ήδη εισαχθεί κάποιος ακέραιος γίνεται άμεσα και όχι σειριακά.
-
–
Αρχικοποιούμε τον πίνακα ως εξής: A[i]=i+1. Κατόπιν εκτελούμε τις εντολές:
for (i=1; i<n; i++) swap(&A[i], &A[rand_int(0,i)]);
Να αναλυθούν οι αλγόριθμοι και να δοθούν οι σχετικοί συμβολισμοί Ο.
-
–