Κεφάλαιο 5Αλγόριθμοι Χαμηλού Επιπέδου
Στο Κεφάλαιο 1.4 αναφέραμε το περιβάλλον εργασίας μας. Δηλαδή, ότι υποθέτουμε ένα μοντέλο μηχανής RAM, μίας μηχανής με έναν επεξεργαστή όπου οι εντολές εκτελούνται σειριακά. Αναφερθήκαμε, επίσης, στην ποικιλία των στοιχειωδών εντολών που για λόγους απλοποίησης θεωρούμε ότι έχουν μοναδιαίο κόστος. Έτσι, η πολυπλοκότητα ενός αλγορίθμου εξαρτάται από το πλήθος των στοιχειωδών πράξεων που καταμετρούμε, ώστε να φθάσουμε σε μία έκφραση συναρτήσει του μεγέθους της εισόδου . Στο σημείο αυτό θα ανοίξουμε μία παρένθεση για να διερευνήσουμε περαιτέρω τις υποθέσεις αυτές.
5.1 Αριθμητικοί Αλγόριθμοι
Σε περιπτώσεις αναζήτησης ή ταξινόμησης είναι λογικό να θεωρούμε ως μέγεθος του
προβλήματος το αντίστοιχο πλήθος των στοιχείων εισόδου. Επίσης σε περιπτώσεις διάσχισης
ενός δένδρου ή ενός γράφου είναι λογικό να θεωρούμε ως μέγεθος του προβλήματος το πλήθος
των κορυφών ή/και το πλήθος των ακμών. Ωστόσο, για ένα μεγάλο σύνολο αλγορίθμων που
αφορούν σε αριθμητικές πράξεις, όπως για παράδειγμα η παραγοντοποίηση ενός αριθμού, η
εύρεση του μέγιστου κοινού διαιρέτη, οι πράξεις modulo, ο έλεγχος για πρώτους αριθμούς,
ο πολλαπλασιασμός πινάκων ή ακόμη απλούστερα ο πολλαπλασιασμός δύο ακεραίων, προκύπτει
ότι η καλύτερη μέθοδος για την εύρεση της πολυπλοκότητας είναι η θεώρηση του πλήθους
των bits που είναι απαραίτητα για την αναπαράσταση των αντίστοιχων αριθμών σε δυαδική
μορφή. Χωρίς την ανάλυση αυτών των αλγορίθμων σε χαμηλό επίπεδο, δηλαδή σε επίπεδο
πράξεων bit, δεν θα μπορούσε να γίνει μία αντικειμενική ανάδειξη της πολυπλοκότητας
του αντίστοιχου αλγορίθμου. Το σκεπτικό αυτό θα γίνει καλύτερα κατανοητό με το παράδειγμα.
Στο Κεφάλαιο 4.5 παρουσιάσαμε τον επόμενο αλγόριθμο factorial2 για τον υπολογισμό του παραγοντικού για και καταλήξαμε ότι η πολυπλοκότητά του είναι γραμμική Θ(). Ωστόσο, στο σημείο εκείνο έγινε σιωπηρά η υπόθεση ότι κάθε πράξη πολλαπλασιασμού (εντολή 2) απαιτεί σταθερό χρόνο εκτέλεσης ανεξαρτήτως του μεγέθους των τελεστών. Όμως, είναι αυτό ρεαλιστικό, δηλαδή να θεωρούμε σταθερό το κόστος πολλαπλασιασμού δύο αριθμών καθώς μας ενδιαφέρει το πλήθος των δεδομένων εισόδου και όχι το μέγεθος εκάστου ενός των δεδομένων εισόδου;
function factorial2(n);
1. product <-- 1;
2. for i <-- 1 to n do product <-- i*product;
3. return product
5.2 Κόστος Στοιχειωδών Πράξεων
Αρχικά, θα εξετάσουμε και θα θυμηθούμε τη λειτουργία των τεσσάρων βασικών πράξεων (πρόσθεση, αφαίρεση, πολλαπλασιασμός και διαίρεση), ώστε να συναγάγουμε το κόστος τους θεωρώντας το μέγεθος των αριθμών που υπεισέρχονται σε κάθε πράξη. Στην επόμενη παράγραφο, θα χρησιμοποιήσουμε το υλικό αυτής της παραγράφου για να μελετήσουμε σύνθετους αριθμητικούς αλγορίθμους.
Δεδομένου ενός ακεραίου αριθμού ισχύει ότι . Επομένως, για να αναπαραστήσουμε έναν ακέραιο σε δυαδική μορφή χρειαζόμαστε bits, όπου .
Πρόσθεση Ακεραίων
Από όλα τα κλασικά διδακτικά βιβλία Αρχιτεκτονικής Υπολογιστών γνωρίζουμε τι είναι οι αθροιστές (adders). Για παράδειγμα, έστω ότι δίνονται δύο ακέραιοι αριθμοί υπό δυαδική μορφή και που αντιστοιχούν στους ακεραίους και υπό δεκαδική μορφή. Ο -οστός αθροιστής που δέχεται εισόδους τα και , όπου είναι το κρατούμενο από τον προηγούμενο αθροιστή. Στο Σχήμα 5.1 παρουσιάζεται η πρόσθεση δύο ακεραίων σε δεκαδικό και δυαδικό σύστημα. Είναι προφανής η σάρωση των δυαδικών αριθμών από τα δεξιά προς τα αριστερά. Συνεπώς, η πολυπλοκότητα της πρόσθεσης είναι γραμμική ως προς το μήκος σε bits των τελεσταίων, δηλαδή Θ(), με μία κρυμμένη σταθερά ίση με 2 λόγω του κρατούμενου .
8 1000
+3 +0011
-- ----
11 1011
αφαίρεση πρόσθεση πρόσθεση
αριθμών συμπληρώματος μονάδας
8 1000 1000 0100
-3 -0011 +1100 +1
-- ---- ---- ----
5 1011 0100 0101
Αφαίρεση Ακεραίων
Η πράξη της αφαίρεσης είναι παρόμοια προς την πράξη της πρόσθεσης και στηρίζεται στο συμπλήρωμα. Στο Σχήμα 5.2 παρουσιάζεται η αντίστοιχη διαδικασία. Το συμπλήρωμα, όπως και η διαδικασία της πρόσθεσης, ουσιαστικά είναι μία σάρωση, άρα είναι μία γραμμική διαδικασία, ενώ η τελική πρόσθεση του άσσου έχει σταθερό κόστος. Συνεπώς, η πολυπλοκότητα είναι τελικά και πάλι γραμμική, δηλαδή Θ().
Πολλαπλασιασμός Ακεραίων
Έστω δύο ακέραιοι αριθμοί υπό δυαδική μορφή και που δίνονται προς πολλαπλασιασμό. Οι αριθμοί τοποθετούνται στους καταχωρητές Α και Β, αντίστοιχα, ενώ στον καταχωρητή Ρ θα τοποθετηθεί το γινόμενό τους. Ο πολλαπλασιασμός θα γίνει με τα εξής δύο βήματα:
-
1.
αν το λιγότερο σημαντικό ψηφίο του Α είναι 1, τότε ο καταχωρητής Β προστίθεται στο Ρ, αλλιώς προστίθεται το 00…00. Το άθροισμα τίθεται πάλι στον καταχωρητή Ρ.
-
2.
οι καταχωρητές Α και Ρ ολισθαίνουν προς τα δεξιά, ενώ το κρατούμενο του αθροίσματος μετακινείται στο υψηλότερο (αριστερότερο) bit του καταχωρητή Ρ και το χαμηλότερο bit του Ρ μετακινείται στον καταχωρητή Α, όπου το δεξιότερο bit διολισθαίνει προς τα έξω καθώς δεν θα χρησιμοποιηθεί στη συνέχεια.
Μετά από βήματα, το γινόμενο εμφανίζεται στους καταχωρητές Ρ και Α, όπου ο Α αποθηκεύει τα λιγότερο σημαντικά ψηφία του αποτελέσματος. Το Σχήμα 5.3 δείχνει τον πολλαπλασιασμό δύο ακεραίων, των A=6 και B=3, τους οποίους παριστούμε με τους αντίστοιχους δυαδικούς 110 και 011. Εφόσον το μήκος των αριθμών σε bits είναι 3, έπεται ότι θα υπάρξει ένας βρόχος τριών επαναλήψεων των δύο βημάτων. Το τελικό αποτέλεσμα είναι 010010, δηλαδή 18. Παρατηρούμε ότι για κάθε bit του A εκτελείται μία πρόσθεση όλων των bits του B. Συνεπώς, η πολυπλοκότητα του πολλαπλασιασμού δύο ακεραίων που αναπαριστώνται με και bits αντίστοιχα είναι Θ().
A B P
Βήμα 1 (πρόσθεση Β στο Ρ) 110 011 000
Βήμα 2 (ολίσθηση δεξιά) 011 011 000
Βήμα 1 (πρόσθεση Β στο Ρ) 011 011 011
Βήμα 2 (ολίσθηση δεξιά) 101 011 001
Βήμα 1 (πρόσθεση Β στο Ρ) 101 011 100
Βήμα 2 (ολίσθηση δεξιά) 010 011 010
Διαίρεση Ακεραίων
Στην πράξη της διαίρεσης δύο δυαδικών αριθμών, με μία διαδικασία παρόμοια προς την προηγούμενη, οι αριθμοί τοποθετούνται στους καταχωρητές Α και Β, ενώ το αποτέλεσμα τοποθετείται στον καταχωρητή Ρ. Η διαίρεση θα γίνει με τα εξής τέσσερα βήματα:
-
1.
ολισθαίνουμε το ζεύγος των καταχωρητών Α και Ρ μία θέση προς τα αριστερά.
-
2.
αφαιρούμε το περιεχόμενο του καταχωρητή Β από τον καταχωρητή Ρ και τοποθετούμε το αποτέλεσμα στον καταχωρητή Ρ.
-
3.
αν το αποτέλεσμα του προηγούμενου βήματος είναι αρνητικό, τότε βάζουμε 0 στο χαμηλότερο ψηφίο του Α, αλλιώς βάζουμε το 1.
-
4.
αν το αποτέλεσμα του ιδίου βήματος είναι αρνητικό, τότε αποκαθιστούμε την παλιά τιμή του Ρ προσθέτοντας το περιεχόμενο του Β στο Ρ.
Για παράδειγμα, έστω ότι θέλουμε να διαιρέσουμε τους αριθμούς A=14=1110 και B=3=11. Το Σχήμα 5.4 παρουσιάζει την αλληλουχία των βημάτων. Στο τέλος των τεσσάρων (όσο το μήκος του A) επαναλήψεων των τεσσάρων βημάτων στον καταχωρητή Α είναι αποθηκευμένο το πηλίκο (δηλαδή 4), ενώ στον καταχωρητή Ρ είναι αποθηκευμένο το υπόλοιπο (δηλαδή 2).
Ρ Α Β
Αρχική κατάσταση 00 1110 11
Βήμα 1 (ολίσθηση αριστερά) 01 110 11
Βήμα 2 (αφαίρεση Β από Ρ) -10 110 11
Βήμα 3 (χαμηλό bit του A) -10 1100 11
Βήμα 4 (αποκατάσταση Ρ) 01 1100 11
Βήμα 1 (ολίσθηση αριστερά) 11 100 11
Βήμα 2 (αφαίρεση Β από Ρ) 00 100 11
Βήμα 3 (χαμηλό bit του A) 00 1001 11
Βήμα 1 (ολίσθηση αριστερά) 01 001 11
Βήμα 2 (αφαίρεση Β από Ρ) -10 001 11
Βήμα 3 (χαμηλό bit του A) -10 0010 11
Βήμα 4 (αποκατάσταση Ρ) 01 0010 11
Βήμα 1 (ολίσθηση αριστερά) 10 010 11
Βήμα 2 (αφαίρεση Β από Ρ) -01 010 11
Βήμα 3 (χαμηλό bit του A) -01 0100 11
Βήμα 4 (αποκατάσταση Ρ) 10 0100 11
Στο παράδειγμα αυτό, σαρώνουμε φορές (δηλαδή, όσο το μέγεθος σε bits του
καταχωρητή Α) τον καταχωρητή Ρ μεγέθους bits (δηλαδή, όσο το μέγεθος σε bits του
καταχωρητή Β). Συνεπώς, όπως και στην περίπτωση του πολλαπλασιασμού, η πολυπλοκότητα
της διαίρεσης δύο ακεραίων που αναπαριστώνται με και bits αντίστοιχα είναι
Θ().
5.3 Κόστος Βασικών Αλγορίθμων
Στην παράγραφο αυτή θα επανεξετάσουμε αλγορίθμους που ήδη έχουμε μελετήσει στα προηγούμενα μαθήματα, αλλά τώρα η επανεξέταση θα γίνει κάτω από το νέο πρίσμα για την κοστολόγηση των πράξεων.
Υπολογισμός Δύναμης
Θέλουμε να υπολογίσουμε τη δύναμη , όπου τα είναι ακέραιοι αριθμοί. Ας υποθέσουμε ότι θα εφαρμόσουμε τη γνωστή συνάρτηση power1, που την υπενθυμίζουμε στη συνέχεια, ώστε να αντιληφθούμε το μηχανισμό του υπολογισμού αυτού.
function power1(a,b)
1. power <-- 1;
2. for i <-- 1 to b do power <-- power*a
3. return power1
Με βάση όσα αναφέραμε προηγουμένως για το κόστος του πολλαπλασιασμού προκύπτει ότι για να υπολογίσουμε το τετράγωνο χρειαζόμαστε Θ() πράξεις σε bit, ενώ το μέγεθος του αποτελέσματος έχει μέγεθος bits. Ομοίως, για τον υπολογισμό του θα εκτελέσουμε έναν πολλαπλασιασμό μεταξύ δύο αριθμών: ενός αριθμού μεγέθους bits και ενός αριθμού μεγέθους bits. Συνεπώς, το αντίστοιχο υπολογιστικό κόστος θα είναι πράξεις με bit (με κρυμμένη σταθερά 2), ενώ το αποτέλεσμα της πράξης θα αποθηκευθεί σε χώρο bits. Συνεχίζοντας το σκεπτικό αυτό καταλήγουμε στο συμπέρασμα ότι για τον υπολογισμό του θα εκτελέσουμε έναν πολλαπλασιασμό μεταξύ δύο αριθμών: ενός αριθμού μεγέθους bits και ενός αριθμού bits. Συνεπώς, η χρονική πολυπλοκότητα της ύψωσης σε δύναμη είναι Θ(), ενώ η χωρική πολυπλοκότητα είναι Θ().
Υπολογισμός Αθροίσματος
Θέλουμε να υπολογίσουμε το άθροισμα . Αρχικά μελετάμε το αριστερό σκέλος. Με βάση τα προηγούμενα, προκύπτει ότι το κόστος υπολογισμού του ενός τετραγώνου είναι Θ() και, επομένως, το συνολικό κόστος για τον υπολογισμό όλων των τετραγώνων του αριστερού σκέλους θα είναι Θ(). Καθώς το κόστος των προσθέσεων προσθέσεων είναι μικρότερο από το κόστος των πολλαπλασιασμών, προκύπτει ότι το προηγούμενο κόστος είναι και το τελικό σε σχέση με το αριστερό σκέλος. Απεναντίας, το κόστος υπολογισμού του δεξιού σκέλους είναι Θ(), γεγονός που εξηγείται με βάση το γεγονός ότι απλώς εκτελούνται τρεις πολλαπλασιασμοί και μία διαίρεση.
Πολλαπλασιασμός Πινάκων
Ας υποθέσουμε ότι πρέπει να πολλαπλασιάσουμε δύο τετραγωνικούς πίνακες , ενώ το μέγεθος των στοιχείων των πινάκων είναι μικρότερο από . Ο πίνακας που θα προκύψει από τον πολλαπλασιασμό θα έχει επίσης στοιχεία, κάθε ένα από τα οποία για να υπολογισθεί απαιτεί πολλαπλασιασμούς και προσθέσεις. Επειδή κάθε πολλαπλασιασμός απαιτεί πράξεις με bit, ενώ κάθε πρόσθεση απαιτεί πράξεις με bit, έπεται ότι το συνολικό κόστος είναι πράξεις με bits, και επομένως η πολυπλοκότητα είναι .
Υπολογισμός Συνδυασμού
Θεωρούμε γνωστή την Εξίσωση 2.35 για τον υπολογισμό του συνδυασμού των ανά αντικειμένων:
| (5.1) |
και απο το Κεφάλαιο 4.5 χρησιμοποιούμε τη γνωστή συνάρτηση comb4, που υπενθυμίζουμε στη συνέχεια.
function comb4(n,m);
1. if m>n-m then m <-- n-m
2. t1 <-- 1;
3. for i <-- n downto n-m+1 do t1 <-- t1*i;
4. t2 <-- factorial2(m);
5. return t1/t2
Σύμφωνα με τον αλγόριθμο αυτό αρχικά εκτελούνται πολλαπλασιασμοί για τον αριθμητή, στη συνέχεια άλλοι πολλαπλασιασμοί για τον παρονομαστή και τελικά μία διαίρεση. Αν υποθέσουμε ότι το μέγεθος του είναι bits, τότε με τη λογική που αντιμετωπίσαμε το πρόβλημα του υπολογισμού της ύψωσης σε δύναμη θα έχουμε τον εξής μηχανισμό.
Για να εκτελέσουμε τον πρώτο πολλαπλασιασμό χρειαζόμαστε Θ() πράξεις σε bit, ενώ το μέγεθος του αποτελέσματος θα έχει μέγεθος bits. Για το δεύτερο πολλαπλασιασμό θα θεωρήσουμε έναν αριθμό μεγέθους bits και έναν αριθμό μεγέθους bits. Συνεπώς, το αντίστοιχο κόστος θα είναι πράξεις με bit (με κρυμμένη σταθερά 2), ενώ το αποτέλεσμα της πράξης θα αποθηκευθεί σε χώρο bits. Συνεχίζοντας το σκεπτικό αυτό καταλήγουμε στο συμπέρασμα ότι για την εκτέλεση του ()-οστού πολλαπλασιασμού θα θεωρήσουμε έναν αριθμό μεγέθους bits και έναν αριθμό μεγέθους bits. Συνεπώς, η χρονική πολυπλοκότητα για τον υπολογισμό του αριθμητή θα είναι , δηλαδή ισχύει η πολυπλοκότητα Θ(). Το κόστος του υπολογισμού του παρονομαστή (εντολή 4) είναι ασφαλώς φραγμένο από επάνω από την ίδια πολυπλοκότητα του υπολογισμού του αριθμητή, δηλαδή Θ(). Επομένως αυτή είναι και η τελική απάντηση σε σχέση με τη ζητούμενη πολυπλοκότητα.
Μετατροπή Δυαδικού σε Δεκαδικό Αριθμό
Ας υποθέσουμε ότι δίνεται ένας ακέραιος υπό τη δυαδική μορφή και επιθυμούμε να βρούμε την ισοδύναμή του έκφραση στο δεκαδικό σύστημα. Θα μπορούσε να εφαρμοσθεί ένας αλγόριθμος της επόμενης μορφής.
function bin2dec
1. num <-- b_{k-1};
2. for i <-- k-2 downto 0 do num <-- 2*num + b_i;
Καθώς κάθε μερικό αποτέλεσμα είναι μεγέθους το πολύ bits και ο βρόχος εκτελείται φορές, έπεται ότι ο συνολικός αριθμός πράξεων με bit είναι .
Εύρεση Μέγιστου Κοινού Διαιρέτη
Στο Κεφάλαιο 4.1 μελετήσαμε διεξοδικά τον αλγόριθμο του Ευκλείδη για την εύρεση του μέγιστου κοινού διαιρέτη μεταξύ δύο ακεραίων . Στο σημείο αυτό υπενθυμίζουμε τον αλγόριθμο.
function euclid(m,n)
1. while m>0 do
2. t <-- n mod m
3. n <-- m
4. m <-- t
5. return n
Για να προχωρήσουμε σε μία εκτίμηση κόστους, κατ’αρχήν πρέπει να παρατηρήσουμε ότι στις διαδοχικές διαιρέσεις παράγονται συνεχώς μικρότερα υπόλοιπα. Επίσης, στο Κεφάλαιο 4.1 παρατηρήσαμε ότι . Με λίγα λόγια, μετά από κάθε δεύτερο βήμα το υπόλοιπο υποδιαιρείται και επομένως στη χειρότερη περίπτωση θα εκτελεσθούν διαιρέσεις. Καθώς σε κάθε τέτοιο βήμα οι αριθμοί που υπεισέρχονται στις διαιρέσεις αυτές είναι μικρότεροι του , έπεται ότι κάθε τέτοια πράξη απαιτεί στη χειρότερη περίπτωση Ο(). Επομένως, τελικά η πολυπλοκότητα είναι Ο(). Σημειώνουμε ότι με μία πιο σφικτή ανάλυση μπορεί να προκύψει ότι η πολυπλοκότητα είναι Ο().
Εύρεση Πρώτων Αριθμών
Από την Άσκηση 1.12 γνωρίζουμε ότι για την εύρεση
των πρώτων αριθμών από 1 ως , μπορεί να χρησιμοποιηθεί το κόσκινο του Ερατοσθένη.
Ο μικρότερος πρώτος αριθμός είναι 2. Έτσι, αγνοούμε όλα τα πολλαπλάσια του 2 μέχρι
την τιμή . Από τους αριθμούς που απομένουν ο μικρότερος είναι και πάλι πρώτος,
δηλαδή το 3. Έτσι αγνοούμε όλα τα πολλαπλάσια του 3 μέχρι την τιμή . Σύμφωνα με
το επόμενο θεώρημα, η διαδικασία αυτή πρέπει να συνεχισθεί για όλους τους ακεραίους
μέχρι το , καθώς αυτό το όριο αρκεί για τον Ερατοσθένη.
Θεώρημα.
Αν το είναι θετικός σύνθετος ακέραιος, τότε ο έχει έναν πρώτο αριθμό που δεν
ξεπερνά το .
Απόδειξη.
Αν το είναι θετικός σύνθετος ακέραιος, τότε ισχύει , όπου
. Συνεπώς, γιατί αλλιώς θα έπρεπε .
Ο έλεγχος ενός αριθμού για την εύρεση των πρώτων αριθμών του με τη μέθοδο του Ερατοσθένη είναι πολύ αναποτελεσματικός. Αν με Π() συμβολίζουμε το πλήθος των πρώτων αριθμών που δεν υπερβαίνουν τον αριθμό , τότε για να ελέγξουμε αν ο είναι πρώτος αρκεί να εκτελέσουμε Π() διαιρέσεις. Έχει αποδειχθεί ότι ασυμπτωτικά ισχύει και επομένως το πλήθος των πρώτων αριθμών που δεν υπερβαίνουν τον αριθμό είναι . Καθώς κάθε τέτοια διαίρεση απαιτεί Θ() πράξεις με bit, είναι ευνόητο ότι συνολικά απαιτούνται Θ() πράξεις με bit, με την προϋπόθεση ότι διαθέτουμε μία λίστα με όλους τους πρώτους αριθμούς που δεν υπερβαίνουν την τιμή . Η πολυπλοκότητα αυτή είναι εκθετική ως προς , ενώ αν διεκπεραιώναμε το πρόβλημα θεωρώντας μία συμβατική προσέγγιση για την ανάλυση του αλγορίθμου, τότε θα καταλήγαμε σε μία γραμμική πολυπλοκότητα.
5.4 Βιβλιογραφική Συζήτηση
Η οπτική γωνία αυτού του κεφαλαίου δεν είναι η συνήθης στη διεθνή βιβλιογραφία. Η αντιμετώπιση της σχεδίασης και ανάλυσης αλγορίθμων γενικώς βασίζεται σε μία περισσότερο «υψηλή» προσέγγιση. Το υλικό του κεφαλαίου αυτού στηρίζεται σε μεγάλο βαθμό στα άρθρα [27, 28] και για την κατανόησή του απαιτούνται στοιχειώδεις γνώσεις αρχιτεκτονικής. Το βιβλίο των Dasgupta-Παπαδημητρίου-Vazirani αφιερώνει σημαντικό χώρο στο αντικείμενο [35]. Σημειώνεται ότι η παρουσίαση του σχετικού υλικού στο τελευταίο βιβλίο γίνεται με στόχο την ανάπτυξη των θεμελιώσεων της κρυπτογραφίας [177].
5.5 Ασκήσεις
-
1.
Να αποδειχθεί ότι σε κάθε αριθμητικό σύστημα με βάση , το άθροισμα τριών οποιωνδήποτε μονοψήφιων αριθμών είναι αριθμός διψήφιος το πολύ.
-
2.
Να αποδειχθεί ότι κάθε αριθμός στο δυαδικό σύστημα έχει τετραπλάσιο το πολύ μήκος από τον αντίστοιχο δεκαδικό. Ποιό είναι το όριο αυτών των δύο μηκών για μεγάλους αριθμούς;
-
3.
Έστω ότι ένας ακέραιος αριθμός των bits λαμβάνει οποιαδήποτε τιμή στο διάστημα [] με την ίδια πιθανότητα. Να υπολογισθούν τα εξής:
-
–
Ποιά είναι η πιθανότητα για την -οστή θέση (όπου ) να είναι 0 και ποιά να είναι 1;
-
–
Ποιά είναι η μέση τιμή του πλήθους των ‘1’ στα bits;
-
–
Ποιά είναι η προσδοκητή τιμή της θέσης του αριστερότερου ‘1’;
-
–
-
4.
Στις ψηφιακές οθόνες κάθε ακέραιος παρίσταται με ένα συνδυασμό επτά φωτεινών γραμμών. Οι γραμμές αυτές αριθμούνται από 0 ως 6 όπως φαίνεται στο Σχήμα 5.5. Να σχεδιασθεί και να αναλυθεί ένας αλγόριθμος που να δέχεται ένα θετικό ακέραιο των 16 bits και να δίνει ένα πίνακα από 5 bytes. Το -οστό bit του -οστού byte θα πρέπει να είναι 1, αν και μόνο αν η -οστή γραμμή της παράστασης είναι φωτεινή.
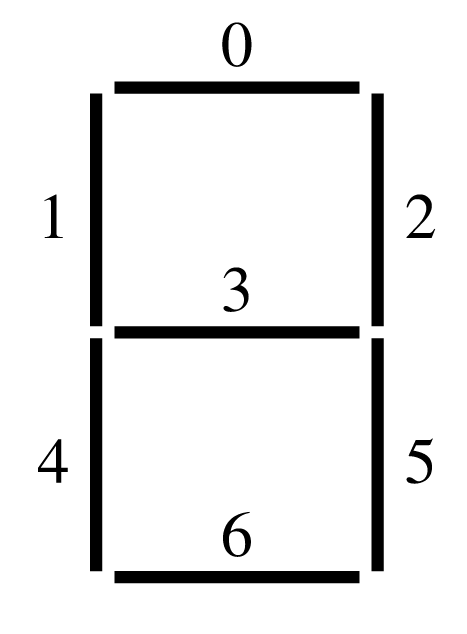
Σχήμα 5.5: Το πρόβλημα του πίνακα matrix. -
5.
Να σχεδιασθεί και να αναλυθεί αλγόριθμος υπολογισμού του συμπληρώματος ως προς 2 ενός ακεραίου που βρίσκεται στο διάστημα [].
-
6.
Δίνονται δύο αριθμοί () και (). Ποιά είναι η πολυπλοκότητα της πρόσθεσης και του πολλαπλασιασμού τους αν ;
-
7.
Σε κρυπτογραφικές εφαρμογές απαιτείται ο υπολογισμός του , όπου συχνά τα μπορεί να έχουν μήκος 100άδες bits. Να σχεδιασθεί και να αναλυθεί σχετικός αλγόριθμος εφαρμόζοντας διαδοχικούς υπολογισμούς του . Να σχολιασθεί και η χρονική αλλά και η χωρική πολυπλοκότητα.
-
8.
Ο ΜΚΔ δύο ακεραίων μπορεί να υπολογισθεί επίσης σύμφωνα με τον τύπο:
(5.2) Να σχεδιασθεί ένας αλγόριθμος που να υλοποιεί αυτόν τον τύπο. Να συγκριθεί η επίδοση αυτού του αλγορίθμου σε σχέση με αυτήν του αλγορίθμου του Ευκλείδη, υπό την προϋπόθεση ότι οι αριθμοί και είναι ακέραιοι των bits.
-
9.
Με βάση τη λογική του ψευδοκώδικα power4(a,b) του Κεφαλαίου 4.4 διατυπώνουμε τη σχέση:
(5.3) Η σχέση αυτή να χρησιμοποιηθεί για τη σχεδίαση και την ανάλυση αλγορίθμου που να βασίζεται στη λογική Διαίρει και Βασίλευε και να υπολογίζει το . Να γίνει σύγκριση με τον αλγόριθμο της Άσκησης 8 ως προς τη χρονική αλλά και τη χωρική πολυπλοκότητα.
-
10.
Με βάση τη λογική του ψευδοκώδικα factorial2(n) του Κεφαλαίου 4.5 να διατυπωθεί η πολυπλοκότητα του υπολογισμού του , ως συνάρτηση του μήκους της δυαδικής αναπαράστασης του . Πόσα bits απαιτούνται για την αναπαράσταση του .
-
11.
Να αποδειχθεί ότι αν (όπου όλα τα είναι θετικοί ακέραιοι), τότε είτε είτε . Να σχεδιασθεί και να αναλυθεί αλγόριθμος που να διαπιστώνει αν ένας θετικός ακέραιος είναι δύναμη.
-
12.
Να σχεδιασθεί και να αναλυθεί αλγόριθμος εύρεσης του ΕΚΠ δύο θετικών ακεραίων μεγέθους bits.