Κεφάλαιο 13Τυχαίοι Αλγόριθμοι

Διακρίνουμε τρεις κατηγορίες τυχαίων αλγορίθμων, τους αλγορίθμους τύπου Las Vegas, τύπου Monte Carlo και τύπου Sherwood. Οι αλγόριθμοι Las Vegas πάντοτε δίνουν την ίδια (σωστή) έξοδο για τα ίδια δεδομένα εισόδου, απλώς ο χρόνος εκτέλεσης εξαρτάται από την έξοδο της γεννήτριας των τυχαίων αριθμών. Απεναντίας οι αλγόριθμοι Monte Carlo απαιτούν το ίδιο χρόνο εκτέλεσης ανεξαρτήτως της εξόδου της γεννήτριας των τυχαίων αριθμών, αλλά δεν δίνουν πάντοτε την ίδια έξοδο για τα ίδια δεδομένα εισόδου. Προφανώς, η ιδιότητα αυτή δεν είναι επιθυμητή, γιατί άλλοτε ο αλγόριθμος θα δίνει τη σωστή λύση και άλλοτε κάποια λανθασμένη.

Λέγεται λοιπόν ότι ένα αλγόριθμος Las Vegas (Monte Carlo) αποτυγχάνει αν δεν τερματίζει εντός ενός συγκεκριμένου χρονικού διαστήματος (αν δεν δίνει τη σωστή απάντηση). Η απαίτησή μας είναι οι αντίστοιχοι αλγόριθμοι να αποτυγχάνουν με κάποια πολύ μικρή πιθανότητα, δηλαδή $n^{-a}$, για δεδομένη τιμή της παραμέτρου $a$.

Τέλος, η κατηγορία αλγορίθμων Sherwood περιλαμβάνει αλγορίθμους που πάντοτε δίνουν απάντηση και η απάντηση αυτή είναι σωστή. Συχνά σε αιτιοκρατικούς αλγορίθμους η χειρότερη περίπτωση είναι σημαντικά χειρότερη από τη μέση περίπτωση. Ενσωματώνοντας, λοιπόν, την τυχαία επιλογή μίας γεννήτριας (με μηδαμινό κόστος) είναι δυνατόν να εξαλειφθεί η διαφορά μεταξύ της χειρότερης και της μέσης περίπτωσης. Καθώς μία τέτοια τεχνική βοηθά σε μία περισσότερο ομαλή εκτέλεση του αιτιοκρατικού αλγορίθμου, δεν τίθεται ζήτημα θεώρησης της κατανομής της πιθανότητας ο αλγόριθμος να μην τερματίσει ή να δώσει λανθασμένα αποτελέσματα.

Αυτή είναι η βάση των τυχαίων αλγορίθμων, των οποίων η ανάλυση είναι μία εναλλακτική οπτική γωνία στην ανάλυσης της μέσης περίπτωσης, όπου για την ευκολία μας μπορεί να υιοθετήσουμε περιοριστικές υποθέσεις. Οι τυχαίοι αλγόριθμοι έχουν καλύτερη και χειρότερη περίπτωση αλλά τα δεδομένα εισόδου που προκαλούν τις περιπτώσεις αυτές είναι άγνωστα και μπορεί να είναι οποιαδήποτε ακολουθία μεγέθους $n$.

Έστω ότι ένας πίνακας με $n$ στοιχεία περιέχει $n/2+1$ διακριτά στοιχεία, όπου τα $n/2$ έχουν την ίδια τιμή. Το ζητούμενο είναι να βρούμε ποιά είναι η τιμή που εμφανίζεται $n/2$ φορές. Είναι εύκολο να σχεδιάσουμε έναν αιτιοκρατικό αλγόριθμο που να σαρώνει τον πίνακα και να διαπιστώνει ποιά είναι αυτή η τιμή μετά από $n/2+2=\mathrm{O}(n)$ βήματα στη χειρότερη περίπτωση. Αυτή η περίπτωση ανταποκρίνεται στην κατάσταση όπου οι πρώτες $n/2+1$ θέσεις του πίνακα καταλαμβάνονται από αντίστοιχες διακριτές τιμές, ενώ η ($n$/2+2)-οστή είναι η πρώτη επανάληψη της πολλαπλής τιμής.

Τώρα θα εξετάσουμε έναν τυχαίο αλγόριθμο, δηλαδή έναν αλγόριθμο που στηρίζεται σε μία γεννήτρια τυχαίων αριθμών. Έστω, λοιπόν, ότι επιλέγουμε με τυχαίο τρόπο δύο διαφορετικές θέσεις του πίνακα και ελέγχουμε αν το περιεχόμενό τους είναι ίδιο. Αν πράγματι το περιεχόμενο είναι ίδιο, τότε αλγόριθμος τερματίζει, αλλιώς πρέπει το δειγματοληπτικό πείραμα να συνεχισθεί για όσο χρειασθεί. Προφανώς, ο αλγόριθμος αυτός ανήκει στην κατηγορία Las Vegas, δηλαδή ο αλγόριθμος είναι βέβαιο ότι τερματίζοντας δίνει τη σωστή απάντηση αλλά δεν είναι σταθερός ο απαιτούμενος χρόνος. Η επόμενη διαδικασία παρουσιάζει αυτήν την περιγραφή.

     procedure repeatedelement
1.   flag <-- true;
2.   while flag do
3.      i <-- random(1,n); j <-- random(1,n)
4.      if (i<>j) and (A[i]=A[j]) then
5.         flag <-- false; return A[i]

Η πιθανότητα ότι μία δοκιμή θα είναι επιτυχής, δηλαδή θα εξακριβώσει τη ζητούμενη τιμή ισούται με $p=\frac{n/2}{n}\frac{n/2-1}{n}=\frac{n/2-1}{2n}$. Διαπιστώνεται, δηλαδή, ότι για $n=10$, ισχύει $p=0.2$, άρα σε μία τέτοια περίπτωση πρέπει να επαναλάβουμε τη δοκιμή με πιθανότητα 0.8. Η πιθανότητα ο αλγόριθμος να μην τερματίσει μετά από 10 δοκιμές είναι ${(1-p)}^{10}\approx 0.11$ και, άρα, η πιθανότητα να τερματίσει είναι 0.89 περίπου. Αντίστοιχα, η πιθανότητα να μην τερματίσει μετά από 100 δοκιμές είναι ${(1-p)}^{100}\approx 2\times {10}^{-10}$.

Στη γενική περίπτωση, η πιθανότητα να μην τερματίσει ο αλγόριθμος μετά από $ca\log n$ βήματα (για κάποια σταθερά $c$) είναι

$${(4/5)}^{ca\log n}=n^{-ca\log (5/4)}$$

(13.1)

που δίνει $n^{-a}$, αν $c=1/\log (5/4)$. Συνεπώς, με πιθανότητα μεγαλύτερη από $1-n^{-a}$, ο αλγόριθμος θα τερματίσει στη χειρότερη περίπτωση μετά από $\frac{a\log n}{\log (5/4)}$ πειράματα. Έτσι, θεωρώντας ως βαρόμετρο την εντολή 5, προκύπτει ότι η πολυπλοκότητα του τυχαίου αυτού αλγορίθμου είναι Ο$(\log n)$.

Στην παράγραφο αυτή θα εξετάσουμε ένα παρεμφερές με το προηγούμενο πρόβλημα. Έστω ότι δίνεται ένας πίνακας με $n$ στοιχεία. Λέγεται ότι ο πίνακας αυτός έχει ένα πλειοψηφικό (majority) στοιχείο, αν ένα στοιχείο του εμφανίζεται περισσότερο από $n/2$ φορές. Είναι, όμως, ενδεχόμενο να μην υπάρχει πλειοψηφικό στοιχείο στον πίνακα. Ας μελετήσουμε τον επόμενο αλγόριθμο.

     function maj
1.   i <-- random(1,n); x <-- A[i]; k <-- 0;
2.   for j <-- 1 to n do
3.      if A[j]=x then k <-- k+1
4.   return (k>n/2)

Αν ο πίνακας δεν έχει πλειοψηφικό στοιχείο, τότε ο αλγόριθμος maj ορθώς θα επιστρέψει false. Ωστόσο, αν ο πίνακας έχει πλειοψηφικό στοιχείο, τότε ο αλγόριθμος θα επιστρέψει true, αλλά το αποτέλεσμα θα είναι ορθό με πιθανότητα $p>1/2$. Όμως λάθος ίσο με 50% δεν μπορεί να είναι αποδεκτό. Προχωρούμε σε μία δεύτερη εκδοχή.

     function maj2
1.   if maj then return true
2.   else return maj

Αν ο πίνακας δεν έχει πλειοψηφικό στοιχείο, τότε ο αλγόριθμος maj2 ορθώς θα επιστρέψει false, τιμή που ορθώς θα του περάσει ο αλγόριθμος maj. Από την άλλη πλευρά, αν ο πίνακας πράγματι έχει πλειοψηφικό στοιχείο και ορθώς ο αλγόριθμος maj επιστρέψει τιμή true, τότε και αλγόριθμος maj2 θα επιστρέψει true. Αν όμως με πιθανότητα $p>1/2$ ο αλγόριθμος maj επιστρέψει τιμή false, τότε o αλγόριθμος maj2 θα ξανακαλέσει τον αλγόριθμο maj που θα επιστρέψει και πάλι true ή false πιθανότητα $p>1/2$ και $1-p$ αντίστοιχα. Στην περίπτωση αυτή θα λάβουμε ορθό αποτέλεσμα με πιθανότητα $p+(1-p)p>3/4$. Επομένως, επιτύχαμε σημαντική βελτίωση στην αξιοπιστία του αρχικού αλγορίθμου.  

Η τελική μας εκδοχή είναι ο επόμενος αλγόριθμος Monte Carlo. Υποθέτουμε ότι $ϵ>0$ είναι η μέγιστη ανοχή της πιθανότητας λάθους. Είναι προφανές ότι η πολυπλοκότητα του αλγορίθμου είναι Ο($n\log (1/ϵ)$). Ο αλγόριθμος αυτός έχει μόνο διδακτική σπουδαιότητα, καθώς είναι εύκολο να σχεδιάσουμε έναν αιτιοκρατικό αλγόριθμο με γραμμική πολυπλοκότητα.

     function majMC
1.   k <-- log(1/e)
2.   for j <-- 1 to k do
3.      if maj then return true
4.   return false

Γνωρίζουμε από το μάθημα των Δομών Δεδομένων ότι μπορούμε να αναπαραστήσουμε μία δυναμική λίστα με τη βοήθεια ενός πίνακα. Ας μελετήσουμε την τεχνική αυτή με ένα παράδειγμα. Στο Σχήμα 13.1 παρουσιάζεται ένας δισδιάστατος πίνακας A με τα γνωστά 9 κλειδιά 52, 12, 71, 56, 5, 10, 19, 90 και 45, τα οποία εμφανίζονται στην πρώτη γραμμή του πίνακα. Στη δεύτερη γραμμή παρουσιάζονται κάποιες τιμές που προσομοιώνουν τον κλασικό δείκτη των δυναμικών συνδεδεμένων λιστών. Ακολουθώντας αυτούς τους τεχνητούς δείκτες μπορούμε να πάρουμε τα στοιχεία σε αύξουσα διάταξη. Για να γίνει δυνατή η προσπέλαση και η επεξεργασία της δομής, είναι απαραίτητο να έχουμε και μία βοηθητική μεταβλητή header που να δίνει τη θέση του μικρότερου στοιχείου της δομής. Στην περίπτωση μας ισχύει header=5. Επίσης, παρατηρούμε ότι ο δείκτης του μεγαλύτερου στοιχείου είναι 0 ώστε να διευκολύνει το πέρας της προσπέλασης.

Η επόμενη διαδικασία αναζητά το κλειδί key που υπάρχει πράγματι στη δομή και επιστρέφει τη θέση του κλειδιού στη δομή. Είναι εύκολο να εξαχθεί η επίδοση της αναζήτησης στη δομή αυτή. Προφανώς στη μέση (χειρότερη) περίπτωση θα πρέπει να σαρωθεί ο μισός (ολόκληρος) ο πίνακας και, επομένως, η αναζήτηση είναι γραμμική Θ($n$).

     function search(key, header)
1.   i <-- header
2.   while key > A[1,i] do i <-- A[2,i]
3.   return i

Μία τυχαιοποιημένη εκδοχή έχει ως εξής.

     function searchrandom(key)
1.   i <-- random(1,n); y <-- A[1,i]
2.   if key<y then return search(key,header)
3.   else if key>y then return search(key,A[2,i])
4.   else return i

Εύκολα και πάλι προκύπτει ότι η νέα τυχαιοποιημένη συνάρτηση είναι γραμμικής πολυπλοκότητας. Ωστόσο, πληρώνοντας το αμελητέο κόστος της εντολής 1, η διαδικασία επιταχύνεται κατά 50% κατά μέσο όρο. Η συνάρτηση αυτή στηρίζεται στη φιλοσοφία Sherwood.

Όπως είναι γνωστό από το μάθημα των Δομών Δεδομένων, η διαδικασία της διαγραφής σε δυαδικό δένδρο αναζήτησης είναι πιο σύνθετη από τη διαδικασία της εισαγωγής. Αν ο κόμβος που πρόκειται να διαγραφεί είναι τερματικός, τότε η περίπτωση είναι εύκολη. Επίσης σχετικά εύκολη είναι η περίπτωση που ο διαγραφόμενος κόμβος έχει μόνο έναν απόγονο. Η δυσκολία του προβλήματος παρουσιάζεται, όταν το στοιχείο που θα διαγραφεί έχει δύο απογόνους. Στην περίπτωση αυτή το διαγραφόμενο κλειδί αντικαθίσταται από το κλειδί του πιο δεξιού κόμβου του αριστερού υποδένδρου, ο οποίος (όπως μπορεί να αποδειχθεί) έχει το πολύ έναν απόγονο.

Στη συνέχεια, δίνεται η αναδρομική διαδικασία delete που καλεί την επίσης αναδρομική διαδικασία del, όταν o κόμβος με το κλειδί key έχει δύο απογόνους. Έτσι, ανιχνεύεται ο προηγούμενος λεξικογραφικά κόμβος, δηλαδή ο δεξιότερος κόμβος του αριστερού υποδένδρου του κόμβου q που πρόκειται να διαγραφεί. Αν ο κόμβος αυτός είναι ο r, τότε το περιεχόμενό του αντικαθιστά το περιεχόμενο του q και ο χώρος του r επιστρέφεται στο σύστημα. Για την κατανόηση αναφέρεται ότι θεωρείται κόμβος με τρία πεδία (data,left,right), ακέραιου τύπου και τύπου δείκτη.

     procedure del(r)
1.   if r.right<>nil then del(r.right)
2.   else
3.      q.data <-- r.data; q <-- r; r <-- r.left

     procedure delete(key,p);
1.   if p=nil then write('Το κλειδί ',key,'δεν υπάρχει')
2.   else if key<p.data then delete(key,p.left)
3.   else if key>p.data then delete(key,p.right)
4.   else
5.      q:=p;
6.      if q.right=nil then p:=q.left
7.      else if q.left=nil then p:=q.right
8.      else del(q.left);
9.      dispose(q)

Για παράδειγμα στο επόμενο σχήμα δίνεται η διαδικασία της διαδοχικής διαγραφής των κλειδιών 19, 52, 5 και 12 από το αρχικό δένδρο.

Ο τρόπος υλοποίησης της διαδικασίας της διαγραφής δεν είναι ο μοναδικός. Για παράδειγμα, αν το υπό διαγραφή κλειδί έχει και αριστερό αλλά και δεξιό υποδένδρο, τότε αυτό ισοδύναμα θα μπορούσε να αντικατασταθεί από τον επόμενο λεξικογραφικά κόμβο, δηλαδή τον αριστερότερο κόμβο του δεξιού υποδένδρου. Αυτές οι δύο εναλλακτικές υλοποιήσεις ονομάζονται ασύμμετρες (asymmetric), σε αντίθεση με τη μέθοδο της συμμετρικής (symmetric) διαγραφής, σύμφωνα με την οποία το υπό διαγραφή κλειδί αντικαθίσταται με τον προηγούμενο ή τον επόμενο λεξικογραφικά κόμβο είτε εναλλάξ είτε με τυχαίο τρόπο (δηλαδή με 50%-50% πιθανότητα να χρησιμοποιηθεί ο αριστερός ή ο δεξιός υποψήφιος). Η υλοποίηση της συμμετρικής τυχαίας διαγραφής από δυαδικό δένδρο αναζήτησης είναι εύκολη υπόθεση για τον αναγνώστη.

Έχει αποδειχθεί ότι αν από τυχαίο δένδρο με $n$ κόμβους διαγραφεί ένα κλειδί με την ασύμμετρη μέθοδο, τότε δεν προκύπτει ένα τυχαίο δένδρο. Πιο συγκεκριμένα, το μήκος εσωτερικού μονοπατιού δεν παραμένει τάξης Ο($n\log n$) αλλά αυξάνει. Εμπειρικές μελέτες από τον Eppinger (1983) έδειξαν ότι αν χρησιμοποιηθεί η ασύμμετρη μέθοδος διαγραφής, τότε το μήκος εσωτερικού μονοπατιού γίνεται τάξης O($n{\log }^{3}n$). Αντίθετα, αν χρησιμοποιηθεί η συμμετρική μέθοδος διαγραφών, τότε το μήκος εσωτερικού μονοπατιού πράγματι παραμένει O($n\log n$). Συνεπώς, η τεχνική της τυχαιοποιημένης διαγραφής δεν είναι χωρίς επίπτωση στη συνολική επίδοση της δομής κατά τις αναζητήσεις.

Πίσω από την συμμετρική διαγραφή βρίσκεται η φιλοσοφία των αλγορίθμων Sherwood. Στα επόμενα δύο παραδείγματα θα ασχοληθούμε με κλασικότερα παράδειγμα τυχαίων αλγορίθμων που ανήκουν σε μία από τις δύο άλλες κατηγορίες που αναφέρθηκαν, δηλαδή τις κατηγορίες Las Vegas ή Monte Carlo.

Στο σημείο αυτό θα ασχοληθούμε με δυαδικά δένδρα αναζήτησης, τα οποία βασίζονται στις τυχαίες επιλογές που κάνει ο αλγόριθμος κατά την κατασκευή τους. Τα συγκεκριμένα τυχαία δένδρα ονομάζονται Δένδρα Αναζήτησης Σωρού (ΔΑΣ για συντομία - treaps) και παρουσιάζονται αναλυτικά στο [167].

Έστω $X$ ένα σύνολο με $n$ στοιχεία, όπου το καθένα απαρτίζεται από ένα κλειδί και μία προτεραιότητα. Ένα ΔΑΣ για το $X$ είναι ένα δυαδικό δένδρο με $n$ κόμβους, το οποίο είναι δομημένο με ενδοδιάταξη ως προς τα κλειδιά και με διάταξη σωρού ως προς τις προτεραιότητες (παρόμοιο με δομές που ονομάζονται Δένδρο Προτεραιότητας [121] και Καρτεσιανό Δένδρο [188]). Η ενδοδιάταξη σημαίνει ότι το κλειδί κάθε κόμβου είναι μεγαλύτερο από τα κλειδιά του αριστερού υποδένδρου του και μικρότερο από τα κλειδιά του δεξιού υποδένδρου του, ενώ η προτεραιότητα του είναι μεγαλύτερη από τις προτεραιότητες των κόμβων των δύο υποδένδρων του (δηλαδή είναι σωρός μεγίστων). Αν όλα τα κλειδιά, καθώς και οι προτεραιότητες, είναι διακριτά, τότε το ΔΑΣ είναι μοναδικό. Έτσι, το αντικείμενο με τη μεγαλύτερη προτεραιότητα θα είναι στην ρίζα, ενώ ο διαχωρισμός των υπόλοιπων κλειδιών στο αριστερό και δεξιό υποδένδρο θα γίνει με βάση την ενδοδιάταξη των κλειδιών.

Έστω $T$ το ΔΑΣ που αποθηκεύει το σύνολο $X$. Δοθέντος του κλειδιού ενός στοιχείου $x\in X$, το στοιχείο μπορεί να ευρεθεί στο $T$ χρησιμοποιώντας τον κλασικό αλγόριθμο σε δυαδικά δένδρα αναζήτησης. Προφανώς, ο χρόνος εύρεσης ισούται με το βάθος του κόμβου, όπου βρίσκεται το $x$ στο δένδρο $T$. Η εισαγωγή ενός νέου στοιχείου $z$ στο δένδρο $T$ επιτυγχάνεται σε δύο φάσεις. Αρχικά, με βάση την τιμή του κλειδιού του $z$ εισάγουμε το $z$ στο κατάλληλο φύλλο του $T$ και, συνεπώς, η ενδοδιάταξη του δένδρου διατηρείται. Σε μία δεύτερη φάση ελέγχεται αν ο πατέρας του $z$ έχει μικρότερη προτεραιότητα από τον $z$, διότι τότε παραβιάζεται η διάταξη σωρού. Σε μία τέτοια περίπτωση, λοιπόν, για την αποκατάσταση της διάταξης σωρού μεταφέρεται το $z$ προς τα επάνω με απλές περιστροφές.

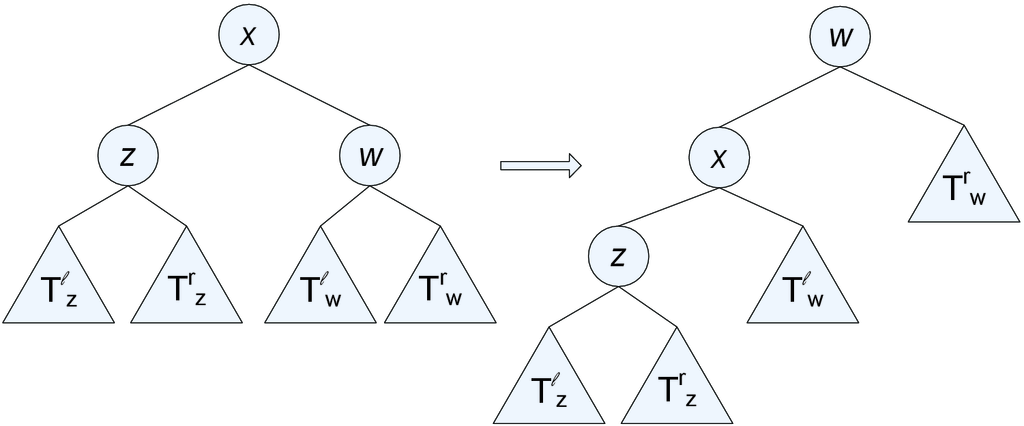
Η διαγραφή του $x$ γίνεται με αντίστοιχο τρόπο. Δηλαδή, πρώτα βρίσκουμε τον κόμβο που περιέχει το $x$ και έπειτα με απλές περιστροφές τον μεταφέρουμε προς τα κάτω μέχρι να γίνει φύλλο, ώστε να τον διαγράφουμε στη συνέχεια. Η απλή δεξιά περιστροφή ενός κόμβου $x$ με δεξιό παιδί τον $z$ και αριστερό τον $w$ και με δεξιό υποδένδρο του $z$ το $T_z^r$ και αριστερό υποδένδρο του $w$ το $T_w^{\mathrm{\ell }}$, είναι μία πράξη τοπικής μεταβολής της δομής, έτσι ώστε ο $z$ θα έχει δεξιό παιδί τον $x$ και ο $x$ αριστερό παιδί το υποδένδρο $T_z^r$. Στο Σχήμα 13.2 φαίνεται μία αριστερή περιστροφή. Προσοχή, διότι οι απλές περιστροφές γίνονται έτσι ώστε να ισχύει η διάταξη σωρού ως προς τις προτεραιότητες. Στο Σχήμα 13.3 φαίνονται επακριβώς οι πράξεις εισαγωγής και διαγραφής. Σε κάθε κόμβο του σχήματος το επάνω μέρος είναι το κλειδί (λεξικογραφική σειρά) και το κάτω μέρος είναι η προτεραιότητα.

Οι προτεραιότητες στα ΔΑΣ εισάγουν την τυχαιότητα στην κατασκευή του δένδρου. Πιο συγκεκριμένα, κάθε φορά που ένα στοιχείο με κλειδί $x$ εισάγεται στο ΔΑΣ $T$, παράγεται ένας τυχαίος αριθμός $y$ και προσάπτεται στο στοιχείο ως προτεραιότητα.

Στη συνέχεια, θα αναλύσουμε ένα σύνολο από ενδιαφέροντα μεγέθη στα ΔΑΣ, τα οποία θα μας επιτρέψουν να βρούμε τη χρονική πολυπλοκότητα των βασικών πράξεων. Αυτά τα μεγέθη είναι τα εξής:

$D(x)$:

το βάθος ενός κόμβου $x$ στο δένδρο και

$SL(x),SR(x)$:

το μήκος της δεξιάς ράχης του αριστερού υποδένδρου του $x$ και το μήκος της αριστερής ράχης του δεξιού υποδένδρου του $x$. Η αριστερή (δεξιά) ράχη ενός δένδρου είναι το μονοπάτι από τη ρίζα προς το αριστερότερο (αντιστοίχως, δεξιότερο) φύλλο.

Έστω, λοιπόν, ένα ΔΑΣ $T$ για το σύνολο $X$ με $n$ στοιχεία $x_i=(k_i,p_i)$ για $1\le i\le n$, αριθμημένα με βάση το κλειδί κατά αύξουσα τάξη. Οι προτεραιότητες $p_i$ είναι τυχαίες μεταβλητές. Αφού για καθορισμένο σύνολο κλειδιών $k_i$ η μορφή του δένδρου $T$ εξαρτάται από τις προτεραιότητες, τα προηγούμενα μεγέθη θα είναι και αυτά τυχαίες μεταβλητές και, επομένως, θα πρέπει να υπολογίσουμε μέσες τιμές. Η ανάλυση είναι πολύ απλή δεδομένου ότι κάθε ένα από τα μεγέθη αυτά μπορεί να αναπαρασταθεί με τη βοήθεια των εξής δεικνυουσών μεταβλητών:

• •

  η $A_{i,j}$ είναι 1, αν το $x_i$ είναι πρόγονος του $x_j$ στο $T$, αλλιώς είναι 0.

• •

  η $C_{i;\mathrm{\ell },m}$ είναι 1, αν το $x_i$ είναι κοινός πρόγονος των $x_{\mathrm{\ell }}$ και $x_m$, αλλιώς είναι 0.

Επίσης, θεωρούμε ότι κάθε κόμβος είναι πρόγονος του εαυτού του.

Απόδειξη.  Η (1) είναι προφανής, αφού το βάθος ενός κόμβου είναι ίσο με τον αριθμό των προγόνων του. Για τις (2) και (3) αρκεί να ασχοληθούμε με μία από τις δύο, αφού είναι συμμετρικές (έστω τη (2)).

Αν η $x_{\mathrm{\ell }}$ έχει αριστερό υποδένδρο, τότε ο χαμηλότερος κόμβος (ως προς το βάθος) στην δεξιά του υποδένδρου ράχη είναι το στοιχείο $x_{\mathrm{\ell }-1}$. Είναι σαφές ότι σε αυτή την περίπτωση η ράχη αποτελείται από όλους τους προγόνους του $x_{\mathrm{\ell }-1}$ εξαιρουμένων των προγόνων του $x_{\mathrm{\ell }}$. Όμως οι πρόγονοι του $x_{\mathrm{\ell }}$ είναι επίσης πρόγονοι του $x_{\mathrm{\ell }-1}$. Επίσης, δεν υπάρχει κάποιο $x_i$, έτσι ώστε $i\ge \mathrm{\ell }$, το οποίο να βρίσκεται επάνω σε αυτή τη ράχη. Αν η $x_{\mathrm{\ell }}$ δεν έχει αριστερό υποδένδρο, τότε είτε $\mathrm{\ell }=1$, και σε αυτή την περίπτωση η (2) σωστά δίνει $0$, ή το $x_{\mathrm{\ell }-1}$ είναι πρόγονος του $x_{\mathrm{\ell }}$ οπότε κάθε πρόγονος του $x_{\mathrm{\ell }-1}$ είναι κοινός πρόγονος των $x_{\mathrm{\ell }-1}$ και $x_{\mathrm{\ell }}$ και η (2) δίνει σωστά $0$.  

Έστω ότι $a_{i,j}$=E[$A_{i,j}$] (E υποδηλώνει μέση τιμή) και $c_{i;\mathrm{\ell },m}$ = E[$C_{i;\mathrm{\ell },m}$]. Τότε από τη γραμμικότητα της μέσης τιμής προκύπτει το εξής συμπέρασμα.

Στην ουσία η ανάλυση της πολυπλοκότητας έχει αναχθεί στην εύρεση των μέσων τιμών των $a_{i,j}$ και $c_{i;\mathrm{\ell },m}$. Αφού ασχολούμαστε με δεικνύουσες μεταβλητές έχουμε τα εξής:

$$a_{i,j}=\mathrm{E}[A_{i,j}]=Pr[A_{i,j}=1]=Pr[x_i\text{ είναι πρόγονος του }{x}_j]$$

(13.2)

$$c_{i;\mathrm{\ell },j}=\mathrm{E}[C_{i;\mathrm{\ell },j}]=Pr[C_{i;\mathrm{\ell },j}=1]=Pr[x_i\text{ είναι κοινός πρόγονος των }{x}_{\mathrm{\ell }}\text{ και }{x}_m]$$

(13.3)

Ο καθορισμός αυτών των πιθανοτήτων και κατ’ επέκταση των μέσων τιμών είναι δυνατός χρησιμοποιώντας το επόμενο λήμμα προγόνων.

Απόδειξη.  Έστω ότι $x_m$ είναι το στοιχείο με τη μεγαλύτερη προτεραιότητα στο $T$ και έστω ότι και . Από τον ορισμό του ΔΑΣ, το $x_m$ είναι η ρίζα του $T$ και τα αριστερό και δεξιό υποδένδρο της θα είναι ΔΑΣ για τα $X^{\prime }$ και $X^{\mathrm{\prime \prime }}$ αντιστοίχως.

Είναι προφανές ότι για οποιοδήποτε ζεύγος κόμβων που περιέχει τη ρίζα $x_m$ η σχέση ως προς το ποιός είναι πρόγονος είναι σωστή. Επιπλέον, η προγονική σχέση για οποιοδήποτε ζεύγος $(x_v,x_u)$, $x_v\in X^{\prime }$ και $x_u\in X^{\mathrm{\prime \prime }}$ είναι προφανής, αφού είναι σε διαφορετικά υποδένδρα και δεν έχουν κάποια σχέση μεταξύ τους. Όμως, στην περίπτωση αυτή η μέγιστη προτεραιότητα μεταξύ των $v$ και $u$ ανήκει στη ρίζα $x_m$. Το ίδιο αποδεικνύεται επαγωγικά για όλα τα ζεύγη που βρίσκονται εξ ολοκλήρου είτε στο $X^{\prime }$ είτε στο $X^{\mathrm{\prime \prime }}$.  

Μία άμεση συνέπεια αυτού του λήμματος είναι ένα ανάλογο λήμμα κοινών προγόνων.

Τα δύο τελευταία λήμματα διευκολύνουν τον υπολογισμό των πιθανοτήτων $a_{i,j}$ και $c_{i,\mathrm{\ell },m}$.

Απόδειξη.  Σύμφωνα με το λήμμα των προγόνων θα πρέπει η προτεραιότητα του $x_i$ να είναι η μεγαλύτερη ανάμεσα σε όλα τα $|i-j|+1$ στοιχεία μεταξύ των $x_i$ και $x_j$. Αφού αυτές οι προτεραιότητες είναι ανεξάρτητες και ίδιας κατανομής συνεχείς τυχαίες μεταβλητές, αυτό συμβαίνει με πιθανότητα $1/(|i-j|+1)$.  

Με αντίστοιχο τρόπο αποδεικνύεται το επόμενο συμπέρασμα.

Από τη συζήτηση που προηγήθηκε μπορούμε να υπολογίσουμε τις μέσες τιμές των μεγεθών που μας ενδιαφέρουν. Ο υπολογισμός αυτός εμπεριέχει αρμονικούς αριθμούς (δες Κεφάλαιο 2.1).

Απόδειξη.  Η απόδειξη προκύπτει με απλή αντικατάσταση των τιμών από τα Λήμματα 13.5 και 13.6 στο Λήμμα 13.2.  

Στη συνέχεια προχωρούμε στη ανάλυση των βασικών πράξεων σε ΔΑΣ. Μία επιτυχής αναζήτηση για το στοιχείο $x$ σε ένα ΔΑΣ $T$ ξεκινά από τη ρίζα του $T$ και χρησιμοποιώντας το κλειδί του $x$ ακολουθεί το μονοπάτι μέχρι τον κόμβο που περιέχει το $x$. Ο απαιτούμενος χρόνος είναι ανάλογος του μήκους του μονοπατιού ή αλλιώς του βάθους του συγκεκριμένου κόμβου που περιέχει το $x$. Επομένως, με βάση το Λήμμα 13.7 ο μέσος χρόνος για μία πράξη επιτυχούς αναζήτησης είναι O($\log n$).

Σε περίπτωση ανεπιτυχούς αναζήτησης για ένα ανύπαρκτο κλειδί μεταξύ των κλειδιών των στοιχείων $x^{-}$ και $x^{+}$, ο μέσος χρόνος είναι O($\log n$) αφού αυτή η διαδικασία θα πρέπει να σταματήσει είτε στο $x^{-}$ είτε στο $x^{+}$ (θεωρούμε ότι τα $x^{-}$ και $x^{+}$ είναι υπαρκτά).

Ένα στοιχείο εισάγεται στο ΔΑΣ, αφού πρώτα το εισάγουμε σε ένα νέο κόμβο που προσάπτεται σε ένα φύλλο που βρέθηκε κατά την ανεπιτυχή αναζήτηση. Έπειτα το στοιχείο αυτό ανεβαίνει στο μονοπάτι προς τη ρίζα με απλές περιστροφές μέχρι να μην παραβιάζεται η διάταξη σωρού. Ο αριθμός των περιστροφών είναι το πολύ ίσος με το μήκος του μονοπατιού που διασχίσθηκε κατά την ανεπιτυχή αναζήτηση. Επομένως, ο χρόνος για την εισαγωγή είναι ίσος με το χρόνο μίας ανεπιτυχούς αναζήτησης, ο οποίος στη μέση περίπτωση είναι O($\log n$).

Η πράξη της διαγραφής απαιτεί στην ουσία τον ίδιο χρόνο, αφού είναι η ακριβώς αντίστροφη διαδικασία της εισαγωγής. Κατ’αρχάς εντοπίζεται το προς διαγραφή στοιχείο με βάση το κλειδί του και έπειτα εκτελούνται απλές περιστροφές μέχρι αυτό το κλειδί να γίνει φύλλο, οπότε και το διαγράφουμε. Αν θα γίνει δεξιά ή αριστερή περιστροφή αποφασίζεται με βάση τις προτεραιότητες, αφού πάντα ο κόμβος με τη μεγαλύτερη προτεραιότητα θα περάσει προς τα επάνω.

Κάτι που είναι επίσης πολύ ενδιαφέρον είναι ο μέσος αριθμός περιστροφών ανά πράξη ενημέρωσης (εισαγωγής ή διαγραφής). Γενικώς, η περιστροφή είναι μία ακριβή πράξη σε σχέση με την προσπέλαση ενός κόμβου και θα επιθυμούσαμε το πλήθος τους να είναι κατά το δυνατόν μικρότερο. Αφού η διαγραφή είναι συμμετρική της εισαγωγής, θα μελετήσουμε μόνο την περίπτωση της διαγραφής. Έστω $x$ ένα στοιχείο του ΔΑΣ $T$, το οποίο πρόκειται να διαγραφεί. Παρότι δεν μπορούμε να συμπεράνουμε από τη δομή του $T$ ποιές περιστροφές θα εκτελεσθούν, ωστόσο μπορούμε να συμπεράνουμε πόσες θα είναι αυτές. Πιο συγκεκριμένα, το πλήθος τους θα είναι ίσο με το άθροισμα των μηκών της δεξιάς ράχης του αριστερού υποδένδρου του $x$ και της αριστερής ράχης του δεξιού υποδένδρου του $x$. Η ορθότητα του επιχειρήματος φαίνεται από το γεγονός ότι μία αριστερή περιστροφή του $x$ έχει το αποτέλεσμα της μείωσης κατά 1 του μήκους της αριστερής ράχης του δεξιού υποδένδρου, ενώ μία δεξιά περιστροφή του $x$ μειώνει το μήκος κατά 1 της δεξιάς ράχης του αριστερού υποδένδρου. Επομένως, από το Λήμμα 13.7 προκύπτει ότι ο μέσος αριθμός περιστροφών είναι μικρότερος από $2$.

Ένα φίλτρο Bloom είναι μία δομή δεδομένων που χρησιμοποιείται για να απαντήσει προσεγγιστικά ερωτήματα συμμετοχής ενός αριθμού σε ένα σύνολο αριθμών $S$. Ένα φίλτρο Bloom αποτελείται από έναν πίνακα $A$ με $m$ bits, που δεικτοδοτούνται από $\mathrm{{\rm A}}[0]$ μέχρι $\mathrm{{\rm A}}[m-1]$, όπου αρχικά $\mathrm{{\rm A}}[i]=0,0\le i\le m-1$. Το φίλτρο χρησιμοποιεί $k$ διαφορετικές συναρτήσεις κατακερματισμού στο διάστημα $[0,\mathrm{\dots },m-1]$, το οποίο αντιστοιχεί στις $m$ θέσεις του πίνακα. Υποθέτουμε ότι οι συναρτήσεις κατακερματισμού επιλέγουν κάθε κελί με ίδια πιθανότητα.

Η πρόσθεση ενός στοιχείου $y$ στο σύνολο $S$ επιτυγχάνεται εξάγοντας $k$ θέσεις στον πίνακα από τις $k$ διαφορετικές συναρτήσεις κατακερματισμού, οι οποίες εφαρμόζονται στο συγκεκριμένο στοιχείο $y$. Έπειτα, θέτουμε σε $1$ τα κελιά που δεικτοδοτούνται από αυτούς τους $k$ αριθμούς. Η ερώτηση αν ένα στοιχείο $x$ συμμετέχει στο σύνολο $S$ που ήδη έχει αποθηκευτεί σε ένα Bloom φίλτρο γίνεται εφαρμόζοντας τις $k$ συναρτήσεις κατακερματισμού στο $x$. Έπειτα ελέγχουμε τις $k$ θέσεις του πίνακα $\mathrm{{\rm A}}$ και αν όλες είναι $1$ τότε απαντάμε ότι το $x$ ανήκει στο $S$ αλλιώς, αν έστω και ένα κελί έχει $0$ τότε το στοιχείο $x$ δεν ανήκει στο $S$.

Σε περίπτωση που η απάντηση συμμετοχής του $x$ στο σύνολο $S$ είναι αρνητική, τότε το $x$ σίγουρα δεν υπάρχει στο $S$ που αποθηκεύεται στο φίλτρο Bloom. Αυτό γιατί αν είχε εισαχθεί στο φίλτρο Bloom, τότε όλες οι αντίστοιχες θέσεις του πίνακα θα ήταν $1$. Αν η απάντηση συμμετοχής είναι θετική, τότε υπάρχει η περίπτωση το στοιχείο $x$ να μην ανήκει στο $S$, αλλά όλες οι θέσεις να έχουν γίνει $1$ εξαιτίας της εισαγωγής άλλων στοιχείων στο $S$. Σε αυτή την περίπτωση έχουμε ψευδή θετική απόκριση στην ερώτηση για συμμετοχή του στοιχείου $x$.

Αν και υπάρχει η πιθανότητα ψευδούς θετικής απόκρισης, τα φίλτρα Bloom έχουν ένα εξαιρετικό πλεονέκτημα ως προς τη χρησιμοποίηση χώρου σε σχέση με άλλες δομές δεδομένων (όπως δέντρα, λίστες κοκ). Όλες αυτές οι δομές απαιτούν την αποθήκευση ολόκληρου του στοιχείου που δεικτοδοτείται, το οποίο μπορεί να είναι από μερικά bits (ακέραιος) μέχρι αρκετές εκατοντάδες ψηφιακών λέξεων (αλφαριθμητικά). Τα φίλτρα Bloom από την άλλη πλευρά με πιθανότητα ψευδούς θετικής απόκρισης $1\%$ και βέλτιστη τιμή του $k$, απαιτούν περίπου $9.6$ bits ανά στοιχείο ανεξαρτήτως μεγέθους του στοιχείου. Γενικά την πιθανότητα ψευδούς θετικής απόκρισης μπορούμε να την υποδεκαπλασιάζουμε απλώς αυξάνοντας το χώρο ανά στοιχείο κατά $4.8$ bits. Επιπλέον, το κόστος για ένθεση ενός στοιχείου είναι συνάρτηση μόνο του $k$ και όχι του μεγέθους του στοιχείου ή του μεγέθους του συνόλου. Όμως, ένα σημαντικό πρόβλημα που έχουν τα φίλτρα Bloom είναι ότι είναι δύσκολο να υποστηριχθεί η διαγραφή ενός στοιχείου.

Απόδειξη.  Έστω ότι η συνάρτηση κατακερματισμού επιλέγει κάθε θέση του πίνακα με ίδια πιθανότητα. Αν $m$ είναι ο αριθμός των bits στον πίνακα $A$, η πιθανότητα ότι κάποιο συγκεκριμένο bit δεν θα γίνει ίσο με $1$ κατά την εισαγωγή ενός στοιχείου είναι:

$$1-\frac{1}{m}$$

Η πιθανότητα ότι δεν θα τεθεί από καμία από τις $k$ συναρτήσεις κατακερματισμού θα είναι:

$${\left(1-\frac{1}{m}\right)}^k$$

Αν ενθέσουμε $n$ στοιχεία, τότε η πιθανότητα να είναι $0$ είναι:

$${\left(1-\frac{1}{m}\right)}^{kn}\approx e^{-kn/m}$$

και, άρα, η πιθανότητα αυτό να είναι $1$ είναι:

$$1-{\left(1-\frac{1}{m}\right)}^{kn}\approx 1-e^{-kn/m}$$

Έστω ότι ελέγχουμε την συμμετοχή στο $S$ ενός στοιχείου $x$ που δεν ανήκει σε αυτό. Τότε η πιθανότητα να έχουμε ψευδή θετική απόκριση είναι:

$${\left(1-e^{-kn/m}\right)}^k$$

Έστω ότι $f={\left(1-e^{-kn/m}\right)}^k$. Η πιθανότητα ψευδούς θετικής απόκρισης μειώνεται, όταν αυξάνεται το $m$ και αυξάνεται καθώς το $n$ αυξάνει. Για δοσμένα $m$ και $n$, η τιμή του $k$ που ελαχιστοποιεί αυτή την πιθανότητα προκύπτει από την ελαχιστοποίηση της συνάρτησης $g=k\ln (1-e^{kn/m})$, ενώ ισχύει ότι $f=e^g$. Άρα, η καλύτερη τιμή για το $k$ προκύπτει από την ελαχιστοποίηση της $g$ ως προς $k$. Παίρνοντας την πρώτη παράγωγο της $g$ ως προς $k$ βρίσκουμε ότι η συνάρτηση ελαχιστοποιείται για $k=\ln 2\frac{m}{n}$. Αντικαθιστώντας το $k$ βρίσκουμε την πιθανότητα ψευδούς απόκρισης:

$${\left(1-e^{-\ln 2m/n\cdot n/m}\right)}^{\ln 2m/n}={\left(\frac{1}{2}\right)}^{\ln 2m/n}\approx {0.6185}^{m/n}$$

 

Η μέθοδος των λιστών παράλειψης (skip lists) προτάθηκε από τον Pugh το 1990. Η δομή αυτή είναι πολύ αποτελεσματική σε όλες τις σχετικές λειτουργίες, δηλαδή αναζήτηση, εισαγωγή και διαγραφή. Για την επεξήγηση της δομής πρέπει να γίνει μία μικρή εισαγωγή με ένα παράδειγμα.

Ας θεωρηθεί κατ’αρχάς μία κλασική απλή λίστα που περιέχει ταξινομημένα κλειδιά, όπως φαίνεται στην πρώτη δομή του επόμενου σχήματος. Είναι γνωστό ότι στη χειρότερη περίπτωση για μία επιτυχή αναζήτηση θα διασχισθεί η λίστα μέχρι τέλους. Στη δεύτερη δομή του σχήματος κάθε δεύτερος κόμβος της λίστας περιέχει δύο δείκτες αντί ένα: ο πρώτος δείκτης δείχνει στον επόμενο κόμβο, ενώ ο δεύτερος δείχνει στο μεθεπόμενο κόμβο της λίστας. Φαίνεται διαισθητικά ότι στη χειρότερη περίπτωση για μία επιτυχή αναζήτηση θα προσπελασθούν $\lceil n/2\rceil +1$ κόμβοι, όπου $n$ είναι το μήκος της λίστας. Κατά παρόμοιο τρόπο στην τρίτη δομή του σχήματος, όπου κάθε τέταρτος κόμβος περιέχει τέσσερις δείκτες, μία επιτυχής αναζήτηση θα απαιτήσει στη χειρότερη περίπτωση την προσπέλαση $\lceil n/4\rceil +2$ κόμβων της λίστας.

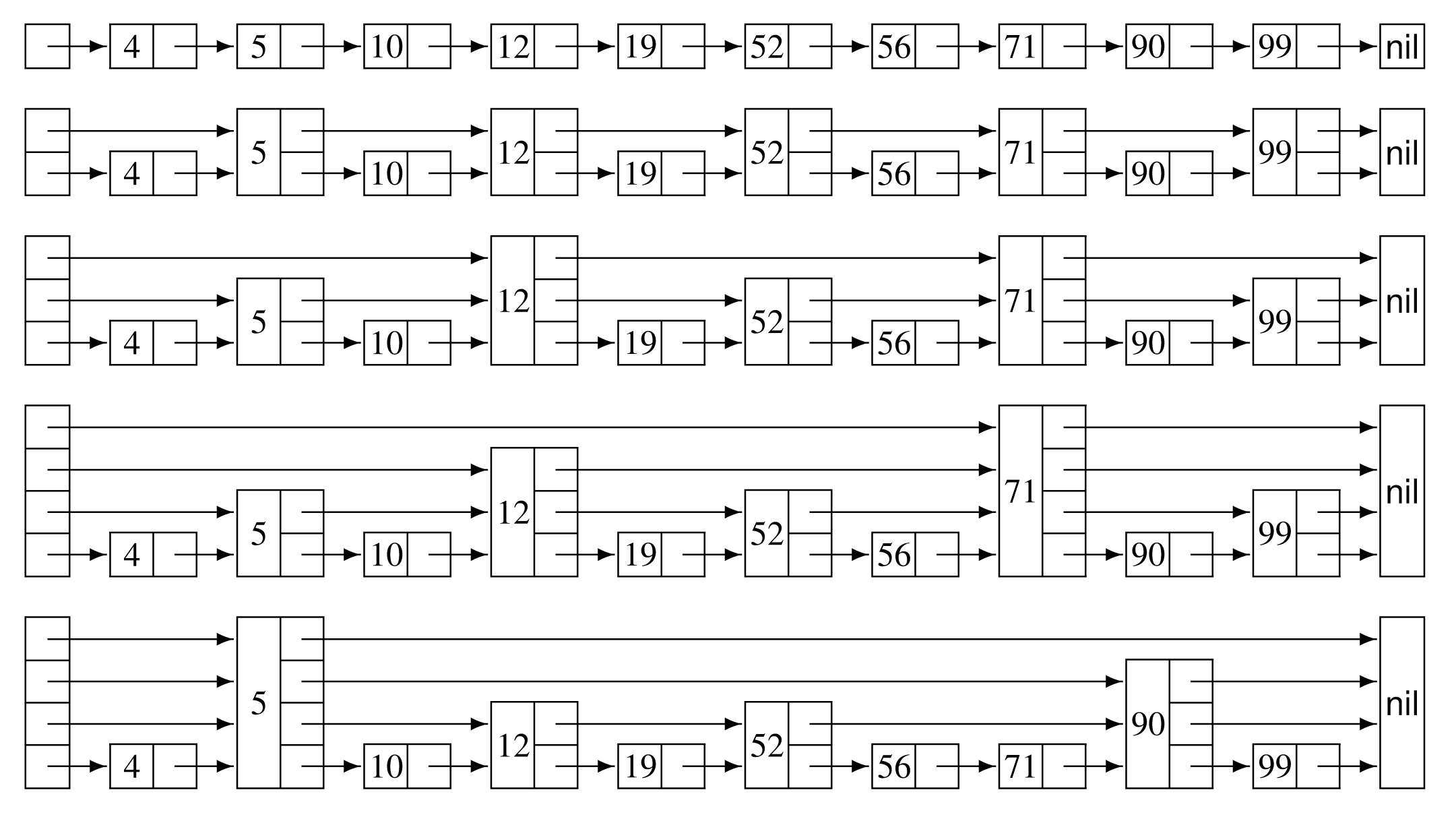
Στην τέταρτη δομή του σχήματος υπάρχουν κόμβοι με ένα δείκτη σε ποσοστό 50%, κόμβοι με δύο δείκτες σε ποσοστό 25%, κόμβοι με τρεις δείκτες σε ποσοστό 12,5% και, τέλος, κόμβοι με τέσσερις δείκτες σε ποσοστό 12,5%. Λέγεται ότι ο κόμβος με $i$ δείκτες βρίσκεται στο $i$-οστό επίπεδο (level). Ακολουθώντας το σκεπτικό αυτό είναι πλέον ευνόητο τι κατανομή κόμβων υπάρχει σε μία λίστα με κόμβους μέχρι $i$ επίπεδα.

Σε μία λίστα παράλειψης με κόμβους σε $i$ επίπεδα η κατανομή των κόμβων ακολουθεί τη μέθοδο αυτή, αλλά η αλληλουχία τους είναι τυχαία. Δείγμα δομής λιστών παράλειψης είναι η τελευταία περίπτωση του προηγούμενου σχήματος. Στη δομή αυτή ένας πίνακας δεικτών παίζει το ρόλο του δείκτη header των κλασικών συνδεδεμένων λιστών. Όλοι οι δείκτες αρχικοποιούνται με τιμή nil. Η αναζήτηση ενός κλειδιού σε μία τέτοια δομή γίνεται αρχικά ακολουθώντας την αλυσίδα των δεικτών του μεγαλυτέρου επιπέδου, μέχρι να προσπελασθεί κόμβος με κλειδί ίσο ή μεγαλύτερο από το αναζητούμενο. Στην πρώτη περίπτωση η διαδικασία τερματίζεται, ενώ στη δεύτερη η διαδικασία συνεχίζεται ακολουθώντας την αλυσίδα των δεικτών του χαμηλότερου επιπέδου. Έτσι, η διαδικασία συνεχίζεται διαδοχικά θεωρώντας τις αλυσίδες των μικρότερων επιπέδων. Για παράδειγμα, κατά την αναζήτηση του κλειδιού 71 στην τελική δομή του σχήματος προσπελάζονται οι κόμβοι με κλειδιά 5, 90, 12, 52, 56 και τελικά 71.

Η επόμενη διαδικασία search περιγράφει την αναζήτηση σε μία λίστα παράλειψης του κλειδιού searchkey. Με τη μεταβλητή level συμβολίζεται το μέγιστο επίπεδο της λίστας παράλειψης, ενώ με forward συμβολίζονται οι δείκτες των διαδοχικών επιπέδων.

     procedure search(searchkey)
1.   x <-- header
2.   for  i <-- level downto 1 do
3.      while x.forward[i].key < searchkey
4.         do x <-- x.forward[i]
5.   x <-- x.forward[1]
6.   if x.key=searchkey then print(successful)
7.   else print(unsuccessful)

Η διαδικασία εισαγωγής ενός κλειδιού αρχίζει σαν τη διαδικασία της αναζήτησης, ώστε να εντοπισθεί το σημείο, όπου θα πρέπει να δημιουργηθεί ο νέος κόμβος. Ο αριθμός των δεικτών του νέου κόμβου προσδιορίζεται με ένα ψευδοτυχαίο αριθμό που υπακούει την κατανομή των κόμβων ανά επίπεδο. Για την ολοκλήρωση της διαδικασίας απαιτείται η σύνδεση του νέου κόμβου με τους υπόλοιπους της δομής. Αυτό επιτυγχάνεται με τη χρήση ενός βοηθητικού πίνακα που περιέχει τους δεξιότερους δείκτες όλων των επιπέδων που βρίσκονται αριστερά από το σημείο όπου θα γίνει η εισαγωγή. Ανάλογη διαχείριση απαιτείται και κατά τη διαγραφή ενός κόμβου, ώστε να γίνει η σύνδεση των κόμβων της λίστας. Κατά την υλοποίηση απαιτείται κάποια προσοχή στη διαχείριση των δεικτών επειδή η εισαγωγή ή η διαγραφή μπορεί να αφορά σε κόμβο οποιουδήποτε επιπέδου. Η επόμενη διαδικασία insert αποτυπώνει αυτήν την περιγραφή. Ο πίνακας update χρειάζεται για τη σύνδεση των κόμβων της δομής. Πιο συγκεκριμένα, στη θέση update[i] τοποθετείται ο κατάλληλος δείκτης προς το δεξιότερο κόμβο επιπέδου $i$ ή υψηλότερου, ο οποίος κόμβος βρίσκεται στα αριστερά του σημείου όπου θα εισαχθεί ο νέος κόμβος μέσω της makenode. Οι μεταβλητές value και newvalue αναφέρονται σε ένα βοηθητικό πεδίο.

     procedure insert(searchkey,newvalue)
1.   x <-- header
2.   for  <-- level downto 1 do
3.      while x.forward[i].key < searchkey
4.         do x <-- x.forward[i]
5.      update[i] <-- x
6.   x <-- x.forward[1]
7.   if x.key=searchkey then x.value <-- newvalue
8.   else
9.      newlevel <-- randomlevel
10.     if newlevel>level then
11.        for i <-- level+1 to newlevel do
12.           update[i] <-- header
13.        level <-- newlevel
14.     x <-- makenode(newlevel,searchkey,value)
15.     for i <-- 1 to newlevel do
16.        x.forward[i] <-- update[i].forward[i]
17         update[i].forward[i] <-- x

Στην πρώτη δομή του επόμενου σχήματος παρουσιάζεται η διαδικασία αναζήτησης της θέσης όπου θα πρέπει να εισαχθεί το κλειδί 52, ενώ στο κάτω μέρος του σχήματος δίνεται η τελική κατάσταση της δομής.

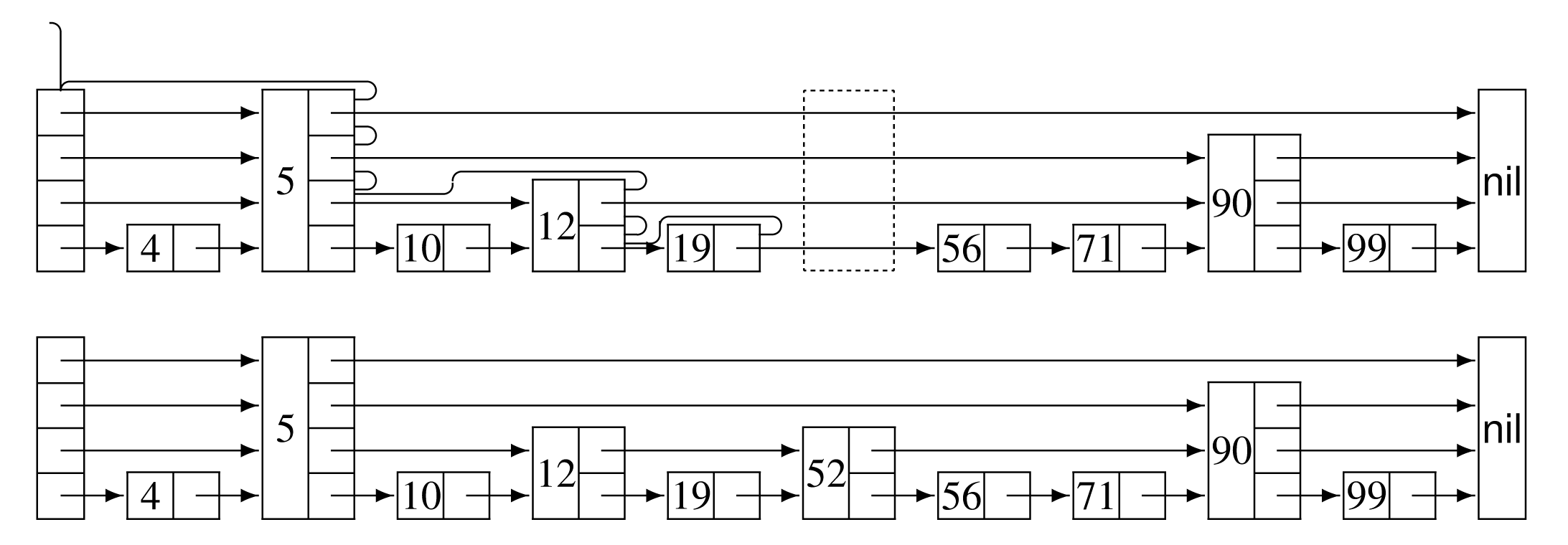
Στη διαδικασία insert σημαντικό ρόλο παίζει η διαδικασία randomlevel, που με μια λογική Las Vegas προσδιορίζει με τυχαίο τρόπο το επίπεδο του προς εισαγωγή κόμβου. Η διαδικασία randomlevel που δίνεται στη συνέχεια είναι γενική, καθώς με p συμβολίζεται το ποσοστό των κόμβων με δείκτες στο $i$-οστό επίπεδο, οι οποίοι έχουν δείκτες και στο ($i+1$)-οστό επίπεδο.

     procedure randomlevel
1.   newlevel <-- 1
2.   while random()<p do newlevel <-- newlevel+1
3.   return min(newlevel,maxlevel)

Για $p=1/2$, η διαδικασία μοιάζει με τη συνεχή ρίψη κερμάτων μέχρι να έρθουν “γράμματα”. Η πιθανότητα ένα δεδομένο στοιχείο να αποθηκευθεί σε κόμβο του $i$-οστού επιπέδου είναι ίση με την πιθανότητα ρίχνοντας το κέρμα να βγάλουμε $i-1$ φορές “κορώνα” και κατόπιν “γράμματα”. Αυτό μπορεί να συμβεί με πιθανότητα $1/2^i$. Η πιθανότητα ένα στοιχείο να ξεπεράσει τα $c\log n$ επίπεδα είναι $1/2^{c\log n}=1/n^c$. Άρα, η πιθανότητα οποιοδήποτε στοιχείο να βρίσκεται σε παραπάνω από $c\log n$ επίπεδα δε θα είναι μεγαλύτερη από $1/n^{c-1}$. Για παράδειγμα, το ύψος $h$ είναι μεγαλύτερο από $3\log n$ με πιθανότητα:

$$\frac{1}{n^2}$$

(13.6)

Γενικώς, δοθείσης σταθεράς $c>1$, το ύψος $h$ είναι μεγαλύτερο από $c\log n$ με πιθανότητα το πολύ $1/n^{c-1}$. Συνεπώς, με πολύ μεγάλη πιθανότητα το ύψος είναι Ο($\log n$). Ωστόσο, θεωρητικά η τιμή του ύψους μπορεί να γίνει οσοδήποτε μεγάλη. Για το λόγο αυτό αποφασίζεται από την αρχή η μέγιστη τιμή του επιτρεπτού πλήθους επιπέδων maxlevel να ισούται με ${\log }_{1/p}n=\frac{1}{\log 1/p}\log n$, και, άρα, $c=\frac{1}{\log 1/p}$, $p>2$.

Στη συνέχεια, θα ασχοληθούμε με την ανάλυση της πολυπλοκότητας της διαδικασίας της αναζήτησης. Η πολυπλοκότητα της διαδικασίας της εισαγωγής και της διαγραφής είναι παρόμοια, καθώς το επιπλέον κόστος είναι συνάρτηση του μέγιστου αριθμού των επιπέδων και όχι του πλήθους των στοιχείων της δομής. Για τους σκοπούς της ανάλυσης αυτής θα μελετήσουμε τα βήματα της αναζήτησης κατά την αντίστροφη φορά. Για παράδειγμα, έστω ότι στο Σχήμα 13.5 αναζητούμε το κλειδί 56. Ο Πίνακας 13.2 δείχνει τις εκτελούμενες ενέργειες κατά την αντίστροφη φορά.

Πρόταση.
Η πολυπλοκότητα της αναζήτησης σε λίστα παράλειψης είναι λογαριθμική.

Απόδειξη
Η πολυπλοκότητα της αναζήτησης εξαρτάται από τον αριθμό των βημάτων προς τα επάνω και προς τα πίσω. Εκ κατασκευής η πιθανότητα από κάποιο σημείο να κινηθούμε προς τα πίσω είναι $1-p$, ενώ η πιθανότητα να κινηθούμε προς τα επάνω είναι $p$. Έστω ότι με $C(k)$ συμβολίζουμε τη μέση τιμή του μήκους του μονοπατιού αναζήτησης που ανεβαίνει $k$ επίπεδα σε μία δομή με άπειρα επίπεδα. Ως αρχική συνθήκη ισχύει $C(0)=0$ και γενικώς:

	$C(k)$	$=$	$(1-p)(1+C(k))+p(1+C(k-1))$
		$=$	$1/p+C(k-1)=k/p$

Με απλά λόγια, ένα μονοπάτι που ανεβαίνει $k$ επίπεδα έχει μήκος $2k$ για $p=1/2$. Ο μέγιστος αριθμός επιπέδων είναι $\log n$. Επομένως, η δομή έχει λογαριθμική πολυπλοκότητα Ο($\log n$). $\mathrm{\square }$  

Πρόταση.
Η χωρική πολυπλοκότητα της λίστας παράλειψης είναι γραμμική.

Απόδειξη
Ως προς τη χωρική πολυπλοκότητα παρατηρούμε τα εξής υποθέτοντας ότι $p=1/2$. Με το προηγούμενο σκεπτικό γνωρίζουμε ότι η πιθανότητα ένα στοιχείο να βρίσκεται στο $i$-οστό επίπεδο είναι ίση με την πιθανότητα ρίχνοντας το κέρμα να βγάλουμε $i-1$ φορές “κορώνα” και κατόπιν “γράμματα”. Αυτό μπορεί να συμβεί με πιθανότητα $1/2^i$. Επομένως, η μέση τιμή των στοιχείων στο $i$-οστό επίπεδο είναι $n/2^i$. Άρα, η προσδοκητή τιμή του πλήθους των δεικτών είναι:

$$\sum _{i=0}^h\frac{n}{2^i}=n\sum _{i=1}^h\frac{1}{2^i}=n\frac{1-{(\frac{1}{2})}^{h+1}}{1-\frac{1}{2}}=n\left(2-{(1/2)}^h\right)$$

(13.7)

όπου $h={\log }_{1/p}n$ είναι ο αριθμός των επιπέδων της δομής. Συνεπώς, ασυμπτωτικά προκύπτει ότι η χωρική πολυπλοκότητα είναι Θ($n$). $\mathrm{\square }$

Μελετήσαμε τη γρήγορη ταξινόμηση στο Κεφάλαιο 8.3. Η επίδοση της γρήγορης ταξινόμησης εξαρτάται από την επιλογή του άξονα (pivot). Στη κλασική έκδοση του αλγορίθμου ως άξονας επιλέγεται το πρώτο στοιχείο του πίνακα. Αν η τιμή του άξονα είναι το μεσαίο στοιχείο του τελικώς ταξινομημένου πίνακα, τότε ο αρχικός πίνακας χωρίζεται σε δύο ίσους υποπίνακες. Σε αντίθεση με αυτή την καλύτερη περίπτωση, στη χειρότερη περίπτωση η τιμή του άξονα μπορεί να είναι η μικρότερη ή η μεγαλύτερη τιμή των στοιχείων του πίνακα, οπότε ο πίνακας θα υποδιαιρεθεί σε δύο υποπίνακες μεγέθους 0 και $n-1$.

Στη βιβλιογραφία έχουν προταθεί αρκετές παραλλαγές της γρήγορης ταξινόμησης με σκοπό την επιλογή ενός άξονα με τιμή που να οδηγεί σε καλύτερο διαμερισμό. Μία παραλλαγή είναι η λεγόμενη “μεσαίος των τριών”(median-of-three), όπου από το πρώτο, το τελευταίο και το μεσαίο στοιχείο του πίνακα επιλέγεται ως άξονας το στοιχείο με τη μεσαία τιμή μεταξύ των τριών. Μία άλλη παραλλαγή είναι η ταξινόμηση με τη μέση τιμή (meansort), όπου ως άξονας επιλέγεται η μέση τιμή των στοιχείων του πίνακα. Έχει αποδειχθεί ότι στη χειρότερη περίπτωση οι τεχνικές αυτές δεν αποφεύγουν την τετραγωνική πολυπλοκότητα Θ($n^2$).

Σκοπός μας, λοιπόν, είναι ένας “δίκαιος” (δηλαδή αποτελεσματικός) διαμερισμός. Για το σκοπό αυτό προτείνεται η επιλογή ενός τυχαίου στοιχείου του πίνακα ως άξονα. Η επόμενη διαδικασία σκιαγραφεί την τεχνική αυτή τύπου Las Vegas.

     procedure quicksortrand(left,right);
1.   if left<right then
2.      i <-- left; j <-- right+1;
3.      k <-- random(left,right);
4.      swap(A[k],A[left]); pivot <-- A[left];
5.      repeat
6.         repeat i <-- i+1 until A[i]>=pivot;
7.         repeat j <-- j-1 until A[j]<=pivot;
8.         if i<j then swap(A[i],A[j]);
9.      until j<=i;
10.     swap(A[left],A[j]);
11.     quicksort(left,j-1);
12.     quicksort(j+1,right)

Στη συνέχεια, θα προχωρήσουμε στην παρουσίαση δύο ανεξάρτητων αλλά ισοδύναμων αποδείξεων σχετικά με την πολυπλοκότητα της τυχαίας γρήγορης ταξινόμησης. Η πρώτη έχει ως εξής:

Πρόταση.
Η πολυπλοκότητα της γρήγορης ταξινόμησης είναι Θ($n\log n$) στη μέση περίπτωση.

Απόδειξη 1η
Δεδομένου ενός συνόλου $S$, με $S_i$ συμβολίζουμε τον $i$-οστό μικρότερο αριθμό. Ορίζουμε την τυχαία μεταβλητή $X_{ij}$, ώστε να έχει τιμή 1 (0) αν τα στοιχεία $S_i$ και $S_j$ (δεν) συγκριθούν κατά την εκτέλεση της τυχαίας γρήγορης ταξινόμησης. Συνεπώς, για την προσδοκητή τιμή του συνολικού αριθμού συγκρίσεων που εκτελούνται από τον αλγόριθμο ισχύει:

$$\mathrm{E}\left[\sum _{i=1}^{n-1}\sum _{j\ge i}{X}_{ij}\right]=\sum _{i=1}^{n-1}\sum _{j\ge i}\mathrm{E}[X_{ij}]$$

(13.8)

Καθώς η τυχαία μεταβλητή παίρνει τιμές 0 και 1, ουσιαστικά δηλώνει την πιθανότητα τα στοιχεία $S_i$ και $S_j$ να συγκριθούν. Έστω τα στοιχεία $S_i,S_{i+1},\mathrm{\dots },S_j$. Τα δύο στοιχεία $S_i$ και $S_j$ θα συγκριθούν, αν το ένα από τα δύο έχει επιλεγεί ως άξονας. Αν δεν έχει επιλεγεί το ένα από τα δύο ως άξονας, τότε θα έχει επιλεγεί ένα εκ των $S_{i+1},\mathrm{\dots },S_{j-1}$, γεγονός που θα στείλει τα δύο στοιχεία $S_i$ και $S_j$ σε διαφορετικούς υποπίνακες, οπότε δεν πρόκειται να συγκριθούν. Συνεπώς, η πιθανότητα τα δύο αυτά στοιχεία να συγκριθούν είναι $2/(j-i+1)$. Άρα:

	${\displaystyle \sum _{i=1}^{n-1}}{\displaystyle \sum _{j\ge i}}\mathrm{E}[X_{ij}]$	$=$	${\displaystyle \sum _{i=1}^{n-1}}{\displaystyle \sum _{j=i+1}^n}{\displaystyle \frac{2}{j-i+1}}={\displaystyle \sum _{i=1}^{n-1}}{\displaystyle \sum _{k=1}^{n-i}}{\displaystyle \frac{2}{k+1}}$
			${\displaystyle \sum _{i=1}^{n-1}}{\displaystyle \sum _{k=1}^{n-i}}{\displaystyle \frac{2}{k}}={\displaystyle \sum _{i=1}^{n-1}}\mathrm{O}(\log n)=\mathrm{O}(n\log n)$

$\mathrm{\square }$

Απόδειξη 2η
Η δεύτερη εναλλακτική απόδειξη στηρίζεται στις αναδρομικές εξισώσεις και τον ορισμό της πολυπλοκότητας. Για την ανάλυσή μας, για τη θέση $j$ του pivot θα θεωρήσουμε δύο ισοπίθανες περιπτώσεις (δηλαδή πιθανότητα 1/2):

• •

  τον “καλό διαμερισμό” όπου ισχύει:

  $$left+\frac{right-left+1}{4}\le j\le right-\frac{right-left+1}{4}$$

  (13.9)

• •

  τον “κακό διαμερισμό” όπου ισχύει:

  (13.10)

  ή

  $$right>j\ge right-\frac{right-left+1}{4}$$

  (13.11)

Με απλά λόγια, καλός θεωρείται ο διαχωρισμός όταν ο τυχαία επιλεγόμενος άξονας οδηγεί σε διαμερισμό όπου ο μικρότερος υποπίνακας έχει μέγεθος το ελάχιστο $(right-left+1)/4$, ενώ ο μεγαλύτερος υποπίνακας έχει μέγεθος το πολύ $3(right-left+1)/4$.

Από το Κεφάλαιο 8.3 γνωρίζουμε ότι γενικώς ισχύει η επόμενη αναδρομική εξίσωση για $n\ge 2$:

$$T(n)=n+\frac{1}{n}\sum _{k=0}^{n-1}\left(T(k)+T(n-k-1)\right)$$

(13.12)

Αν με κάποιο τρόπο μπορούσαμε να εγγυηθούμε ότι κάθε διαμερισμός θα είναι καλός, τότε θα ίσχυε η επόμενη αναδρομική εξίσωση:

	$T_g(n)$	$=$	$n+{\displaystyle \frac{2}{n}}{\displaystyle \sum _{k=n/4}^{3n/4-1}}\left(T_g(k)+T_g(n-k-1)\right)$
		$=$	$n+{\displaystyle \frac{4}{n}}{\displaystyle \sum _{k=n/4}^{n/2-1}}\left(T_g(k)+T_g(n-k-1)\right)$
		$\le$	$n+{\displaystyle \frac{4}{n}}{\displaystyle \sum _{k=n/4}^{n/2-1}}\left(T_g(3n/4)+T_g(n/4)\right)$
		$=$	$n+{\displaystyle \frac{4}{n}}\mathit{\hspace{1em}}(n/2-n/4)\mathit{\hspace{1em}}\left(T_g(3n/4)+T_g(n/4)\right)$
		$=$	$n+T_g(3n/4)+T_g(n/4)$

Στην ανωτέρω επεξεργασία χρησιμοποιήσαμε το γεγονός ότι η μέγιστη τιμή της ποσότητας $T_g(k)+T_g(n-k+1)$ στο διάστημα $n/4\le j\le 3n/4-1$ λαμβάνεται στα άκρα του διαστήματος¹²¹²Για λόγους ευκολίας τα όρια του αθροίσματος δεν ταυτίζονται με τα όρια που προσδιορίσθηκαν προηγουμένως στις περιπτώσεις του καλού και του κακού διαχωρισμού..

Τώρα θέλουμε να αποδείξουμε ότι $T_g(n)\le cn\log n$. Θα το αποδείξουμε με επαγωγή. Η αλήθεια της πρότασης ισχύει για μικρά $n$ και για . Θα αποδείξουμε ότι ισχύει και για κάθε $n$. Διαδοχικά έχουμε:

	$T_g(n)$	$\le$	$n+T_g(3n/4)+T_g(n/4)$
		$\le$	$n+c{\displaystyle \frac{3n}{4}}\log {\displaystyle \frac{3n}{4}}+c{\displaystyle \frac{n}{4}}\log {\displaystyle \frac{n}{4}}=n+{\displaystyle \frac{cn}{4}}\left(3\log {\displaystyle \frac{3n}{4}}+\log {\displaystyle \frac{n}{4}}\right)$
		$=$	$n+{\displaystyle \frac{cn}{4}}\left(3\log n+3\log 3-3\log 4+\log n-\log 4\right)$
		$=$	$n+{\displaystyle \frac{cn}{4}}\left(4\log n+3\log 3-8\right)=cn\log n-n\left(2c-1-{\displaystyle \frac{3c\log 3}{4}}\right)$
		$=$	$cn\log n-n\left(0.81c-1\right)\le cn\log n$

όπου η αλήθεια της τελευταίας ανισοϊσότητας προκύπτει για $c\ge 2$.  

Από την άλλη πλευρά υπάρχει και ο κακός διαμερισμός για τον οποίο ισχύει:

	$T_b(n)$	$=$	$n+{\displaystyle \frac{4}{n}}{\displaystyle \sum _{k=3n/4}^{n-1}}\left(T_b(k)+T_b(n-k-1)\right)$
		$\le$	$n+{\displaystyle \frac{4}{n}}{\displaystyle \sum _{k=3n/4}^{n-1}}\left(T_b(n-1)+T_b(0)\right)$
		$=$	$n+{\displaystyle \frac{4}{n}}{\displaystyle \sum _{k=3n/4}^{n-1}}{T}_b(n-1)=n+T_b(n-1)$

Από την τελευταία σχέση καταλήγουμε ότι: $T_b(n)=\mathrm{\Theta }(n^2)$. Όμως, με την όποια πιθανότητα θα συμβεί ένας κακός διαμερισμός με την ίδια πιθανότητα θα συμβεί και ένας καλός διαμερισμός. Άρα, στη γενική περίπτωση ισχύει:

	$T(n)$	$=$	$n+{\displaystyle \frac{1}{n}}{\displaystyle \sum _{k=0}^{n-1}}\left(T(k)+T(n-k-1)\right)$
		$=$	$n+{\displaystyle \frac{2}{n}}{\displaystyle \sum _{k=n/2}^{n-1}}\left(T(k)+T(n-k-1)\right)$
		$=$	$n+{\displaystyle \frac{2}{n}}{\displaystyle \sum _{k=n/2}^{3n/4-1}}\left(T(k)+T(n-k-1)\right)+{\displaystyle \frac{2}{n}}{\displaystyle \sum _{k=3n/4}^{n-1}}\left(T(k)+T(n-k-1)\right)$
		$\le$	$n+{\displaystyle \frac{2}{n}}{\displaystyle \sum _{k=n/2}^{3n/4-1}}\left(T(3n/4)+T(n/4)\right)+{\displaystyle \frac{2}{n}}{\displaystyle \sum _{k=3n/4}^{n-1}}\left(T(n-1)+T(0)\right)$
		$\le$	$n+{\displaystyle \frac{2}{n}}{\displaystyle \frac{n}{4}}\left(T(3n/4)+T(n/4)\right)+{\displaystyle \frac{2}{n}}{\displaystyle \frac{n}{4}}T(n-1)$
		$=$	$n+{\displaystyle \frac{1}{2}}\left(T(3n/4)+T(n/4)+T(n-1)\right)$

Όπως και πριν, θα αποδείξουμε επαγωγικά ότι $T(n)\le cn\log n$ για κάποια σταθερά $c$. Η αλήθεια της πρότασης ισχύει για μικρά $n$ και για . Θα αποδείξουμε ότι ισχύει και για $n$. Διαδοχικά έχουμε:

	$T(n)$	$\le$	$n+{\displaystyle \frac{1}{2}}\left(T(3n/4)+T(n/4)+T(n-1)\right)$
		$\le$	$n+{\displaystyle \frac{1}{2}}\left(c{\displaystyle \frac{3n}{4}}\log {\displaystyle \frac{3n}{4}}+c{\displaystyle \frac{n}{4}}\log {\displaystyle \frac{n}{4}}+c(n-1)\log (n-1)\right)$
		$=$	$n+\left({\displaystyle \frac{3cn}{8}}\log n+{\displaystyle \frac{3cn}{8}}\log {\displaystyle \frac{3}{4}}+{\displaystyle \frac{cn}{8}}\log n+{\displaystyle \frac{cn}{8}}\log {\displaystyle \frac{1}{4}}+{\displaystyle \frac{c(n-1)}{2}}\log (n-1)\right)$
		$=$	$n+\left({\displaystyle \frac{cn}{2}}\log n-cn+{\displaystyle \frac{3cn\log 3}{8}}+{\displaystyle \frac{c(n-1)}{2}}\log (n-1)\right)$
		$\le$	$n+\left({\displaystyle \frac{cn}{2}}\log n-cn+{\displaystyle \frac{3cn\log 3}{8}}+{\displaystyle \frac{cn}{2}}\log n\right)$
		$=$	$cn\log n-n\left(0.41c-1\right)\le cn\log n$

όπου η αλήθεια της τελευταίας ανισοϊσότητας προκύπτει για $c\ge 3$. $\mathrm{\square }$  

Διαπιστώνουμε, λοιπόν, ότι και πάλι καταλήγουμε στο ίδιο συμπέρασμα σε σχέση με την επίδοση της μέσης περίπτωσης. Ωστόσο, ενώ στην ανάλυση της κλασικής γρήγορης ταξινόμησης θεωρούμε το σύνολο των διαφορετικών διατάξεων που μπορούν να εισαχθούν προς ταξινόμηση, στην παρούσα περίπτωση θεωρούμε το σύνολο των δυνατών αποτελεσμάτων της τυχαίας γεννήτριας. Στη συμβατική γρήγορη ταξινόμηση μπορούσαμε να ισχυρισθούμε ότι: Αν τα δεδομένα είναι τυχαία, τότε η πολυπλοκότητα της μέσης περίπτωσης της γρήγορης ταξινόμησης είναι Θ($n\log n$)’. Αντίθετα τώρα μπορούμε να ισχυρισθούμε ότι: “Με πολύ μεγάλη πιθανότητα η τυχαία γρήγορη ταξινόμηση εκτελείται σε χρόνο Θ($n\log n$)”.

Όπως γνωρίζουμε από την Άσκηση 1.12, πρώτος λέγεται ένας ακέραιος αριθμός, αν διαιρείται μόνο από τη μονάδα και τον εαυτό του. Το 1 δεν θεωρείται πρώτος, ενώ οι 5 μικρότεροι αριθμοί είναι οι 2, 3, 5, 7 και 11. Εκτός από τους αρχαίους Έλληνες (όπως ο Ευκλείδης και ο Ερατοσθένης), με το πρόβλημα είχαν ασχοληθεί και οι αρχαίοι Κινέζοι που πίστευαν ότι αν ο αριθμός $2^n-2$ διαρείται ακριβώς δια του $n$, τότε ο $n$ είναι πρώτος. Ωστόσο, η εικασία αυτή δεν είναι ορθή. Αντιπαράδειγμα αποτελεί ο αριθμός $n=341$. Το πρόβλημα του ελέγχου αν ένας αριθμός είναι πρώτος ή σύνθετος (primality testing), καθώς και το πρόβλημα της παραγοντοποίησης (factorization) βρίσκουν σημαντική χρήση στην κρυπτογραφία, μία γνωστική περιοχή που βασίζεται στο γεγονός ότι δεν υπάρχουν αποτελεσματικοί αλγόριθμοι για την παραγοντοποίηση μεγάλων αριθμών.  

Σύμφωνα με την Άσκηση 1.12, αν $n$ είναι ένας θετικός σύνθετος ακέραιος, τότε ο $n$ έχει έναν πρώτο αριθμό που δεν ξεπερνά το $\sqrt{n}$. Επομένως, προκειμένου να διαπιστώσουμε αν ένας ακέραιος $n$ είναι πρώτος αρκεί να εκτελέσουμε $\sqrt{n}$ δοκιμές στη χειρότερη περίπτωση και να απαντήσουμε με βεβαιότητα κατά πόσο ο αριθμός είναι πρώτος. Στην επόμενη διαδικασία prime1 υποθέτουμε ότι ο n είναι περιττός αριθμός.

     procedure prime1(n)
1.   for i <-- 3 to n step 2 do
2.      if n mod i = 0 then return false;
3.   return true

Λέγεται ότι ένας αλγόριθμος είναι αποτελεσματικός χρονο-πολυωνυμικά (poly-time efficient) αν εκτελείται σε χρόνο πολυωνυμικό ως προς το μήκος του μεγέθους της αναπαράστασης του αριθμού σε bits, δηλαδή να ισχύει Ο(${(\log n)}^c$), για κάποια σταθερά $c$. Προφανώς, η πολυπλοκότητα του ανωτέρω αιτιοκρατικού αλγορίθμου είναι Ο($\sqrt{n}$)=Ο($2^{\frac{1}{2}\log n}$) και, επομένως, ο αλγόριθμος δεν είναι αποτελεσματικός χρονο-πολυωνυμικά.  

Στη συνέχεια, θα εξετάσουμε τυχαίους αλγορίθμους που ανήκουν στην κατηγορία Monte Carlo και θα καταλήξουμε σε έναν πολύ αποτελεσματικό τυχαίο αλγόριθμο. Για παράδειγμα, έστω ότι δίνεται ο αριθμός $n=2773=47\times 59$, που προφανώς δεν είναι πρώτος. Θα μπορούσαμε να ακολουθήσουμε τη λογική του προβλήματος των επαναλαμβανόμενων στοιχείων και να δοκιμάσουμε αν το 2773 διαιρείται με κάποιον ακέραιο που επιλέγεται τυχαία στο διάστημα $[2,\lfloor \sqrt{2773}\rfloor ]=[2,52]$. Επομένως, με πιθανότητα περίπου 2% θα επιλέγαμε το 47 και θα καταλήγαμε ότι το 2773 δεν είναι πρώτος αριθμός, όμως με περίπου 98% θα καταλήγαμε σε λάθος συμπέρασμα. Βέβαια κατά τον έλεγχο αριθμών με πολλά ψηφία (πράγμα που κατ’εξοχήν συμβαίνει στην κρυπτογραφία) η πιθανότητα για ορθή απάντηση θα είναι ακόμη μικρότερη. Θα μπορούσαμε να εκτελέσουμε το πείραμα αυτό περισσότερες φορές, ώστε να αυξήσουμε την πιθανότητα αποκλεισμού του λάθους, όπως φαίνεται στην επόμενη διαδικασία prime2. Η διαδικασία αυτή εκτελεί ένα μεγάλο αριθμό πειραμάτων (large), ώστε η πιθανότητα της ορθής απάντησης να είναι της τάξης $1-n^{-a}$, όπως πρέπει να συμβαίνει στους αλγορίθμους που στηρίζονται σε μία λογική Monte Carlo.

     procedure prime2(n)
1.   for k <-- 1 to large do
2.      i <-- random(1,sqrt(n));
3.      if (n mod i = 0) then return false;
3.   return true

Στο αλγόριθμο αυτό οι αρνητικές απαντήσεις (δηλαδή ότι ο αριθμός δεν είναι πρώτος) είναι με βεβαιότητα ορθές, ενώ οι θετικές απαντήσεις (δηλαδή ότι ο αριθμός είναι πρώτος) είναι ορθές αλλά με μικρή πιθανότητα. Επίσης, η πιθανότητα του λάθους δεν είναι τόσο συνάρτηση του ελεγχόμενου αριθμού αλλά του αποτελέσματος της γεννήτριας τυχαίων αριθμών. Στη συνέχεια, θα εξετάσουμε έναν εναλλακτικό τυχαίο αλγόριθμο που στηρίζεται στο επόμενο θεώρημα του Fermat, του οποίου την απόδειξη μπορούμε να βρούμε σε βιβλία Θεωρίας Αριθμών.  

Θεώρημα.
Αν ο αριθμός $n$ είναι πρώτος, τότε για ισχύει: $a^{n-1}\mathrm{mod}n=1$. 

Απόδειξη.
Μία πρώτη απόδειξη είναι επαγωγική ως προς $a$ και θα αποδείξει την ισοδύναμη πρόταση: $a^n\mathrm{mod}n=a$. Είναι προφανές ότι πάντοτε ισχύει η βασική συνθήκη για $a=1$ (ακόμη και αν ο $n$ δεν είναι πρώτος). Δεχόμαστε ότι ισχύει $a^n\mathrm{mod}n=a$. Θα αποδείξουμε ότι ${(a+1)}^n\mathrm{mod}n=a+1$. Έχουμε ότι:

$${(a+1)}^n=\sum _{i=0}^n\left(\begin{array}{c}n\\ i\end{array}\right)a^{n-i}$$

(13.13)

Ο συντελεστής $\left(\begin{array}{c}n\\ i\end{array}\right)$ είναι διαιρετός δια $n$ εκτός από τις περιπτώσεις $i=0$ και $i=n$. Επομένως, ισχύει:

$${(a+1)}^n\mathrm{mod}n=(a^n+1)\mathrm{mod}n=(a+1)\mathrm{mod}n$$

(13.14)

Μία δεύτερη απόδειξη στηρίζεται στην εξής ιδέα. Έστω οι αριθμοί $1,2,\mathrm{\dots }$, $n-1$, που τους πολλαπλασιάσουμε επί $a$, οπότε προκύπτουν οι αριθμοί $a,2a,\mathrm{\dots }$, $(n-1)a$. Οι αριθμοί αυτοί είναι διακριτοί ως προς mod $n$ και υπάρχουν $n-1$ τέτοιοι αριθμοί. Άρα, οι αριθμοί αυτοί είναι ίδιοι με τους προηγούμενους αλλά με μία άλλη σειρά. Άρα, ισχύει:

	$1\times 2\times \mathrm{\dots }\times (n-1)\mathit{\hspace{1em}}\mathrm{mod}n$	$=$	$a\times 2a\times \mathrm{\dots }\times (n-1)a\mathit{\hspace{1em}}\mathrm{mod}n$
		$=$	$a^{n-1}\times 1\times 2\times \mathrm{\dots }\times (n-1)\mathrm{mod}n$

Συνεπώς, ισχύει η πρόταση. $\mathrm{\square }$  

Ας δοκιμάσουμε το θεώρημα για τον πρώτο αριθμό $n=5$. Πράγματι ισχύει: $4^4\mathrm{mod}\mathrm{\hspace{0.25em}5}=1$, $3^4\mathrm{mod}\mathrm{\hspace{0.25em}5}=1$ και $2^4\mathrm{mod}\mathrm{\hspace{0.25em}5}=1$. Ενώ για αντιπαράδειγμα, ο $n=4$ δεν είναι πρώτος αριθμός και ισχύει: $3^3\mathrm{mod}\mathrm{\hspace{0.25em}4}=3$ και $2^3\mathrm{mod}\mathrm{\hspace{0.25em}4}=0$. Ωστόσο, το θεώρημα περιγράφει μία ικανή συνθήκη αλλά όχι και αναγκαία, δηλαδή δεν ισχύει και κατά την αντίστροφη σειρά. Έτσι, υπάρχουν μη πρώτοι αριθμοί για τους οποίους ισχύει η συνθήκη μερικές φορές. Για παράδειγμα, για το μη πρώτο αριθμό $n=9$ ισχύει: $a^8\mathrm{mod}\mathrm{\hspace{0.25em}9}\ne 1$ για , αλλά $8^8\mathrm{mod}\mathrm{\hspace{0.25em}9}=1$. Έτσι, το 9 λέγεται 8-ψευδοπρώτος (8-pseudoprime). Οι $k$-ψευδοπρώτοι αριθμοί είναι πιο σπάνιοι αριθμοί από τους πρώτους. Για παράδειγμα, το 9 είναι ο μικρότερος ψευδοπρώτος ακέραιος, ενώ ο μικρότερος 2-ψευδοπρώτος είναι ο 341 (δηλαδή ισχύει: $2^{340}\mathrm{mod}\mathrm{\hspace{0.25em}341}=1$).

Με βάση το θεώρημα μπορούμε να σχεδιάσουμε έναν τυχαίο αλγόριθμο, όπου για δεδομένο περιττό αριθμό $n$, με τυχαίο τρόπο θα επιλέγουμε τιμές για το , ώστε να δοκιμάζουμε αρκετές φορές τη συνθήκη του θεωρήματος (και να μην πέσουμε εύκολα στην παγίδα των ψευδοπρώτων). Η επόμενη διαδικασία prime3 αποτυπώνει αυτή την περιγραφή. Παρατηρούμε ότι στην περίπτωση αυτή ο αλγόριθμος θα έχει την αντίστροφη λογική από τη λογική του αλγορίθμου prime2. Έτσι, οι αρνητικές απαντήσεις (δηλαδή ότι ο αριθμός δεν είναι πρώτος) είναι με βεβαιότητα ορθές, ενώ οι θετικές απαντήσεις (δηλαδή ότι ο αριθμός είναι πρώτος) είναι ορθές με μεγάλη πιθανότητα. Σημειώνεται, επίσης, ότι ο διπλός βρόχος while είναι μία ακόμη εκδοχή ύψωσης σε δύναμη (δες Κεφάλαιο 4.4).

     procedure prime3(n)
1.   q <-- n-1;
2.   for i <-- 1 to large do
3.      m <-- q; y <-- 1;
4.      a <-- random(2,n-1); z <-- a;
5.      while (m>0) do
6.         while (m mod 2 = 0) do
7.            z <-- (z*z) mod n; m <-- int(m/2);
8.         m <-- m-1; y <-- (y*z) mod n;
9.      if (y<>1) then rerurn false;
110.  return true

Η διαδικασία prime3 είναι σημαντικά αποτελεσματικότερη σε σχέση με την prime2 αλλά και πάλι δεν έχουμε λύσει το πρόβλημα καθ’ολοκληρία γιατί όπως δείξαμε στο προηγούμενο παράδειγμα το θεώρημα ισχύει κατά τη μία μόνο κατεύθυνση. Ωστόσο, όπως αναφέρεται στη βιβλιογραφία χειρότερη είναι η σύμπτωση των λεγόμενων αριθμών Carmichael, οι οποίοι δεν είναι πρώτοι αλλά πάντοτε ικανοποιούν το θεώρημα του Fermat. Αν και οι αριθμοί αυτοί είναι σπάνιοι, εντούτοις το σύνολό τους είναι άπειρο. Για παράδειγμα, αναφέρεται ότι υπάρχουν 255 τέτοιοι αριθμοί μέχρι το 100.000.000, ενώ οι εννέα μικρότεροι αριθμοί Carmichael είναι οι 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585 και 15841, που περνούν όλες τις συνθήκες για κάθε θετικό $a$ μικρότερο του αντίστοιχου αριθμού.  

Πρόταση.
Ο αριθμός $n$ είναι Carmichael, αν και μόνο αν ισχύει $n=p_1\times p_2\times \mathrm{\dots }\times p_k$, όπου οι $p_1,p_2,\mathrm{\dots },p_k$ είναι πρώτοι αριθμοί και ισχύει: $(n-1)\mathrm{mod}(p_i-1)=0$ για κάθε $i$. $\mathrm{\square }$  

Για παράδειγμα, ισχύει: $561=3\times 11\times 17$, ενώ $560\mathrm{mod}\mathrm{\hspace{0.25em}2}=0,\mathrm{\hspace{0.25em}560}\mathrm{mod}\mathrm{\hspace{0.25em}10}=0$, και $560\mathrm{mod}\mathrm{\hspace{0.25em}16}=0$. Εν πάσει περιπτώσει, η προσέγγιση της διαδικασίας prime3 απειλείται καθώς ο αλγόριθμος αυτός θα δίνει (σπανίως βέβαια) λάθος συμπέρασμα, που θα ισχύει για τις ίδιες πάντοτε περιπτώσεις (δηλαδή ανεξαρτήτως του αποτελέσματος της γεννήτριας τυχαίων αριθμών). Όμως, λύση υπάρχει και στηρίζεται στην εξής πρόταση.  

Πρόταση.
Αν ο $n$ είναι πρώτος αριθμός και ισχύει , τότε η εξίσωση $x^2\mathrm{mod}n=1$ έχει μόνο 2 λύσεις, τις $x=1$ και $x=n-1$.  

Απόδειξη.
Η εξίσωση αυτή σημαίνει ότι $(x^2-1)\mathrm{mod}n=0\Rightarrow (x+1)(x-1)\mathrm{mod}n=0$. Εφόσον το $n$ είναι πρώτος αριθμός και $1\le x\le n$, έπεται ότι το $n$ πρέπει να διαιρεί είτε το $x-1$ είτε το $x+1$. $\mathrm{\square }$  

Από την πρόταση αυτή συνάγεται ότι αν υπάρχουν και άλλες ρίζες πλην των $x=1$ και $x=n-1$, τότε ο αριθμός $n$ δεν είναι πρώτος. Πράγματι, σε σχέση με το 561, το μικρότερο αριθμό Carmichael, ισχύει ότι η εξίσωση: $x^2\mathrm{mod}\mathrm{\hspace{0.25em}561}=1$ έχει τις δύο προφανείς λύσεις $x=1$ και $x=560$ καθώς και μερικές ακόμα, όπως $x=494$, $x=373$ κοκ. Άρα, ο $561$ δεν είναι πρώτος. Στην πρόταση αυτή, λοιπόν, στηρίζεται η επόμενη διαδικασία prime4 που βελτιώνει τη διαδικασία prime3. Μάλιστα, η εντολή PrimeQ του Mathematica υλοποιεί αυτόν τον αλγόριθμο, που φέρει το όνομα των Miller-Rabin.

     procedure prime2(n,alpha)
1.   q <-- n-1;
2.   for i <-- 1 to alpha*log(n) do
3.      m <-- q; y <-- 1;
4.      a <-- random(2,n-1); z <-- a;
5.      while (m>0) do
6.         while (m mod 2 = 0) do
7.            x <-- z; z <-- (z*z) mod n;
8.            if ((z=1) and (x<>1) and (x<>q)) then
9 .              return false;
10.           m <-- int(m/2);
11.        m <-- m-1; y <-- (y*z) mod n;
12.     if (y<>1) then rerurn false;
13.  return true

Σύμφωνα, λοιπόν, με τη διαδικασία αυτή, αν το $n$ είναι πρώτος, τότε και θα ικανοποιείται το θεώρημα του Fermat αλλά και δεν θα υπάρχει κάποια μη τετριμμένη λύση σύμφωνα με το προηγούμενο θεώρημα. Έτσι, ο αλγόριθμος αυτός δίνει πάντοτε ορθή απάντηση για τους πρώτους αριθμούς και τους αριθμούς Carmichael. Ωστόσο, μπορεί να δώσει λάθος αποτέλεσμα αν πέσει στην παγίδα των ψευδοπρώτων αριθμών (δηλαδή ο αριθμός να μην είναι πρώτος, αλλά στην έξοδο να δοθεί σαν πρώτος). Η αξιοπιστία του αλγορίθμου στην περίπτωση αυτή εξαρτάται από τη γεννήτρια των τυχαίων αριθμών και τις τιμές της παραμέτρου a (εντολή 4), οι οποίες θα επιλεγούν για τη δοκιμή. Ας ονομάσουμε μάρτυρα (witness) την τιμή του $a$, η οποία αποκαλύπτει τη συνθετότητα του $n$. Η πιθανότητα επιλογής μίας τιμής μάρτυρα για το $a$ δίνεται (χωρίς απόδειξη) από την επόμενη πρόταση, η οποία αποτελεί τη βάση για να φθάσουμε στην πολυπλοκότητα της prime4.  

Απόδειξη.  Με βάση το Λήμμα 13.8 η εκτέλεση κάθε επανάληψης του αλγορίθμου δίνει μάρτυρα $a$ για την συνθετότητα του ακεραίου $n$ με πιθανότητα $\ge 1/2$. Ο αλγόριθμος δεν θα ανακαλύψει ότι ο $n$ είναι σύνθετος αν είναι τόσο άτυχος, ώστε σε κάθε επανάληψη από τις συνολικά $k$ επαναλήψεις να μην βρίσκει μάρτυρα. Η πιθανότητα αυτή είναι τουλάχιστον $2^{-k}$.  

Απόδειξη.  Αν το $n$ είναι πρώτος, τότε πάντοτε λαμβάνουμε ορθή απάντηση, οπότε αυτή η περίπτωση δεν μας απασχολεί. Ας υποθέσουμε ότι το $n$ δεν είναι πρώτος. Από το Λήμμα 13.9 προκύπτει ότι η πιθανότητα κανείς από τους επιλεγόμενους $a\times \log n$ τυχαίους αριθμούς να μην είναι μάρτυρας είναι $\le {(\frac{1}{2})}^{a\log n}=n^{-a}$. Δηλαδή, η διαδικασία prime4 θα δώσει λανθασμένη απάντηση με πιθανότητα $\le n^{-a}$, οπότε έτσι ικανοποιείται η απαίτηση των αλγορίθμων Monte Carlo για επιτυχία με μεγάλη πιθανότητα ίση με $1-n^{-a}$. Καθώς κάθε βρόχος while συνεπάγεται Ο($\log n$) επαναλήψεις, έπεται ότι η πολυπλοκότητα του αλγορίθμου είναι Ο(${\log }^{2}n$).  

Μερικά επιλογικά σχόλια αναφορικά με το πρόβλημα του ελέγχου πρώτων αριθμών, για το οποίο μόλις μελετήσαμε μία αποτελεσματική λύση. Μέχρι πρόσφατα θεωρούνταν ότι το πρόβλημα αυτό δεν υπήρχε πολυωνυμικός αιτιοκρατικός αλγόριθμος. Στις 6 Αυγούστου του 2002, τρεις ερευνητές του Institute of Technology in Kampur, οι M. Agrawal, N. Kayal και N Saxena, δημοσίευσαν στο διαδίκτυο μία μελέτη που λύνει το πρόβλημα σε πολυωνυμικό χρόνο. Έτσι, ανοίγει μία νέα περίοδος στην έρευνα των γρήγορων μαθηματικών αλγορίθμων της Θεωρίας Αριθμών.

Στο Κεφάλαιο 8.4 είχαμε εξετάσει το πρόβλημα των στατιστικών διάταξης σε συνδυασμό με τη γρήγορη ταξινόμηση. Με παρόμοιο τρόπο, μπορούμε να διατυπώσουμε μία τυχαιοποιημένη εκδοχή της συνάρτησης για την επιλογή του $k$-οστού στοιχείου ενός αταξινόμητου πίνακα υιοθετώντας κάθε φορά μία τυχαία επιλογή του άξονα. Με παρόμοιο, επίσης, τρόπο θα μπορούσαμε να διατυπώσουμε την αντίστοιχη ανάλυση, που θα κατέληγε στο ίδιο συμπέρασμα, δηλαδή πολυπλοκότητα Ο($n$). Η προσέγγιση αυτή είναι σχετικά εύκολη υπόθεση για τον αναγνώστη και για το λόγο αυτό στην παρούσα παράγραφο θα ασχοληθούμε με ένα νέο πρόβλημα: την εύρεση του προσεγγιστικού μεσαίου (approximate median). Τυπικά το πρόβλημα ορίζεται ως εξής:  

Ορισμός.
Δεδομένου ενός πίνακα $A$ με $n$ αριθμούς, τότε $ϵ$-μεσαίος λέγεται ένας αριθμός $q$, τέτοιος ώστε και $|A[i]>q|\le (1-ϵ)n$. $\mathrm{\square }$  

Για την ευκολία της επίλυσης του προβλήματος θεωρούμε ότι οι $n$ τιμές του πίνακα είναι οι αριθμοί $0,\frac{1}{n},\frac{2}{n},\mathrm{\dots },\frac{n-1}{n}$, ενώ επίσης δεχόμαστε ότι το $n$ είναι δύναμη του 3, δηλαδή ισχύει $n=3^k$. Θεωρούμε τη δομή ενός πλήρους τριαδικού δένδρου με $L=n$ φύλλα. Λαμβάνουμε μία τυχαία διάταξη από τις $n!$ συνολικά και θεωρούμε ότι τα στοιχεία αυτής της διάταξης αποτελούν τα φύλλα του δένδρου. Συνεχίζουμε την κατασκευή του δένδρου από το επίπεδο των φύλλων προς το επίπεδο της ρίζας αντιστοιχώντας 3 φύλλα σε ένα κόμβο-πατέρα με περιεχόμενο ίσο προς το μεσαίο των 3 στοιχείων των κόμβων-παιδιών. Η διαδικασία συνεχίζεται αναδρομικά μέχρι το επίπεδο της ρίζας. Στο σημείο αυτό, μία πρώτη παρατήρηση είναι ότι η τάξη του στοιχείου της ρίζας θα είναι $n/2$ στη μέση περίπτωση. Το Σχήμα 13.6 απεικονίζει ένα παράδειγμα με $n=9$.

Έστω ότι με συμβολίζουμε την πιθανότητα η έξοδος του αλγορίθμου να μην είναι μεγαλύτερη από $x$, δεδομένου ενός δένδρου με ύψος $h$. Για το επίπεδο των φύλλων ισχύει η βασική συνθήκη . Θα υπολογίσουμε την πιθανότητα με αναδρομικό τρόπο.

Έστω η ρίζα του δένδρου, η οποία έχει 3 παιδία με τιμές $c_1,c_2,c_3$. Η μεσαία τιμή των τριών αυτών τιμών μπορεί να είναι λιγότερο από $x$, αν και μόνον αν δύο από τις τιμές αυτές είναι μικρότερη από $x$. Αυτό μπορεί να συμβεί σε δύο περιπτώσεις:

• •

  ακριβώς δύο από τις τιμές των παιδιών είναι λιγότερο από $x$.

• •

  και οι τρεις τιμές είναι λιγότερο από $x$.

Έτσι, προκύπτουν οι σχέσεις:

		$=$
		$=$

Με διαδοχικές αντικαταστάσεις έχουμε:

		$\le$
		$\le$	${\mathrm{3\hspace{0.25em}3}}^2{\mathrm{\hspace{0.25em}3}}^4\mathrm{\dots }{3}^{2^{h-1}}{x}^{2^h}={\mathrm{\hspace{0.25em}3}}^{1+2+4+\mathrm{\dots }+2^{h-1}}{x}^{2^h}$
		$=$	$3^{2^h-1}{x}^{2^h}={\displaystyle \frac{1}{3}}{\mathrm{\hspace{0.25em}3}}^{2^h}{x}^{2^h}={\displaystyle \frac{1}{3}}{(3x)}^{2^h}$

Έτσι, φθάνουμε στο συμπέρασμα ότι με ένα τυχαίο αλγόριθμο μπορούμε να βρούμε τον προσεγγιστικό μεσαίο με πολύ μεγάλη πιθανότητα.

Ο αλγόριθμος ελέγχου για το αν ένας αριθμός είναι πρώτος σχεδιάσθηκε από τον Rabin [150], ενώ όπως αναφέρθηκε και στο κυρίως κείμενο σε μία πρόσφατη δημοσίευση οι Agrawal, Kayal και Saxena [1] έδωσαν έναν αιτιοκρατικό αλγόριθμο αποδεικνύοντας ότι το συγκεκριμένο πρόβλημα τελικά ανήκει στη κλάση $P$. Και τους δυο αλγορίθμους μπορείτε, επίσης, να τους βρείτε στο βιβλίο [173].

Μία αντιπροσωπευτική περιοχή εφαρμογής τυχαιοποιημένων αλγορίθμων στα οποία δεν αναφερθήκαμε είναι η μέθοδος της διασποράς (hashing). Αυτή η ιδέα της χρήσης της μεθόδου της διασποράς, ώστε να ξεπεράσουμε το λογαριθμικό όριο για την πράξη της αναζήτησης σε μία RAM τέθηκε για πρώτη φορά από τον Yao [201]. Από τότε έχει γίνει πολλή δουλειά όσον αφορά τον ορισμό συναρτήσεων διασποράς που περιλαμβάνει μεταξύ άλλων τις τέλειες συναρτήσεις διασποράς [180] και τις καθολικές συναρτήσεις διασποράς [190]. Μία πρόσφατη και απλή μέθοδος διασποράς είναι και η διασπορά του κούκου (cuckoo-hashing) [139].

Για αυτόν που ενδιαφέρεται για μία βαθύτερη μελέτη των τυχαιοποιημένων αλγορίθμων και των χαρακτηριστικών τους, τα βιβλία [131] και [129] αποτελούν εξαιρετική εισαγωγή.

1. 1.

   Τα φίλτρα Bloom μπορούν να χρησιμοποιηθούν, για να υπολογίσουμε προσεγγιστικά τη διαφορά συνόλων. Έστω δύο σύνολα $\mathrm{{\rm X}}$ και $\mathrm{{\rm Y}}$ καθένα από τα οποία έχει $n$ στοιχεία. Δημιουργούμε Bloom φίλτρα και για τα δύο σύνολα χρησιμοποιώντας τον ίδιο αριθμό από bits $m$ και πλήθος συναρτήσεων κατακερματισμού $k$. Να καθορίσετε το αναμενόμενο πλήθος bits όπου τα δύο φίλτρα διαφέρουν μεταξύ τους σαν συνάρτηση των $m,n,k$ και $|X\cap Y|$.

2. 2.

   Να εισάγετε την παρακάτω ακολουθία αριθμών με την σειρά που εμφανίζεται σε (α) μία λίστα παράλειψης ($p=1/3$), (β) σε ένα δέντρο αναζήτησης σωρού και (γ) σε ένα φίλτρο Bloom ($m=30,k=2$ - επιλέξτε εσείς τις συναρτήσεις κατακερματισμού).

   $63,30,36,31,12,50,35,5,27,59,43,17$

   Έπειτα, διαγράψτε τα στοιχεία $59,5$ από τη λίστα παράλειψης και από το δέντρο αναζήτησης σωρού.

3. 3.

   Τα φίλτρα Bloom δεν έχουν την δυνατότητα διαγραφής ενός στοιχείου. Μπορείτε να αλλάξετε τα φίλτρα Bloom, ώστε να είναι σε θέση να υποστηρίζουν την πράξη της διαγραφής; Πόσος είναι ο χώρος που θα χρησιμοποιούν σε αυτή την περίπτωση;

4. 4.

   Έστω $ϵ,\delta$ πραγματικοί αριθμοί, έτσι ώστε: . Έστω $\mathrm{{\rm A}}$ ένας τυχαίος αλγόριθμος που υπολογίζει μία συνάρτηση $F$ όπου:

   $P(A(x)=F(x))\ge ϵ$ και $P(A(x)=\mathrm{?})=1-P(A(x)=F(x))$

   Έστω ότι για κάθε $k\in N,k\ge 2$, $A_k$ είναι ο τυχαίος αλγόριθμος, ώστε για κάθε είσοδο $x$ ο $\mathrm{{\rm A}}$ εκτελείται $k$ φορές στο $x$. Η έξοδος του $A_k$ είναι $\mathrm{?}$ αν και μόνο αν και οι $k$ εκτελέσεις του $\mathrm{{\rm A}}$ στο $x$ έδωσαν έξοδο $\mathrm{?}$ (έξοδος $\mathrm{?}$ σημαίνει ότι η έξοδος είναι λανθασμένη). Σε κάθε άλλη περίπτωση ο αλγόριθμος ${\mathrm{{\rm A}}}_k$ υπολογίζει το σωστό αποτέλεσμα $F(x)$. Να υπολογίσετε το μικρότερο $k$, ώστε ώστε $P(A_k(x)=F(x))\ge \delta$.

5. 5.

   Έστω ότι $A$ είναι ένας Monte Carlo αλγόριθμος, έτσι ώστε για κάθε είσοδο $x$, υπολογίζει το σωστό αποτέλεσμα $F(x)$ με πιθανότητα $\frac{1}{2}+{ϵ}_x$, όπου ${ϵ}_x$ εξαρτάται από το μέγεθος του $x$ (αριθμός bits, έστω $|x|$). Έστω $\delta$ μία σταθερά, . Πόσες επαναλήψεις $k=k(|x|)$ του $A$ στο $x$ πρέπει να γίνουν, έτσι ώστε να επιτύχουμε $P(A_k(x)=F(x)))\ge 1-\delta$, αν ${ϵ}_x=\frac{1}{|x|}$.

6. 6.

   Έστω ότι $\mathrm{{\rm A}}$ είναι ένας τυχαίος αλγόριθμος που υπολογίζει μία συνάρτηση $F$ με $P(A(x)=F(x))\ge 1/3$ για κάθε $x$. Επίσης υποθέστε ότι ξέρετε ότι $P(A(x)=\alpha )\le 1/4$ για κάθε λανθασμένο αποτελέσμα $\alpha$ (η πιθανότητα υπολογισμού λανθασμένης τιμής είναι το πολύ 1/4). Μπορείτε να χρησιμοποιήσετε αυτή την πληροφορία, ώστε να σχεδιάσετε έναν χρήσιμο τυχαίο αλγόριθμο για τη συνάρτηση $F$;

7. 7.

   $n$ σφαίρες ρίχνονται σε $n$ κάδους σε μία επαναληπτική διαδικασία. Σε κάθε επανάληψη κάθε σφαίρα επιλέγει να πέσει σε ένα κάδο ισοπίθανα. Αν μία σφαίρα πέσει μόνη της σε έναν κάδο τότε η σφαίρα αυτή αφαιρείται και η διαδικασία επαναλαμβάνεται με τις υπόλοιπες σφαίρες (αυτό το παιχνίδι μοντελοποιεί ένα απλό σύστημα όπου $n$ διεργασίες χρησιμοποιούν τυχαία $n$ συσκευές επικοινωνίας και κάθε συσκευή εξυπηρετεί μόνο, αν της πέσει μία και μόνο μία διεργασία, αλλιώς τις απορρίπτει όλες).

   Αν υπάρχουν $b$ σφαίρες στην αρχή της επανάληψης, ποιό είναι το αναμενόμενο πλήθος σφαιρών στο τέλος μίας επανάληψης;

8. 8.

   Δοθέντος ενός δικαίου νομίσματος (πιθανότητα για Γράμματα (Γ) ή Κορώνα (Κ) είναι $1/2$) να εξομοιώσετε ένα κίβδηλο νόμισμα όπου η πιθανότητα εμφάνισης Κ είναι $p$ και η πιθανότητα εμφάνισης Γ είναι $1-p$. Προσπαθείστε να ελαχιστοποιήσετε το μέσο αριθμό πειραμάτων (στρίψιμο νομίσματος) του δικαίου νομίσματος.

9. 9.

   Θεωρείστε τον παρακάτω αλγόριθμο εύρεσης ελαχίστου στοιχείου σε έναν μη ταξινομημένο πίνακα:

        procedure random(A[1,...,n])
   1.   min=Infinity;
   2.   for i <-- 1 to n in random order do
   3.      if (A[i]<min)
   4.      	min<--A[i];
   5.      return min
   

   (α) Στη χειρότερη περίπτωση, πόσες φορές θα εκτελεστεί η γραμμή 4;

   (β) Ποιά είναι η πιθανότητα η γραμμή 4 να εκτελεστεί κατά την $n$-ιοστή επανάληψη;

   (γ) Ποιος είναι ο ακριβής αναμενόμενος αριθμός εκτελέσεων της γραμμής 4;

10. 10.

    Έστω $S$ ένα σύνολο $n$ σημείων στο επίπεδο. Ένα σημείο $p$ στο $S$ καλείται Pareto-βέλτιστο αν δεν υπάρχει άλλο σημείο που να είναι πιο πάνω και δεξιά από το $p$.

    (α) Σχεδιάστε και περιγράψτε έναν αλγόριθμο που υπολογίζει τα Pareto-βέλτιστα σημεία του $S$ σε χρόνο $O(n\log n)$.

    (β) Έστω ότι κάθε σημείο του $S$ επιλέγεται ανεξάρτητα και ισοπίθανα από το μοναδιαίο τετράγωνο $[0,1]\times [0,1]$. Ποιο είναι το αναμενόμενο πλήθος Pareto-βέλτιστων σημείων στο $S$;

11. 11.

    Έστω ότι παρακολουθούμε μία ροή (stream) από δεδομένα τα οποία τα επεξεργαζομαστε ένα κάθε φορά. Από τη στιγμή που ένα στοιχείο $x$ της ροής επεξεργαστεί και έρθει το επόμενο του, το $x$ χάνεται. Θέλουμε να πάρουμε ένα τυχαίο δείγμα $k$ διαφορετικών στοιχείων από τη ροή με τους παρακάτω περιορισμούς:

    • –

      Μπορούμε να αποθηκεύσουμε μόνο $k$ στοιχεία κάθε χρονική στιγμή (το μέγεθος της μνήμης χωράει $k$ στοιχεία).

    • –

      Δεν γνωρίζουμε το συνολικό αριθμό πακέτων στη ροή.

    • –

      Αν αποφασίσουμε να μην αποθηκεύσουμε ένα στοιχείο την στιγμή που φτάνει σε εμάς, τότε αυτό χάνεται για πάντα.

    Σχεδιάστε έναν αλγόριθμο ώστε όταν η ροή τερματιστεί, θα έχουμε αποθηκεύσει ένα υποσύνολο της ροής με $k$ στοιχεία επιλεγμένα με ίση πιθανότητα από όλα τα στοιχεία της ροής. Αν ο συνολικός αριθμός στοιχείων της ροής είναι μικρότερος του $k$, τότε θα πρέπει να αποθηκεύσετε όλα τα πακέτα.

12. 12.

    Μας δίνεται ένα κίβδηλο νόμισμα με πιθανότητα εμφάνισης Κορώνας (Κ) $p$ και Γραμμάτων (Γ) $1-p$. Πως θα εξομοιώσετε ένα δίκαιο νόμισμα (πιθανότητα Κ και Γ είναι $1/2$) χρησιμοποιώντας το κίβδηλο νόμισμα;

13. 13.

    Έστω ότι ο $\mathrm{{\rm X}}[1\mathrm{\dots }n]$ είναι ένας πίνακας πραγματικών αριθμών (διαφορετικών μεταξύ τους), και έστω $N[1\mathrm{\dots }n]$ ένας πίνακας δεικτών για τον πίνακα $\mathrm{{\rm X}}$ με την εξής ιδιότητα: Αν το $X[i]$ είναι το μεγαλύτερο στοιχείο του $X$, τότε το $X[N[i]]$ είναι το μικρότερο στοιχείο του $X$. Διαφορετικά το $X[N[i]]$ είναι το μικρότερο στοιχείο του $X$ μεγαλύτερο από το $X[i]$. Για παράδειγμα:

    $i$	1	2	3	4	5	6	7	8	9
    $X[i]$	83	54	16	31	45	99	78	62	27
    $N[i]$	6	8	9	5	2	3	1	7	4

    Περιγράψτε και αναλύστε έναν τυχαίο αλγόριθμο που αποφασίζει αν ένας αριθμός $x$ εμφανίζεται στον πίνακα $\mathrm{{\rm X}}$ σε αναμενόμενο χρόνο $O(\sqrt{n})$. Ο αλγόριθμος που θα προτείνετε δεν πρέπει να μεταβάλει τους πίνακες $X$ και $N$.

14. 14.

    Ένα δέντρο πλειοψηφίας είναι ένα πλήρες δέντρο βάθους $d$, όπου κάθε φύλλο έχει τιμή $0$ ή $1$. Η τιμή ενός εσωτερικού κόμβου είναι η πλειοψηφούσα τιμή των παιδιών του. Θα ασχοληθούμε με το πρόβλημα εύρεσης της τιμής της ρίζας ενός τριαδικού πλειοψηφικού δέντρου δοθείσης της ακολουθίας των $3^d$ φύλλων σαν είσοδο. Για παράδειγμα, αν $d=2$ και τα φύλλα έχουν τιμή $1,0,0,0,1,0,1,1,1$ η ρίζα έχει τιμή $0$ (Σχήμα 13.7).

    

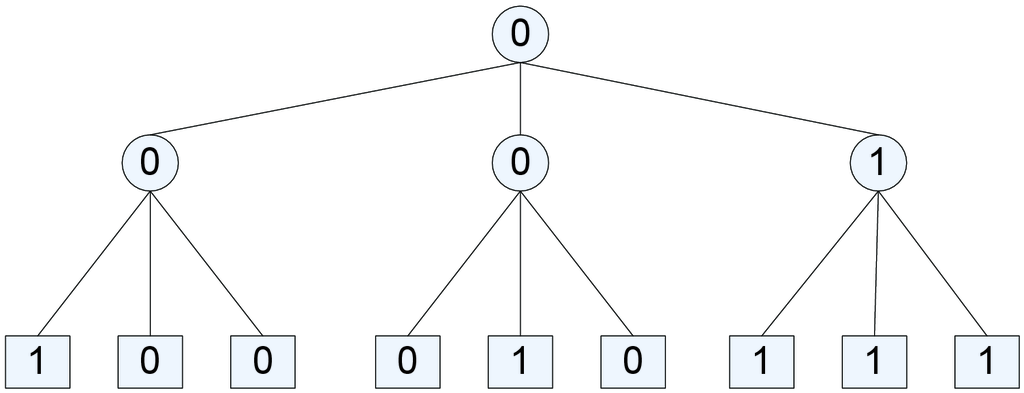
    Περιγράψτε και αναλύστε έναν τυχαίο αλγόριθμο που βρίσκει την τιμή της ρίζας σε αναμενόμενο χρόνο $O(c^d)$ για κάποια σταθερά .

    [Υπόδειξη: Κοιτάξτε την απλή περίπτωση $d=1$. Έπειτα, εφαρμόστε αναδρομικά την διαδικασία αυτή.]

15. 15.

    Έστω ότι θέλουμε να φτιάξουμε ένα αλγόριθμο $RP(n)$ που βρίσκει μία αναδιάταξη των ακεραίων από $\{1,\mathrm{\dots },n\}$, όπου κάθε δυνατή αναδιάταξη έχει ίδια πιθανότητα εμφάνισης. Ο παρακάτω αλγόριθμος είναι μία τέτοια υλοποίηση:

         procedure RP(n)
    1.   for i <-- 1 to n
    2.      π[i]<--NULL; //Το π είναι ο πίνακας που θα περιέχει
                         //την αναδιάταξη
    3.   for i <-- 1 to n
    4.      j<--Random(n); //Επιστρέφει ένα τυχαίο ακέραιο στο
                           //διάστημα [1,n] ισοπίθανα
    5.      while(π[j]!=NULL)
    6.         j<--Random(n);
    7.      π[j]=i;
    8.   return(π);
    

    Απόδείξτε ότι ο αλγόριθμος είναι σωστός (να δείξετε δηλαδή ότι πράγματι παράγει μία αναδιάταξη ισοπίθανα). Ποιός είναι ο αναμενόμενος χρόνος εκτέλεσης του συγκεκριμένου αλγόριθμου;