Σχεδίαση και Ανάλυση Αλγορίθμων 10 Βασικά Στοιχεία Πολυπλοκότητας 12 Αλγόριθμοι Συμβολοσειρών

Κεφάλαιο 11Αλγόριθμοι Γραφημάτων

Ο γράφος ή γράφημα (graph) είναι η γενικότερη μορφή δομής δεδομένων, καθώς όλες οι δομές μπορούν να θεωρηθούν ως υποπεριπτώσεις των γράφων. Η Θεωρία Γράφων (Graph Theory) είναι ένα τεράστιο αντικείμενο μελέτης και έρευνας και διδάσκεται ως ανεξάρτητο μάθημα σε όλα τα τμήματα Πληροφορικής αλλά και άλλων επιστημών (πχ. Μαθηματικών, Φυσικής, Ηλεκτρολόγων Μηχανικών κλπ.). Στην Πληροφορική οι γράφοι χρησιμοποιούνται στη μελέτη των Βάσεων Δεδομένων, Γλωσσών Προγραμματισμού, Δικτύων Υπολογιστών, Λειτουργικών Συστημάτων, του Παγκόσμιου Ιστού κλπ. Εκτός από τις προηγούμενες επιστήμες οι γράφοι χρησιμοποιούνται για την επίλυση πολλών πρακτικών προβλημάτων ποικίλων επιστημονικών περιοχών, όπως στην Ανθρωπολογία, Γενετική μηχανική, Γεωγραφία, Γλωσσολογία, Κοινωνιολογία, Κυβερνητική, Οικονομικά, Στατιστική, Χημεία κλπ.

Οπωσδήποτε, το κεφάλαιο αυτό δεν έχει στόχο την κάλυψη της Θεωρίας Γράφων. Αρχικός σκοπός είναι η παρουσίαση της απαραίτητης ονοματολογίας, καθώς επίσης και η εξέταση των τεχνικών αναπαράστασης της δομής του γράφου, οι οποίες παίζουν καθοριστικό ρόλο στην εύρεση των πολυπλοκοτήτων των διαφόρων αλγορίθμων. Σε αλγοριθμικό επίπεδο θα εξετασθούν εισαγωγικοί αλγόριθμοι, ενώ σε επόμενα κεφάλαια θα μελετηθούν επιπλέον αλγόριθμοι γράφων με συνθετότερα αναλυτικά εργαλεία.

11.1 Βασικές Έννοιες

Ένας γράφος $G$ αποτελείται από δύο σύνολα $V$ και $E$ . Το σύνολο $V$ είναι ένα μη κενό σύνολο με στοιχεία τις κορυφές (vertices) ή κόμβους (nodes) του γράφου. Το σύνολο $Ε$ έχει στοιχεία τα ζεύγη κορυφών του γράφου, τα οποία ορίζουν τις ακμές (edges) του γράφου. Τα σύμβολα $V(G)$ , $E(G)$ και $G(V,E)$ χρησιμοποιούνται για την αναπαράσταση των συνόλων $V$ , $E$ και του γράφου $G$ αντιστοίχως. Οι κορυφές ή οι ακμές ενός γράφου χαρακτηρίζονται από ένα μοναδικό όνομα που ονομάζεται επιγραφή ή ετικέτα (label).

Ζυγισμένος (weighted) λέγεται ο γράφος με ακμές που χαρακτηρίζονται από έναν αριθμό που ονομάζεται βάρος (weight) της ακμής. Πρακτικά, το βάρος μπορεί να δηλώνει έννοιες, όπως το κόστος μετάβασης από τη μία κορυφή στην άλλη, τον απαιτούμενο χρόνο για να διασχισθεί η ακμή κλπ.

Ένας γράφος ονομάζεται μη κατευθυνόμενος (undirected), αν τα ζεύγη των κορυφών που ορίζουν τις ακμές του στερούνται διάταξης. Στους κατευθυνόμενους (directed) γράφους κάθε ακμή συμβολίζεται με το κατευθυνόμενο ζεύγος $<v_{1},v_{2}>$ , όπου $v_{1}$ είναι η ουρά (head) και $v_{2}$ η κεφαλή (head) της ακμής. Συνεπώς, οι ακμές ( $v_{1},v_{2}$ ) και ( $v_{2},v_{1}$ ) ταυτίζονται, ενώ οι ακμές $<v_{1},v_{2}>$ και $<v_{2},v_{1}>$ είναι διαφορετικές. Ένας μη κατευθυνόμενος γράφος μπορεί να θεωρηθεί ως ένας συμμετρικός (symmetric) κατευθυνόμενος γράφος.

Στο Σχήμα 11.1 παρουσιάζονται οι γράφοι $G_{1}$ , $G_{2}$ και $G_{3}$ , από τους οποίους οι $G_{1}$ και $G_{2}$ είναι μη κατευθυνόμενοι, ενώ ο $G_{3}$ είναι κατευθυνόμενος και οι ακμές του παριστάνονται με βέλη που κατευθύνονται από την ουρά προς την κεφαλή. Ειδικά, ο γράφος $G_{2}$ ανήκει σε κατηγορία γράφων, τα λεγόμενα δένδρα. Με βάση τα ανωτέρω είναι εύκολο να αποδειχθεί η εξής πρόταση.

Πρόταση.
Ο μέγιστος αριθμός ακμών για κάθε μη κατευθυνόμενο γράφο με $n$ κορυφές είναι $Ε_{max}=n(n-1)/2$ . Αν ο γράφος είναι κατευθυνόμενος, τότε ισχύει $E_{max}=n(n-1)$ . $\Box$

Ένας (μη) κατευθυνόμενος γράφος με $n$ κορυφές λέγεται πλήρης (complete), αν έχει ακριβώς $n(n-1)$ (αντιστοίχως, $n(n-1)/2$ ) ακμές. Για παράδειγμα, ο γράφος $G_{1}$ του Σχήματος 11.1 είναι πλήρης. Αν ο αριθμός των ακμών ενός γράφου είναι μεγάλος σε σχέση με το $E_{max}$ , τότε ο γράφος λέγεται πυκνός (dense), αλλιώς λέγεται αραιός (sparse).

Αν ( $v_{1},v_{2}$ ) είναι μία ακμή του συνόλου $E(G)$ , τότε οι κορυφές $v_{1}$ και $v_{2}$ λέγονται διπλανές (adjacent) ή γειτονικές (neighboring) και η ακμή ( $v_{1},v_{2}$ ) ονομάζεται προσκείμενη (incident) στις κορυφές $v_{1}$ και $v_{2}$ . Αν δύο κορυφές $v_{1}$ και $v_{2}$ δεν συνδέονται μεταξύ τους με ακμή, τότε λέγονται ανεξάρτητες (independent). Αν $<v_{1},v_{2}>$ είναι μία κατευθυνόμενη ακμή, τότε η κορυφή $v_{1}$ λέγεται διπλανή προς (adjacent to) τη $v_{2}$ και η κορυφή $v_{2}$ διπλανή από (adjacent from) τη $v_{1}$ .

Σχήμα 11.2: Υπογράφοι των γράφων $G_{1}$ και $G_{2}$ .

Αν για ένα γράφο $G^{\prime}$ ισχύουν οι σχέσεις $V(G^{\prime})\subseteq V(G)$ και $E(G^{\prime})\subseteq E(G)$ , τότε ο γράφος αυτός ονομάζεται υπογράφος (subgraph) του γράφου $G$ . Στο Σχήμα 11.2 φαίνονται δύο υπογράφοι καθενός εκ των γράφων $G_{1}$ και $G_{3}$ του Σχήματος 11.1.

Moνοπάτι (path) από την κορυφή $v_{p}$ στην κορυφή $v_{q}$ του γράφου $G$ ορίζεται η ακολουθία των κορυφών $v_{p},v_{i_{1}},v_{i_{2}},...,v_{i_{n}},v_{q}$ που έχουν την ιδιότητα ότι οι ακμές ( $v_{p},v_{i_{1}}$ ), ( $v_{i_{1}},v_{i_{2}}$ ), …, ( $v_{i_{n}},v_{q}$ ) ανήκουν στο $E(G)$ . Αν ο γράφος $G$ είναι κατευθυνόμενος, τότε η ακολουθία των ακμών του μονοπατιού συμβολίζεται με $<v_{p},v_{i_{1}}>$ , $<v_{i_{1}},v_{i_{2}}>,$ …, $<v_{i_{n}},v_{q}>$ . Μήκος (length) μονοπατιού είναι ο αριθμός των ακμών του μονοπατιού. Απλό μονοπάτι (simple path) λέγεται το μονοπάτι εκείνο όπου όλες οι κορυφές - εκτός ενδεχομένως από την πρώτη και την τελευταία - είναι διαφορετικές. Ένα μονοπάτι ( $v_{i_{1}},v_{i_{2}},\ldots,v_{i_{n}}$ ) συμβολίζεται επίσης και ως ( $i_{1},i_{2},\ldots,i_{n}$ ).

Kύκλος (cycle) είναι ένα κλειστό μονοπάτι, όπου ταυτίζεται η πρώτη και η τελευταία κορυφή. Από τον ορισμό αυτό συμπεραίνεται ότι κάθε δένδρο είναι ένας γράφος χωρίς κύκλους. Ένας κατευθυνόμενος γράφος χωρίς κύκλους ονομάζεται “dag” (directed acyclic graph). Για παράδειγμα, το μονοπάτι 1,2,3,1 είναι ένας κύκλος στο $G_{1}$ και το 1,2,1 είναι κύκλος στο $G_{3}$ . Ένας κύκλος που περνά από όλες τις κορυφές ενός συνδεδεμένου γράφου $G$ λέγεται κύκλος του Hamilton. Αν από ένα κύκλο του Hamilton διαγραφεί μία ακμή, τότε απομένει ένα μονοπάτι του Hamilton. Ένας κύκλος που περνά από όλες τις ακμές ενός γράφου μία φορά και καταλήγει στην αρχική κορυφή λέγεται κύκλος του Euler.

Το δάσος (forest) είναι ένας άκυκλος γράφος, όπου κάθε κορυφή έχει ένα ή κανένα πρόγονο. Το δένδρο μπορεί να θεωρηθεί ως ένα δάσος, όπου μόνο μία κορυφή (δηλαδή η ρίζα) δεν έχει πρόγονο. Κάθε δάσος αποτελείται από δένδρα, ενώ σε ένα διατεταγμένο δάσος (ordered forest) τα δένδρα βρίσκονται σε σχέση διάταξης. Δοθέντος ενός γράφου $G$ , το δάσος $F$ ονομάζεται ζευγνύον (spanning) αν:

•

το $F$ είναι υποσύνολο του $G$ και περιέχει όλους τους κόμβους του $G$ ,
•

το $F$ είναι διατεταγμένο δάσος που περιέχει τα δένδρα $T_{1},T_{2},...,T_{n}$ ,
•

το $T_{i}$ περιέχει όλους του κόμβους του $G$ , οι οποίοι είναι προσπελάσιμοι από τη ρίζα του $T_{i}$ και δεν περιέχονται στο δένδρο $T_{j}$ , όπου $j<i$ .

Το $F$ είναι ένα ζευγνύον δένδρο (spanning tree) του $G$ , αν είναι ένα ζευγνύον δάσος του $G$ και αποτελείται από ένα μόνο δένδρο με $n-1$ ακμές.

Σε ένα μη κατευθυνόμενο γράφο $G$ δύο κορυφές $v_{1}$ και $v_{2}$ λέγονται συνδεδεμένες (connected) αν υπάρχει ένα μονοπάτι στο $G$ από την κορυφή $v_{1}$ στην κορυφή $v_{2}$ . Ένας γράφος ονομάζεται συνδεδεμένος αν κάθε ζεύγος κορυφών είναι συνδεδεμένες. Συνεπώς, ένα δένδρο είναι ένας συνδεδεμένος γράφος χωρίς κύκλους.

Αν κατά τη διαγραφή μίας κορυφής και των προσκείμενων ακμών από ένα συνδεδεμένο γράφο προκύψουν δύο ή περισσότεροι υπογράφοι, τότε η κορυφή αυτή λέγεται αποκόπτουσα κορυφή (cut-vertex) ή σημείο άρθρωσης (articulation point). Κατά τον ίδιο τρόπο, αν με τη διαγραφή μίας ακμής $e$ προκύψουν δύο συνιστώσες, τότε η ακμή αυτή ονομάζεται αποκόπτουσα ακμή (cut-edge) ή ισθμός (isthmus) ή γέφυρα (bridge). Τα τερματικά σημεία μίας τέτοιας ακμής είναι αποκόπτουσες κορυφές. Ένας γράφος χωρίς αποκόπτουσες ακμές ονομάζεται δισυναφής (bicoherent), ενώ ένας γράφος χωρίς αποκόπτουσες κορυφές ονομάζεται δισυνδεδεμένος (biconnected).

Βαθμός (degree) κορυφής λέγεται ο αριθμός των προσκείμενων ακμών. Αν ο γράφος είναι κατευθυνόμενος, τότε η έννοια του βαθμού επεκτείνεται στον έσω-βαθμό (in-degree) και στον έξω-βαθμό (out-degree) μίας κορυφής. Ο έσω-βαθμός και ο έξω-βαθμός μίας κορυφής $v$ είναι ο αριθμός των ακμών στις οποίες η κορυφή $v$ είναι κεφαλή ή ουρά αντιστοίχως.

11.2 Εσωτερική Παράσταση Γράφων

Υπάρχουν αρκετοί τρόποι απεικόνισης ενός γράφου στην κύρια μνήμη. Η αποδοτικότητα κάθε παράστασης εξαρτάται από τις συγκεκριμένες λειτουργίες που εκτελούνται στο γράφο. Στη συνέχεια, θα περιγραφούν οι τρεις συνηθέστερες μέθοδοι παράστασης γράφων: οι πίνακες διπλανών κορυφών (adjacency matrices), οι λίστες διπλανών κορυφών (adjacency lists) και οι πολλαπλές λίστες κορυφών (adjacency multilists). Στο σημείο αυτό απλώς αναφέρεται η ονομασία δύο άλλων τρόπων παράστασης: ο πίνακας προσκείμενων ακμών προς κορυφές (vertex to edge incidence matrix) και η λίστα ακμών (edge lists). Με βάση τους τρεις πρώτους τρόπους παράστασης εύκολα συμπεραίνεται η δομή των δύο τελευταίων μεθόδων.

Πίνακες Διπλανών Κορυφών

Έστω ο γράφος $G$ με $n$ κορυφές (όπου $n\geq 1$ ). Ο πίνακας διπλανών κορυφών είναι ένας τετραγωνικός πίνακας με $n\times n$ στοιχεία, που συνήθως ονομάζεται adj. Το στοιχείο adj[ $i$ , $j$ ] λαμβάνει την τιμή 1, αν η ακμή ( $v_{i},v_{j}$ ) (ή $<v_{i},v_{j}>$ για κατευθυνόμενο γράφο) ανήκει στο $Ε(G)$ , αλλιώς λαμβάνει την τιμή 0. Στο Σχήμα 11.3 φαίνονται οι πίνακες διπλανών κορυφών για τους γράφους $G_{1}$ και $G_{3}$ του Σχήματος 11.1.

Για αυτή την παράσταση των γράφων ισχύουν οι εξής παρατηρήσεις:

•

Η αποθήκευση του πίνακα αυτού απαιτεί χώρο $n^{2}$ δυαδικών ψηφίων.
•

Οι πίνακες είναι συμμετρικοί στην περίπτωση μη κατευθυνόμενων γράφων.
•

Από τον πίνακα διπλανών κορυφών είναι εύκολο να υπολογισθεί ο βαθμός κάθε κορυφής του γράφου. Συγκεκριμένα, αν ο γράφος είναι μη κατευθυνόμενος, τότε ο βαθμός του κόμβου $k$ ισούται με:

$\sum_{j=1}^{n}adj[k,j]$ (11.1)

ενώ αν ο γράφος είναι κατευθυνόμενος, τότε ο έσω- και ο έξω-βαθμός του κόμβου $k$ είναι αντιστοίχως:

$\sum_{j=1}^{n}adj[j,k]\ \ \ {\rm και}\ \ \ \sum_{j=1}^{n}adj[k,j]$ (11.2)

Ωστόσο, η υλοποίηση της μεθόδου αυτής έχει ορισμένα μειονεκτήματα:

•

Πρώτον, συχνά τίθενται ερωτήσεις της μορφής: “Πόσες ακμές έχει ο γράφος;”, “Είναι ο γράφος συνδεδεμένος;”, κλπ. Είναι φανερό ότι για να απαντηθούν τέτοιες ερωτήσεις θα πρέπει να εξετασθούν τα $n^{2}-n$ στοιχεία του πίνακα (καθώς τα στοιχεία της διαγωνίου είναι πάντοτε μηδενικά).
•

Δεύτερον, υποτίθεται ότι ο γράφος είναι στατικός, δηλαδή δεν μπορεί να γίνει ενημέρωση του γράφου με διαγραφή υπάρχοντος κόμβου ή ακμής και εισαγωγή νέου κόμβου ή ακμής.
•

Τρίτον, οι γράφοι μπορεί να είναι αραιοί με άμεση συνέπεια μεγάλη σπατάλη μνήμης.

Σε παρόμοιες περιπτώσεις εφαρμόζονται οι επόμενες δύο μέθοδοι αναπαράστασης που υπό συνθήκες μπορούν να βελτιώσουν την απόδοση των γράφων, και ως προς το χρόνο επεξεργασίας και ως προς τον απαιτούμενο χώρο αποθήκευσης.

Λίστες Διπλανών Κορυφών

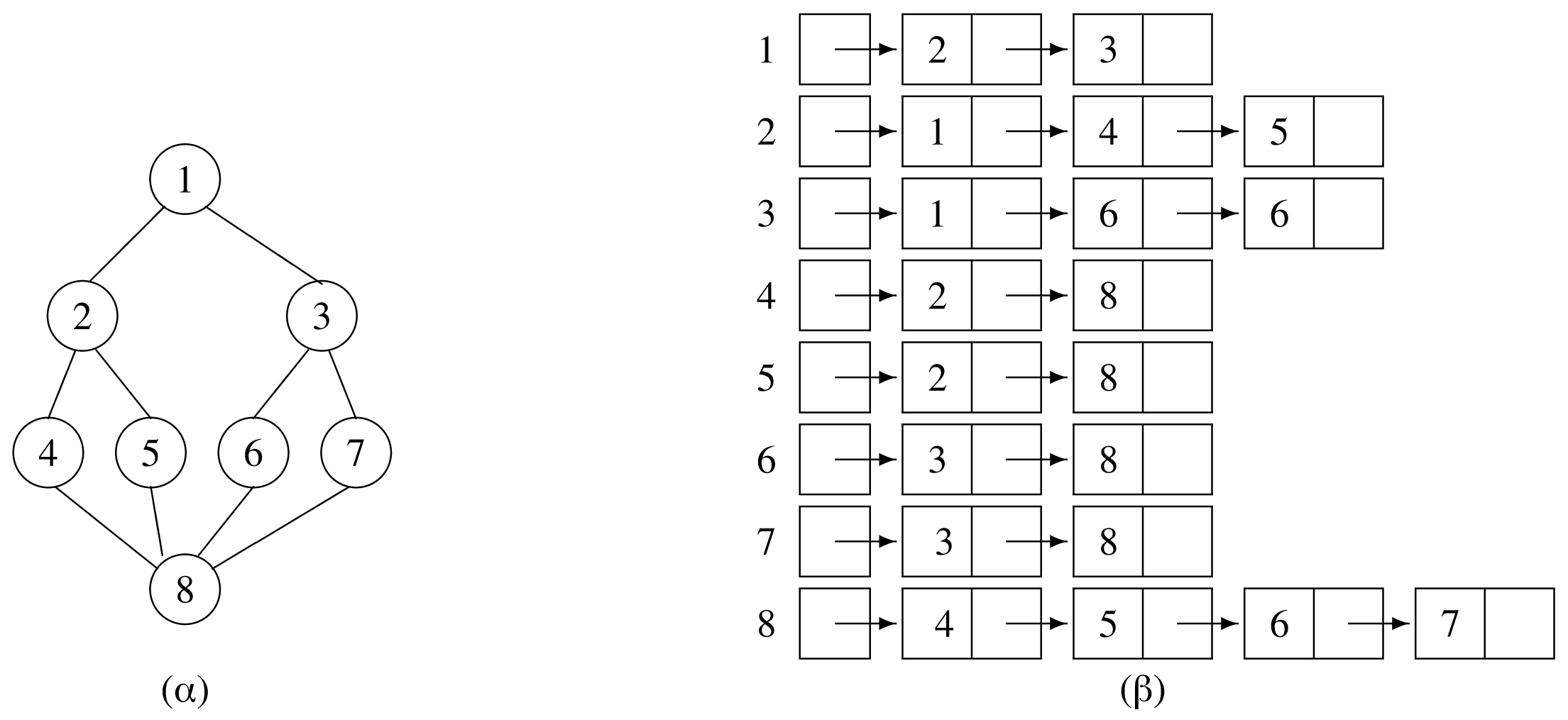
Σε αυτή την αναπαράσταση του γράφου δημιουργούνται $n$ λίστες, όπου η $i$ -οστή (για $1\leq i\leq n$ ) λίστα αντιστοιχεί στην $i$ -οστή κορυφή του γράφου και αποτελείται από μία “κεφαλή” (headnode) από όπου εξαρτώνται κόμβοι (nodes) που αντιστοιχούν στις διπλανές κορυφές της $i$ -οστής κορυφής του γράφου. Στο Σχήμα 11.4 φαίνονται οι λίστες διπλανών κορυφών για τους γράφους $G_{1}$ και $G_{3}$ του Σχήματος 11.1. Στη γενική περίπτωση, για ένα μη κατευθυνόμενο γράφο με $n$ κορυφές και $e$ ακμές απαιτούνται $n$ headnodes και $2\times e$ nodes.

Πολλαπλές Λίστες Διπλανών Κορυφών

Στην προηγούμενη εσωτερική παράσταση ενός μη κατευθυνόμενου γράφου κάθε ακμή ( $v_{i},v_{j}$ ) απεικονίζεται ως μέλος δύο λιστών. Η πρώτη λίστα αφορά στην κορυφή $v_{i}$ , ενώ η δεύτερη λίστα αφορά στην κορυφή $v_{i}$ . Σε πολλούς αλγορίθμους είναι απαραίτητο να είναι γνωστή η δεύτερη κορυφή μίας ακμής, ώστε να “σημαδεύεται ως εξετασθείσα”. Αυτό επιτυγχάνεται χρησιμοποιώντας τη μέθοδο της πολλαπλής λίστας (multilist), που είναι ένας τύπος λιστών με κόμβους που μπορεί συγχρόνως να ανήκουν και σε άλλες λίστες. Έτσι, σύμφωνα με τη μέθοδο αυτή, για κάθε ακμή θα υπάρχει ακριβώς ένας κόμβος, αλλά ο κόμβος αυτός θα συμμετέχει σε δύο λίστες.

Στο Σχήμα 11.5α παρουσιάζεται γραφικά η δομή του κόμβου πολλαπλών λιστών. Η λογική μεταβλητή $m$ δηλώνει αν η ακμή εξετάσθηκε ή όχι. Στο Σχήμα 11.5β παρουσιάζεται ο τρόπος αποθήκευσης του γράφου $G_{1}$ του Σχήματος 11.1, κάνοντας χρήση πολλαπλών λιστών. Οι μεταβλητές $N_{1}$ ως $N_{6}$ συμβολίζουν τις διευθύνσεις των εγγραφών των ακμών. Η χωρητικότητα σε μνήμη που απαιτεί η πολλαπλή λίστα διπλανών κορυφών είναι η ίδια με τη χωρητικότητα της απλής λίστας εκτός από το χώρο που απαιτείται για την αποθήκευση του $m$ .

Σχήμα 11.5: Πολλαπλή λίστα διπλανών κορυφών.

Είναι φανερό ότι όλες οι εξετασθείσες υλοποιήσεις γράφων μπορούν να επεκταθούν εύκολα ώστε να παριστάνουν ζυγισμένους γράφους. Στη μέθοδο των πινάκων διπλανών κορυφών ο δισδιάστατος πίνακας adj δεν θα περιέχει στοιχεία τύπου boolean αλλά τύπου real (για την αποθήκευση των βαρών), ενώ στις άλλες δύο μεθόδους αρκεί η προσθήκη ενός επιπλέον ειδικού πεδίου στον ορισμό του τύπου της εγγραφής.

11.3 Μέθοδοι Διάσχισης

Το πρόβλημα της διάσχισης ενός γράφου ορίζεται ως εξής. Δοθέντος ενός μη κατευθυνόμενου γράφου $G=(V,E)$ και μίας κορυφής $v\in V(G)$ , ζητείται η επίσκεψη όλων των κορυφών του $G$ ξεκινώντας από την κορυφή $v$ . Στα επόμενα δύο υποκεφάλαια θα περιγραφούν οι εξής δύο μέθοδοι διάσχισης: η αναζήτηση κατά βάθος (depth first search) και η αναζήτηση κατά πλάτος (breadth first search).

Αναζήτηση κατά Βάθος

Σύμφωνα με τη μέθοδος αυτή η αναζήτηση αρχίζει από την κορυφή $v$ , που μαρκάρεται “ως επισκεφθείσα”. Το ίδιο συμβαίνει με κάθε επισκεπτόμενη κορυφή, ώστε να αποφευχθεί μία μελλοντική επίσκεψη. Κατόπιν επιλέγεται μία κορυφή $w$ που είναι διαδοχική της κορυφής $v$ , αλλά δεν έχει ήδη επιλεχθεί. Από την κορυφή $w$ αρχίζει και πάλι μία αναζήτηση κατά βάθος. Όταν έχουν επιλεχθεί όλες οι διαδοχικές κορυφές μίας κορυφής $u$ με τη μέθοδο αυτή, τότε η αναζήτηση κατά βάθος συνεχίζεται από την προηγούμενη κορυφή της $u$ με κορυφές όπου δεν έγινε ακόμη επίσκεψη. Η αναζήτηση τελειώνει, όταν ή όλες οι κορυφές έχουν ελεγχθεί ή υπάρχουν μη ελεγχθείσες κορυφές που όμως είναι αδύνατο να προσπελασθούν από τις ήδη ελεγχθείσες. Η μέθοδος αυτή ανήκει στην οικογένεια των αλγορίθμων που βασίζονται στην οπισθοδρόμηση (δες Κεφάλαιο 6).

Στη συνέχεια, παρουσιάζεται η αναδρομική διαδικασία DFS, που καλείται με την εντολή DFS(v). Ως προς την αναπαράσταση υποτίθεται ότι ο γράφος είναι αποθηκευμένος με τη μορφή λίστας διπλανών κορυφών. Πιο συγκεκριμένα, η δομή graph είναι ένας πίνακας αποτελούμενος από κόμβους (headnodes), όπου κάθε κόμβος αποτελείται από το πεδίο mark για τη δήλωση ή μη της επίσκεψης και το πεδίο adjlist που δείχνει προς τις γειτονικές κορυφές.

procedure DFS(thisnode);
graph[thisnode].mark <-- 1;
adjptr <-- graph[thisnode].adjlist;
while adjptr<>nil do
   nextnode <-- adjptr^.node;
   if graph[nextnode].mark=0 then DFS(nextnode)
   adjptr <-- adjptr^.next

Για παράδειγμα, στο Σχήμα 11.6 παρουσιάζεται ένας μη κατευθυνόμενος γράφος με $n=8$ κορυφές και η αντίστοιχη αναπαράσταση με λίστες διπλανών κορυφών. Αν η αναζήτηση αρχίζει από την κορυφή 1, τότε η σειρά επίσκεψης των κορυφών με βάση τη διάσχιση κατά βάθος είναι 1, 2, 4, 8, 5, 6, 3 και 7.

Σχήμα 11.6: Μη κατευθυνόμενος γράφος και λίστα διπλανών κορυφών.

Αναζήτηση κατά Πλάτος

Και αυτή η μέθοδος αρχίζει από μία κορυφή που σημειώνεται “ως επισκεφθείσα”. Η αναζήτηση αυτή διαφέρει από την αναζήτηση κατά βάθος κατά ότι οι κορυφές ελέγχονται πρώτα κατά την οριζόντια κατεύθυνση αντί κατά την κατακόρυφη. Η ακόλουθη διαδικασία BFS υλοποιεί τον αλγόριθμο αναζήτησης κατά πλάτος. Η διαδικασία αυτή κάνει χρήση μίας ουράς (queue) και των αντίστοιχων διαδικασιών εισαγωγής Enqueue και εξαγωγής Dequeue. H διαδικασία θα μπορούσε να κληθεί με την εντολή BFS(v).

procedure BFS(firstnode)
graph[firstnode].mark <-- 1; Enqueue(firstnode)
while queue.front<>0 do
   Dequeue(savenode); adjptr <-- graph[savenode].adjlist;
   while adjptr<>nil do
      savenode <-- adjptr^.node;
      if graph[savenode].mark=0 then
         Enqueue(savenode); graph[savenode].mark <-- 1
      adjptr <-- adjptr.next

Για παράδειγμα, αν στο γράφο του Σχήματος 11.6 αρχικά επιλεγεί η κορυφή 1, τότε η σειρά επίσκεψης των κορυφών με βάση τη μέθοδο διάσχισης κατά πλάτος είναι 1, 2, 3, 4, 5, 6, 7 και 8.

Όσον αφορά στην επίδοση των δύο διαδικασιών ισχύουν οι εξής παρατηρήσεις:

•

Στη διάσχιση κατά πλάτος κάθε κορυφή εισέρχεται στην ουρά μόνο μία φορά. Άρα, ο εξωτερικός βρόγχος WHILE θα εκτελεσθεί $n$ φορές. Αν ο γράφος είναι αποθηκευμένος ως λίστα, τότε θα εξετασθούν μόνο οι κορυφές που είναι διπλανές στην πρώτη κορυφή. Έτσι, ο εσωτερικός βρόγχος WHILE θα εκτελεσθεί $e$ φορές και, επομένως, o συνολικός χρόνος εκτέλεσης είναι τάξης Ο( $n e$ ).
•

Αν ο γράφος είναι αποθηκευμένος ως πίνακας, τότε ο εσωτερικός βρόγχος θα εκτελεσθεί $n$ φορές. Συνεπώς, τελικά ο χρόνος εκτέλεσης της διάσχισης είναι Ο( $n^{2}$ ).
•

Με την ίδια λογική αποδεικνύεται ότι για τη διάσχιση κατά βάθος οι χρόνοι εκτέλεσης είναι ίδιοι και ανεξάρτητοι από τη μέθοδο αποθήκευσης.

11.4 Τοπολογική Ταξινόμηση

Στην τοπολογική ταξινόμηση (topological sorting) επιδιώκεται η μερική διάταξη (partial ordering) ενός συνόλου στοιχείων, δηλαδή μία διάταξη που αναφέρεται σε μερικά ζεύγη στοιχείων και όχι στην ολική διάταξη των στοιχείων, όπως απαιτεί η γνωστή μας ταξινόμησης που θα εξετασθεί στο Κεφάλαιο 8. Οι πρακτικές εφαρμογές της τοπολογικής ταξινόμησης είναι πολλές. Για παράδειγμα, σε ένα πρόγραμμα σπουδών κάποιο μάθημα χ (λόγου χάριν, οι Βάσεις Δεδομένων) μπορεί να έχει ως προαπαιτούμενο ένα άλλο μάθημα ψ (όπως τις Δομές Δεδομένων). Η σχέση αυτή συμβολίζεται με ψ $<$ χ. Η διαδικασία της τοπολογικής ταξινόμησης εξασφαλίζει τη διάταξη των μαθημάτων, έτσι ώστε να μην εμφανίζεται προς το τέλος της διάταξης κάποιο μάθημα που είναι προαπαιτούμενο κάποιου άλλου μαθήματος που έχει ήδη εμφανισθεί στη διάταξη. Επίσης, μία άλλη εφαρμογή παρουσιάζεται κατά την εκτέλεση ενός έργου, όπου είναι συνηθισμένο φαινόμενο οι διάφορες λειτουργίες να χωρίζονται σε υπολειτουργίες. Αν, λοιπόν, η υπολειτουργία $u$ πρέπει να εκτελεσθεί πριν από τις υπολειτουργίες $w$ και $z$ , τότε ισχύουν οι σχέσεις $u<w$ και $u<z$ .

Ορισμός.
Δοθέντος ενός συνόλου $S$ , μία μερική διάταξη των στοιχείων του $S$ εκφράζεται με το σύμβολο “ $<$ ” που διαβάζεται “προηγείται”. Σε μία μερική διάταξη ικανοποιούνται οι ακόλουθες τρεις ιδιότητες για κάθε διακεκριμένο στοιχείο $x, y$ και $z$ του $S$ :

Μεταβατική ιδιότητα: : Αν $x<y$ και $y<z$ , τότε ισχύει $x<z$ ,
Αντισυμμετρική ιδιότητα: : Αν $x<y$ , τότε δεν ισχύει $y<x$ ,
Αντιανακλαστική ιδιότητα: : Δεν ισχύει $x<x$ . $\Box$

Η έννοια της μερικής διάταξης μπορεί να γίνει καλύτερα κατανοητή αν θεωρηθεί η δομή του dag, του κατευθυνόμενου γράφου χωρίς κύκλους. Είναι δυνατόν το dag ως δομή να τοποθετηθεί στο ενδιάμεσο μεταξύ των γενικών κατευθυνόμενων γράφων και των δένδρων. Ο λόγος είναι ότι αν θεωρηθεί από μία κορυφή πράγματι μοιάζει με δένδρο επειδή δεν έχει ακμές με κατεύθυνση προς τα επάνω. Στο επάνω μέρος του Σχήματος 11.7 παρουσιάζεται ένα dag, ενώ στο κάτω μέρος του σχήματος παρουσιάζεται η ίδια δομή σαν δένδρο.

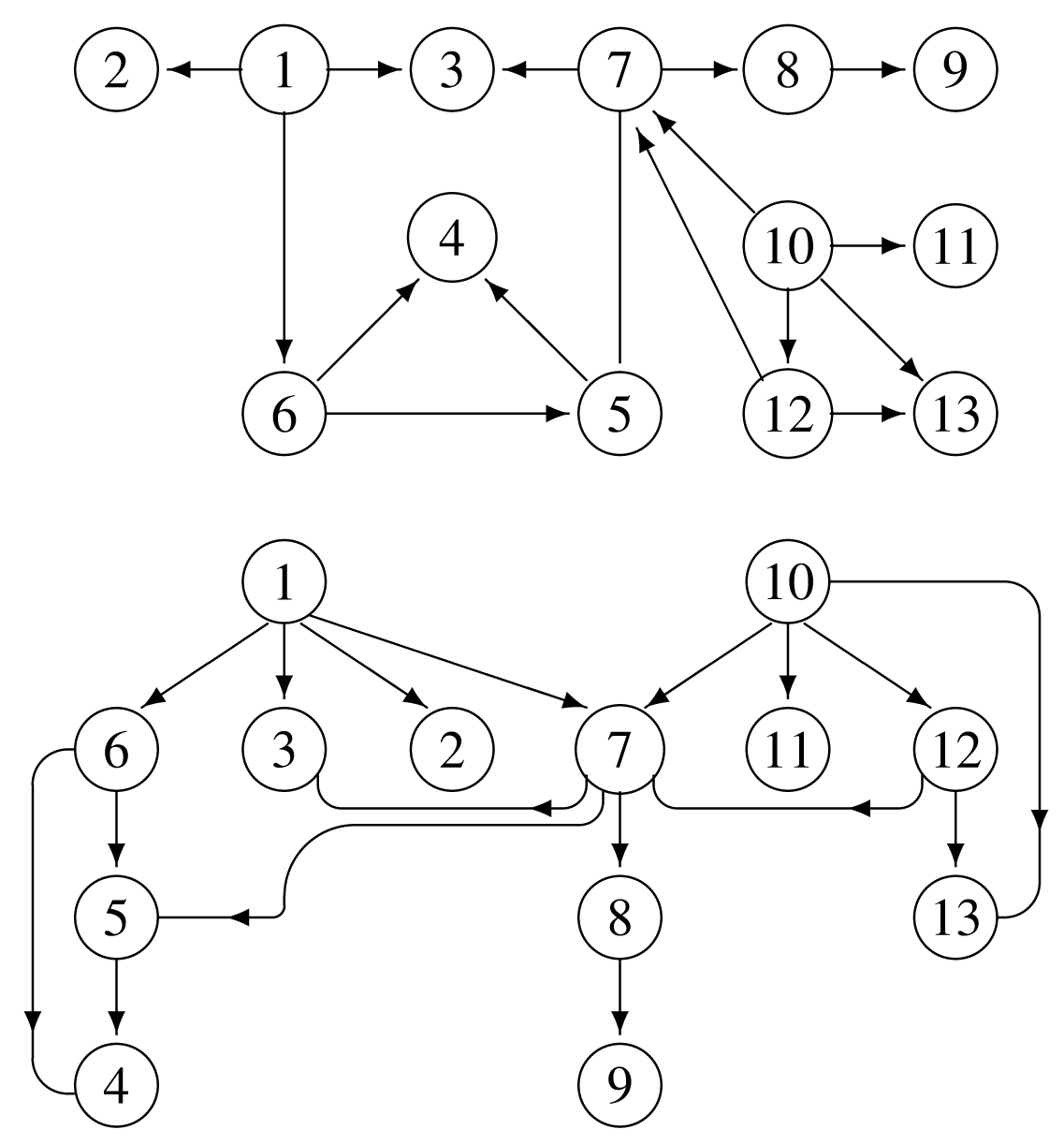
Οι δύο πρώτες ιδιότητες του ορισμού της μερικής διάταξης εξασφαλίζουν ότι ο γράφος δεν έχει κύκλους, μία αναγκαία συνθήκη για να πετύχει η τοπολογική ταξινόμηση. Ο γράφος του Σχήματος 11.7, έχει κορυφές τα στοιχεία του συνόλου $S$ , ενώ οι κατευθυνόμενες ακμές αντιστοιχούν στις συσχετίσεις. Το πρόβλημα της τοπολογικής ταξινόμησης είναι η ενσωμάτωση μίας μερικής διάταξης σε μία γραμμική διάταξη. Αυτό γραφικά φαίνεται στο Σχήμα 11.8 με την τοποθέτηση των κορυφών του γράφου στη σειρά, έτσι ώστε όλα τα βέλη να δείχνουν προς τα δεξιά. Η γραμμική αυτή διάταξη δεν είναι μοναδική, αλλά μπορεί να υπάρξουν πολλές ισοδύναμες λύσεις, όπως για παράδειγμα φαίνεται στο Σχήμα 11.8.

Σχήμα 11.8: Εναλλακτικές γραμμικές διατάξεις.

Η διαδικασία της τοπολογικής ταξινόμησης αρχίζει με κάποια κορυφή που προηγείται όλων των άλλων. Είναι φυσικό να υπάρχει τουλάχιστον μία τέτοια κορυφή γιατί αλλιώς θα υπήρχε κύκλος στον γράφο. Η κορυφή αυτή γίνεται το πρώτο στοιχείο της τελικής λίστας $L$ και συγχρόνως παύει να αποτελεί μέλος του συνόλου $S$ . Ο γράφος που απομένει εξακολουθεί να είναι μερικά διατεταγμένο κάτι που επιτρέπει την εφαρμογή της ίδιας διαδικασίας μέχρι το σύνολο $S$ να μείνει κενό. Η επόμενη διαδικασία TopologicalSort παρουσιάζει αυτό το σκεπτικό. Με το σύνολο $Q$ αποτελείται από τις κορυφές που έχουν μηδενικό έσω-βαθμό και ας υποτεθεί προς το παρόν ότι υλοποιείται με μία ουρά.

Procedure TopologicalSort;
L <-- Initialize output list
Q <-- Set of all nodes with no incoming edges
while Q is non-empty do
    remove a node n from Q
    insert n into L
    for each node m with an edge e from n to m do
        remove edge e from the graph
        if m has no other incoming edges then
            insert m into Q
if graph has edges then
    output error message (graph has a cycle)
else
    output message (proposed topologically sorted order: L)

Είναι εύκολο να αποδειχθεί η επόμενη πρόταση.

Πρόταση.
Η διαδικασία TopologicalSort απαιτεί γραμμικό χρόνο Ο( $n+e$ ). $\Box$

Η τοπολογική ταξινόμηση δεν έχει απαραιτήτως μοναδική λύση. Αν το σύνολο $Q$ υλοποιηθεί με μία στοίβα ή με ένα απλό σύνολο, τότε προφανώς το αποτέλεσμα θα είναι διαφορετικό.

11.5 Βιβλιογραφική Συζήτηση

Ο αλγόριθμος τοπολογικής ταξινόμησης προτάθηκε στο άρθρο [85]. Εκτός από τον αλγόριθμο αυτό, υπάρχει και μία άλλη μέθοδος τοπολογικής ταξινόμησης που στηρίζεται στη διάσχιση κατά βάθος [19, 34, 99].

11.6 Ασκήσεις

1.

Να σχεδιασθούν οι αλγόριθμοι διάσχισης γράφων (DFS και BFS) θεωρώντας ότι ο γράφος είναι αποθηκευμένος με τη μορφή ενός πίνακα διπλανών κορυφών ή μίας πολλαπλής λίστας. Να αναλυθούν οι διαδικασίες.
2.

Να δοθούν ικανές και αναγκαίες συνθήκες, έτσι ώστε ένα άκυκλο κατευθυνόμενο γράφημα να έχει μόνο μία πιθανή τοπολογική ταξινόμηση σε σχέση με τη σειρά που εμφανίζονται οι κορυφές.
3.

Να αποδείξετε ότι οι αλγόριθμοι DFS και BFS σε ένα συνεκτικό γράφημα $G$ παράγουν ακριβώς το ίδιο δένδρο, αν και μόνο αν το $G$ είναι δένδρο.
4.

Σχεδιάστε αλγόριθμο που να αποφασίζει αν ένα δοθεν μη κατευθυνόμενο γράφημα $G=(V,E)$ έχει κύκλο ή όχι. Ο αλγόριθμός σας θα πρέπει να έχει χρόνο εκτέλεσης $O(|V|)$ (προσοχή δεν εξαρτάται από το πλήθος των ακμών $|E|$ ).
5.

Αλλάξτε κατάλληλα τον αλγόριθμο BFS, ώστε σε κάθε κορυφή $v$ του γραφήματος $G$ να μην υπολογίζει μόνο την απόσταση από τον αρχικό κόμβο $s$ αλλά και το πλήθος των διαφορετικών μονοπατιών αυτού του μήκους.
6.

Δοθέντος ενός κατευθυνόμενου γραφήματος $G$ να περιγράψετε αλγορίθμους που να υπολογίζουν τον έξω-βαθμό κάθε κόμβου του $G$ υποθέτοντας ότι η αναπαράστασή του γίνεται με: α) λίστα διπλανών κορυφών και β) πίνακα διπλανών κορυφών. Να αναλύσετε την πολυπλοκότητα των αλγορίθμων και στις δύο περιπτώσεις.
7.

Ένα διμερές γράφημα $G=(V,E)$ είναι ένα γράφημα του οποίου το σύνολο των κορυφών $V$ μπορεί να διαμερισθεί σε δύο σύνολα $V_{1}$ και $V_{2}$ όπου $V_{1}\cup V_{2}=V$ και $V_{1}\cap V_{2}=\emptyset$ και έτσι ώστε για κάθε ακμή $(u,v)\in E$ θα ισχύει $u\in V_{1}$ και $v\in V_{2}$ ή $u\in V_{2}$ Κ και $v\in V_{1}$ . α)Αποδείξτε ότι ένα γράφημα $G$ είναι διμερές, αν και μόνο αν δεν περιέχει κύκλο περιττού μήκους. β) Δώστε έναν αλγόριθμο που χρησιμοποιεί BFS για να αποφασίσει αν ένα συνεκτικό γράφημα $G=(V,E)$ είναι ή όχι διμερές. Να αποδείξετε την ορθότητα του αλγορίθμου σας και να δείξετε την πολυπλοκότητά του.
8.

Η απόσταση μεταξύ δύο κορυφών σε ένα γράφημα είναι το μήκος του συντομότερου μονοπατιού που τα συνδέει. Η διάμετρος ενός συνεκτικού γραφήματος $G$ είναι η μέγιστη απόσταση ανάμεσα σε όλα τα δυνατά ζεύγη κορυφών του $G$ . Το ύψος ενός δένδρο με ρίζα είναι το μήκος του μακρύτερου μονοπατιού από τη ρίζα προς ένα φύλλο. Σας ζητούνται τα εξής: α) Περιγράψτε έναν αλγόριθμο πολυπλοκότητας $O(mn)$ που δοθέντος ενός συνεκτικού γραφήματος $G=(V,E)$ να βρίσκει τη διάμετρό του. β) Αποδείξτε αν ισχύει ή όχι η εξής πρόταση: Υπάρχει ένα συνεκτικό γράφημα του οποίου η διάμετρος είναι $10$ και το ύψος του BFS δένδρου είναι $4$ . γ) Δοθέντος ενός συνεκτικού γραφήματος $G=(V,E)$ να αποδείξετε ότι για κάθε κορυφή $s\in V$ το ύψος του DFS δένδρου, όταν ξεκινά από την κορυφή $s$ , είναι πάντοτε μεγαλύτερο ή ίσο με το ύψος του BFS δένδρου όταν αυτό ξεκινά από την κορυφή $s$ .
9.

Έστω ένα άκυκλο κατευθυνόμενο γράφημα $G=(V,E)$ με βάρη στις ακμές. Δώστε έναν $O(|V|+|E|)$ αλγόριθμο για την εύρεση του βάρους του μονοπατιού με το μέγιστο βάρος στο γράφημα $G$ .